Eşdeğer Sürekli Ses Düzeyi

Leq
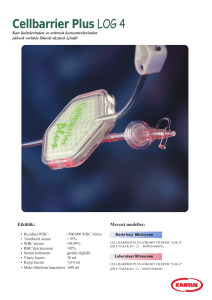
1
10 log 
T
T

0
P 2 (t ) 
dt 
2
P0

T : Ölçüm süresi
 P(t): Ölçülen sesin a ağırlık ses basıncı
 P0 : Referans ses basıncı
 dt : Ses düzeyi


Eşdeğer sürekli ses düzeyini yeterli bilgiyi sağlayamadığı bir
durum çok kısa sürer. Aniden yükseldikten sonra alçalan
seslerin değerlendirilmesidir. (Uçak havalanması) Bu tür
seslerin düzeylerini belirlemede en yaygın yöntem eşdeğer
sürekli ses düzeyini veya en yüksek ses düzeyini kullanmak
yerine ses etkileşim düzeyi (SEL)ni kullanmaktır. SEL, kısa
sürede önemli düzey değişimi gösteren bir sesin enerjisine
sahip 1 sn süren sabit düzeyli sesin düzeyidir.
Leq  SEL  10 log T
T  geçen süre
Değişik ses etkileşim düzeyi değerlerindeki n ayrı sesin
toplam T süresindeki eşdeğer sürekli ses düzeyi
aşağıdaki formülden belirlenir.
Leq
 n
SELi /10 
10 log  10
 10 log T
 i 1


Örnek: Bir noktada ölçülen ses basıncı
düzeyi değerleri; L  80 dB ,L  86 dB ,LP  85 dB
, LP  88 dB ’dir. Ortalama basınç düzeyini
hesaplayınız.
P1
P2
3
4
LPt 10 log
1
(1080 /10  1086 /10  1085 /10  1088 /10 )  85, 6 dB
4

Örnek: Her bir operasyonda çıkardığı gürültünün
ses etkileşim düzeyi SEL=110 dB olan bir makinada
çalışan bir işçi makinayı 1 günde 200 operasyon için
kullanıyor. 8 saatlik süreye karşılık gelen eşdeğer
sürekli ses düzeyini bulunuz.
Leq
 200

10 log  10 SELi /10  10 log (8  3600)
 i 1

Leq 10 log(200 10110/10 ) 10 log (8  3600)
Leq  133  44, 6  88, 4 dB

Örnek: İşlek bir cadde kenarında görev yapan bir
kişinin etkisi altında kaldığı gürültü düzeyini
saptayabilmek için yapılan çalışmalar söz konusu
noktada 8 saatte SEL değeri 96 dB olan 100
motosiklet, SEL değeri 84 dB olan 500 otobüs ve SEL
değeri 82 dB olan 15000 araba geçtiği görülmüştür.
8 saatlik süreye karşılık gelen eşdeğer sürekli ses
düzeyini bulunuz.
Leq 10 log(100 1096/10  500 1084/10  15000 1082/10 ) 10 log (8  3600)  80 dB

Sesi yansıtacak hiçbir engelin bulunmadığı ve sesin
düzgün olarak yayılabildiği alanlara serbest alan adı
verilir. Uygulamada sesin düzgün yayılmasını
önlemeyecek şekilde engellerin bulunduğu alanlar
da serbest alan olarak kabul edilir. Serbest alanda
yayılan ses dalgaları düzgündür. Ve kaynaktan r
uzaklığında olan bir noktadaki ses şiddeti r2 ile ters
orantılıdır. Serbest alanda ses gücü düzeyinden ses
basıncı düzeyi aşağıdaki şekilde hesaplanabilir.
LP  LW  10 log (
Q
)
4 r 2
LP
: Kaynaktan r uzaklıktaki ses
basıncı düzeyi
LW
: Kaynağın ses gücü düzeyi
Q
: Yönelme katsayısı
r
: Mesafe (m)

Kaynağa olan uzaklık her 2 katına çıktığında ses düzeyinde
azalma 6 dB, her 10 katına çıktığında 20 dB’dir.



Nokta kaynakların ardarda bir doğrultuda olması ile çizgi
kaynaklar oluşur. Çizgi kaynaklarda uzaklık her 2 katına
çıktığında ses düzeyindeki azalma 3 dB, her 10 katına
çıktığında 10 dB’dir.

Hava molekülleri, ses dalgalar halinde yayılırken ses enerjisinin bir kısmını
yutar. Özellikle uzak mesafelerde bu yutuş miktarının dikkate alınması
gereklidir. Atmosferik yutuş 20 ºC için aşağıdaki şekilde hesaplanır:

Aatm
f
r
2

f
r
8
 7, 4 10 

 Ø 
: İletilen sesin frekansı (Hz)
: Kaynaktan olan uzaklık (m)
Aatm
: Atmosferik yutuş ile ses
basıncındaki düşüş (dB)
Ø
: Havanın bağıl nemi (%)

Örnek: Ses gücü düzeyi, LW = 130 dB olan bir itfaiye
sireninin 4000 Hz frekansında yaydığı sesin açık
havada r = 500 m uzaklıkta oluşturacağı ses basıncı
düzeyini bulunuz. (Ø
= %50, T = 20 ºC, Q = 1)
Aatm  7, 4 10
8
 40002  500 

 12 dB
50


LP  LW  10 log (
LP  130  10 log (
1
4   500 
2
Q
)
2
4 r
)  65 dB
Toplam azalma = 65–12 = 53 dB

Örnek: 500 ile 100 hz arasındaki 4 oktav bandındaki
ses gücü düzeyi 88 dB olan bir makinanın açık
havada makinadan 3 m uzaklıktaki bir noktada ses
basıncı düzeyini bulunuz. (Q=2)
LP  LW
Q
 10 log (
)
2
4 r
LP  88  10 log
2
 70, 5 dB
4  9

Örnek: Bir makinanın ses gücü düzeyi 500, 1000,
2000 ve 4000 hz oktav bantlarında sırasıyla , , , ’dir.
Bu makinadan 3 m uzaklıktaki ses basıncı düzeyini
bulunuz. (Q = 2)
LP  LW  10 log (
LP  LW  10 log
Q
)
2
4 r
2
4  9
LP  LW  17, 5
Merkez frekans(Hz)
LW (dB)
LP (dB)
500
74
56,5
1000
86
68,5
2000
82
64,5
4000
76
58,5
LP 10 log(1056,5/10  1068,5/10  1064,5/10  1058,5/10 )  70,5 dB

Bu denklem sadece arı seslerin yani tek bir frekansa
sahip seslerin ses yüksekliklerini belirlemede kullanılır.
Karmaşık seslerin yükseklik düzeyleri ölçülmek
istendiğinde Şekil 2.4’te verilen eş yükseklik indeksi
eğrileri kullanılır. Bu yöntemde öncelikle her oktav
bandındaki bant basıncı düzeyleri (BBD) ölçülür.
Genellikle 63, 125, 250, 500, 1000, 2000, 4000, 8000 Hz
bantlarının kullanılması yeterlidir. Daha sonra her merkez
frekansı ve buna karşılık gelen BBD kullanılarak her
battaki yükseklik indeksi Şekil 2.4’ten bulunur. Son olarak
toplam ses yüksekliği aşağıdaki formülden belirlenir.
St  S m
St
Si
Sm
K
 n

 K   Si  S m 
 i 1

: Toplam ses yüksekliği (son)
: i ses yüksekliği indeksi
: En büyük yükseklik indeksi
: 0,3 (sabit)



Toplam ses yüksekliği kullanılarak ses yüksekliği düzeyi de
belirlenebilir. Kapalı yerlerdeki arka plan gürültüsünün düzeyini
saptamanın ve bilinen sınır değerler ile kıyaslamanın en bilinen
yolu, gürültü ölçütü (NC) eğrilerini kullanmaktır. (Şekil 2.5)
Her eğri, verilen belli bir NC değeri için ulaşılabilecek en yüksek
oktav bant basıncı düzeyini göstermektedir. İncelenen
gürültünün ölçülen bant basıncı düzeyleri NC eğrileri üzerinde
işaretlenir. En büyük NC değerine yakın nokta gürültünün NC
değerini verir. Bu NC eğrileri zamanla geliştirilerek tercih edilir.
Genellikle bir ses kaynağından çıkan ses dalgaları, her
yönde farklı yayılır. Bir noktadaki yönelme katsayısı (Q), o
noktadaki ses şiddetinin sesin düzgün yayılması
durumunda aynı noktada oluşturacağı ses şiddetine
oranı olarak tanımlanır.
I
Q 
It
 Çevresinde hiçbir yansıtıcı yüzey bulunmayan noktasal
bir cisim, her yönde değişik yönelme katsayısına sahip
bir ses kaynağının herhangi bir yöndeki yönelme
katsayısı, o yönde bir noktada ölçülen ses basıncı düzeyi
kullanılarak aşağıdaki şekilde belirlenir


.
Q  10
( L p  L p ) /10

Örnek: Bir ses kaynağının 4 m uzaklığında ortalama
ses basıncı düzeyini hesaplamak için 8 uygun
noktada ölçümler yapılmıştır. Yönelmenin en fazla
olduğu yönü ve yönelme katsayısını bulunuz.
LP1  88 dB
LP2  90 dB
LP6  96 dB
LP3  87 dB
LP7  92 dB
LP4  92 dB
LP5  99 dB
LP8  86 dB
1
LP 10 log (1088/10  1090/10  1089/10  1092/10  1099/10  1096/10  1092/10  1086/10 )  93, 4 dB
8