5.SINIF MATEMATİK ÜNİTE -1
ÇOKGENLER-1
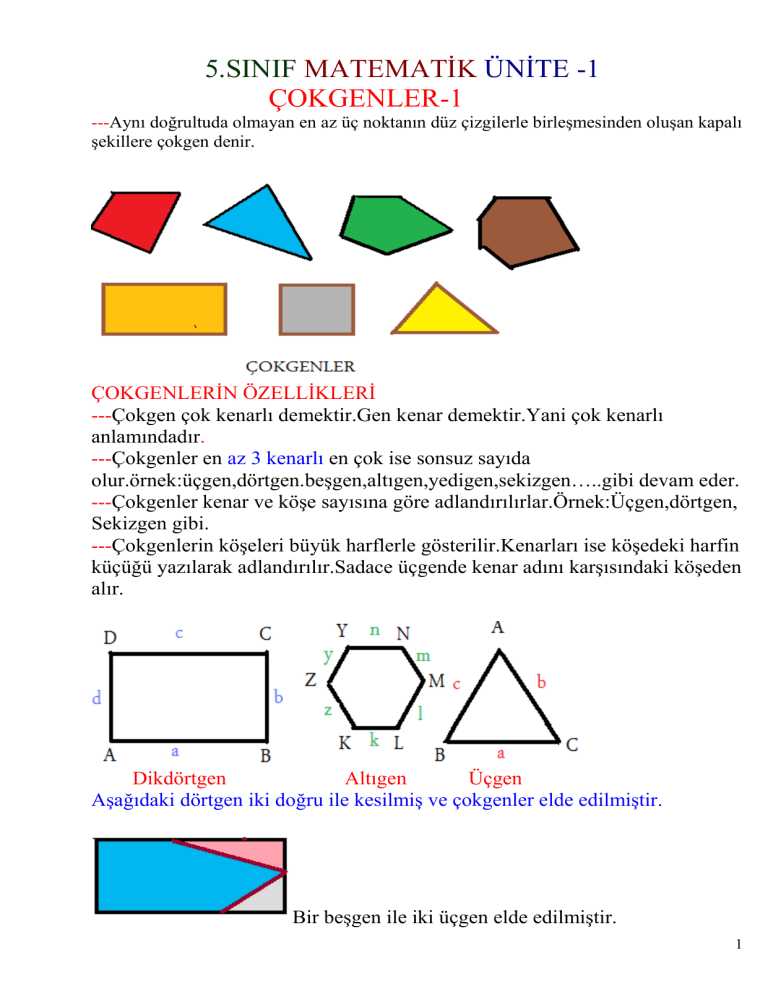
---Aynı doğrultuda olmayan en az üç noktanın düz çizgilerle birleşmesinden oluşan kapalı
şekillere çokgen denir.
ÇOKGENLERİN ÖZELLİKLERİ
---Çokgen çok kenarlı demektir.Gen kenar demektir.Yani çok kenarlı
anlamındadır.
---Çokgenler en az 3 kenarlı en çok ise sonsuz sayıda
olur.örnek:üçgen,dörtgen.beşgen,altıgen,yedigen,sekizgen…..gibi devam eder.
---Çokgenler kenar ve köşe sayısına göre adlandırılırlar.Örnek:Üçgen,dörtgen,
Sekizgen gibi.
---Çokgenlerin köşeleri büyük harflerle gösterilir.Kenarları ise köşedeki harfin
küçüğü yazılarak adlandırılır.Sadace üçgende kenar adını karşısındaki köşeden
alır.
Dikdörtgen
Altıgen
Üçgen
Aşağıdaki dörtgen iki doğru ile kesilmiş ve çokgenler elde edilmiştir.
Bir beşgen ile iki üçgen elde edilmiştir.
1
DÜZGÜN ÇOKGEN:Açılarının ölçüleri ile kenarlarının ölçüleri eşit olan
Çokgenlere düzgün çokgen denir.
Kare
üçgen
beşgen
altıgen
Düzgün dörtgen düzgün üçgen düzgün beşgen düzgün altıgen
---Kenarları ve açıları eşit olmayan çokgenler düzgün çokgen değildir.
DÖRTGENLER
---Dört köşesi olan kapalı şekillere dörtgen denir.
Köşegen:Karşılıklı köşeleri birleştiren doğru parçalarına köşegen denir.
[AC] ve [DB] birer köşegendir.
---Dörtgenlerde ikişer köşegen vardır.
EK BİLGİ:Bir çokgende köşegen sayısını bulmak için kenar sayısından 3
çıkarılarak kenar sayısı ile çarpılıp 2 ye bölünerek bulunur.
Soru:Sekizgenin kaç köşegeni vardır?
Çözüm: 8-3=5
5x8=40
40:2=20 köşegeni vardır.
---Dörtgenlerin iç açıları toplamı 360 derecedir.
---Dörtgenlerde ardışık açıların toplamı 180 derecedir.
DÖRTGEN ÇEŞİTLERİ
1-Kare
2-Dikdörtgen
2
3-Paralelkenar
4-Eşkenar dörtgen
5-Yamuk
1-KARE
A)Köşegenler
b)Simetri Eksenleri(katlama doğrusu)
3
KARENİN ÖZELLİKLERİ
---4 kenarı da birbirine dik ve eşittir.
--- 4 Açısı vardır ve dik açıdır.
---İç açıları toplamı 360 derecedir.
---Ardışık iki açısının toplamı 180 derecedir.
---Köşegenleri karenin açılarını 45 er derecelik iki eşit açıya böler.
Karenin Çevresini Hesaplama
Karenin Alanını Hesaplama 1.yol
8x8=64 birim kare alanı bulunur.
SORU:Bir kenarı 7 m olan karenin alanı ve çevresini bulunuz.
ÇÖZÜM:Ç=4x7=28 m çevresi.
A=7x7=49 m2 alanı bulunur.
4
Karenin Alanını Bulma 2.yol
---Karenin köşegen uzunlukları çarpılıp 2’ye bölünerek karenin alanı bulunur.
YÜKSEKLİK: Herhangi bir köşeden karşı kenara çizilen dik doğruya o
kenara ait yükseklik denir.Karenin 4 kenarı da birer yüksekliktir.
2-DİKDÖRTGEN
Köşegen,Açı ve Kenar Özellikleri
---Dikdörtgende bir köşegen dikdörtgeni eşit 2 ikizkenar dik üçgene ayırır
---Dikdörtgende 2 köşegen dikdörtgeni 4 ikizkenar üçgene ayırır.Ancak bu
üçgenler karşılıklı olarak birbirinin aynısıdır.
---Dikdörtgenin karşılıklı kenarları birbirine eşit ve paraleldir.
---Köşegen uzunlukları birbirine eşittir.Köşegenler birbirini ortadan keserler.
---Dikdörtgenin açıları dik açı olup iç açıları toplamı 360 derecedir.
Simetri Eksenleri
---Dikdörtgenin kenarlarının orta noktalarını birleştiren doğrular simetri
eksenleridir.2 tanedir.
5
Dikdörtgenin Çevresi
1.yol-Dikdörtgenin bir kısa kenarı ile bir uzun kenarını toplayıp 2 ile çarparak
çevresini buluruz. Ç=2x(a+b)
2.yol-Kısa kenarları ayrı uzun kenarları ayrı 2 ile çarpıp her iki çarpımı
toplayarak çevreyi buluruz.
Ç=(2xa)+(2xb)
3.yol-4 kenarını toplayarak buluruz. Ç=a+a+b+b
Dikdörtgenin Alanı
ALANI:Uzun ve kısa kenar boyunca dizilen birim karelerin sayıları çarpılarak
dikdörtgensel yüzeyi kaplayan birim karelerin sayısı bulunur.
Birim kare sayısı:8 birim kare x4 birim kare=32 birim kare
Örnekte görüldüğü gibi dikdörtgenin alanını bulmak için
ALAN=Uzun kenar x kısa kenar
ALAN=axb
Veya
ALAN=Taban x Yükseklik
şeklinde de bulunabilir.
ÖRNEK SORU:Uzun kenarı 45 m,kısa kenarı 23 m olan dikdörtgen
şeklindeki tarlanın çevresi ve alanı ne kadardır?
ÇEVRE:2x(a+b)
2x(45+23)
2x68=136 m çevresi
ALANI:axb
:23x45=1035 m2 alanı bulunur.
Not:Dikdörtgende hem uzun kenar hem de kısa kenar yükseklik olarak
kullanılabilir.
6