ÜÇGENLER
ÜÇGEN
ÜÇGENİN ÖZELLİKLERİ
ÜÇGEN ÇEŞİTLERİ
PİSAGOR BAĞINTISI
ÖKLİD BAĞINTISI
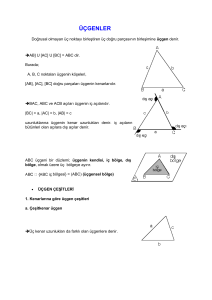
Üçgen:
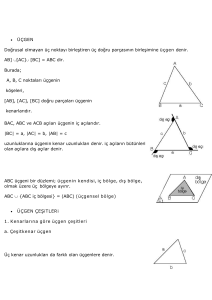
Doğrusal olmayan üç noktayı birleştiren üç doğru
parçasının birleşimine üçgen denir.
ÜÇGENİN ÖZELLİKLERİ
A
B
C
Burada;
A, B, C noktaları üçgenin
köşeleri,
[AB], [AC], [BC] doğru parçaları üçgenin
kenarlarıdır.
|BC| = a, |AC| = b, |AB| = c uzunluklarına
üçgenin kenar uzunlukları denir.
BAC, ABC ve ACB açıları üçgenin iç
açılarıdır.
İç açıların bütünleri olan açılara dış açılar
denir.
• Bir Üçgenin iç açılarının toplamı 180°; dış
açılarının toplamı 360°'dir.
• Bir üçgende, bir köşedeki iç açı ile diş açının
toplamı 180°’dir.
• Üçgende bir dış açı, kendisine komşu olmayan
iki iç açının toplamına eşittir.
ÜÇGENDE ALAN
Genel Alan Bağıntısı
• ABC üçgeninde [BC] kenarına ait yükseklik
[AH]=h ve BC kenar uzunluğu a olsun.
• Bir üçgenin alanı, bir kenarı ile o kenara ait
yüksekliğin çarpımının yarısıdır.
• Hangi kenarı kullanırsak kullanalım üçgenin
alanı sabittir. Bir ABC üçgeninde yükseklik her
zaman üçgenin içinde olmayabilir.
Alan =axhx(1/2)
h
H
ABC üçgeni bir düzlemi; üçgenin kendisi, iç
bölge, dış bölge, olmak üzere üç bölgeye ayırır.
Üçgen Çeşitleri
1.Kenarlarına Göre Üçgenler
ÇEŞİTKENAR
ÜÇGEN
İKİZKENAR
ÜÇGEN
EŞKENAR
ÜÇGEN
2.Açılarına Göre Üçgenler
DAR AÇILI
ÜÇGEN
DİK AÇILI
ÜÇGEN
GENİŞ AÇILI
ÜÇGEN
Kenarlarına Göre Üçgenler
a. Çeşitkenar üçgen
Üç kenar uzunlukları da farklı olan üçgenlere denir.
A
c
b
B
C
a
b. İkizkenar Üçgen
Herhangi iki kenar uzunlukları eşit olan
üçgenlere denir.
1.İkizkenar üçgenin tepe açısından tabanına
çizilen yükseklik, hem açıortay, hem de
kenarortaydır.
2.Bir üçgende, açıortay aynı zamanda
yükseklik ise bu üçgen ikizkenar üçgendir.
lBDl=lDCl
m(B)=m(C)
lABl=lACl
3.Bir üçgende, açıortay aynı zamanda
kenarortay ise bu üçgen ikizkenar üçgendir.
lAB=lACl
m(B)=m(C)
4.Bir üçgende, yükseklik aynı zamanda kenarortay
ise bu üçgen ikizkenar üçgendir.
lABl=lACl
m(BAH)=m(HAC)
m(B)=m(C)
5.İkizkenar üçgende, eşit kenarlara ait
kenarortay uzunlukları birbirine eşittir.
6.İkizkenar üçgende ikizkenara ait yükseklikler
eşittir. Bu durumda yüksekliklerin kesim
noktasının ayırdığı parçalar eşit olur.
7.İkizkenar üçgende ikizkenara ait
kenarortaylar ve kenarortayların kesim
noktasının ayırdığı parçalar da birbirine eşittir.
8.İkizkenar üçgende eşit açılara ait
açıortaylar da eşittir. Açıortaylar birbirini
aynı oranda bölerler.
9. İkizkenar üçgende ikiz olmayan kenar
üzerindeki herhangi bir noktadan ikiz kenarlara
çizilen dikmelerin toplamı, ikizkenarlara ait
yüksekliği verir.
lABl=ACl
lLCl=lHPl+lKPl
10.İkizkenar üçgende tabandan ikiz
kenarlara çizilen paralellerin toplamı, ikiz
kenarların uzunluğuna eşittir.
ABl=lACl
lEDl//lACl
lFDl=lABl
lABl=lACl=lED+lEFl
c. Eşkenar Üçgen
Bütün kenar uzunlukları eşit ve bütün iç açıları
60 derece olan üçgenlere ‘eşkenar üçgen’ denir.
1. Eşkenar üçgende bütün açıortay,
kenarortay yükseklikler çakışık ve hepsinin
uzunlukları eşittir.
2. Eşkenar üçgenin bir kenarına a dersek yük seklik
Bu durumda eşkenar üçgenin alanı
h
3.Eşkenar üçgenin içindeki herhangi bir noktadan
kenarlara çizilen dik uzunlukların toplamı, eşkenar
üçgene ait yüksekliği verir.
Bir kenarı a olan eşkenar üçgende;
4. Eşkenar üçgenin içindeki herhangi bir noktadan
kenarlara çizilen paralellerin toplamı bir kenar
uzunluğuna eşittir.
Bir kenarı a olan ABC eşkenar üçgeninde;
Açılarına Göre Üçgenler
a. Dar açılı üçgen
Üç açısının ölçüsü de 90° den küçük olan üçgenlere
dar açılı üçgen denir.
b. Dik açılı üçgen
Bir açısının ölçüsü 90° ye eşit olan üçgenlere
denir.
Dik üçgen olarak adlandırılır.
Dik Üçgende Alan
• Dik üçgenin alanı dik kenarlarının çarpımının
yarısına eşittir.
Alan=lABlxlAClx(1/2)
c. Geniş açılı üçgen
Bir açısının ölçüsü 90° den büyük olan üçgenlere
denir.
Bir üçgende bir tek geniş açı olabilir.
PİSAGOR BAĞINTISI
Dik üçgende dik kenarların uzunluklarının
kareleri toplamı hipotenüsün uzunluğunun
karesine eşittir.
ABC üçgeninde m(A) = 90°
a2=b2+c2
ÖKLİT BAĞINTILARI
Dik üçgenlerde hipotenüse ait yüksekliğin
verildiği durumlarda benzerlikten kaynaklanan
Öklid Bağıntıları kullanılır.
1.Yüksekliğin hipotenüste ayırdığı parçaların
çarpımı yüksekliğin karesine eşittir.
h2 = p.k
3. ABC üçgeninin alanını iki farklı şekilde
yazıp eşitlediğimizde a.h =b.c
Yukarıda anlatılan öklit bağıntıları
kullanılarak elde edilir.
Genellikle bu öklit bağıntısını kullanmak
yerine, yukarıdaki öklit bağıntıları ve
pisagor bağıntısını kullanarak çözüme
gideriz.
HAZIRLAYAN
•
•
•
•
SALİM ÖZATA
110403005
İKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ
2/A GÜNDÜZ
ZAMAN AYIRDIĞINIZ İÇİN TEŞEKKÜRLER