Slayt 1 - WordPress.com
advertisement

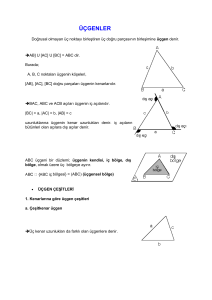
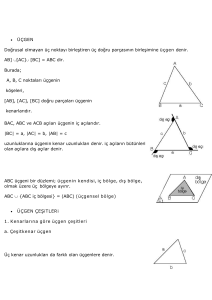
ÜÇGENLER İÇİNDEKİLER Açılarına göre üçgenler Üçgenin temel elemanları Üçgende açı ilişkileri Kenarlarına göre üçgenler Üçgende eşlik-benzerlik Kenarortay, açıortay,yükseklik Pisagor bağıntısı Kazanımlar Kaynakça Açılarına Göre Üçgenler Dar Açılı Üçgen Dik Açılı Üçgen Geniş Açılı Üçgen Kenarlarına Göre Üçgenler Eşkenar Üçgen İkizkenar Üçgen Çeşitkenar Üçgen Aynı doğru üzerinde bulunmayan üç noktanın ikişer ikişer birleştirilmesiyle elde edilen şekle üçgen denir. A C kenarı B b kenarı a kenarı C Üçgenin köşeleri: A,B,C noktaları Üçgenin kenarları: AB , BC , AC doğru parçalarıdır. A B C Üçgen bulunduğu düzlemi üç bölgeye ayırır. K L 1-Üçgenin kendisi 2-Üçgenin iç bölgesi 3-Üçgenin dış bölgesi M ÜÇGENİN TEMEL ELEMANLARI Köşeler Temel elemanlar Dış açı c B Kenarlar A İç açı İç açı Dış açı Açılar b İç açı a Dış açı C Üçgenin Açıları ^ A ^ B ^ C Üçgenin iç açıları: Üçgenin dış açıları: ^ ^ BAC= A A (A üssü açısı) ^ ^ ABC= B B (B üssü açısı) ^ ^ . BCA= C C (C üssü açısı) ÜÇGENDE AÇI İLİŞKİLERİ › Bir üçgenin iç açılarının ölçüleri toplamı 180 derecedir. A › Örnek: 80 50 › Çözüm: B › 180-(80+50) › 180-130= 50 derece ? C Açılarına Göre Üçgenler Üçgenler açılarına göre 3’e ayrılır. 1-Dar açılı üçgenler 2-Dik üçgen 3-Geniş açılı üçgen 1-Dar açılı üçgen Üç açısı da dar açı olan üçgenlerdir. A 70 60 B 50 C Yukarıdaki üçgenin açılarının tümü 90 dereceden küçük olduğu için dar açılı bir üçgendir. 2-Dik üçgen Bir açısı 90 derece olan üçgenlerdir. V Z Y 3-Geniş açılı üçgen AA C B Bir açısı 90 dereceden büyük olan üçgenlerdir. Kenarlarına Göre Üçgenler Üçgenler kenarlarına göre üçe ayrılır. 1-Eşkenar üçgen Üç kenar uzunluğu birbirine eşit olan üçgenlere eşkenar üçgen denir. A 10 cm 10 cm C B 10 cm 2-İkizkenar üçgen İki kenarı birbirine eşit olan üçgenlere ikizkenar üçgen denir. A 6 cm 6 cm B C 2 cm 3-Çeşitkenar üçgen Üç kenar uzunluğu birbirinden farklı olan üçgenlere çeşitkenar üçgen denir. D 10 cm 6 cm E F 13 cm Üçgende Eşlik ve Benzerlik Benzer Üçgenler: Karşılıklı açıları eş ve karşılıklı kenarları orantılı olan üçgenlere benzer üçgenler denir. ABC ve DEF üçgenleri için; m(A)=m(D) m(B)=m(E) a/d=b/e=c/f m(C)=m(F) Buradan ABC üçgeni ile CEF üçgeni benzerdir ve; ABC≈DEF biçiminde gösterilir. eşitliğinde verilen k sayısına,benzerlik oranı yada benzerlik katsayısı denir. k = 1 olan benzer üçgenlerde karşılıklı kenarlar eşit olduğundan, bu üçgenlere eş üçgenler denir. ABC ~ DEF benzerliği yazılırken eş açıların sıralanmasına dikkat edilir. Kenarortay,Açıortay,Yükseklik Kenarortay : Bir üçgenin bir kenarının orta noktasını karşı köşeye birleştiren doğru parçasına kenarortay denir. Kenarortayların kesiştiği noktaya ağırlık merkezi denir. G, ağırlık merkezi ise; IAGI=2IGFI ve IBGI=2IGDI ve IGCI=2IGEI olur. Açıortay: Herhangi bir açının ölçüsünü iki eş açıya bölen ışınlara açıortay denir. Yukarıdaki şekilde AOB açısını iki eş açıya ayıran [OC ışınına açıortay denir. Yükseklik::Üçgenin bir köşesinden karşı tarafa indirilen, köşe ile kenar arasında kalan doğru parçasına “Üçgenin Yüksekliği” denir. ”h” ile gösterilir. Yükseklik-Açıortay-Kenarortay Karşılaştırılması PİSAGOR BAĞINTISI Pisagor teoremine göre bir dik üçgende dik kenarların karelerinin toplamları hipotenüsün karesine eşittir. Burada hipotenüs 90 derecelik açının karşısındaki kenardır. KAZANIMLAR Terimler: Hipotenüs, Pisagor bağıntısı, üçgen eşitsizliği, dik kenarlar, kenarortay, açıortay, yükseklik Üçgende kenarortay, açıortay ve yüksekliği inşa eder. Kâğıtları katlayarak, keserek veya kareli kâğıt üzerinde çizim yaparak üçgenin elemanlarını oluşturmaya yönelik çalışmalara yer verilir. Eşkenar, ikizkenar ve dik üçgen gibi özel üçgenlerde kenarortay, açıortay ve yüksekliğin özelliklerini belirlemeye yönelik çalışmalara da yer verilir. Üçgenin iki kenar uzunluğunun toplamı veya farkı ile üçüncü kenarının uzunluğunu ilişkilendirir. Somut modeller kullanılarak yapılacak etkinliklere yer verilebilir. Uygun bilgisayar yazılımları ile üçgen eşitsizliğini anlamaya yönelik çalışmalara yer verilebilir. Üçgenin kenar uzunlukları ile bu kenarların karşısındaki açıların ölçülerini ilişkilendirir. Dik üçgende dik kenarlar ve hipotenüs tanıtılıp açı ölçüleriyle kenar uzunlukları arasındaki ilişki de ele alınır. Yeterli sayıda elemanının ölçüleri verilen bir üçgeni çizer.Üç kenarının uzunluğu, bir kenarının uzunluğu ile iki açısının ölçüsü, iki kenar uzunluğu ile bu kenarların arasındaki açının ölçüsü verilen üçgenlerin uygun araçlar kullanılarak çizilmesi sağlanır Pisagor bağıntısını oluşturur; ilgili problemleri çözer. Pisagor bağıntısının gerçek yaşam uygulamalarına yönelik çalışmalara yer verilir. Koordinat düzlemi üzerinde verilen iki nokta arasındaki uzaklığı Pisagor bağıntısını kullanarak bulma çalışmalarına yer verilir. Kenar uzunlukları verilen bir üçgenin dik üçgen olup olmadığına Pisagor bağıntısını kullanarak karar vermeye yönelik çalışmalar yapılır. KAYNAKÇA: Talim ve Terbiye Kurulu Başkanlığı Öğretim Programı Matematik(5-8) http://www.matematik.canavari.net/2013/04/kenarortaynedir.html https://www.google.com.tr/search?q=a%C3%A7%C4%B1orta y&espv=2&biw=1366&bih=624&source=lnms&tbm=isch&sa =X&ei=_Lz1VIKxHMLZarTYgrgK&sqi=2&ved=0CAYQ_AUoAQ https://www.google.com.tr/search?q=a%C3%A7%C4%B1orta y&espv=2&biw=1366&bih=624&source=lnms&tbm=isch&sa =X&ei=_Lz1VIKxHMLZarTYgrgK&sqi=2&ved=0CAYQ_AUoAQ#t bm=isch&q=kenarortay http://www.matematikvegeometri.com/8.-sinif-sbs-oku/ucgenlerde-eslik-ve-benzerlik.html