DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
YEDİNCİ BÖLÜM:TEMEL AĞ KURAMLARI
Anahtar kelimeler
İki taraflı direnç, sabit akım kaynağı, sabit gerilim kaynağı, verim, empedans, doğrusal ağ, maksimum
güç aktarım kuramı, çok kaynaklı devre, ağ, Norton kuramı, sürekli durum çalışma şartı, toplamsallık
kuramı, Thevenin kuramı.
Bu bölümde yaygın olarak başvurulan elektriki ağ kuramları tartışılacaktır. Bunlar maksimum güç
aktarım, toplumsallık, Thevenin ve Norton kuramlarıdır. Ağ kavramını elektriki olarak bağlanmış
bileşenler kümesi anlamında kullanıyoruz. Kuramlar başlangıçta çok açık olmayan ancak bazı
terimlerle ispatlanabilen durum ya da fikirlerdir. İspat sonrasında kuramlar kanun haline gelir. Bu
bölümde öğreneceğiniz kuramlar hem hesapla, hem de uygulamayla ispatlanabilmektedir. İki taraflı
direnç derken her iki yönde akan akım için de aynı gerilim düşümü ve direnç değerini gösteren direnç
anlatılmaktadır ve sürekli durum çalışma şartlarında doğrusal ağlarda kullanılan iki taraflı dirençlere
göre kuramlar anlatılacaktır.
Maksimum güç aktarım kuramını kullanarak bir kaynaktan yüke en büyük gücü aktarmak için yükün
değerinin ne olması gerektiğini belirleyebiliriz. Mesela yükselticiden hoparlörlere en büyük gücün
aktarılması için hoparlör empedansının ne olması gerektiği gibi. Toplamsallık kuramı birden fazla
kaynağa sahip devrelerin çözümlenmesini kolaylaştırmaktadır. Thevenin kuramını kullanarak devrenin
tamamını çözümlemeden diyelim ki değişik yük dirençleri için elektriki parametrelerin belirlenmesini
sağlayan bir Thevenin eşdeğer devresine sahip olabilmekteyiz. Norton kuramı da benzer olarak
karmaşık devreleri basitleştirerek çözümlemeyi kolaylaştırmaktadır.
Bu bölümde kazandırılacak yeterliklerden sonra öğrenci;
Maksimum güç aktarım kuramını açıklar.
Verilen bir devrede maksimum güç aktarımı için gereken RL değerini belirler.
Toplamsallık kuramını ifade eder.
Çok kaynaklı devreler için parametreleri hesaplar.
Thevenin kuramını ifade eder.
Verilen bir devre veya ağdaki belirtilen uçlar arasına bağlanan değişik R L değerleri için VL ve
IL’leri hesaplar.
Norton kuramını ifade eder.
Norton kuramını kullanarak istenen problemleri çözer.
Norton ve Thevenin eşdeğer parametrelerini birbirilerine dönüştürür.
Bazı önemli ifadeler
İki taraflı direnç, içinden geçen akım hangi yönde olursa olsun değeri aynı kalan dirençlerdir. Bu tür
dirençlerin uçları arasındaki gerilim düşümünün değeri de akım yönünden bağımsızdır.
Doğrusal ağ; elektriki davranışı farklı akım ve gerilim seviyeleri veya değerleri ile değişmeyen
devrelerdir.
Sürekli durum çalışma şartı; devre değerleri ve şartlarının kararlı veya sabit olduğu çalışma
durumlarıdır. Bunun tersi geçici şartlardır. Mesela bir durumdan veya seviyeden bir diğerine geçişte
değerlerin değiştiği, anahtarın açık ya da kapalı olma durumları geçici durumlardır. Ya da bir elektrik
devresinde çalışan bir motorun normal şartlardaki çalışması sürekli durum iken, bir süre için motor
milinin hesapta olmayan bir mekanik etki ile zorlanması ve buna bağlı olarak devreden o dönem için
daha fazla akım çekmesi geçici çalışma şartıdır.
MAKSİMUM GÜÇ AKTARIM KURAMI
Elektronik devrelerin bir çoğu için kaynaktan yüke en büyük değerde gücün aktarılması son derece
önemlidir. Sözgelimi radyo veya televizyon iletim sistemlerinde vericinin son aşamasından anten
sistemine mümkün olan en büyük gücün aktarılması arzu edilir. Sizin kullandığınız bir yükseltici de
hoparlör sistemine en büyük gücün aktarılmasını istersiniz. Bunu sağlamak için yükün direnci veya
empedansı ile kaynağın direnci veya empedansının eşleşmesi gerekir. Empedans tabiri, değişken
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
akım devrelerinde akıma gösterilen zorluk olarak tanımlanmakta olup, ileriki derslerinizde ele
alınacaktır.
Eğer sabit gerilim çıkışı verebildiği halde (0’luk yük direnci uçlarına bağlı olmasına rağmen) iç direnci
sıfır olan bir gerilim kaynağına sahipseniz bu kaynağın bağlanan yüke sonsuz miktarda güç
aktarabildiğini söyleyebilirsiniz. Ancak P=V x I ifadesinden göreceğiniz gibi V sabit bir değerde
olduğuna göre sonsuz değerde güç elde etmek için akımın sonsuz olması gerekecektir.bu şartları
sağlamak tabii ki mümkün değildir. O yüzden kaynaklar ancak belirli bir RL değeri için maksimum güç
verebilirler. Bu RL değerinin daha az veya daha çok olduğu durumlarda kaynaktan çekilen güç
azalacaktır.
Sonuç olarak maksimum güç aktarım kuramı bir güç kaynağından ona bağlı olan yüke maksimum
miktarda güç aktarılabilmesi için kaynağın direnci ile RL yük direncinin eşit olması gerektiğini ifade
eder. Sonuçta güç kaynağı kaynağın iç direnci ve RL yük direnci seri bir devre oluşturacaktır ve
kaynağın ürettiği gücün bir kısmı iç direnç kalanı da yük direnci üzerine bölünecektir.
Şekil 7.1. Maksimum güç aktarım kuramı (devrenin toplam direnci kaynağın iç direnci ile yük direncinin
toplamıdır).
Kaynakların iç direnci kaynaktan yüke dağıtılan çıkış gerilimini değiştirdiği gibi kaynaktan çekilen akımı
da sınırlamaktadır.
Aşağıdaki devreler üzerinde düşünürken her üç devrenin de aynı kaynağı kullandığını farz edelim. İlk
devreye baktığınızda yük direnci ile kaynağın iç direncinin eşit olduğunu görüyoruz. Bu durumda yüke
aktarılan güç 10W’tır.
İkinci devrede yük direnci kaynağın iç direncinden daha küçüktür. Yüke aktarılan güç 8,84W olmuştur.
Üçüncü devrede yük direnci kaynağın iç direncinden daha büyük seçilmiştir. Bu durumda yüke
aktarılan güç 7,5W’tır.
Gördüğünüz gibi kaynağın iç direncinden daha büyük veya daha küçük değere sahip yük dirençleri
için elde edilen güç değeri yük direncinin değeri ile kaynağın iç direncinin eşit olması durumunda elde
edilen güç değerinden küçüktür. Bunun doğruluğunu ispatlamak için istediğiniz RL değerleri için yeni
hesaplar yapabilirsiniz. Sonuç kesinlikle değişmeyecektir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 7.2. Maksimum güç aktarım kuramının doğrulanması
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Verim
(%) Verim = (Pçıkış / Pgiriş) . 100
yukarıdaki hesaplamalarda verimlere dikkatle bakarsanız kaynaktan yüke en büyük miktarda gücün
aktarıldığı RL = rİÇ durumda verimin %50 olduğunu görürsünüz. Yani ilk şekilde gösterilen devre için
gerilim 20V, akım 1A ve toplam güç 20W iken yüke aktarılan güç 10W ve verim;
()= (10/20)x100 =%50’dir.
İkinci şekilde gerilim yine 20V, ama akım 1,33A’dir. Toplam güç 26,6W iken yüke aktarılan güç 8,84w
olmuştur. Bu durumda verim = (8,84 / 26,6).100 = %33,2’dir.
Son şekilde toplam güç 10W ve yükün çektiği güç 7,5W’tır. Bu durumda verim %75 olmuştur.
Şekil 7.3. Yük direnci ile yük gücünün değişim eğrisi
İlk şekilde kaynağın ürettiği güç 20W ve yüke aktarılan güç 10W, ikinci şekilde kaynağın ürettiği güç
26,6W ve yüke aktarılan güç 8,84W ve son olarak üçüncü şekilde kaynağın ürettiği 10W yüke aktarılan
7,5W olduğuna göre kaynağın ürettiği güç ile yüke aktarılan güç arasındaki farkı tüketen nedir? Bu
sorunun cevabı tabii ki iç direnç olacaktır. Diğer bir ifade ile yüke aktarılan güç en büyük değerine
ulaştığında kaynağın toplam direncinin yarısını iç direnç yarısını da yük harcamaktadır. İkinci devrede
iç direnç toplam gücün %67’sini ve üçüncü devrede ise %25’ini harcamaktadır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 7.4. Yük direnci ile verimin değişim eğrisi
Kaynağın çıkış uçlarındaki gerilimin yük akımı ile değiştiğinden habersiz olabilirsiniz. Bu duruma yol
açan kaynağın iç direnci üzerindeki gerilim düşümüdür. Yani yüksek yük akımları kaynak içinde daha
büyük gerilim düşümüne yol açarken kaynağın çıkış uçlarına daha düşük gerilim ulaşmasına sebep
olur. Kaynağın iç direncini ölçmek için çıkış uçları açık devre edildikten sonra gerilim ölçülür. Daha
sonra bu uçlar arasına akım çeken bir yük bağlanarak gerilim ölçümü yeniden tekrarlanır. Son
durumda çekilen akım da ölçülürse iç direnç için şu eşitliği kullanmak mümkün hale gelir.
riç = (Vyüksüz-Vyüklü) / Iyük
Örnek
Örnek olarak yüksüz durumdaki gerilimin 13V, yüklü durumda 12V ve yük bağlı iken çekilen akımın da
100A olduğunu farz edelim. Bu durumda riç değeri ne olur?
Çözüm
riç=13-12 / 100=0,01 olacaktır.
Özellikle akümülatörler üzerinde çalışan teknisyenler bu yöntemi sıklıkla kullanmaktadır. Ölçüm
sonucunda yük altındaki gerilim yüksüz duruma göre çok fazla düşerse, akünün bozulmuş veya
doldurmaya ihtiyaç duyduğuna karar verirler.
TOPLAMSALLIK KURAMI
Birden çok kaynağa sahip devre yapıları ile karşılaşmak mümkündür. Bu durumlarda toplamsallık
kuramının kullanılması faydalı bir çözümleme yolu olabilmektedir.toplamsallık kuramı birden fazla
kaynağa sahip lineer devrelerde herhangi bir eleman üzerinde düşen gerilim veya o elemandan geçen
akımın, kaynakların her birinin kendisi hariç diğer kaynaklar devre dışı bırakıldıktan sonra ürettiği
gerilim veya akımların cebirsel toplamına eşit olduğunu ifade eder. Her aşamada devrede sadece bir
kaynak bırakıldıktan sonra diğer kaynakların devre dışı edilmesi ile kastedilen devre dışı bırakılan
kaynak gerilim kaynağı ise devredeki uçlarının kısa devre edilmesi, akım kaynağı ise devredeki
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
uçlarının açık devre edilmesidir. Aşağıda verilen iki gerilim kaynağına sahip devrenin çözümlenmesi
için toplamsallık kuramını kullanalım.
Şekil 7.5. Toplamsallık kuramının doğrulanması.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Bu arada çok önemli bir noktanın altını çizelim : Her işlem adımında akım yönleri
düşümlerinin kutuplanmaları hesabın doğruluğu önemle dikkate alınmalıdır.
ve gerilim
Devrede öncelikle 60V’luk kaynak kısa devre edilerek devre dışı bırakılmıştır. Böylece R2 ve R3
dirençleri paralel olmuştur. Dolayısıyla R2 ve R3’ün paralel eşdeğeri ile R1 direnci seri bağlanmıştır.
Toplam direnç 3K’dur ve toplam akım 10mA olarak bulunur. Devrede kalan 30V’luk gerilim
kaynağının sağladığı 10mA’lik toplam akımın tamamı R1 üzerinden geçerken bu akım birbirine eşit
değere sahip R2 ve R3’ün bağlandığı noktadan itibaren 5’er mili amperlik iki parçaya bölünür. Ohm
kanununu kullanarak V1=20V ve V2=-10V bulunur. V1 ve V2 A noktasına göre bulunan değerlerdir. B
noktasına göre V3 gerilimi +10V’tur. (c) şeklinde 30V’luk kaynak devre dışı bırakılmış (kısa devre
edilmiş) ve 60V’luk kaynağa göre çözüm yapılmıştır. Bu durumda R1 ve R2 paralel bağlanmış bunların
paraleline de R3 direnci seri olarak eklenmiştir. R1 üzerindeki gerilim düşümü A noktasına göre 20V ,
R2 üzerindeki gerilim düşümü yine A noktasına göre 20V ve B noktasına göre R3 üzerindeki gerilim
düşümü 40V’tur.
(d) şeklinde hesaplanan sonuçların cebirsel toplamını görüyorsunuz. V1 gerilimi 30V’luk kaynak
devrede iken +20V ve 60V’luk kaynak devrede iken yine +20V idi. Sonuçta her iki adımdaki değerlerin
toplamı olan 40V‘tur ve V1=40V yazabiliriz. Hesaplanan bu V1 değeri A noktasına göre R1 üzerine
düşen gerilimdir. Aynı tür bir hesaplamayı V2 için de yaparsak A noktasına göre V2=10V ve R3
üzerindeki gerilim düşümü V3 de B noktasına göre 50V olarak bulunur.
Benzer şekilde her bir elemandan geçen akımların yönleri ve değerleri de belirlenebilir. (b) şeklinde
akım R2 direnci üzerinden B noktasından A noktasına doğru akmaktadır. Bu akımın değeri 5mA’dir.
(c) şeklinde R2 üzerinden akan akımın yönü A noktasından B noktasına doğrudur ve değeri 10mA’dir.
Bu iki değerin cebirsel toplamı 5mA olup her iki kaynak devrede iken R2 üzerinden akan akım A
noktasından B noktasına doğru bir yöne sahiptir.
Şekil 7.6. Toplamsallık kuramı için bir diğer örnek
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Çözüm için kullandığımız bu devrede devre tasarımı aynı kalmak şartıyla kaynakların kutuplanmaları
değiştirildiğinde akım ve gerilimlerin nasıl etkileneceğine bakalım. Bu durumda devremiz aşağıdaki gibi
olacaktır.
Çözüm için aynı şekilde hareket edeceğiz. Yani kaynak sayısı kadar işlem adımımız olacak, her bir
adımda sırası ile tek bir kaynak devrede bırakılırken diğer kaynaklar devre dışı edilecek , devre dışı
edilen kaynak gerilim kaynağı ise devredeki uçları kısa devre edilirken , akım kaynakları için bu işlem
devredeki uçların açık devre edilmesi şeklinde gerçekleştirilecektir.
İlk olarak 60V’luk kaynağı kısa devre edip 30V’luk kaynağa göre çözüm yapalım. A noktasına göre
V1= -20V ve V2=+10V bulunacaktır. B noktasına göre V3=-10V’tur.
İkinci adımda 30V’luk kaynağı kısa devre edip 60V2luk kaynağı devrede bırakarak çözümü
gerçekleştirelim. A noktasına göre V1=-20V, V2=-20V ve B noktasına göre V3=-40V olarak
bulunacaktır.
Son olarak her iki adımda hesaplanan değerleri birleştirirsek A noktasına göre V1=-40V ,V2=-10V ve B
noktasına göre V3=-50V değerleri elde edilir.
Dikkatlice bakarsanız hemen fark edeceğiniz gibi kaynakların kutuplanmalarının değiştirilmesi gerilim
düşümlerinin kutuplanmalarını ve akım yönlerini değiştirmiş, ama değerler kesinlikle değişmemiştir.
Toplamsallık kuramının uygulamalarına ait çözümlerden görülüyor ki, bu yöntemin kullanımında aynı
anda sadece bir kaynak devrede bırakılmakta ve ohm kanunundan faydalanılmaktadır. Kaynak sayısı
kadar çözüm aşaması tamamlandıktan sonra her bir adımda elde edilen değerler cebirsel olarak
toplanarak istenen elektriki büyüklükler hesaplanmaktadır.
THEVENİN KURAMI
Thevenin kuramı, iki nokta arasında akan akımın veya düşen gerilimin hesaplanması istenen karmaşık
devreleri basitleştirmeye dönük bir yöntemdir. Bunun için Thevenin eşdeğer devresi denilen basit
devreye dönüşüm gerçekleştirilir ve sadece iki seri dirençten ve bir kaynağından oluşan bu çok basit
devre kullanılarak istenen değerler hesaplanır. Burada bahsedilen gerilim kaynağı, çözüm sırasında
belirlenen değere sahip ve bu değeri değişmeyen bir gerilim kaynağıdır.
Thevenin kuramı ile herhangi iki uçlu doğrusal ağ ile (dirençlerden ve kaynaklardan oluşabilir) sadece
bir adet gerilim kaynağı (VTH) ve bir adet seri dirençten (RTH)oluşan eşdeğer devreye indirgenebilir.
Aşağıda Thevenin kuramı eşdeğer devresi gösterilmektedir.
Şekil 7.7. Thevenin kuramı eşdeğer devresi.
Aşağıdaki şekilde ise Thevenin kuramının uygulanması adımları gösterilmektedir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 7.8. Thevenin kuramı uygulama adımları.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Yukarıda verilen (b) şeklinde VTH’ın belirlenmesi gösterilmektedir. Bu sırada A ve B noktalarının açık
devre edildiğine dikkat ediniz. Başlangıçta çözüm A ve B noktalarının arasına ilişkin olarak
istendiğinden hesaplanacak açık devre gerilimi için A ve B noktaların arasının açılması gerekmektedir.
Yani VTH , A-B arası açık devre iken hesaplanan açık devre gerilimidir. Bu durumda ohm kanununu
kullanarak A-B arasından bakıldığında görülen toplam direnç RT=(100 // 100)+25+25=100, VT=100V
ve IT=1A bulunur. Kaynağa ve birbirlerine göre seri bağlı olan 25’luk dirençlerde 25’er Volt gerilim
düşümü olacaktır. 1A’lik toplam akım 100’er ohm değerine sahip iki paralel dirence iki eşit parça
halinde bölünecektir. Böylece A-B arasındaki gerilim VTH=0,5A x 100=50V olarak bulunacaktır.
Thevenin kuramının ikinci adımı RTH’ın bulunmasıdır. Ve bunun için (c) şeklinde gösterilen yol takip
edilir. gerilim kaynağı devreden çıkarılarak devredeki uçları kısa devre edildikten sonra A ve B
noktaları arasından bakıldığında görülen direnç (RTH) hesaplanır. Bu durumda 100’luk iki direnç
paralel bağlıdır. 25’er ohmluk iki seri direncin eşdeğeri olan 50’luk direnç te 100’luk dirençlere
paralel bağlıdır. Paralel bağlı 100’luk dirençlerin eşdeğeri 50 ve bu 50’la 25’er ohmluk iki seri
direncin eşdeğeri olan 50’luk direncin de paralel eşdeğeri 25’dur. Bu RTH’tır. Böylece ilk adımda
elde edilen VTH=50V’luk gerilim kaynağı ile ikinci adımda elde edilen R TH=25’luk direnç seri
bağlanarak açıkta kalan iki ucu A ve B olarak isimlendirmek suretiyle elde ettiğimiz basit devre asıl
devrenin birebir eşdeğeridir ve Thevenin eşdeğer devresi adını alır. Asıl devrede A ve B noktaları
arasındaki akım yönü ne ise eşdeğer devrede de o olmalıdır. Yani eşdeğer devrede A ve B
noktalarının kutuplanmaları değişmemelidir. Dikkat ederseniz asıl devrede akım yönü A’dan B’ye
doğrudur ve eşdeğer devrede bu korunmuştur.
Bütün bunlardan sonra RL=25 için IL=VTH / (RTH+RL)=50V / (25+25)=1A bulunacaktır.
VL=RL / (RL+RTH) x VTH = 25 / (25+25) x 50V=25V
Yük gerilimini hesaplarken gerilim bölücü kuralını kullandığımıza dikkat ediniz.
Görüldüğü gibi Thevenin kuramı ile karmaşık bir elektrik devresinin herhangi bir bölgesine ilişkin çok
basit bir eşdeğer devre elde edilmekte ve çözüm oldukça kolaylaşmaktadır. Burada herhangi bir bölge
tabiri ile kastedilen çözümde gördüğünüz ve A ve B noktaları olarak adlandırılan kısım olup A ve B
arasında sadece bir RL elemanı bulunabileceği gibi değişik elemanlarla oluşturulan devre yapıları da
bulunabilir.
Örnek
Weston köprü devresinin A ve B olarak adlandırılan uçları arasına bir RL yük direnci koyduğumuzu
farz edelim. Thevenin kuramını kullanarak akım ve gerilim değerlerini belirleyelim.
Çözüm (Aşağıda verilmiştir)
Öncelikle köprünün A ve B noktalarına göre Thevenin eşdeğer devresinin oluşturmalıyız.
1) A ve B noktaları arasındaki açık devre geriliminin, yani VTH’ın bulunması:
VTH = (VA-VB) = (R2 / R1+R2) . VS - (R4 / R3+R4).VS = 220/320.12-470/800.12 = 8,25-7,05 = 1,2V
2) RTH’ın bulunması (kaynak uçları kısa devre edilerek):
RTH=R1//R2 + R3//R4 =262,625
Bu aşamada çözüm yaparken A ve B noktalarını özellikle koruduğumuza dikkat ediniz. Önceki
konulardan hatırlamanız gerektiği gibi bir elektrik devresinde direnç nereden bakıldığına göre değişir.
Biz burada A ve B arasından bakıldığında görülen eşdeğer direnci bulmak gerektiği için A ve B
noktalarını korumak zorundayız.
3) RTH ve VTH’ı hesapladığımıza göre Thevenin eşdeğer devresini çizebiliriz.
Eşdeğer devrede en başta belirttiğimiz RL’yi A ve B noktaları arasına bağlarsak RL üzerinde düşen
gerilim ve içinden geçen akımı kolayca hesaplayabiliriz.
VRL = RL / (RTH+RL).VTH=270 / (263+270).1,2 = 0,61V
IL = VTH / RT = 1,2 / 533 = 2,25mA
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 7.9. Thevenin kuramının kullanılması ile Weston köprü devresinin çözümlenmesi
Şekil 7.10. Thevenin eşdeğer devresi .
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
NORTON KURAMI
Norton kuramı karmaşık ağların eşdeğer devrelere indirgenmesi ile basitleştirildiği diğer bir çözümleme
yöntemidir. Bu yöntem de Thevenin yöntemine benzer olarak ilgilenilen devre bölgesinin iki ucuna
göre yeni bir eşdeğer devrenin oluşturulması esasına dayanır. Farklı olarak çözüme akım üzerinden
gidilir.
Norton kuramına göre iki uçlu bir ağ, değeri değişmeyen tek bir akım kaynağı ile buna paralel bağlı bir
dirençten oluşan eşdeğer bir devre olarak ifade edilebilir. Bu eşdeğer devre aşağıda gösterilmektedir.
Şekil 7.11. Norton eşdeğer devresi
Öncelikle ilgilenilen iki uca A ve B isimleri verilir. Bu iki uç arasındaki eleman ya da elemanlar tümüyle
çıkarılarak bunların yerine bir kısa devre iletkeni bağlanır. Yani A ve B noktaları arası kısa devre edilir.
Bu durumda A ve B noktalarını birleştiren kısa devre iletkeninden akan ve IN diye adlandırılan kısa
devre akımı bulunur. Daha sonra Thevenin kuramında olduğu gibi A ve B arası açık devre iken ve
devredeki gerilim kaynakları kısa devre akım kaynakları da açık devre edilerek A-B arasından görülen
eşdeğer direnç (RN) hesaplanır. Thevenin kuramından farklı olarak bu RN direnci ile IN eşdeğer akım
kaynağı paralel bağlanacaktır.
Şekil 7.12 Norton eşdeğer devresi için IN kısa devre akımının bulunması. A-B arası kısa devre
edildiğinden IN=100V/50 = 2A olur.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 7.13 A-B arası açık devre edilerek RL’nin bulunması. Kaynak kısa devre edildiğinden
RN=RAB=25 bulunur.
Şekil 7.14. Thevenin ve Norton eşdeğer devrelerinin karşılaştırılması.
RL direncinin 25 olduğunu farz edelim. Öncelikle Norton eşdeğer parametrelerinin bulunması
gerekecektir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 7.15. Norton kuramının uygulama örneği
IN akımı RL kısa devre edildiğinde A ve B noktaları arsında akacak akımdır. Dikkat ederseniz RL’nin
kısa devre edilmesi 100’luk paralel dirençlerin de kısa devre edilmesi anlamına gelmiştir. Bu
durumda kısa devre yolundan akacak akım sadece 25’er ohmluk iki seri dirençten geçecek ve değeri
IN=100V/50=2A olacaktır.
RN direncini bulmak için asıl devreye geri dönmeli ve sadece A-B uçları arasını açıp gerilim
kaynaklarını kısa devre ve akım kaynaklarını açık devre yapmalıyız. Devremizde sadece bir gerilim
kaynağı olduğundan onun uçlarını kısa devre edip A-B uçlarını açık devre haline dönüştürdüğümüzde
A-B arasından görülen eşdeğer direnç RN=100 // 100 // (25+25) =25 olarak bulunacaktır. Son olarak
değeri 2A olan akım kaynağı ile değeri 25 olan Norton eşdeğer direncini paralel bağlayıp bu ikisinin
bağlandığı uçlar arasına RL’yi de paralel olarak yerleştirebiliriz. Eşdeğer devrede A ve B noktalarını
belirlerken asıl devredeki akım yönüne dikkat etmek gerektiğini tekrar belirtelim. Eşdeğer devrede RN
ve RL’nin birbirine eşit ve 25 değerinde olduğunu görüyoruz. Bunun anlamı akım kaynağından çıkan
2A’lik akımın her iki dirence 1’er amper olarak bölüneceğidir. Yani IL=1A ve ILxRL=1Ax25=25V olur.
Aynı devrenin Thevenin kuramını anlatırken de kullanıldığını hatırlayıp çözümlerini karşılaştırırsanız
sonuçların aynı olduğunu göreceksiniz.
RL=75 olsaydı IL akımının bulunması için akım bölücü kuralını kullanmak gerekecekti. Bu durumda;
IL=RN / (RN+RL) . IN olacaktır.
Öyleyse IL=25/(25+75).2 = 0,5A olarak bulunacaktı. Bu şartlarda VL=0,5 . 75 = 37,5V olur.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
NORTON VE THEVENİN EŞDEĞER PARAMETRELERİNİN BİRBİRİNE DÖNÜŞTÜRÜLMESİ
Norton parametrelerinden Thevenin parametrelerini elde etmek için şunlar yapılır:
RTH=RN
VTH=IN x RN
Thevenin parametrelerinden Norton parametrelerinin bulunması:
RN=RTH
IN=VTH/RTH
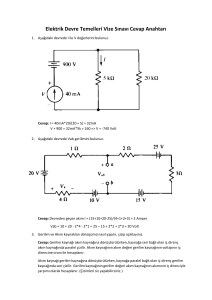
Örnek
Aşağıdaki devre için Thevenin ve Norton eşdeğer parametrelerini bulup birbirine dönüştürün.
Çözüm
Thevenin kuramı:
Dönüşümler:
VTH=Re1/(Re1+Re2).20V = 253/(253+280).20=9,5V
RTH=Re1 // Re2 =133
Nortondan Thevenine;
RTH=RN=133
VTH=IN x RN = 71mA x 133 =9,5V
Norton kuramı:
IN=V/Re2 = 20/280 = 71mA
RN=Re1 // Re2 =133
Theveninden Nortona:
RN=RTH=133
IN=VTH / RTH =9,5V / 133=71mA
Şekil 7.16. Thevenin ve Norton eşdeğer devreleri için bir uygulama örneği