ışığın kırılması

IŞIĞIN KIRILMASI
KIRILMALAR
Günlük hayatta çok sık rastladığımız ve
gözlemlediğimiz bir olaydır kırılma.
Bir su kuyusuna baktığımız zaman kuyunun dibini
daha yakında görürüz.
Çay bardağındaki kaşığı bardak içindeyken kırık
gibi görürüz.
Yazın asfalt üzerinde yağmur yağmış gibi serap
etkisi görülmesi.
Yıldızlardan gelen ışınların atmosferin
tabakalarından geçerken kırılması ve bize farklı
doğrultularda gözükmesi.
Güneş doğarken ve batarken ışığın kırılmasından
dolayı ufuğun kırmızı renkte görülmesi.
Yağmur sonrası ışığın yağmur damlalarında
kırılarak gökkuşağını oluşturması.
Boşluğun ve havanın kırıcılık indisi 1 olarak kabul
edilir.
Hiçbir ortamın mutlak kırılma indisi 1 den büyük
olamazken bağıl kırılma indisi olabilir.
Bir ışık ışınının ortamdaki hızı ile ortamın kırılma
indisi ters orantılıdır.
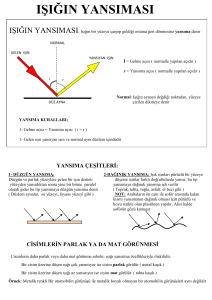
Kırılma Kanunları :
Gelen ışının ayırıcı yüzeye geldiği noktadan yüzeye çıkan
dik doğrultuya yüzey normali, gelen ışınla yüzey normali
arasındaki açıya ( i ) gelme açısı, kırılan ışınla yüzey
normali arasındaki açıya ( r ) kırılma açısı denir.
Hepsi ışığın kırılmasına birer örnektir.
Bir saydam ortamda ilerleyen bir ışın, farklı bir saydam
ortamla karşılaşınca ikinci ortamda doğrultusu değişmiş
olarak ilerler. Buna ışığın kırılması denir. Işık ışınlarının
kırılmasının temel nedeni, ışık hızının saydam ortamlarda
farklı değerler almasıdır. Işık ışınlarının her saydam
ortamdaki yayılma hızı birbirinden farklıdır.
1.) Gelen ışın, kırılan ışın ve yüzeyin normali aynı
düzlem içindedirler.
2.) Ortamları değiştirmemek şartıyla gelme açısının
sinüsünün, kırılma açısının sinüsüne oranı daima
sabittir.
n
Sini
= 2 = n12 = sabit
Sinr
n1
n1.Sin i = n2.Sin r
;
n1
Sinr V2
=
=
n2
Sini
V1
………… Snell Bağıntısı
Boşlukta her renk ışığın yayılma hızı 300 000 km/sn dir.
Ancak bir saydam ortamda her renk ışının yayılma hızı
birbirinden farklıdır.
Özel Durumlar:
Mutlak Kırıcılık indisi;
Bir saydam ortamın mutlak kırıcılık indisi, boşluktaki ışık
hızının ortamdaki ışık hızına oranı olarak tanımlanır.
n or =
c
v
or
Örneğin:
n su =
c
v
su
=
1.) Bir ışın bir yüzeye normal doğrultusunda gelirse
diğer ortama kırılmadan geçer. Ortamların kırıcılık
indislerinin bir önemi yoktur.
2.) Işığın frekansı sadece ışık kaynağına bağlıdır.
Kırıcılık indislerine, gelme ve yansıma açılarına
bağlı değildir.
300000 4
=
= 1,33
225000 3
Bir saydam ortamın başka bir saydam ortama göre olan
indisine bağıl kırıcılık indisi denir.
1. ortamın 2. ortama göre bağıl kırıcılık indisi ;
Sinr
=
Sini
n1 = n
2,1
n2
Kırıcılık indisi büyük olan ortamlara çok yoğun
ortam, kırıcılık indisi küçük olan ortamlara az yoğun
ortam denir. Burada ki yoğunluk optik yoğunluk
anlamındadır. Özkütle ile ilgisi yoktur.
3.) Kırıcılık indisleri eşit olan iki ortamdan ışık geçerken
kırılmaya uğramaz.
Işığın çok yoğun ortama geçişi:
Bir ışın az yoğun ortamdan çok yoğun ortama geçerken
normale yaklaşarak kırılmaya uğrar.
n1 ⟩ n 2
n1.Sin i = n2.Sin 90
Sin 90 = 1
n2
i = sınır açısı
Sin i =
n1
n1 ⟨n 2
i⟩ r
Bir ışın az yoğundan çok yoğun ortama geçerken ışın
her zaman diğer ortama geçer, yansıma olayı
görülmez.
Ortamların kırıcılık indisleri arasındaki fark arttıkça ışık
ikinci ortama geçerken daha fazla kırılır.
Gelme açısı ( i ) arttıkça, yansıma açısı (r) da artar.
Ortamlar için sınır açısı kritik açıdır.Gelme açısı artırılırsa
ışın tam yansıma yapar, gelme açısı azaltılırsa ışın
normalden uzaklaşarak kırılır.
Ortamlar arasındaki kırıcılık indisleri farkı artırılırsa tam
yansıma, azaltılırsa normalden uzaklaşarak kırılır.
4.)
Tam yansıma da gelme açısı yansıma açısına
eşittir.
Işığın az yoğun ortama geçişi:
Bir ışın çok yoğun ortamdan az yoğun ortama geçerken üç
durum söz konusu olabilir.
1.) Gelen ışın normalden uzaklaşarak kırılabilir.
2.) Gelen ışın sınırdan geçebilir.
3.) Gelen ışın tam yansımaya uğrayabilir.
Işıkta tersinirlik:
Bir ışık ışını gittiği yoldan aynen geridöner. Buna ışığın
tersinirliği denir.
n1 ⟩ n 2
1.) Bir ışın az yoğun ortama geçerken normalden
uzaklaşır.
n1 ⟩ n 2
Küresel Ortamlarda Kırılma :
Küresel ortamlarda yüzey normali merkezden gelen çizgi
doğrultusudur.
r⟩ i
Gelme açısı (i) artarsa, yansıma açısı (r)‘da artar.
3.) Bir ışın çok yoğun ortama geçerken sınırdan da
geçebilir. Işığın normalle yaptığı açıya sınır açısı
denir.
Küresel bir yüzeyin merkezinden gelen veya merkez
doğrultusunda gelen ışın diğer ortama kırılmadan geçer.
Su ortamından hava ortamındaki bir cisme bakan bir
gözlemci, cismi kendisinden uzaklaşmış olarak görür.
Paralel Yüzlü Ortamlar:
Paralel yüzlü ortamlarda ilerleyen ışının normalle yaptığı açı
ne kadar büyükse o ortamın kırıcılık indisi de o kadar
küçüktür.
h' =
n göz
n cisim
.h =
n su
⋅h
n hava
s > i > r ise n 2 ⟩n1 ⟩n 3
Paralel ortamlar içindeki bir cismin zahiri derinliği:
Paralel bir ortama gelen ışınla aynı ortamdan çıkan ışın
birbirine paraleldir.
Işının sapma miktarı olan x, ortamların kırılma indislerine,
gelme açısına ve paralel ortamın kalınlığına (d) bağlıdır.
x = d.
Sin(i − r )
cos r
Zahiri Derinlik :
Hava ortamından su içindeki bir cisme bakan gözlemci,
cismi kendine yaklaşmış olarak görür.
h' =
h1 h 2 h 3
+
+
n1 n 2 n 3
Paralel ortamlar dışındaki bir cismin zahiri yüksekliği:
h' = h1.n1 + h 2 .n 2 + h 3 .n 3
h' =
n göz
n cisim
.h =
n hava
⋅h
n su
= θ1 + θ2 - A
Bir prizmada, prizmanın bir yüzeyine gelen ışık ışını için
minumum sapma açısı vardır. Işık ışını daha küçük bir
sapmaya uğrayamaz.prizmada kırılarak perdeye düşer.
Sapma açısının minumum olduğu durum;
Küresel saydam cisimler içinde zahiri derinlik;
1. Küresel cisimlerin merkezinden gelen ışınlar dik
olduklarından kırılmaya uğramaz ve merkezde
bulunan cisim yine olduğu yerde görülür.
θ1 = θ2 ve β1 = β2
dur.
Özel durum:
Camdan yapılmış bir prizmanın hava ortamına göre sınır
o
açısı 42 dir.
Çok yoğundan az yoğuna sınır açısından daha küçük
açıyla gelen bir ışın diğer ortama normale yaklaşarak
kırılarak geçer.
2. Cisim merkezden daha yakında ise görüntüsü de
daha yakında görünür.
Çok yoğundan az yoğuna sınır açısıyla gelen ışın
ortamları ayıran çizgiden yani sınırdan geçer.
3. Cisim merkezden daha uzakta ise görüntüsü de
daha uzakta görünür.
Çok yoğundan az yoğuna sınır açısından daha büyük
açıyla gelen bir ışın tam yansıma yapar, diğer ortama
geçemez.
Bir ışık kaynağının prizmalardaki görüntüsü kırılan ışığın
uzantılarının kesiştiği noktada oluşur.
Prizmalar:
Dik kesiti üçgen şeklinde olan saydam prizmalara ışık
prizmaları denir.hava ortamında iken, ışık prizmaları ışık
ışınlarını daima tabana yaklaştıracak şekilde kırarlar.
Đkizkenar dik üçgen şeklindeki prizmalara tam yansımalı
prizmalar denir.
A = β1+β2
Prizma için sapma açısı ( D ) :
D = ( θ1 - β1 ) + ( θ2 - β2 )
= θ1 + θ2 - ( β1 + β2 )