FİBONACCİ DİZİSİ VE ALTIN ORAN
Leonardo Fibonacci, (Pisalı Leonardo,
Leonardo Pisano d. 1170, ö. 1250), yaygın
olarak ismiyle Fibonacci diye anılan, orta
çağın en yetenekli matematikçisi olarak
kabul edilen İtalyan matematikçi.
Orta çağın en büyük matematikçilerinden biri olarak kabul
edilen Fibonacci İtalya'nın ünlü Pisa şehrinde doğmuştur.
Çocukluğu babasının çalıştığı Cezayir'de geçmiştir. İlk
matematik eğitimini Müslüman bilim adamlarından almış,
İslam aleminin kitaplarını incelemiş ve bunlar üzerinde
çalışmıştır. Avrupa'da Roma rakamları kullanılırken ve
sıfır kavramı ortalarda yokken Leonardo Fibonacci Arap
rakamlarını ve sıfırı öğrenmiştir.
1201 yılında "Liber Abacci" adında bir matematik
kitabı yazmıştır. Bu kitapla Avrupa'ya Arap
rakamlarını ve bugün kullandığımız sayı sistemini
tanıtmıştır. Bu kitapta temel matematik
kurallarını birçok örnek vererek anlatmıştır.
I = 1 , V = 5, X = 10, L = 50, C = 100, D = 500, M =
1000
Bu rakamlarla 13 XIII ve ya IIIX şeklinde, 2003
MMIII şeklinde, 99 LXXXXVIIII şeklinde ve 1998
MDCCCCLXXXXVIII şeklinde yazılır.
CCXXIII + XXVIII = CCI
CLXXIIII - XXVIII = CXXXXVI
Bu bakımdan Fibonacci, matematiği Araplardan alıp
Avrupa’ya tanıtan kişi olarak anılır. Avrupalıları roma
rakamlarının hantallığından kurtararak hint-arap sayı
sisteminin yaygınlaşmasını sağlamıştır.
FİBONACCİ DİZİSİ
Her sayının kendinden öncekiyle toplanması sonucu
oluşan bir sayı dizisidir.
Buna göre Fibonacci dizisi şöyle tanımlanır:
F1 = 1, F2 = 1
Fn = Fn-1 + Fn-2 , n>2
Buna göre Fibonacci sayılarının ilk birkaç tanesi
şöyle sıralanır:
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,159
7,2584,4181,6765,10946...
Peki Fibonacci sayılarını ortaya çıkaran soru neydi?
"Bir çift yavru tavşan ( bir erkek ve bir dişi) var. Bir
ay sonra bu yavrular erginleşiyor. Erginleşen her çift
tavşan bir ay sonra bir çift yavru doğuruyorlar. Her
yavru tavşan bir ay sonra erginleşiyorlar. Hiç bir
tavşanın ölmediğini ve her dişi tavşanın bir erkek bir
dişi yavru doğurduğunu varsayarsak bir yıl sonra kaç
tane tavşan olur?"
Fibonacci dizisini bu kadar ilginç kılan nedir?
Fibonacci sayılarına özellikle doğada çok sık
rastlamaktayız. Bu sayılar bitki yaprakları, bitki
tohumları, çiçek yaprakları ve kozalaklarda sıkça
karşımıza çıkmaktadır. Daha da ilginci bu sayılara
Pascal veya Binom üçgeninde, Mimar Sinan’ın
eserlerinde, Da Vinci’nin resimlerinde de
rastlanmaktadır.
Bu yönüyle Fibonacci dizisine doğanın
matematiksel şifresi adı verilmektedir.
Eğer bir bitkiyi dikkatle incelerseniz fark edersiniz
ki, yapraklar, hiç bir yaprak alttaki yaprağı
kapatmayacak şekilde dizilmiştir. Bu da demektir ki,
her bir yaprak güneş ışığını eşit bir şekilde paylaşıyor
ve yağmur damlaları bitkinin her bir yaprağına
değebiliyor. Bir bitkinin sapındaki yapraklarda, bir
ağacın dallarının üzerinde hemen her zaman Fibonacci
sayıları bulursunuz.
• Mesela, yandaki
resimde en baştaki
dalı incelersek,
başlangıç noktası
olarak 1 numaralı
yaprağı alırsak,
kendisiyle aynı yönde
bir başka yaprakla
karşılaşabilmemiz için
3 defa saat yönünde
bir dönüş yapmamız
gerekir ve bu esnada
5 tane yaprak sayarız.
Eğer bu dönüşü saat
yönünün tersinde
yaparsak 2 tane dönüş
gerekecektir. Ve 2, 3,
5 ardışık fibonacci
sayıları elde
edilecektir.
Bitkilerde bir yapraktan başlayıp gövde etrafında
dönerek aynı doğrultudaki diğer yaprağa
rastlayıncaya kadar yapmamız gereken tur sayısı ile
bu turlar sırasında karşılaştığımız yaprak sayılarını
sırasıyla p ve n ile gösterirsek p/n oranına yaprak
divergesi denir.
Yandaki şekil için yaprak divergesi 5/8 dir.
Büyüme açısı (360x2)/5=144 derecedir.
Çiçek sapı üzerinde yaprakların ideal dizilişi için
büyüme açısı:
2Л/φ^2=137 bu açı değerine altın açı adı verilir.
Yeni doğan her dal,
ikinci yılını
tamamladıktan sonra
her yıl yeni bir dal
verir. Bu kural yeni
doğan dallar için de
geçerlidir. Buna göre
her yıl kaç dal
olduğunu sayarsak 1,
1, 2, 3, 5, 8, 13, ...
dizisini buluruz
Fibonacci sayıları ayrıca
çiçeklerin tohumlarında
da görülebilir. Eğer bir
papatyanın ve ya bir
ayçiçeğinin çiçek kısmını
büyütseniz muhtemelen
yandaki resme benzer bir
görüntü elde edersiniz.
Eğer şekildeki modelde,
saat yönünde olan ve saat
yönünde olmayan
sarmalları sayarsanız, 21
ve 34 sayılarını elde
edersiniz ki bu sayılar
ardışık iki fibonacci
sayısıdır.
Fibonacci sayılarına sadece
ayçiçeklerinde ve ya
papatyalarda değil, bir
kıvırcığın yapraklarında bir
ananas veya kozalakların kat
kat kabuklarında, soğanın
katmanları arasında da
rastlayabilirsiniz. Kozalaklar
fibonacci sayılarını çok açık bir
şekilde gösterirler.
Kırmızı ve yeşil spiralleri
saydığınızda ne görüyorsunuz?
Phi Sayısı Dediğimiz Bu Altın Oran Nedir
ve Fibonacci Dizisiyle Ne Alakası Vardır?
Φ , φ sayısı matematikte bulunan gizemli sayılar
arasında en özelidir ve bu özelliğinden dolayı buna Altın
oran denilmiştir.
Fibonacci dizisi ile alakasına gelince; Fibonacci dizisinin
her teriminin bir önceki terimine oranı bize altın oranı
verir. Φ sayısının yaklaşık değeri ise 1.618’ dır.
Altın orana ilişkin matematik bilgisi ilk kez İ.Ö. 3. Yüzyılda
Öklid’in Stoikheia ("Öğeler") adlı yapıtında "aşıt ve
ortalama oran" adıyla kayda geçirilmiştir. Eldeki veriler, bu
bilginin geçmişinin aslında Eski Mısır’da İ.Ö. 3000 yılına
kadar dayandığını göstermektedir
ALTIN ORAN
•
•
•
•
Altın oran, günlük yaşantımızda, matematiğin estetik
güzelliğe etki ettiği her alanda karşımıza çıkan bir
kavramdır. Altın oranın çok çeşitli tanımları verilebilir
ama altın oran, neticede matematiksel bir kavramdır ve
değeri de 1,618033.... olarak devam eden ondalık bir
sayıdır.
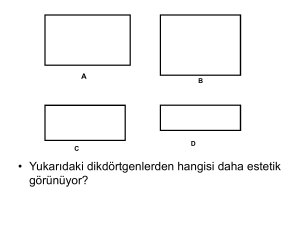
Altın oran, örneğin bir dikdörtgenin göze en estetik
gözükmesi için uzun kenarı ile kısa kenarı arasındaki
orandır.
Buna benzer olarak, bir doğru parçasının ikiye
ayrıldığında göze en hoş gelen ikiye ayrılma oranıdır.
Altın oran, sadece dikdörtgen ve doğru için değil,
neredeyse tüm geometrik cisimler ve yapılar için
kullanılabilir.
Altın oranın matematiksel açıdan basit bir tanımı şu
şekilde yapılabilir:
Altın oran, 1 sayısına eklendiğinde kendi karesine eşit
olan iki sayıdan biridir. Altın oran 1,618033.... olarak
devam eden ondalık sayıdır. 1 sayısına eklendiğinde
kendi karesine eşit olan diğer sayı da - 0,618033... olarak
devam eden ondalık sayıdır.
Altın Oranın Görüldüğü Ve Kullanıldığı Yerler:
1) Ayçiçeği: Ayçiçeği'nin merkezinden dışarıya doğru
sağdan sola ve soldan sağa doğru tane sayılarının birbirine
oranı altın oranı verir.
2) Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde
olduğu gibi bir altın oran mevcuttur
3) İnsan Kafası: Bildiğiniz gibi her insanın kafasında bir
ya da birden fazla saçların çıktığı düğüm noktası
denilen bir nokta vardır. İşte bu noktadan çıkan saçlar
doğrusal yani dik değil, bir spiral, bir eğri yaparak
çıkmaktadır. İşte bu spiralin ya da eğrinin tanjantı yani
eğrilik açısı bize altın oranı verecektir.
4) İnsan Vücudu: İnsan Vücudunda Altın Oran'ın
nerelerde görüldüğüne bakalım:
a) Kollar: İnsan vücudunun bir parçası olan kolları dirsek
iki bölüme ayırır.(Büyük(üst) bölüm ve küçük(alt) bölüm
olarak). Kolumuzun üst bölümünün alt bölüme oranı altın
oranı vereceği gibi, kolumuzun tamamının üst bölüme
oranı yine altın oranı verir.
b) Parmaklar: Ellerimizdeki parmaklarla altın oranın ne
alakası var diyebilirsiniz. İşte size alaka...
Parmaklarınızın üst boğumunun alt boğuma oranı altın
oranı vereceği gibi, parmağınızın tamamının üst boğuma
oranı yine altın oranı verir.
Parmaklarımız üç boğumludur. Parmağın tam
boyunun İlk iki boğuma oranı altın oranı verir (baş
parmak dışındaki parmaklar için). Ayrıca orta
parmağın serçe parmağına oranında da altın oran
olduğunu fark edebilirsiniz.
2 eliniz var, iki elinizdeki parmaklar 3 bölümden
oluşur. Her elinizde 5 parmak vardır ve bunlardan
sadece 8'i altın orana göre boğumlanmıştır. 2, 3, 5
ve 8 fibonocci sayılarına uyar.
İnsan Yüzünde Altın Oran
• İnsan yüzünde de birçok
altın oran vardır. Ancak
bunu elinize hemen bir
cetvel alıp insanların
yüzünde ölçüler almayı
denemeyin. Çünkü bu
oranlandırma, bilim
adamları ve sanatkarların
beraberce kabul ettikleri
"ideal bir insan yüzü" için
geçerlidir.
•
Her uzun çizginin kısa
çizgiye oranı altın orana
denktir.
• Örneğin üst çenedeki ön iki
dişin enlerinin toplamının
boylarına oranı altın oranı
verir. İlk dişin genişliğinin
merkezden ikinci dişe oranı
da altın orana dayanır.
Bunlar bir dişçinin dikkate
alabileceği en ideal
oranlardır.
Yüzün boyu / Yüzün genişliği,
Dudak- kaşların birleşim yeri arası / Burun boyu,
Yüzün boyu / Çene ucu-kaşların birleşim yeri arası,
Ağız boyu / Burun genişliği,
Burun genişliği / Burun delikleri arası,
Göz bebekleri arası / Kaşlar arası.
Akciğerlerdeki Altın Oran
Amerikalı fizikçi B. J. West ile doktor A. L. Goldberger,
1985-1987 yılları arasında yürüttükleri
araştırmalarında, akciğerlerin yapısındaki altın oranının
varlığını ortaya koydular. Akciğeri oluşturan bronş
ağacının bir özelliği, asimetrik olmasıdır. Örneğin, soluk
borusu, biri uzun (sol) ve diğeri de kısa (sağ) olmak
üzere iki ana bronşa ayrılır. Ve bu asimetrik bölünme,
bronşların ardışık dallanmalarında da sürüp gider. İşte
bu bölünmelerin hepsinde kısa bronşun uzun bronşa olan
oranının yaklaşık olarak 1/ 1,618 değerini verdiği
saptanmıştır.
5) Tavşan: İnsan kafasında olduğu gibi tavşanda da
aynı özellik vardır.
6) Mısır Piramitleri: İşte size Altın Oran'ın en eski
örneklerinden biri... Şimdi ne alaka Altın Oran ve
Milattan Önce yapılan Mısır Piramitleri? Alaka şu; Her
bir piramidin tabanının yüksekliğine oranı evet yine altın
oranı veriyor.
7) Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci
Rönesans devri ünlü ressamlarındandır. Şimdi bu
ünlü ressamın çizmiş olduğu tabloları inceleyelim.
a) Mona Lisa: Mona Lisa'nın başının etrafına bir
dikdörtgen çizdiğinizde ortaya çıkan dört kenar bir altın
dikdörtgendir. Bu dikdörtgeni, göz hizasında çizeceğiniz
bir çizgiyle ikiye ayırdığınızda yine bir altın oran elde
edersiniz. Resmin boyutları da altın oran
oluşturmaktadır.
Leonardo doğadaki bu mucizevi aritmetiği
resimlerinde kullandı. Böylece gerçeğe yani
mükemmele en yakın eserleri verebildi. Örneğin
insan vücudunda uzuvların mesafeleri arasında da
altın oran söz konusu. Üç resimde de resmin tam
ortasından geçen çizgi gözlerden birinin ortasından
geçiyor. Altın orana bağlı olan üçgenin içinde vücut
oturur.
Çene ve kulaklardan hiza alan kafanın ebatları tam bir
karedir. Onun altına altın oranı yani 1.618 oranında
ölçüyü eklerseniz koltukaltı hizasına ulaşılır. En
mükemmel portrelerde portrenin tam ortasından
indirilen çizginin gözlerden birinin ortasından geçmesi
de sanatta matematiğe işaret eder. Yani gözlemledi,
doğanın matematiğini keşfetti ve matematikle, sanatı
harmanladı. Da Vinci’nin bir şifresi yok. O doğanın
şifresini çözdü.
b) Aziz Jerome: Yine tablonun boyunun enine oranı
bize altın oranı verir.
8) Picasso: Picasso da Leonardo da Vinci gibi ünlü bir
ressamdır. Ve resimlerinde bu oranı kullanmıştır.
Özellikle "isa'nın Son Akşam Yemeği" adlı yapıtında
kullandığı teknikler Rönesans döneminde İzdüşümsel
Geometri (biçimlerin izdüşümlerinin özellikleri ve uzaysal
ilişkileri ile uğraşan, matematiğin bir alanı) nin ilk sanatsal
boyutu olarak karşımıza çıkmaktadır.
Burada ressam iki boyutlu tuvale üç boyutlu bir
manzarayı resmederken değişik uzaklık ve konumların
manzaradaki öğeleri nasıl etkileyeceğine karar verir. Bu
noktada çizim tekniklerinde perspektif (geometri) ve farklı
doğruların bir odak noktaya göre hareketlerini
(izdüşümsel geometri) dikkate alır.
9) Çam Kozalağı: Çam
kozalağındaki taneler kozalağın
altındaki sabit bir noktadan
kozalağın tepesindeki başka bir
sabit noktaya doğru spiraller
(eğriler) oluşturarak çıkarlar. İşte
bu eğrinin eğrilik açısı altın
orandır.
10) Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz
kabuklarına dikkat edenimiz, belki de koleksiyon
yapanımız vardır. İşte deniz kabuğunun yapısı
incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin
tanjantının altın oran olduğu görülmüştür.
Bilim adamları deniz dibinde yaşayan ve yumuşakça olarak
sınıflandırılan canlıların taşıdıkları kabukların yapısını incelerken
bunların formu, iç ve dış yüzeylerinin yapısı dikkatlerini çekmiştir:
"iç yüzey pürüzsüz, dış yüzeyde yivliydi. yumuşakça kabuğun içindeydi
ve kabukların iç yüzeyi pürüzsüz olmalıydı. kabuğun dış köşeleri
kabukların sertliğini artırıyor ve böylelikle, gücünü yükseltiyordu. kabuk
formları yaratılışlarında kullanılan mükemmellik ve faydalarıyla hayrete
düşürür. kabuklardaki spiral fikir mükemmel geometrik formda ve
şaşırtıcı güzellikteki 'bilenmiş' tasarımda ifade edilmiştir."
11) Tütün Bitkisi: Tütün Bitkisinin
yapraklarının dizilişinde bir eğrilik
söz konusudur. Bu eğriliğin
tanjantı altın orandır.
12) Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti
Otu'nda da vardır.
13) Salyangoz: Salyangozun Kabuğu bir düzleme
aktarılırsa, bu düzlem bir dikdörtgen oluşturur. İşte bu
dikdörtgenin boyunun enine oranı yine altın oranı verir.
Yumuşakçaların pek çoğunun sahip olduğu kabuk
logaritmik spiral şeklinde büyür. Bu canlıların hiçbiri
şüphesiz logaritmik spiral bir yana, en basit matematik
işleminden bile habersizdir.
Peki nasıl olup da söz konusu canlılar kendileri için en
ideal büyüme tarzının bu şekilde olduğunu
bilebiliyorlar?
Bazı bilim adamlarının "ilkel" olarak kabul ettiği bu
canlılar, bu şeklin kendileri için en ideal form olduğunu
nereden bilmektedirler?
Böyle bir büyüme şeklinin bir şuur ya da akıl olmadan
gerçekleşmesi imkansızdır. Bu şuur ne
yumuşakçalarda ne de -bazı bilim adamlarının iddia
ettiği gibi- doğanın kendisinde mevcuttur. Böyle bir şeyi
tesadüflerle açıklamaya kalkışmak çok büyük bir
akılsızlıktır. Bu ancak üstün bir aklın ve ilmin ürünü
olacak bir tasarımdır.
Birkaç santimetre çapındaki bir nautilusta, gnom tarzı
büyümenin en güzel örneklerinden birini görmek
mümkündür. C. Morrison insan zekası ile bile
planlaması hayli güç olan bu büyüme sürecini şöyle
anlatır:
"Nautilus'un kabuğunun içinde, sedef duvarlar ile
örülmüş bir sürü odacığın oluşturduğu içsel bir sarmal
uzanır. Hayvan büyüdükçe, sarmal kabuğunun ağız
kısmında, bir öncekinden daha büyük bir odacık inşa
eder ve arkasındaki kapıyı bir sedef tabakası ile örterek
daha geniş olan bu yeni bölüme ilerler."
Bugün fosil halinde bulunan ve Amonitlerde logaritmik
sarmal şeklinde gelişen kabuklar taşırlar.
Hayvanlar dünyasında sarmal formda büyüme sadece
yumuşakçaların kabukları ile sınırlı değildir. Özellikle
Antilop, yaban keçisi, koç gibi hayvanların boynuzları
gelişimlerini temelini altın orandan alan sarmallar şeklinde
tamamlarlar.
İşitme ve Denge Organında Altın Oran
İnsanın iç kulağında yer alan Cochlea (Salyangoz)
ses titreşimlerini aktarma işlevini görür. İçi sıvı dolu
olan bu kemiksi yapı, içinde altın oran barındıran 73
derece 43´ sabit açılı logaritmik sarmal
formundadır.
Sarmal Formda Gelişen Boynuzlar ve Dişler
Filler ile soyu tükenen mamutların dişleri, aslanların
tırnakları ve papağanların gagalarında logaritmik sarmal
kökenli yay parçalarına göre biçimlenmiş örneklere
rastlanır. Eperia örümceği de ağını daima logaritmik
sarmal şeklinde örer. Mikroorganizmalardan planktonlar
arasında, globigerinae, planorbis, vortex, terebra,
turitellae ve trochida gibi minicik canlıların hepsinin
sarmala göre inşa edilmiş bedenleri vardır.
Mikrodünyada Altın Oran
Geometrik şekiller sadece üçgen, kare veya beşgen,
altıgen ile kısıtlı değildir. Bu saydığımız şekiller
değişik şekillerde de biraraya gelerek yeni üç
boyutlu geometrik şekiller oluşturabilirler. Bu konuda
ilk olarak küp ve piramit örnek olarak verilebilir.
Ancak bunların dışında, günlük hayatta hiç
karşılaşmadığımız hatta ismini dahi ilk defa
duyduğumuz tetrahedron (düzgün dört yüzlü),
oktahedron, dodekahedron ve ikosahedron gibi üç
boyutlu şekillerde vardır. Dodekahadron 13 tane
beşgenden, ikosahedron ise 20 adet üçgenden
oluşur.
Bilim adamları bu şekilleri matematiksel olarak birbirine
dönüşebileceğini ve bu dönüşümün altın orana bağlı
oranlarla gerçekleştiğini bulmuşlardır.
16. Yüzyılda altın oran için
“hazine” ifadesini kullanan
Kepler, beş düzgün cisim
arasındaki geometrik
dönüşümlere çok önem vermiş
ve gezegenlerin yörüngeleri ile
bu cisimleri çevreleyen
küreler arasında bir bağlantı
kurmaya çalışmıştır.
Kepler, düzgün çok yüzlüleri iç
içe geçmiş şekilde gösteren ve
bu düzen ile Güneş Sistemi
arasındaki bağlantıyı araştıran
şemalar geliştirmiştir.
Mikroorganizmalarda altın oran barındıran üç boyutlu
formlar oldukça yaygındır. Birçok virüs ikosahedron
yapısında bir biçime sahiptir. Bunların en ünlüsü Adeno
virüsüdür. Adeno virüsünün protein kılıfı, 252 adet protein
alt biriminin düzenli bir biçimde dizilmesi ile oluşur.
İkosahedronun köşelerinde yer alan 12 alt birim ise
beşgen prizmalar biçimdedir. Bu köşelerden diken benzeri
yapılar uzanır.
Virüslerin altın oranları
bünyesinde barındıran
formlarda olduğunu tespit
eden ilk kişi 1950'li yıllarda
Londra'daki Birkbeck
Koleji'nden A. Klug ile D.
Caspar'dır. Üzerinde ilk
tespit yapılan virüs ise Polyo
virüsüdür. Rhino 14 virüsü de
Polyo virüsü ile aynı formu
gösterir.
Peki acaba virüsler neden biz
insanların zihnimizde
canlandırmasını bile zorlukla
yapabildiğimiz, böyle altın
orana dayalı özel bir formlara
sahiptirler?
DNA'da Altın Oran
Canlıların tüm fiziksel
özelliklerinin depolandığı
molekül de altın orana
dayandırılmış bir formda
yaratılmıştır. yaşam için
program olan DNA molekülü
altın orana dayanmıştır. DNA
düşey doğrultuda iç içe açılmış
iki sarmaldan oluşur. Bu
sarmallarda her birinin bütün
yuvarlağı içindeki uzunluk 34
angström genişliği 21
angström'dür. (1 angström;
santimetrenin yüz milyonda
biridir) 21 ve 34 art arda gelen
iki Fibonacci sayısıdır
Kar Kristallerinde Altın Oran
Altın oran kristal yapılarda da kendini gösterir. Bunların
çoğu gözümüzle göremeyeceğimiz kadar küçük yapıların
içindedir. Ancak kar kristali üzerindeki altın oranı
gözlerinizle göre bilirsiniz. Kar kristalini oluşturan kısalı
uzunlu dallanmalarda, çeşitli uzantıların oranı hep altın
oranı verir.
Uzayda Altın Oran
• Evrende, yapısında altın
oran barındıran birçok
spiral galaksi bulunur.
Fizikte de Altın Oran....
Fibonacci dizileri ve altın oran
ile fizik biliminin sahasına giren
konularda da karşılaşırız:
"Birbiriyle temas halinde olan iki
cam tabakasının üzerine bir ışık
tutulduğunda, ışığın bir kısmı öte
yana geçer, bir kısmı soğurulur,
geriye kalanı da yansır. Meydana
gelen, bir, 'çoklu yansıma'
olayıdır. Işının tekrar ortaya
çıkmadan önce camın içinde
izlediği yolların sayısı, ışının
maruz kaldığı yansımaların
sayısına bağlıdır. Sonuçta,
tekrar ortaya çıkan ışın
sayılarını belirlediğimizde
bunların Fibonacci sayılarına
uygun olduğunu anlarız."
15)Mimar Sinan: Mimar Sinan'ın da bir çok eserinde bu
altın oran görülmektedir. Mesela Süleymaniye ve
Selimiye Camileri'nin minarelerinde bu oran
görülmektedir.
16- Arılar:
Erkek arılar yalnız anneye sahip babaya sahip
değildirler.
Dişi arılar, anne ve babanın her ikisine de sahiptirler.
Anne -baba
Nine -dede
Büyük nine
/dede
Büyük
büyük nine
/dede
Büyük
büyük
büyük
nine/dede
ERKEK
BAL
ARISI
1
2
3
5
8
DİŞİ BAL
ARISI
2
3
5
8
13
φ
1
Kenarlarının oranı altın orana eşit olan bir dikdörtgene
"altın dikdörtgen" denir. Uzun kenarı 1,618 birim kısa
kenarı 1 birim olan bir dikdörtgen altın dikdörtgendir. Bu
dikdörtgenin kısa kenarının tamamını kenar kabul eden
bir kare ve hemen ardından karenin iki köşesi arasında
bir çeyrek çember çizelim. Kare çizildikten sonra yanda
kalan küçük bir kare ve çeyrek çember çizip bunu asıl
dikdörtgenin içinde kalan tüm dikdörtgenler için yapalım.
Bunu yaptığınızda karşınıza bir sarmal çıkacaktır.
İyi günler dilerim…