August 2017 Istanbul Technical University

August 2017
Istanbul Technical University - Faculty of Science and Letters
Freshman and Sophomore Mathematics Courses (Mat101, 101E, 103, 103E, 104, 104E, 201, 201E, 261,
261E).
The Mathematics Department of ITU provides training to students in their first and second year at the
university via three different mathematics courses. The students arrive at ITU having obtained quite high
entrance examination grades, so the mathematics courses start directly at the Calculus level (no precalculus courses are offered).
There are two sequential calculus courses,
Mat101-1021 course language Turkish (Mat101E-102E course language English) – 5 credits and
Mat103-1042 course language Turkish (Mat103E-104E course language English) – 4 credits.
Each year over 8,300 freshmen attend these courses. Calculus I (both Mat101 and 103) covers the calculus
of single variable functions and differential and integral calculus with applications. Calculus II (both
Mat102 and 104) covers infinite series, calculus of vectors, multivariable functions and multiple integrals.
The two-semester Calculus sequence is mandatory throughout the university with the exception of the
Faculty of Architecture, which requires only the single variable Calculus I. The Calculus sequence is in
general completed in the first year and, for many departments, serves as a prerequisite for other courses.
Starting Fall term 2017, there will be some changes to the Calculus sequence (see Improvements section
below.)
The Differential Equations course Mat201 (course language Turkish), and Mat201E (course language
English), is a required course in the curriculum of all the engineering departments and is offered to
sophomores both Fall and Spring terms, although most departments prefer to take this course in the Fall
to meet their departmental prerequisites. Each year over 2,700 sophomores attend this course. It covers
ordinary differential equations including series methods.
The Linear Algebra course Mat261 (course language Turkish), and Mat261E (course language English), is
a required course in the curriculum of some of the engineering departments and is offered to both
freshmen and sophomores. Some of the departments offer additional MAT coded courses that are not
under the Mathematics Department’s responsibility. Each year over 2,200 students attend this course. It
covers matrices and systems of linear equations, vector spaces, linear transformations and matrix
representations of linear transformations.
With the increasing complexity of engineering problems, the use and the role of mathematics has become
the primary pillar of engineering practice. The fundamental goal of the freshman and sophomore
1
2
See Appendix 1
See Appendix 1
mathematics courses is to help prepare students to enter the world of science and engineering. With the
help of these mathematics courses, students in their first and second years achieve simple mastery of
solution techniques, understanding of mathematical ideas and processes, and efficiency in applying their
understanding to the formation and analysis of mathematical models of physical phenomena and
engineering systems.
Starting Fall term 2017 there will be some changes to the Differential Equations and the Linear Algebra
courses (see Improvements section below.)
Since 2003, the Math Department has given the above courses with parallel sections; students are free to
register for any section of their required course regardless of their department and program. All students
registered in the same course, regardless of course language, take the same midterm and final exam on
the same day (Saturday), and are considered in the same grade distribution. Immediately following the
examination, solutions are posted on the website www.ninova.itu.edu.tr and the lecturers and teaching
assistants (supervised by the lecturers) begin to grade the examination papers. The grades are recorded
and are posted on the department website www.mat.itu.edu.tr
Each semester, a course coordinator is appointed for every course. The course coordinator is responsible
for planning and coordinating the delivery of the course and for ensuring its appropriate assessment
together with the Head of Department, who has the final responsibility. The coordinator is also
responsible for organizing the grading of examination papers.
The Department of Mathematics posts non-graded homework for each course on the website
www.ninova.itu.edu.tr. The preparation of homework that serves to guide the students is the
responsibility of course coordinators and is posted after each chapter.
The lecturer of each course allocates a 2-hour office hour period for student queries that is indicated on
a weekly course schedule hung on his or her door. Teaching assistants do the same.
Each semester an exam committee is appointed to every course consisting of faculty members that are
not assigned to the particular course. The committee assists with determining exam content, writing new
exam questions, and editing exam questions to maintain a high standard of exam quality.
Improvements
Going into effect Fall term 2017, math courses will be changed in line with curricular improvements being
done throughout the university:
The Calculus sequence is now standardized across departments3. This will help with the counting
of courses in the case of transfers between departments.
The Differential Equations and Linear Algebra courses, in an approach closer to that which has
been gaining popularity globally, have been combined into one course, namely Engineering
3
See Appendix 2 &3 – the new course catalogue forms.
Mathematics4. Students, as a result, will be better able to observe the interaction between the
two subjects.
Since 2012, the Mathematics Department has strived to use the ITU Student Information System, Ninova,
more effectively to maintain communication with students, share information, and to increase
coordination and information sharing amongst lecturers offering the same courses. Students can use
Ninova to access course material, homework, past terms’ exam questions and solutions, and exam
locations, along with their exam grades. Lecturers can send group announcements and documents to
students as well.
The past year we have begun to develop and add to the department website as well. Currently, exam
locations and grades are posted on the website. Teachers can access information about their students
and statistics about their courses through the site. Additionally, teachers can see students who have
appealed grades, along with their grades, and make merited changes online during the appropriate
period. Students, then, are able to access the results of their grade appeals online.
The process of exam grade entry was automated during spring term, 2017. Exam papers were
standardized so that grade entry may be done using an optic reader. This offers the advantage of speed
and lessens error. An anticipated change is the ability to digitize graded exams using an optic reader
during the grade entry process. This will make archiving and responding to exam appeals easier.
4
See Appendix 4 – the new course catalogue form.
Appendix 1
Mathematics Department
Mat103-Mat103E-Mat101-Mat101E(Mathematics 1)
Mat104-Mat102-Mat102E(Mathematics 2)
Faculty
IS
Program
104
102
104
201
201
201
102
102
102
102
102
201
201
201
261
201
101E
102E
201
JDF Geodesy and Photogammetry Eng
(GEO Geomatics Eng.)
101
102
201
CEV Environmental Eng.
103
104
201
FIZ Physics Eng.
KIM Chemistry
JEF Geophysical Eng.
JEO Geological Eng.
MD
PET Petroleum and Natural Gas Eng.
MAD Mining Eng.
CHZ Mineral Processing Eng.
INS Civil Eng.
INB
UCK Aeronautical Eng.
UU
UZB Astronautical Eng.
MTO Meteorological Eng.
MK
MAK Mechanical Eng.
IML Manufacturing Eng.
BB
KM
102/104 261
102/104 261
102
261
103
103
104
104
261
201
201
KON Control Eng.
BLG Computer Eng.
101E
281E*
102
201
KMM Chemical Eng.
103
103
103
104
104
104
201E
201
201E
104
104
201E
201E
104
261
ELK Electrical Eng.
MET Meallurgical and Materials Eng.
GEM Naval Architecure and Marine Eng.
DEN Ship Building and Ocean Eng.
EUT Industrial Product Design
ICM Interior Architecture
PEM Landscape Architecture
TEK Textile Eng.
103
103
261
261
4th Semester
261
261
201
201
201
201
201
201
201
201
SBP Urban and Regional Planning
TT
101/103
101/103
101
102E
102E
102E
102E
MIM Architecture
MM
261
281*
281*
281*
281*
TEL Telecommunication Eng.
GID Food Eng.
GD
101
101
101
101
101
261
101E
101E
101E
101E
ELE Electronics Eng.
EE
103
101
103
261
3rd Semester
201E
201E
ISL Managment Science and Eng.
103
103
2nd Semester
104
104
END Industrial Eng.
BIO Molecular Biology and Genetics
FE
1th Semester
Mat 201-Mat201E
(Differential Equations)
Mat261 (Linear Algebra)
261
103E
103E
103E
103E
103E
103
201
Mat281-Mat281E-(Linear Algebra and Applications)course given by the Faculty of Electrical and Electronic Eng
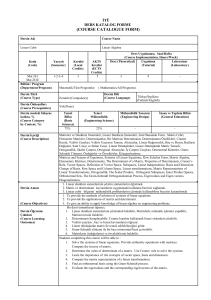
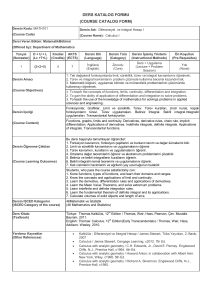
Appendix 2
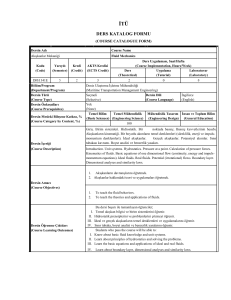
İTÜ
DERS KATALOG FORMU
(COURSE CATALOGUE FORM)
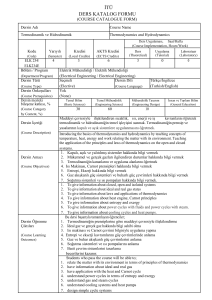
Dersin Adı
Course Name
Matematik I
Mathematics I
Kodu
(Code)
Yarıyılı
(Semester)
Kredisi
(Local
Credits)
Mat 103-103E
1
4
AKTS
Kredisi
(ECTS
Credits)
6*
Bölüm / Program
(Department/Program)
Matematik/Tüm Programlar
Dersin Türü
(Course Type)
Zorunlu (Compulsory)
Dersin Önkoşulları
(Course Prerequisites)
Dersin mesleki bileşene
katkısı, %
(Course Category
by Content, %)
Dersin İçeriği
(Course Description)
Dersin Amacı
(Course Objectives)
Dersin Öğrenme
Çıktıları
(Course Learning
Outcomes)
Ders Uygulaması, Saat/Hafta
(Course Implementation, Hours/Week)
Ders (Theoretical)
Uygulama
Laboratuar
(Tutorial)
(Laboratory)
3
2
-
( Mathematics/All Programs)
İngilizce (English)
Dersin Dili
(Course Language)
Yok(None)
Temel
Bilim
(Basic
Sciences)
100%
Temel
Mühendislik
(Engineering Science)
Mühendislik Tasarım
(Engineering Design)
İnsan ve Toplum Bilim
(General Education)
-
-
Tek Değişkenli Fonksiyonlar, Limit ve Süreklilik, Türev, Türevin Uygulamaları, Eğri Çizimi, Asimptotlar
lar, Integral, İntegral Hesabının Temel Teoremi, İntegralin Uygulamaları, Transandan Fonksiyonlar,
İntegral Teknikleri, Belirsizlik Şekilleri, L’Hopital Kuralı, Genelleştirilmiş İntegraller.
Functions of a Single Variable, Limits and Continuity, Derivatives, Applications of Derivatives, Sketching
Graphs of Functions, Asymptotes, Integration, Fundamental Theorem of Calculus, Applications of
Integrals, Transcendental Functions, Techniques of Integration, Indeterminate Forms, L’Hopital’s Rule,
Improper Integrals.
1. Tek değişkenli fonksiyonlarda limit, süreklilik, türev kavramlarını öğretmek.
2. Türev ve integral kavramlarını uygulamada kullanma becerisi sağlamak.
3. Matematik bilgisini mühendislik problemlerini çözmede kullanabilme becerisi kazandırmak
1. To provide the concepts of functions, limits, continuity, differentiation and integration.
2. To provide the applications of differentiation and integration
3. To give an ability to apply knowledge of mathematics on engineering problems
Bu dersi tamamlayan öğrenci,
I. Tek değişkenli fonksiyonlarda Limit ve süreklilik kavramlarını kullanabilme,
II. Fonksiyonların grafiğinin, asimptot, kritik nokta, azalan/artan ve konkavlığının incelenerek
çizilmesi,
III. Maksimum minimum problemlerinin kurulması ve çözülmesi,
IV. Integral Hesabın Esabı Esas Teoremini kullanarak belirli integral hesabı ve alan hacim , uzunluk
hesabını belirli integral yardımıyla çözebilme,
V. Transandan Fonksiyonlarla işlem yapma ve integral alma tekniklerini uygulama,
VI. Belirsizlik şekilleri ve L’Hopital kuralı yardımıyla limit bulabilme,
VII. Genelleştirimiş integrallerin yakınsaklığı ve ıraksaklığı belirleme,
becerilerini kazanır.
Students completing this course will be able to :
I. Compute the limit of various functions, use the concepts of the continuity, use the rules of
differentiation to differentiate functions.
II. Sketch the graph of a function using asymptotes, critical points and the derivative test for
increasing/decreasing and concavity properties.
III. Set up max/min problems and use differentiation to solve them.
IV. Evaluate integrals by using the Fundamental Theorem of Calculus and apply integration to compute
areas and volumes by slicing, volumes of revolution, arclength.
V. Work with transcendental functions and evaluate integrals using techniques of integration.
VI. Use L'Hospital's rule.
VII. Determine convergence/divergence of improper integrals.
Appendix 2
Ders Kitabı
(Textbook)
Diğer Kaynaklar
Thomas’ Calculus, 10th Edition, G.B Thomas, R. L. Finney, M.D.Weir, F.R.Giordano, AddisonWesley, 2005.
(Other References)
Ödevler ve Projeler
Öğrencilere dersi daha iyi anlamaları amacı ile ödev verilecek ve bu ödevler 1 hafta içinde toplanacaktır.
(Homework & Projects
All homeworks are to be HANDED IN a week after they are assigned. Homeworks may be used as a
source for exams.
Laboratuar Uygulamaları
(Laboratory Work)
Bilgisayar Kullanımı
(Computer Use)
Diğer Uygulamalar
(Other Activities)
Başarı Değerlendirme
Sistemi
(Assessment Criteria)
Faaliyetler
(Activities)
Yıl İçi Sınavları
(Midterm Exams)
Kısa Sınavlar
(Quizzes)
Ödevler
(Homeworks)
Projeler
(Projects)
Dönem Ödevi
(Term Paper)
Laboratuar Uygulaması
(Laboratory Work)
Diğer Uygulamalar
(Other Activities)
Final Sınavı
(Final Exam)
Adedi
(Quantity)
1
Değerlendirmede Katkısı, %
(Effects on Grading, %)
40%
4
-------
1
60%
(*)Zorunlu durumlarda programlar AKTS(ECTS) değerini ± 0,5 aralığında kalmak koşulu ile farklı uygulayabilir.
Appendix 2
DERS PLANI
Hafta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Konular
Limit ve Süreklilik
Limit ve Süreklilik
Türev
Türev
Türevin Uygulamaları
Türevin Uygulamaları
Integral
Integral/ARA SINAV
Integralin Uygulamaları
Integralin Uygulamaları/Transandan Fonksiyonlar
Transandan Fonksiyonlar
Integral Teknikleri
Integral Teknikleri/L’Hopital Kuralı
Genelleştirilmiş İntegraller
Ders
Çıktısı
I
I
I
I
II
II-III
IV
IV
IV
IV-V
V
V
V-VI
VII
COURSE PLAN
Weeks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Topics
Limits and Continuity
Limits and Continuity
Derivatives
Derivatives
Applications of Derivatives
Applications of Derivatives
Integration
Integration/MIDTERM EXAM
Applications of Integrals
Applications of Integrals/Transcendental Functions
Transcendental Functions
Techniques of Integration
Techniques of Integration
Improper integrals
Course
Outcomes
I
I
I
I
II
II-III
IV
IV
IV
IV-V
V
V
V-VI
VII
Appendix 2
Dersin Mühendislik Programıyla İlişkisi
Programın mezuna kazandıracağı bilgi ve beceriler (programa ait çıktılar)
a
b
c
d
e
f
g
h
i
j
k
Katkı
Seviyesi
1 2 3
Matematik, fen bilimleri ve mühendislik bilgisini mühendislik problemlerini çözmede kullanabilme becerisi
Deney tasarlayıp yürütebilme, sonuçlarını analiz edip yorumlama ve modern araç, gereç ve teçhizatı
kullanabilme becerisi
Bir makinayı, parçasını veya prosesi, beklenen performansı, imalat özelliklerini ve ekonomikliği sağlayacak
şekilde seçme, geliştirme ve tasarlama becerisi
Çok disiplinli takımlarda çalışabilme ve/veya liderlik yapma becerisi
Mühendislik problemlerini tanımlama, formüle etme ve çözme becerisi
Mesleki ve etik sorumluluk anlayışına sahip olma
Türkçe ve İngilizce etkin yazılı ve sözlü iletişim kurma becerisi
Mühendisliğinin ulusal ve küresel boyutlardaki etkileri hakkında bilgi sahibi olma ve yorum yapabilme
becerisi
Hayat boyu (Sürekli) eğitimin önemini kavrama ve uygulayabilme becerisi
Mühendisliğinin güncel ve çağdaş konularına ilişkin bilgi sahibi olma
Mühendislik tasarım ve analizlerinde bilgisayar yazılımları gibi modern mühendislik yöntemlerini ve çağdaş
bilgi erişim olanaklarını kullanabilme becerisi
X
X
X
X
X
X
1: Az Katkı, 2. Kısmi Katkı, 3. Tam Katkı
Relationship between the Course and the Engineering Curriculum
Level of
Contribution
1
2
3
Program Outcomes
a
b
c
d
e
f
g
h
i
j
k
An ability to apply knowledge of mathematics, science, and engineering on engineering problems
An ability to design and conduct experiments, as well as to analyze and interpret data and use modern
tools and equipment.
An ability to select, develop and/or design a system, component, or process to meet desired performance,
manufacturing capabilities and economic requirements.
An ability to function on and/or develop leadership in multi-disciplinary teams.
An ability to identify, formulate, and solve engineering problems.
An understanding of professional and ethical responsibility
An ability for effective written and oral communication in Turkish and English.
An ability to understand and comment on the impact of engineering solutions in a national and global
context.
A recognition of the need for, and an ability to engage in life-long learning
A knowledge of contemporary issues in engineering
An ability to use the techniques, skills, and modern engineering tools , such as computer programs,
necessary for engineering design and analysis and use modern information systems
1: Little Contribution, 2. Partial Contribution, 3. Full Contribution
Düzenleyen (Prepared by)
Tarih (Date)
Department of Mathematics
2017
İmza (Signature)
X
X
X
X
X
X
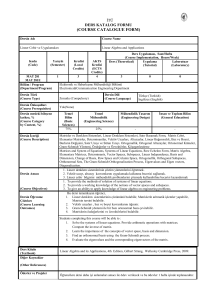
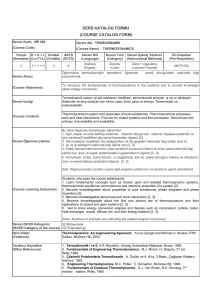
Appendix 3
İTÜ
DERS KATALOG FORMU
(COURSE CATALOGUE FORM)
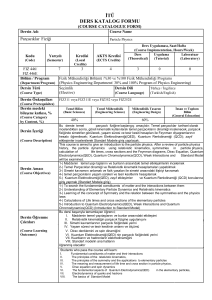
Dersin Adı
Course Name
Matematik II
Mathematics II
Kodu
(Code)
Yarıyılı
(Semester)
Kredisi
(Local
Credits)
Mat 104-104E
2
4
AKTS
Kredisi
(ECTS
Credits)
6,5*
Ders Uygulaması, Saat/Hafta
(Course Implementation, Hours/Week)
Ders (Theoretical)
Uygulama
Laboratuar
(Tutorial)
(Laboratory)
3
2
-
Bölüm / Program
(Department/Program)
Matematik/Tüm Programlar
Dersin Türü
(Course Type)
Zorunlu (Compulsory)
Dersin Önkoşulları
(Course Prerequisites)
MAT103 MIN DD / MAT103E MIN DD/MAT101E MIN DD/MAT 101 MIN DD/ MAT110E MIN
DD/MAT 110 MIN DD
Dersin mesleki bileşene
katkısı, %
(Course Category
by Content, %)
Dersin İçeriği
(Course Description)
Dersin Amacı
(Course Objectives)
Dersin Öğrenme
Çıktıları
(Course Learning
Outcomes)
Temel
Bilim
(Basic
Sciences)
100%
( Mathematics/All Programs)
İngilizce (English)
Dersin Dili
(Course Language)
Temel
Mühendislik
(Engineering Science)
Mühendislik Tasarım
(Engineering Design)
İnsan ve Toplum Bilim
(General Education)
-
-
Sonsuz diziler ve Seriler, Kutupsal Koordinatlar, Uzayda vektörler, Vektör-Değerli Fonksiyonlar, Çok
değişkenli fonksiyonlar ve kısmi türevler, Çok Katlı İntegraller,
Infinite sequences and series, Polar Coordinates, Vectors in Space, Vector-Valued Functions, Multivarible
Functions and Partial Derivatives, Multiple Integrals,
1. Dizilerde, serilerde yakınsaklık kavramlarını ve bunların uygulamalarını öğretmek.
2. Çok değişkenli fonksiyonlarda kısmi türev ve integral kavramlarını kullanma becerisi sağlamak.
3. Matematik bilgisini mühendislik problemlerini çözmede kullanabilme becerisi kazandırmak
1. To provide the concepts and applications of the convergence of sequences and infinite series.
2. To provide the applications of partial differentiation and multiple integrals.
3. To give an ability to apply knowledge of mathematics on engineering problems
Bu dersi tamamlayan öğrenci,
I. Dizilerin ve serilerin yakınsaklığını; kuvvet serilerinin yakınsaklık yarıçapını bulabilme,
II. Bir fonksiyonu Taylor Serisine açabilme ve yapılan hata payını bulabilme,
III. Üç boyutlu uzayda vektörlerin, vektörel ve skaler çarpımını hesaplayabilme; doğru, düzlem ve
kuadrik yüzey denklemlerini yazabilme,
IV. Vektör değerli fonksiyonlar için limit, süreklilik, ve integral kavramlarını kullanabilme,
V. Çok değişkenli fonksiyonlarda limit, süreklilik kavramlarını kullanabilme; kısmi türev
hesaplayabilme; teğet düzlem, doğrultuya göre türev ve gradiyent bulabilme; ekstremum
problemlerini ikinci türev testi ve Lagrange çarpan metodu ile çözebilme,
VI. Çok katlı integralleri çözebilme; alan ve hacim hesabında çok katlı integralleri kullanabilme,
Students completing this course will be able to:
I. Compute limits of sequences and series; determine the convergence of the series and the radius of
convergence of power series.
II. Represent a known function as a Taylor series; approximate a known function with a Taylor
polynomial and determine the error involved.
III. Compute the standard representation of a vector in 3-space, compute the dot product and cross
product of vectors; write equations of lines, planes and quadric surfaces in 3-space.
IV. Use the concepts of continuity, differentiation, and integration of vector-valued functions.
V. Understand the multivariable functions, analyze limits, determine continuity, and compute partial
derivatives of them; find tangent planes, directional derivatives, gradients; apply the second partials
test, and Lagrange multipliers to approximate and solve optimization problems.
VI. Compute multiple integrals over rectangular regions, non-rectangular regions, and in other
coordinate systems; apply multiple integrals in problem situations involving area, volume, surface
area etc.
Appendix 3
Ders Kitabı
(Textbook)
Diğer Kaynaklar
Thomas’ Calculus, 10th Edition, G.B Thomas, R. L. Finney, M.D. Weir, F.R.Giordano, AddisonWesley, 2005.
(Other References)
Ödevler ve Projeler
Öğrencilere dersi daha iyi anlamaları amacı ile ödev verilecek ve bu ödevler 1 hafta içinde toplanacaktır.
(Homework & Projects
All homeworks are to be HANDED IN a week after they are assigned. Homeworks may be used as a
source for exams.
Laboratuar Uygulamaları
(Laboratory Work)
Bilgisayar Kullanımı
(Computer Use)
Diğer Uygulamalar
(Other Activities)
Başarı Değerlendirme
Sistemi
(Assessment Criteria)
Faaliyetler
(Activities)
Yıl İçi Sınavları
(Midterm Exams)
Kısa Sınavlar
(Quizzes)
Ödevler
(Homeworks)
Projeler
(Projects)
Dönem Ödevi
(Term Paper)
Laboratuar Uygulaması
(Laboratory Work)
Diğer Uygulamalar
(Other Activities)
Final Sınavı
(Final Exam)
Adedi
(Quantity)
1
Değerlendirmede Katkısı, %
(Effects on Grading, %)
40%
4
-------
1
60%
(*)Zorunlu durumlarda programlar AKTS(ECTS) değerini ± 0,5 aralığında kalmak koşulu ile farklı uygulayabilir.
Appendix 3
DERS PLANI
Hafta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Konular
Kutupsal Koordinatlar
Kutupsal Koordinatlar/ Uzayda Vektörler
Uzayda Vektörler
Vektör Değerli Fonksiyonlar
Çok Değişkenli Fonksiyonlar ve kısmi türevler
Çok Değişkenli Fonksiyonlar ve kısmi türevler
Çok Değişkenli Fonksiyonlar ve kısmi türevler
Çok Katlı Integraller /Arasınav
Çok Katlı İntegraller
Çok Katlı İntegraller
Sayı Dizileri
Seriler
Seriler
Seriler
Ders
Çıktısı
VI
VI-III
III
IV
V
V
V
V
VI
VI
I
I
I
I-II
COURSE PLAN
Weeks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Topics
Polar Coordinates
Polar Coordinates/Vectors in space
Vectors in space
Vector valued functions
Multivariable Functions and Partial Derivatives
Multivariable Functions and Partial Derivatives
Multivariable Functions and Partial Derivatives
Multiple Integrals//Midterm
Multiple Integrals
Multiple Integrals
Sequences of numbers
Infinite Series
Infinite Series
Infinite Series
Course
Outcomes
VI
VI-III
III
IV
V
V
V
V
VI
VI
I
I
I
I-II
Appendix 3
Dersin Mühendislik Programıyla İlişkisi
Programın mezuna kazandıracağı bilgi ve beceriler (programa ait çıktılar)
a
b
c
d
e
f
g
h
i
j
k
Katkı
Seviyesi
1 2 3
Matematik, fen bilimleri ve mühendislik bilgisini mühendislik problemlerini çözmede kullanabilme becerisi
Deney tasarlayıp yürütebilme, sonuçlarını analiz edip yorumlama ve modern araç, gereç ve teçhizatı
kullanabilme becerisi
Bir makinayı, parçasını veya prosesi, beklenen performansı, imalat özelliklerini ve ekonomikliği sağlayacak
şekilde seçme, geliştirme ve tasarlama becerisi
Çok disiplinli takımlarda çalışabilme ve/veya liderlik yapma becerisi
Mühendislik problemlerini tanımlama, formüle etme ve çözme becerisi
Mesleki ve etik sorumluluk anlayışına sahip olma
Türkçe ve İngilizce etkin yazılı ve sözlü iletişim kurma becerisi
Mühendisliğinin ulusal ve küresel boyutlardaki etkileri hakkında bilgi sahibi olma ve yorum yapabilme
becerisi
Hayat boyu (Sürekli) eğitimin önemini kavrama ve uygulayabilme becerisi
Mühendisliğinin güncel ve çağdaş konularına ilişkin bilgi sahibi olma
Mühendislik tasarım ve analizlerinde bilgisayar yazılımları gibi modern mühendislik yöntemlerini ve çağdaş
bilgi erişim olanaklarını kullanabilme becerisi
X
X
X
X
X
X
1: Az Katkı, 2. Kısmi Katkı, 3. Tam Katkı
Relationship between the Course and the Engineering Curriculum
Level of
Contribution
1
2
3
Program Outcomes
a
b
c
d
e
f
g
h
i
j
k
An ability to apply knowledge of mathematics, science, and engineering on engineering problems
An ability to design and conduct experiments, as well as to analyze and interpret data and use modern
tools and equipment.
An ability to select, develop and/or design a system, component, or process to meet desired performance,
manufacturing capabilities and economic requirements.
An ability to function on and/or develop leadership in multi-disciplinary teams.
An ability to identify, formulate, and solve engineering problems.
An understanding of professional and ethical responsibility
An ability for effective written and oral communication in Turkish and English.
An ability to understand and comment on the impact of engineering solutions in a national and global
context.
A recognition of the need for, and an ability to engage in life-long learning
A knowledge of contemporary issues in engineering
An ability to use the techniques, skills, and modern engineering tools , such as computer programs,
necessary for engineering design and analysis and use modern information systems
1: Little Contribution, 2. Partial Contribution, 3. Full Contribution
Düzenleyen (Prepared by)
Tarih (Date)
Department of Mathematics
2017
İmza (Signature)
X
X
X
X
X
X
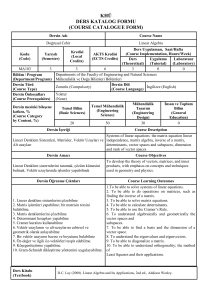
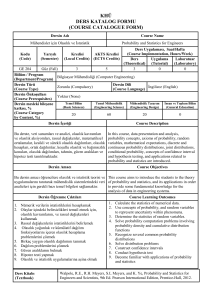
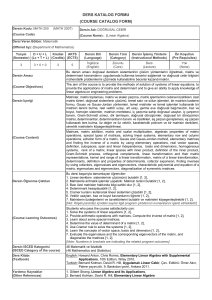
Appendix 4
DERS KATALOG FORMU
( COURSE CATALOGUE FORM)
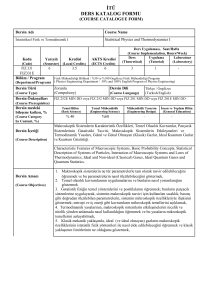
Dersin Adı
Mühendislik Matematiği
Course Name
Engineering Mathematics
Kodu
(Code)
Yarıyılı
(Semester)
Kredisi
(Local
Credits)
Mat 210-210E
3-4
4
Bölüm / Program
(Department/Program)
Dersin Türü
(Course Type)
Dersin Önkoşulları
(Course Prerequisites)
Dersin mesleki bileşene
katkısı, %
(Course Category
by Content, %)
Dersin İçeriği
(Course Description)
Dersin Amacı
(Course Objectives)
Dersin Öğrenme
Çıktıları
(Course Learning
Outcomes)
AKTS
Kredisi
(ECTS
Credits)
6*
Matematik/Tüm Programlar
Zorunlu (Compulsory)
Ders Uygulaması, Saat/Hafta
(Course Implementation, Hours/Week)
Ders (Theoretical)
Uygulama
Laboratuar
(Tutorial)
(Laboratory)
4
-
( Mathematics/All Programs)
Ingilizce(English)
Dersin Dili
(Course Language)
MAT 102 MIN DD/ MAT 102E MIN DD/ MAT 104 MIN DD/ MAT 104E MIN DD/MAT120E MIN DD/MAT 120
MIN DD
Temel
Bilim
(Basic
Sciences)
40%
Temel
Mühendislik
(Engineering Science)
Mühendislik Tasarım
(Engineering Design)
İnsan ve Toplum Bilim
(General Education)
60%
-
-
Matrisler ve Lineer Denklem Sistemleri, Vektör uzayları, Özdeğerler ve Özvektörler,Birinci Mertebeden Diferansiyel
Denklemler, Yüksek Mertebeden Lineer Diferansiyel Denklemler, Laplace Dönüşümleri, Birinci Mertebeden Lineer
Diferensiyel Denklem Sistemleri
Matrices and System of Equations, Systems of Linear Equations, Vector Spaces, Eigenvalues and Eigenvectors, First
Order Differential Equations, , Higher Order Linear Equations,The Laplace Transform, Systems of First Order Linear
Differential Equations
1. Lineer denklem sistemlerinin çözüm yöntemlerini, matris ve determinant kavramlarını öğreterek
mühendislik problemlerine uygulama becerisi sağlamak.
2. Diferansiyel denklemleri anlamak, kurmak, çözmek ve yorumlamak için gerekli olan temel
kavramları tanıtmak ve çeşitli tipte diferansiyel denklem çözme teknikleri öğreterek mühendislik
problemlerinin çözümünde kullanma becerisi sağlamak
3. Matematik bilgisini temel bilim ve mühendislik problemlerini çözmede kullanabilme becerisi
kazandırmak
1. To teach the methods of solution of systems of linear equations an applications of matrix and
determinant to provide skills in application to engineering problems.
2. To introduce the basic concepts necessary to understand, construct, solve and interpret differential
equations, to teach methods to solve differential equations of various types to provide skills in
application to engineering problems.
3. To give an the ability to use mathematics knowledge to solve basic science and engineering
problems
Bu dersi tamamlayan öğrenci,
I.
Lineer denklem sistemlerinin çözümünü bulabilir, Matrislerle aritmatik işlemler yapabilir,
Matrisin tersini bulabilir.; determinantı hesaplayabilir ve Cramer kuralını kullanarak lineer
sistemleri çözebilir
II.
Vektör uzayları , baz ve boyut kavramlarını öğrenir. Lineer dönüşümün matris ile temsil
edilebileceğini görür. ve matrislerin özdeğerlerini ve özvektörlerini bulabilir
III.
Diferansiyel denklemleri belli özelliklerine göre sınıflandırabilir
IV.
Birinci mertebeden lineer ve belirli tipte lineer olmayan diferansiyel denklemleri çözer,
çözümleri yorumlar ve lineer denklem çözümleri için varlık ve teklik koşullarını anlar
V.
Yüksek mertebeden sabit katsayılı lineer denklemler için çözüm bulur , lineer bağımsız
çözümlerden tüm çözümleri türetebilir ,Laplace dönüşümü kullanarak başlangıç değer
problemleri çözebilir ve Lineer Diferensiyel denklem sistemlerini lineer cebir metodlarıyla
çözebilir
Students completing this course will be able to:
I.
Solve the systems of linear equations., provide arithmetic operations with matrices,
compute the inverse of matrix, determine the value of determinant of a matrix and use Cramer
rule to solve the systems
II.
Learn the importance of the concepts of vector space, basis and dimension, compute the matrix
representation of a linear transformation, and evaluate the eigenvalues and the corresponding
eigenvectors of the matrix.
III.
Classify differential equations according to certain features
IV.
Solve first order linear equations and nonlinear equations of certain types , interpret the solutions
and understand the conditions for the existence and uniqueness of solutions for linear differential
equations
V.
Solve higher order linear differential equations with constant coefficients and construct all
solutions from the linearly independent solutions; solve initial value problems using the Laplace
transform and solve systems of linear differential equations with methods from linear algebra.
Appendix 4
Ders Kitabı
(Textbook)
Diğer Kaynaklar
Differential Equations &Linear Algebra Third Edition Edition, C.Henry Edwards ; David E. Penney
Pearson İnternational Education International,2011.
(Other References)
Ödevler ve Projeler
Öğrencilerin çalışmalarına rehberlik etmesi amacıyla 5 çalışma kağıdı dağıtılacaktır.
(Homework & Projects
There will be 5 worksheets in order to guide the students with their studies.
Laboratuar Uygulamaları
(Laboratory Work)
Bilgisayar Kullanımı
(Computer Use)
Diğer Uygulamalar
(Other Activities)
Başarı Değerlendirme
Sistemi
(Assessment Criteria)
Faaliyetler
(Activities)
Yıl İçi Sınavları
(Midterm Exams)
Kısa Sınavlar
(Quizzes)
Ödevler
(Homeworks)
Projeler
(Projects)
Dönem Ödevi
(Term Paper)
Laboratuar Uygulaması
(Laboratory Work)
Diğer Uygulamalar
(Other Activities)
Final Sınavı
(Final Exam)
Adedi
(Quantity)
1
Değerlendirmede Katkısı, %
(Effects on Grading, %)
40%
1
60%
(*)Zorunlu durumlarda programlar AKTS(ECTS) değerini ± 0,5 aralığında kalmak koşulu ile farklı uygulayabilir.
Appendix 4
DERS PLANI
Hafta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Konular
Birinci Mertebeden Diferansiyel Denklemler
Birinci Mertebeden Diferansiyel Denklemler
Lineer Denklemler ve Matrisler
Lineer Denklemler ve Matrisler
Vektör Uzayları
Vektör Uzayları
Yüksek Mertebeden Diferansiyel Denklemler
Yüksek Mertebeden Diferansiyel Denklemler ARA SINAV
Özdeğerler ve Özvektörler
Özdeğerler ve Özvektörler
Lineer Diferensiyel Denklem Sistemleri
Lineer Diferensiyel Denklem Sistemleri
Laplace Dönüşümü
Laplace Dönüşümü
Ders
Çıktısı
III-IV
IV
I
I
II
II
V
V
II
II
IV-V
IV-V
V
V
COURSE PLAN
Weeks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Topics
First Order Differential Equations
First Order Differential Equations
Matrices and Systems of Equations
Matrices and Systems of Equations
Vector Space
Vector Spaces
Higher Order Differential Equations
Higher Order Differential Equations
Eigenvalues, Eigenvectors
Eigenvalues, Eigenvectors
Linear Systems of Differential Equations
Linear Systems of Differential Equations
The Laplace Transform
The Laplace Transfor
Course
Outcomes
III-IV
IV
I
I
II
II
V
V
II
II
IV-V
IV-V
V
V
Appendix 4
Dersin Mühendislik Programıyla İlişkisi
Programın mezuna kazandıracağı bilgi ve beceriler (programa ait çıktılar)
a
b
c
d
e
f
g
h
i
j
k
Katkı
Seviyesi
1 2 3
Matematik, fen bilimleri ve mühendislik bilgisini mühendislik problemlerini çözmede kullanabilme becerisi
Deney tasarlayıp yürütebilme, sonuçlarını analiz edip yorumlama ve modern araç, gereç ve teçhizatı
kullanabilme becerisi
Bir makinayı, parçasını veya prosesi, beklenen performansı, imalat özelliklerini ve ekonomikliği sağlayacak
şekilde seçme, geliştirme ve tasarlama becerisi
Çok disiplinli takımlarda çalışabilme ve/veya liderlik yapma becerisi
Mühendislik problemlerini tanımlama, formüle etme ve çözme becerisi
Mesleki ve etik sorumluluk anlayışına sahip olma
Türkçe ve İngilizce etkin yazılı ve sözlü iletişim kurma becerisi
Mühendisliğinin ulusal ve küresel boyutlardaki etkileri hakkında bilgi sahibi olma ve yorum yapabilme
becerisi
Hayat boyu (Sürekli) eğitimin önemini kavrama ve uygulayabilme becerisi
Mühendisliğinin güncel ve çağdaş konularına ilişkin bilgi sahibi olma
Mühendislik tasarım ve analizlerinde bilgisayar yazılımları gibi modern mühendislik yöntemlerini ve çağdaş
bilgi erişim olanaklarını kullanabilme becerisi
X
X
X
X
X
X
1: Az Katkı, 2. Kısmi Katkı, 3. Tam Katkı
Relationship between the Course and the Engineering Curriculum
Level of
Contribution
1
2
3
Program Outcomes
a
b
c
d
e
f
g
h
i
j
k
An ability to apply knowledge of mathematics, science, and engineering on engineering problems
An ability to design and conduct experiments, as well as to analyze and interpret data and use modern
tools and equipment.
An ability to select, develop and/or design a system, component, or process to meet desired performance,
manufacturing capabilities and economic requirements.
An ability to function on and/or develop leadership in multi-disciplinary teams.
An ability to identify, formulate, and solve engineering problems.
An understanding of professional and ethical responsibility
An ability for effective written and oral communication in Turkish and English.
An ability to understand and comment on the impact of engineering solutions in a national and global
context.
A recognition of the need for, and an ability to engage in life-long learning
A knowledge of contemporary issues in engineering
An ability to use the techniques, skills, and modern engineering tools , such as computer programs,
necessary for engineering design and analysis and use modern information systems
1: Little Contribution, 2. Partial Contribution, 3. Full Contribution
Düzenleyen (Prepared by)
Department of Mathematics
Tarih (Date)
2017
İmza (Signature)
X
X
X
X
X
X