9. Sınıf Matematik
4. Bölüm: Üçgenler - I
Konu Anlatım Föyleri
A
NELER ÖĞRENECEĞİZ (KAZANIMLAR)
Üçgeni tanımlar, temel ve yardımcı elemanlarını
öğrenir.
Üçgende açı bağıntılarını öğrenir.
B
S
3.
_
G
D
=
Üçgen çeşitlerini kenar ve açılarına göre sınıflar.
E
F
=
2.
|AD|=Va , |BE|=Vb , |CF|=Vc
G noktası ABC üçgeninin
ağırlık merkezidir.
S
1.
_
C
2. Açıortay
ÜÇGEN TANIMI VE TEMEL ELEMANLARI
Bir üçgenin bir açısını iki eşit parçaya bölen ışının, köşe ile
karşı kenar arasında kalan parçasına, üçgenin o köşesine ait
açıortayı denir.
Tanım
Doğrusal olmayan üç noktayı birleştiren doğru parçalarının
birleşimine üçgen denir.
A
m(BAN)=m(NAC) olduğundan
[AN], A açısına ait iç açıortaydır.
A
[AB] U [BC] U [AC] = ABC dir.
nA
N
B
a
B
BAC, ABC ve ACB açılarına üçgenin iç açıları denir.
İç açıların bütünleri olan açılara dış açılar denir.
Üçgenin kenarlarına ve açılarına temel elemanlar denir.
Bir üçgen bulunduğu düzlemi; üçgenin kendisi, iç bölgesi
ve dış bölgesi olmak üzere üç bölgeye ayırır.
Bir üçgenin dış açılarının açıortaylarına dış açıortay denir.
NAMIK KARAYANIK
|AB|=c, |BC|=a, |AC|=b uzunluklarına üçgenin kenar
uzunlukları denir.
ANAHTAR BİLGİ
Bir üçgenin bir köşesindeki açıya ait iç
açıortay ile dış açıortay arasındaki açı 900 dir.
A _y
_
x
x y
A
Kendisi
Dış bölge
İç bölge
B
ABC üçgeninde [AE] ⊥ [AD] dir.
2x + 2y = 1800
2(x + y) = 1800
x + y = 900
C
B
ÜÇGENİN YARDIMCI ELEMANLARI
D
3. Yükseklik
Bir üçgenin bir köşesini karşısındaki kenarın orta noktası
ile birleştiren doğru parçasına üçgenin o kenarına ait
kenarortayı denir.
A
Bir üçgenin bir köşesinden karşı kenar doğrusuna indirilen
dikmenin, karşı kenarı kestiği nokta ile köşeyi birleştiren
doğru parçasına, üçgenin o kenarına ait yüksekliği denir.
|BD|=|DC| olduğundan
[AD], [BC] kenarının
kenarortayıdır.
|AD|= Va : a kenarına ait
kenarortay uzunluğudur.
va
=
=
D
C
E
1. Kenarortay
B
C
ABC üçgeninin A, B ve C açılarına ait iç açıortaylarının
uzunlukları sırasıyla nA , nB ve nC ile gösterilir.
C
A, B, C noktalarına üçgenin köşeleri, [AB], [BC], [AC]
doğru parçalarına üçgenin kenarları denir.
E
|AN|= nA : A açısına ait iç
açıortay uzunluğudur.
b
c
A
A
|AD|=ha : a kenarına ait
yükseklik uzunluğudur.
ha
ABC üçgeninin a, b ve c kenarına ait kenarortaylarının uzunlukları
sırasıyla Va , Vb ve Vc ile gösterilir.
B
Bir üçgenin üç kenarortayı üçgenin içinde bir noktada kesişirler.
Bu noktaya üçgenin ağırlık merkezi denir.
D
[AD] ⊥ BC dir.
ha
C
C
D
B
C
ABC üçgeninin a, b ve c kenarına ait yüksekliklerinin uzunlukları
sırasıyla ha , hb ve hc ile gösterilir.
1
9. Sınıf Matematik
4. Bölüm: Üçgenler - I
Konu Anlatım Föyleri
Bir üçgenin üç yüksekliği bir noktada kesişir. Bu noktaya
üçgenin diklik merkezi denir.
ÜÇGENDE AÇILAR
Teorem 1:
A
A
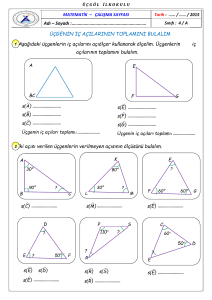
Bir üçgenin iç açılarının ölçüleri toplamı 1800 dir.
A
ABC üçgeninde m(A) = x , m(B) = y , m(C) = z
A
olmak üzere ;
x
K
B
B
C
B
x+y+z=1800 dir.
C
C
K
ABC dar açılı üçgen
K: Diklik merkezi
ABC dik üçgen
B: Diklik merkezi
y
ABC geniş açılı üçgen
K: Diklik merkezi
z
B
C
İspat:
E
F
A
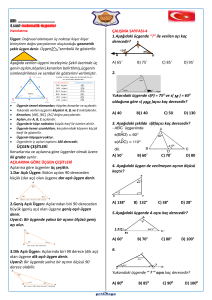
Üçgen Çeşitleri
y
x
z
A) Kenarlarına Göre Üçgen Çeşitleri
y
A
b
c
B
a
A noktasından geçen EF // [BC] çizelim.
C
m(B)=m(EAB)=y
(iç ters açılar)
m(C)=m(FAC)=z
(iç ters açılar)
A
2. İkizkenar Üçgen:
Herhangi iki kenar uzunluğu
birbirine eşit olan üçgene denir.
|AB|=|AC|=b
b
b
a
B
C
a≠b≠c
C
NAMIK KARAYANIK
1. Çeşitkenar Üçgen:
Üç kenar uzunluğu birbirinden
farklı olan üçgene denir.
z
B
EAF doğru açı olduğundan, x+y+z=1800 dir.
Teorem 2:
A
3. Eşkenar Üçgen:
Üç kenar uzunluğu birbirine
eşit olan üçgene denir.
Bir üçgende, bir dış açının ölçüsü kendisine
komşu olmayan iki iç açının ölçüleri toplamına eşittir.
|AB|=|BC|=|AC|=a
a
a
m(PAC)=m(B) + m(C) dir.
B
a
C
m(PAC)= y + z dir.
B) Açılarına Göre Üçgen Çeşitleri
1. Dar Açılı Üçgen:
Üç açısının ölçüsü de 900 den
küçük olan üçgene denir.
2. Dik Açılı Üçgen:
Bir açısının ölçüsü 900 ye
eşit olan üçgene denir
A
x<900
x
y<900
y
B
C
İspat:
A
P
m(B)=900
[AE // [BC] çizelim.
A
E
m(PAE) = m(B) = y
C
B
3. Geniş Açılı Üçgen:
Bir açısının ölçüsü 900 den
büyük olan üçgene denir.
z<900
z
(yöndeş açılar) .... 1
A
m(EAC) = m(C) = z
m(B)>900
z
C
B
(iç ters açılar)
C
1 ve 2 den
2
m(PAC) = y + z dir.
.... 2
9. Sınıf Matematik
Teorem 3:
4. Bölüm: Üçgenler - I
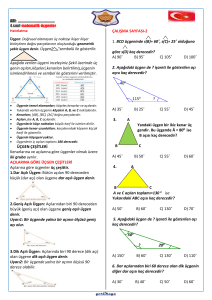
ÜÇGENDE AÇI ÖZELLİKLERİ
Bir üçgenin dış açılarının ölçüleri toplamı
3600 dir.
a
A
A
x
a + b + c = 3600 dir.
b
ABC üçgeninde [BE ve [CE
sırasıyla B ve C açılarının
iç açıortayları olmak üzere;
Özellik 1
ABC üçgeninde A, B, C açılarının dış açılarının ölçüleri
sırasıyla a, b, c olmak üzere ;
P
Konu Anlatım Föyleri
y
z
B
C
c
a
m(BEC) = 900 +
E
x = 900 +
m(A)
2
dir.
a
2
x
İspat:
x + a = 1800
y + b = 1800
z + c = 1800
P
a
A
x
B
C
Özellik 2
ABC üçgeninde [BE] ve [CE] sırasıyla B ve
C açılarının dış açıortayları olmak üzere;
A
eşitlikleri taraf tarafa
toplanırsa,
b
y
z
B
a
C
m(BEC) = 900 -
B
c
C
x = 900 -
m(A)
2
dir.
a
2
a + b + c = 5400 - 1800 ve a + b + c = 3600 bulunur.
ÖRNEK 1:
A
ABC üçgeninde verilenlere
göre A açısının ölçüsü kaç
derecedir?
2x
NAMIK KARAYANIK
x+y+z+a+b+c = 5400 Buradan 1800 + a+b+c = 5400
x
E
Özellik 3
ABC üçgeninde [BE, B açısının iç açıortayı;
[CE, C açısının dış açı ortayı olmak üzere ;
E
A
5x-30
4x+180
B
x
2x
m(BEC) =
C
m(A)
2
ÇÖZÜM:
ABC üçgeninde iç açılar toplamından,
2x + 5x-3 + 4x+18 = 180
11x + 15 =180
11x = 165
x = 15 dir. O halde m(A) = 2.15 = 300 bulunur.
ÖRNEK 2:
A
650
B
C
m(E) = x ise m(A) = 2x tir.
ABC üçgeninde
verilenlere göre,
Özellik 4
Bir üçgenin bir iç açıortayı ile iki dış açı
ortayı bir noktada kesişirler.
m(C) kaç derecedir?
A
5x-50
D
B
K
3x-200
C
ÇÖZÜM: 65 + 3x-20 = 5x-5 ( iki iç bir dış)
2x = 50 ise x = 25 m(C) = 3.25-20 = 550 dir.
B
3
C
dir.
9. Sınıf Matematik
4. Bölüm: Üçgenler - I
Konu Anlatım Föyleri
ÖRNEK 3:
SIRA SENDE GÖR VE UYGULA
A
ÖRNEK 4:
C
500
D
B
D
E
Yandaki şekilde
verilenlere göre,
x açısı kaç derecedir?
x
300
_
x
B
_
C
A
ÖRNEK 5:
Şekilde verilenlere göre,
Yandaki şekilde verilen
x, y, z açı ölçülerini
küçükten büyüğe doğru
sıralayınız.
A
m(BEC) = x açısı kaç derecedir?
x
ÇÖZÜM: [AD] dış aşıortaydır. Buna göre,
D
z
m(A) = 800 , m(B) = 700 dir.
E
y
50
A
800
0
B
500
ÖRNEK 6:
NAMIK KARAYANIK
D
E
300
B
_
1150
350
350
C
_
C
A
Yandaki şekilde
verilenlere göre,
x açısı kaç derecedir?
720
O halde m(BEC) = 80 + 35 =
1150
B
dir.
D
x
E
C
ÖRNEK 7:
ANAHTAR BİLGİ
Bir üçgenin üç iç açıortayı üçgenin içinde bir
noktada kesişirler bu noktaya üçgenin iç teğet çemberinin merkezi denir.
3x
Bir üçgenin iki dış açıortayı ile bir iç açıortayı
üçgenin dışında bir noktada kesişirler bu noktaya üçgenin dış teğet çemberinin merkezi
denir.
C
ÖRNEK 8:
A
x
K
E
F
D
530
A
E
I
_
500
B
A
B
ABC üçgeninde verilen
açı ölçülerine göre,
BAC açısının ölçüsü
kaç derecedir?
A 2x+300
_
D
=
=
C
I noktası üçgenin iç teğet
çemberinin merkezidir.
B
C
B
K noktası üçgenin dış teğet
çemberinin merkezidir.
C
Yukarıdaki şekilde verilenlere göre, x kaç derecedir?
4