FAKÜLTE ve PROGRAM: MÜHENDİSLİK FAKÜLTESİ

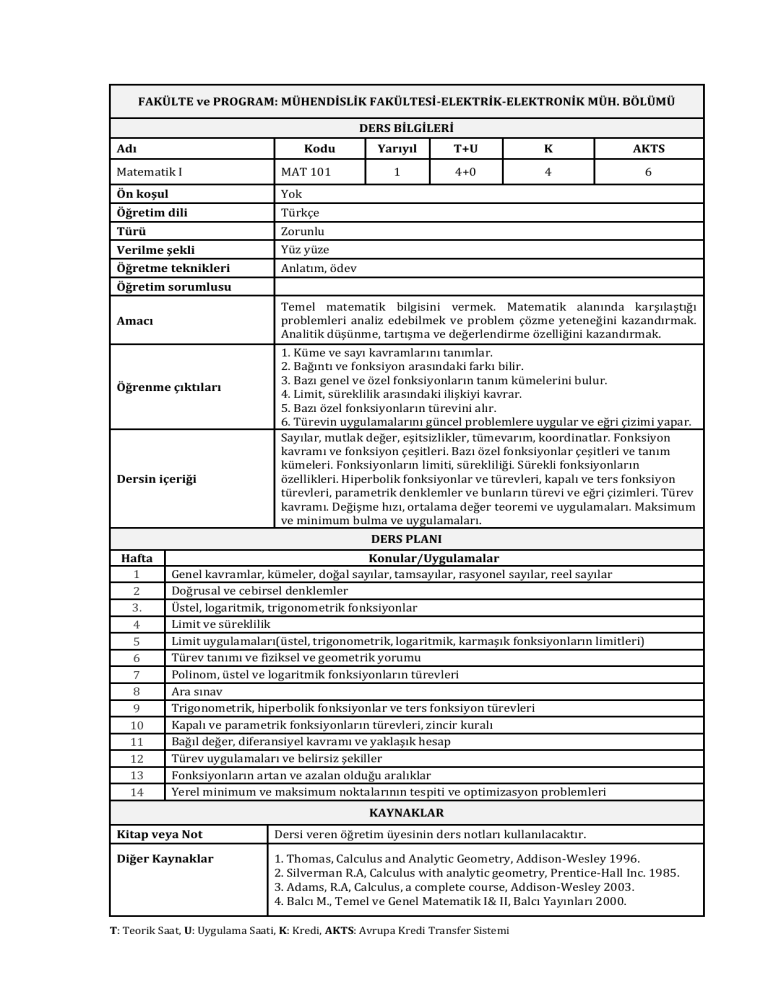
FAKÜLTE ve PROGRAM: MÜHENDİSLİK FAKÜLTESİ-ELEKTRİK-ELEKTRONİK MÜH. BÖLÜMÜ
DERS BİLGİLERİ
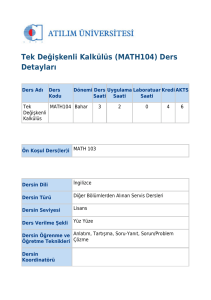
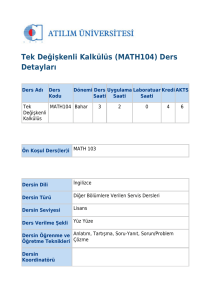
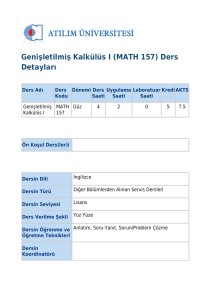
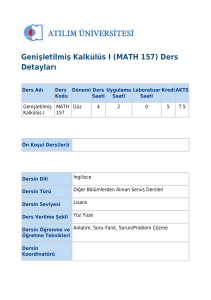
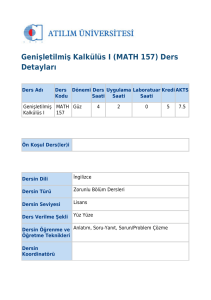
Adı
Kodu
Matematik I
MAT 101
Ön koşul
Yok
Öğretim dili
Türkçe
Türü
Zorunlu
Verilme şekli
Yüz yüze
Öğretme teknikleri
Anlatım, ödev
Yarıyıl
T+U
K
AKTS
1
4+0
4
6
Öğretim sorumlusu
Temel matematik bilgisini vermek. Matematik alanında karşılaştığı
problemleri analiz edebilmek ve problem çözme yeteneğini kazandırmak.
Analitik düşünme, tartışma ve değerlendirme özelliğini kazandırmak.
Amacı
Öğrenme çıktıları
Dersin içeriği
1. Küme ve sayı kavramlarını tanımlar.
2. Bağıntı ve fonksiyon arasındaki farkı bilir.
3. Bazı genel ve özel fonksiyonların tanım kümelerini bulur.
4. Limit, süreklilik arasındaki ilişkiyi kavrar.
5. Bazı özel fonksiyonların türevini alır.
6. Türevin uygulamalarını güncel problemlere uygular ve eğri çizimi yapar.
Sayılar, mutlak değer, eşitsizlikler, tümevarım, koordinatlar. Fonksiyon
kavramı ve fonksiyon çeşitleri. Bazı özel fonksiyonlar çeşitleri ve tanım
kümeleri. Fonksiyonların limiti, sürekliliği. Sürekli fonksiyonların
özellikleri. Hiperbolik fonksiyonlar ve türevleri, kapalı ve ters fonksiyon
türevleri, parametrik denklemler ve bunların türevi ve eğri çizimleri. Türev
kavramı. Değişme hızı, ortalama değer teoremi ve uygulamaları. Maksimum
ve minimum bulma ve uygulamaları.
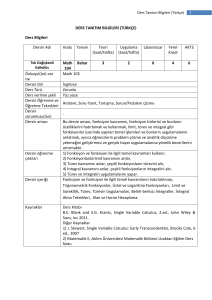
DERS PLANI
Hafta
1
2
3.
4
5
6
7
8
9
10
11
12
13
14
Konular/Uygulamalar
Genel kavramlar, kümeler, doğal sayılar, tamsayılar, rasyonel sayılar, reel sayılar
Doğrusal ve cebirsel denklemler
Üstel, logaritmik, trigonometrik fonksiyonlar
Limit ve süreklilik
Limit uygulamaları(üstel, trigonometrik, logaritmik, karmaşık fonksiyonların limitleri)
Türev tanımı ve fiziksel ve geometrik yorumu
Polinom, üstel ve logaritmik fonksiyonların türevleri
Ara sınav
Trigonometrik, hiperbolik fonksiyonlar ve ters fonksiyon türevleri
Kapalı ve parametrik fonksiyonların türevleri, zincir kuralı
Bağıl değer, diferansiyel kavramı ve yaklaşık hesap
Türev uygulamaları ve belirsiz şekiller
Fonksiyonların artan ve azalan olduğu aralıklar
Yerel minimum ve maksimum noktalarının tespiti ve optimizasyon problemleri
KAYNAKLAR
Kitap veya Not
Dersi veren öğretim üyesinin ders notları kullanılacaktır.
Diğer Kaynaklar
1. Thomas, Calculus and Analytic Geometry, Addison-Wesley 1996.
2. Silverman R.A, Calculus with analytic geometry, Prentice-Hall Inc. 1985.
3. Adams, R.A, Calculus, a complete course, Addison-Wesley 2003.
4. Balcı M., Temel ve Genel Matematik I& II, Balcı Yayınları 2000.
T: Teorik Saat, U: Uygulama Saati, K: Kredi, AKTS: Avrupa Kredi Transfer Sistemi
DEĞERLENDİRME SİSTEMİ
Etkinlik Türleri
Katkı Yüzdesi
40
Ara Sınav
60
Yarıyıl Sonu Sınavı
100
Toplam
PROGRAM ÇIKTILARINA KATKISI
Katkı Düzeyi
No
1
2
3
4
Program Çıktıları
Sistemleri analiz etme ve tasarlama yeteneği ve becerisi kazandırmak
6
Kuramsal bilgileri laboratuvar ve proje çalışmalarıyla uygulamaya
dönüştürmek
Güncel yazılım ve donanımları etkin bir biçimde kullanmak
7
Takım içinde ve bireysel çalışabilme becerisi kazanmak
5
8
9
10
1
2
3
Matematik ve fen bilimleri hakkında genel kavrama yeteneği edinmek
ve analitik düşünme alışkanlığı kazandırmak
Elektrik-Elektronik Mühendisliği ile ilgili temel konularda bilgi birikimi
oluşturmak
Mühendislik problemlerini saptama, tanımlama, formüle etme ve
çözme becerisi ile bu amaca uygun analiz ve modelleme yöntemlerini
seçme ve uygulama yeteneği kazandırmak.
4
X
X
X
Sözlü ve yazılı iletişim kurma becerisi kazanmak. Yabancı bir dili
meslekî yaşamda etkin biçimde kullanmak
Yaşam boyu öğrenmenin gerekliliği bilinci; bilgiye erişebilme, bilim ve
teknolojideki gelişmeleri izleme ve kendini sürekli yenileme becerisi
kazanmak
Mesleki sorumluluk ve etik bilinç kazanmak
AKTS/İŞ YÜKÜ TABLOSU
Ders İçi
Ders Dışı
Sınavlar
İş Yükü (Saat)
Ders Saati ( 14 x Haftalık Ders Saati)
56
Ödev
14
Araştırma
14
Ön Hazırlık, Pekiştirme Çalışmaları
14
Diğer Faaliyetler
14
Ara Sınav (Ara Sınav Sayısı x Ara Sınav Süresi)
1
Yarıyıl Sonu Sınavı
28
Toplam İş Yükü
141
Toplam İş Yükü / 25 (s)
5,64
AKTS Kredisi
5
6