ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ

ENERJİ SİSTEMLERİ
MÜHENDİSLİĞİ
ELEKTRİK ELEKTRONİK DEVRE
TASARIMI LABORATUVAR FÖYLERİ
LABORATUVAR KURALLARI
1. Laboratuvarlar programda belirtilen giriş ve çıkış saatlerine uygun olarak yapılır.
Deneylere 5 dakika ve daha fazla süre geç kalan öğrenciler deneye alınmaz.
2. Laboratuvara gelmeden önce öğrencilerin o gün yapacakları deneylere ait deney föyünü
dikkatle okumaları ve deneyle ilgili teorik bilgileri çeşitli kaynaklardan öğrenmiş olmaları
gerekir.
3. Deney föyünde istenilen “ön çalışma” deneye gelmeden önce öğrenci tarafından
tamamlanmalıdır. Ön çalışmayı yapmayan öğrenci deneye alınmaz. Deney föyü olmadan
gelen öğrenci deneye alınmaz.
4. Geçerli bir sebepten dolayı deneye katılamayan öğrenciler (durumlarını resmi olarak
belgelemek koşuluyla) yarıyıl sonunda belirlenecek olan telafi haftasında bu deneyi
yapacaklardır.
Birden
fazla deneye
katılmayan öğrenci
ancak
bir deneyi
telafi
edebileceklerinden diğer deneylere girmemiş ve sıfır almış kabul edileceklerdir.
5. Öğrencinin gelmediği deneyden alacağı not sıfırdır.
6. Raporlar, deneyin yapıldığı tarihten bir hafta sonra deney saatinde teslim edilmelidir.
Teslim edilmeyen raporların notu sıfır olarak belirlenecektir.
7. Teslim zamanından daha geç getirilen raporlar değerlendirilmeyecektir.
GENEL BİLGİLER VE UYARILAR
1. Deneyin sorunsuz ilerleyebilmesi için öğrencilerin, deneyi yaptıran Araştırma
Görevlilerinin tüm uyarı ve düzenlemelerine harfiyen uyması gerekmektedir.
2. Öğrenciler her masada iki kişi olacak şekilde gruplara ayrılacaktır. Grup arkadaşınızı seçme
özgürlüğüne sahipsiniz. Diğer grupları rahatsız etmemek ve daha verimli bir çalışma ortamı
sağlamak için laboratuvarda “ALÇAK SESLE” konuşmak zorunludur.
3. Cep telefonu, radyo, mp3 çalar gibi deney ölçümlerini etkileyebilecek veya başkalarını
rahatsız edebilecek elektronik aletleri laboratuvar içinde kapalı tutunuz.
4. Çanta, mont vs. gibi eşyalarınızı deney masasının üzerine koymayınız.
5. Deney sırasında genel ahlak ve temizlik kurallarına uyulmaya özen gösterilmelidir. Deney
masalarının veya ekipmanların üzerine hiçbir şekilde yazı yazmayınız.
6. Deney masasında yiyecek ve içecek bulundurulmamalıdır.
7. Deney sonunda deney masası toparlanmalı, ilgili elektrik bağlantıları kesilerek, tabureler ve
masa düzenli bir biçimde bırakılmalıdır.
8. Devreleri kurarken ve devre üzerinde değişiklik yapılırken (eleman ekleme/çıkarma,
bağlantı değiştirme) gerilim kaynağı mutlaka kapalı olmalıdır.
9. Devreye gerilim verilmeden önce yapılan bağlantıların doğruluğu kontrol edilmelidir.
10. Tüm devrelerin besleme ve toprak hatlarının doğru olarak bağlandığından ve besleme
gerilimi ile toprak hattı arasında kısa devre oluşmayacağından emin olunmalıdır.
1. GİRİŞ
Enerji Sistemleri Mühendisliği, Elektrik-Elektronik Mühendisliği ve Makine Mühendisliğinin
karma bir yapısından oluşan uygulamalı bir bilim dalıdır. Laboratuvar deneyleri, derslerde
verilen teorik bilgilerin fiziksel ortamda nasıl uygulanacağını sistemli bir şekilde ortaya
koyar. Bu yüzden Enerji Sistemleri Mühendisliği öğreniminde laboratuvar deneylerinin çok
önemli bir yeri vardır.
Şekil 1.1. Elektrik-Elektronik laboratuvarı cihazları
Elektrik-Elektronik laboratuvarında III. dönemde verilen EMB-207 Temel Elektrik ve IV.
dönemde verilen EMB-208 Temel Elektronik derslerinin uygulamaları yapılacaktır. ElektrikElektronik laboratuvarı deneyleri genel olarak iki kısımdan oluşmaktadır:
1. Ele alınan devrenin teorik olarak çözülerek istenen niceliklerin hesaplanması
2. Devrenin board üzerine kurularak hesaplanan niceliklerin ölçülmesi
Yukarıda verilen 1. madde öğrenciler tarafından "ön çalışma" kapsamı içerisinde deneye
gelmeden önce yapılıp hazırlanacaktır. Deneyleri bu şekilde gerçekleştiren öğrenciler, derste
öğrendikleri analiz metotlarını gerçek devreler üzerinde tekrar etmiş olacaklar. 2. Madde ise
deney sırasında uygulamalı olarak gerçekleştirilecektir.
2. ELEKTRİK-ELEKTRONİK LABORATUVARI VE CİHAZLARI TANIMA
A. Deneyin Amaci
Laboratuvar araçları hakkında genel bilgi edinmek. Elektrik devrelerindeki akım, gerilim,
direnç gibi fiziksel büyüklüklerin ölçülmesi ve bu büyüklüklerin ölçülmesinde kullanılan ölçü
aletlerini tanımak. Laboratuvarda uyulması gereken kuralları kavramak.
B. Kullanilacak Araç Ve Malzemeler
1. DC güç kaynağı
4. Sinyal Jeneratörü
2. El tipi multimetre
5. Protoboard
3. Osiloskop
C. Deney İle İlgili Ön Bilgi
Laboratuvarımız:
Elektronik Laboratuvarımız, 106 m² alana sahip olup 10 deney masasından oluşmakta ve 30
öğrencinin deney yapabilmesine imkan sağlamaktadır. Bu masalardan birinin genel görünümü
Şekil 2.1’de verildiği gibidir.
Şekil 2.1. Elektrik-Elektronik Laboratuvarındaki bir deney masasının genel görünümü
Şekil 2.1’den de görüleceği gibi, bir laboratuvar masasında çeşitli cihazlar bulunmaktadır.
Güç Kaynakları: DC Güç Kaynağı, Sinyal Jeneratörü (AC güç kaynağı). Bu cihazlar
laboratuvarda kurulan devrenin elektriksel olarak beslenmesinde kullanılırlar.
Ölçü Aletleri: El tipi multimetre, Osiloskop. Bu cihazlar, devrede bulunan herhangi bir
eleman üzerindeki akım, gerilim ve direnç ölçümlerini gerçekleştirmek için kullanılırlar.
Protoboard: Üzerine devre kurulması için kullanılan bir düzenektir.
*** Laboratuvar çalışmasında önce protoboard üzerine gerekli elemanlar yerleştirilerek devre
kurulur, sonra güç kaynağı bağlanarak devreye elektrik verilir. En sonunda da ölçü aletleri
kullanılarak gerekli ölçümler yapılır.
 DC Güç Kaynağı
DC Güç Kaynağı, protoboard üzerine kurulacak devrelere elektrik beslemesi sağlamak
amacıyla voltaj kaynağı olarak kullanacağımız cihazdır. Laboratuvarımızda GW-INSTEK,
GPS-3303 kodlu ürün yer almaktadır.
8
3
6
7
1
2
4
5
Şekil 2.2. DC Güç Kaynağı
Laboratuvarımızda bulunan ve Şekil 2.2’de görülen MCP marka DC güç kaynağı temel olarak
sekiz kısımdan oluşmaktadır:
1. I nolu ayarlı güç kaynağı,
2. II nolu ayarlı güç kaynağı,
3. Ayarlı kaynak seçim tuşları (bağımlı ya da bağımsız tuşu),
4. Sabit 5V’luk güç kaynağı ve kaynak çıkışı,
5. Ayarlı dc kaynak çıkışları (mavi negatif, kırmızı pozitif, GND toprak)
6. Çıkış sinyal anahtarı (çıkışı görebilmek için “on” durumda olmalı)
7. Açma Kapama tuşu
8. Dijital Ekran
Cihazımız iki ayarlı, bir sabit olmak üzere toplam üç tane kaynaktan oluşmaktadır. Her
kaynağın değişik renklerde (mavi, kırmızı ve sarı) olmak üzere değişik sayıda çıkışları
mevcuttur. Bu dönem yapılacak olan deneylerde pozitif olan kırmızı uç ve negatif olan mavi
uç kullanılacaktır.
Şekil 2.2’de görülen DC Güç kaynağının I ve II nolu ayarlı kaynakları aslında birbirinin
aynısı olup, her bir kaynak 0-30 V arası istenen değere ayarlanabilir voltaj üretirler. Her iki
kaynak, kırmızı uç ile mavi uç arasında ayarlanan değerde potansiyel fark oluşturur. Şimdi,
örneğin 8V’luk bir voltaj kaynağına ihtiyaç duyduğumuzu farz edelim. 8V’luk voltajı I veya
II nolu ayarlı kaynaktan her hangi birini kullanarak kolayca oluşturabiliriz. Bunun için
yapılması gereken adımlar şunlardır:
1. İlk başta Güç Kaynağının 3. kısmı olan ayarlı kaynak seçim tuşları kullanılarak kaynak
seçimi yapılmalıdır. Bu kısım iki tuştan ibaret olup, I ve II nolu ayarlı kaynakların değişik
bağlanma şekillerini ifade eder:
INDEP: Her iki tuş, basılı değil konumunda ise iki ayarlı kaynak birbirinden bağımsız çalışır. Yani elimizde iki
farklı kaynak vardır ve birbirinden bağımsız değerlere ayarlanabilir (örneğin 3V ve 15V gibi).
SERIES: Soldaki tuş basılı konumda, sağdaki tuş basılı değil konumunda ise kaynaklar cihazın içinden birbirine
seri bağlanır. Bu durumda ayarlamalar, 'master' olan 2. bölgedeki kaynaktan yapılabilir.
PARALLEL: Her iki tuş, basılı konumda ise iki kaynak birbirine paralel demektir. Bu durumda ayarlamalar,
'master' olan 2. bölgedeki kaynaktan yapılabilir.
2. Daha sonra seçili ayarlı kaynak tarafındaki “CURRENT” yazan akım ayar tuşu ile
“VOLTAGE” yazan voltaj ayar tuşları kullanılmalıdır. İlk durumda herhangi bir ayarlama
yapılmadan üzerinde “C.C” yazan lamba kırmızı olarak yanarken, “C.V.” yazan lamba sönük
durumdadır. Ekranda ise 0 V görülmelidir.
3. Kırmızı lamba yanıyorken voltaj ayar tuşu ile istenilen voltajı ayarlamak mümkün değildir.
Bu nedenle önce akım ayar tuşu sağa doğru az bir miktar çevrilerek, kırmızı lamba sönüp
“C.V.” lambası yeşil olarak yanıncaya kadar bir miktar akım verilmelidir. Yeşil lamba
yandıktan sonra voltaj ayar tuşu ekranda 8 V görülene kadar sağa doğru çevrilir.
4. Ayarlı kaynağın kırmızı çıkışına kırmızı kablo ve mavi çıkışına siyah kablo bağlanarak,
kabloların diğer uçları devrede ilgili yere bağlanarak, devre 8 V’luk gerilim ile beslenmiş
olur.
Cihazımız bir voltaj kaynağı olduğu için, istenen voltaj değeri ayarlanabilir, ancak üretilen
akımın üzerinde herhangi bir kontrol imkânı yoktur. Üretilen voltaj ve devredeki toplam
direnç miktarıyla orantılı bir değerde akım üretilir. Bu güç kaynağından çekilebilecek akım
miktarı maksimum 3 A’dir.
HATIRLATMA 1:
Eğer “C.C.” lambası yanıyorsa kaynak, istenen gerilimi üretemiyor anlamına gelir. Böyle bir durumda iki sorun
olabilir:
1. İlk başta yeterince akım verilmemiştir.
Çözüm: Akım ayar tuşu sağa doğru az bir miktar çevrilerek gerekli akım sağlanır.
2. Akım yeterince verilmiş ancak “C.C.” lambası hala yanıyorsa, muhtemelen devremizde bir kısa devre vardır
ve kaynaktan 3A’den fazla akım çekilme durumu vardır.
Çözüm: Güç kaynağı hemen kapatılır ve devredeki kısa devre problemi çözülür. Daha sonra tekrar güç kaynağı
açılır.
HATIRLATMA 2:
Ayarlı kaynak seçim tuşlarını ne zaman kullanırım?

Eğer tek bir kaynağa ihtiyacım varsa ve 30 V/3 A yeterliyse, INDEP konumu ile tek bir ayarlı kaynağını
kullanabilirim.

Eğer aynı anda iki farklı kaynağa ihtiyacım varsa, INDEP konumunda her iki ayarlı kaynağı bağımsız
olarak kullanabilirim.

Değeri 30 V'tan daha fazla bir voltaj kaynağına veya ± 15V gibi simetrik iki voltaj kaynağına ihtiyacım
varsa, SERIES konumu işimi görecektir. Bu durumda INDEP konumu yetersiz kalır.

3A'den daha fazla akım çekmek istiyorsam, PARALLEL konumunu kullanmalıyım.

Güç kaynağının 4. kısmı olan sabit voltaj kaynağı yalnızca 5V’luk voltaj üretir. Eğer 5V’luk bir
kaynağa ihtiyacınız varsa, ayarlı kaynakları kullanarak 5V’u ayarlamak yerine doğrudan bu kaynağı
kullanabilirsiniz. Böylece, ayarlı kaynaklarda uygulanan adımlar uygulanmadan doğrudan kablolar
kaynağın çıkışına bağlanarak 5V elde edilebilir olması bize kolaylık sağlayacaktır.
 Sinyal Jeneratörü
Sinyal jeneratörü, protoboard üzerine kurulacak devrelere istenilen frekansta ve genlikte
sinüs, üçgen, kare ve rampa dalga şekilleri üretmeye yarayan cihazdır. Zamanla değişen (AC)
gerilimleri ürettiğinden AC güç kaynağı olarak da düşünülebilir. Laboratuvarımızda GW
Instek firmasının Goodwill SFG-1003 kodlu ürünü kullanılmaktadır.
Şekil 2.3. Sinyal jeneratörü
Laboratuvarımızda bulunan ve Şekil 2.3’te görülen GW Instek marka Sinyal Jeneratörü’ne ait
temel kısımlar aşağıdaki gibidir:
1. Açma kapama tuşu
2. Dijital Ekran
3. Frekans ayarı (manual)
4. Dalga şekli seçim butonu (üçgen, kare, sinüs, rampa, TTL ve CMOS çıkış)
5. Offset ayarı (DC ekleme)
6. Çıkış sinyali genlik ayarı
7. Sinyal çıkışları
8. Frekans giriş butonu (3 Mhz’e kadar giriş yapılabilir)
9. Çıkış sinyal anahtarı (çıkış alabilmek için “on” konumunda olmalı)
Cihazımız “TTL Output” (sadece kare dalga çıkış veren ve dijital devrelerde kullandığımız)
ve “Output 50 Ω” (analog çıkış) olmak üzere iki çeşit sinyal üretebilmektedir. Laboratuvarda
farklı şekillerde, istenilen frekans ve genlikte analog çıkış alabildiğimiz “Output 50 Ω”
çıkışını daha fazla kullanacağız.
Şekil 2.4. Sinyal jeneratörü çıkış kablosu
Sinyal Jeneratörü’nün “TTL” ya da “Output 50 Ω” çıkışına solda Şekil 2.4’te görülen kablo
bağlanarak sinyal elde edilir ve protoboard üzerinde kurulan devreye verilir. Kablonun
kırmızı ucu pozitif, siyah ucu negatif olarak görülür.
Shift butonuna basılarak frekans girişi yapılabilir, sinyal jeneratörü üstünde shift basılı iken 8,
9 ve 0 rakamları kullanılarak sırasıyla Mhz, Khz ve Hz seçimleri aktif edilebilir. Daha sonra
yine rakamlar ve nokta kullanılarak istenilen frekans yazılabilir. 3 nolu manual frekans ayar
butonu ise bize ince ayar yapmamızı sağlamaktadır, örneğin 53 Hz’lik bir sinyali ayarlarken
bu butondan faydalanabiliriz.
Eğer sinüs bir sinyal alınacak ve bu sinyale DC bir gerilim eklenecekse bunu “offset”
butonunu kullanarak elde edebiliriz.
 El Tipi Multimetre
Multimetre (multi-çok, çoklu, metre-ölçüm), isminden de anlaşılacağı üzere elektriksel olarak
çok çeşitli ölçümler yapabilen cihazlardır. Bir multimetre ile akım, voltaj, direnç, kapasite, vb.
gibi çok çeşitli elektriksel niceliklerin ölçümleri mümkündür.
İki çeşit multimetre vardır:

El tipi multimetre

Masa tipi multimetre
El tipi multimetreler taşınabilir olduklarından kullanımı en çok tercih edilen multimetrelerdir.
Laboratuarımızda, Şekil 2.5’te görüldüğü gibi GW Instek firmasının GDM-357 ürün kodlu
dijital el tipi multimetreler mevcuttur.
2
1
3
4
Şekil 2.5. El tipi multimetre
Bu multimetrede işaretlenmiş kısımlar:
1. Açma/kapama tuşu
2. Ekran
3. Kademe tuşu
4. Çıkış uçları
Kademe tuşu multimetrenin en önemli işlevsel kısmıdır. Kademe tuşu dairesel bir şekilde
hareket ederek, istenilen niceliğin seçimini sağlar. Bu nicelikler içinde en çok kullanılanları;
V
: DC Voltaj
V
: AC Voltaj
mV
: Mili Volt
A
: Akım (Amper)
mA
: Akım (miliamper)
μA
: Akım (mikroamper)
Hz
: AC gerilim frekansı
Ω
: Direnç (ohm)
mV, mA gibi seçenekler hem AC hem de DC ölçümlerde kullanılabilmekte olup ölçü aletinin
ekranına bakarak, hangi modda olunduğu kolayca anlaşılabilir.
Multimetreyi ölçüm yapılacak devre elemanına bağlamak için ara eleman olarak “prob”
denilen kablolar çıkış uçlarına bağlanır. Bunun için cihazın dört tane çıkışı vardır. Ölçüm
yaparken, siyah prob her zaman, “COM” çıkışına bağlanmalı, kırmızı prob ise ne ölçülmek
isteniyorsa ona bağlanmalıdır: yani, amper düzeyinde akım ölçümü yapılacağı zaman amper
düzeyindeki ölçümler için “10A” çıkışına; miliamper düzeyinde akım ölçümü yapılacağı
zaman “mA” çıkışına bağlanmalıdır; direnç, gerilim veya kapasite ölçüleceği zaman ise “V”
çıkışına bağlanmalıdır.
HATIRLATMA 3: Multimetrelerde her ölçüm öncesi dikkat edilmesi gereken bir “üçlü kontrol kuralı” vardır:
Önce kademe tuşu ile uygun nicelik seçilir. Sonra, doğru niceliğin seçilip seçilmediği ekrandan kontrol edilir.
Sonunda, probların doğru çıkışa bağlanıp bağlanmadığına bakılır. Burada özellikle probların doğru çıkışa
bağlanıp bağlanmadığı çok önemlidir. Örneğin, akım kademesi seçilip problar yanlışlıkla voltaj çıkışlarına
bağlanırsa, bu durumda multimetrenin sigortası atabilir. Özellikle ardı ardına yapılan sürekli ve karışık nicelik
ölçümlerinde, probların yerinin düzeltilmesi sıkça unutulmaktadır. Bu nedenle her ölçüm öncesi üçlü kontrol
kuralını uygulamak olmazsa olmaz önceliğimizdir.
 Osiloskop
Osiloskop; DC ve AC her türlü sinyalin genliğini ve frekansını ölçebildiğimiz aynı zamanda
dalga formunu da görüntüleyebildiğimiz ölçüm cihazıdır. Laboratuvarımızda Şekil 2.6’da
görüldüğü üzere GW-Instek firmasının üretmiş olduğu Goodwill GDS 1052-U kodlu ürünü
kullanmaktayız.
Şekil 2.6. Osiloskop
Osiloskop zamana bağlı olarak gerilimi (V/t) okumaya yarayan ve kullanımı basit bir cihazdır.
Burada zaman (t) X-ekseninde yer almakta olup, gerilim(V) Y-ekseninde yer almaktadır.
Osiloskop ekranını incelediğimizde yatayda 10, düşeyde 8 eşit kareden oluştuğunu ve
genellikle bu karelerin her birinin 1 cm uzunluğunda olduğunu görebiliriz.
Osiloskopta 2 farklı kanal bulunmakta olup, aynı anda ikisini de görebilme şansımız vardır.
Böylece bir devrenin giriş ve çıkışını aynı anda gözlemleyebilmekteyiz. Sinyal çıkışlarını
“CH1” ve “CH2” yazan yerlere problarımızı bağlayarak elde edebiliriz. Osiloskopu kalibre
etmek için ise “EXT TRIG” çıkışını kullanırız. Probumuzu “EXT TRIG” çıkışına takıp
kırmızı ucu da şekil 7’deki gibi tepeden tepeye 2V kare dalga görebileceğimiz kalibrasyon
çıkışına bağlarsak şekil 7’deki gibi sinyal elde ederiz.
Şekil 2.7’de volts/div 0.5 V olarak ayarlanmıştır. Eğer volts/div ayarını değiştirerek ekranda
gördüğümüz şekil değişir fakat sonuç etkilenmez. Örneğin, volts/div 0.5 V iken Y
eksenindeki boy 4 kare olduğundan gerilim 2 V’tu. Eğer volts/div 1 V olarak ayarlanırsa Y
eksenindeki sinyali toplam 2 karede görebileceğiz. Volts/div sekmesindeki değer Y
eksenindeki her kareye düşen miktarı göstermektedir.
Şekil 2.7. Osiloskop EXT TRIG çıkışı ile kalibrasyon
Time/div
ayarı,
X
ekseninde
görüntülediğimiz
zamanı
ve
dolayısıyla
frekansı
etkilemektedir.Burada ekrandaki şekli X-Pos ve Y-Pos butonlarını kullanarak sağa sola veya
aşağı yukarı hareket ettirme imkânımız vardır. Böylece görüntümüz simetrik olur ve
osiloskopu tam anlamıyla kalibre etmiş oluruz. Osiloskopu kalibre ettikten sonra devre
analizlerinde rahatlıkla kullanabiliriz. Devreye bağlar bağlamaz “Autoset” tuşuna basarsak
bize sinyali otomatik olarak ekranda verir, daha sonra bu sinyali daha net görmek istiyorsak
volts/div ve time/div ayarlarını kullanarak optimizasyon yaparız. Eğer sinyalin frekansı çok
yüksekse ve sinyal görmemizi zorlaştıracak şekilde hızlı olarak ekranda hareket ediyorsa
“Run/Stop” butonu ile sinyali durdurup analiz edebiliriz.
Osiloskopta ayarlamak istediğimiz sinyal hangi kanala bağlı ise ayarları o kanalda
yapmalıyız.Sarı renkli CH1 ve mavi renkli CH2 ile kanal seçimlerini aktif ya da deaktif
edebiliriz.
Osiloskopta ekranda “AC Coupling” seçersek sinyalin sadece AC bileşenini görüntüler ve DC
bileşenleri elemiş oluruz, “DC Coupling” seçersek sinyalin gerçek halini yani hem AC hem
de DC bileşenlerini görüntüleriz; “GND” seçeneğinde ise sinyalden bağımsız olarak toprağı
görüntüleyebiliriz – bu seçenek osiloskopun kalibre olup olmadığını da bize gösterir burada
işaretçimiz sıfır çizgisinde olmalıdır.
Osiloskopta “X-Y modu” seçmeniz durumunda CH1 ve CH2 kanallarına bağladığınız
sinyallerin birbirlerine göre davranış karakteristiğini çıkarabilir ve inceleyebilirsiniz –
özellikte çıkış/giriş karakteristiğini merak ettiğimizde başvurabileceğimiz bir seçenektir.
Osiloskop ekranının hemen sağında fonksiyon tuşları mevcut olup burada sinyalin tersini
alabilir, yükseliş zamanı, max./min. değerlerini, frekansını ve rms değerini hesaplatabilirsiniz.
 Protoboard
Protoboard, laboratuvar ortamında kolay devre kurmak amacıyla kullanılan bir elemandır.
Şekil 2.8’de görülen protoboard üzerinde, dirençlerin bacaklarının yerleştirilmesi için
oluşturulmuş çok sayıda nokta şeklinde yuva mevcuttur. Protoboard üzerindeki her bir yuvaya
yalnızca bir direnç bacağı bağlanır. Bu yuvalar birbirlerinden tamamen bağımsız olmayıp,
kendi aralarında gruplar halinde -protoboardın iç kısmında- kısa devre edilmişlerdir.
Yuvaların birbirinden bağımsız olmayıp bu şekilde bağlantı kurulmasının en önemli avantajı,
iki veya daha fazla direncin uçlarını birbirine bağlamada sağladığı kolaylıktır.
Şekil 2.8. Protoboard
Protoboard’ı Nasıl Kullanmalıyım?
Protoboard kullanılırken dikkat edilmesi gereken en önemli nokta, direncin uçlarını aynı
bağlantı üzerine getirmemektir. Eğer getirilirse, direnç kısa devre edilmiş ve sanki
protoboarda hiç bağlanmamış gibi olur. O halde direncin uçlarını farklı bağlantılar üzerine
yerleştirmek en doğru kullanım şekli olacaktır. Şekil 2.9’da protoboard kullanım şekilleri
verilmiştir.
Şekil 2.9. Protoboard üzerindeki direnç bağlantıları
HATIRLATMA 4: Herhangi bir devre elemanının uçları düz bir telin uçlarına bağlanırsa, eleman kısa devre olur
ve hiçbir elektriksel özellik sergilemez.
HATIRLATMA 5: Protoboard üzerinde devre kurarken, elemanları kağıt üzerindeki devre düzenine göre
yerleştirmek çok önemlidir. Bu, bize ileride devreye tekrar baktığımızda veya bir başkası devremize baktığında
elemanların yerini bulmakta kolaylık sağlayacaktır. Özellikle karmaşık devrelerde bu yerleşim düzeninin önemi
çok büyüktür. Eğer bu düzen verilmezse devredeki arızaların tespitinde zorluklar yaşanması büyük olasılıktır.
Örnek: Aşağıdaki devreyi protoboard üzerine kurunuz.
Şekil 2.10. Protoboard üzerinde devre düzeneğinin kurulması
Protoboard üzerine devre kurulurken yukarıdaki açıklamalara uygun olarak, dirençler şemada
verilen aynı düzende protoboard üzerine yerleştirilir (yani yatay direnç yatay bir şekilde ve
dikey direnç dikey bir şekilde). Yerleştirme işlemi sırasında da dirençlerin kısa devre
edilmemesine özen gösterilir.
 En Temel Elektronik Devre Elemani: Direnç (Resistor)
Direnç, elektronikte en sık kullanılan devre elemanıdır. Direncin en önemli özelliği –adından
da anlaşılacağı üzere- üzerinden akan akıma karşı koyması ve üzerinde bir miktar güç
harcamasıdır. Şekil 10’da değişik özelliklerde üretilmiş dört tane direnç görülmektedir.
“Düşük wattlı direnç” olarak adlandırılan şekildeki ilk üç direnç, en çok kullanılan direnç
çeşitlerindendir. Direncin boyutu ile üzerinde harcadığı güç miktarı birbiri ile doğru
orantılıdır. Düşük wattlı dirençler genellikle çeyrek wattlık (0.25W), yarım wattlık (0.5W) ve
bir wattlık (1W) direnç şeklinde sınıflandırılırlar. Şekil 2.11’deki üç dirençten ortadaki çeyrek
wattlık, soldaki yarım wattlık ve sağdaki ise bir wattlık dirençlerdir. Bu değerler, bir direncin
üzerinde harcanabilecek maksimum güç değerini gösterir. Bu değerin üstünde güç
harcanmaya kalkışılırsa, direnç elemanı kor halini alıp yanar ve kullanılamaz hale gelir.
Şekilde en sağdaki dördüncü direnç ise boyutundan da anlaşılacağı üzere “yüksek wattlı
direnç” veya kısaca “wattlı direnç” olarak adlandırılır. Düşük wattlı dirençlerin watt değeri
boyutlarından anlaşılırken, wattlı dirençlerin watt değeri doğrudan üzerinde yazar.
Şekil 2.11. Çeşitli direnç elemanları
Bir direncin watt değeri, aslında onun direnç değerini ifade etmez. Bir direncin esas değeri,
yani akıma karşı koyma kabiliyeti ohm (Ω) ile ifade edilir. Bir direncin değerini öğrenmek
için iki yol vardır:
a) Direnci Ω kademesinde multimetre ile ölçerek
b) Üzerinde bulunan renk kodlarından faydalanarak
a) Multimetre ile Direnç Ölçümü:
Multimetrenin yukarıda anlatılan genel kullanım özelliklerini hatırlayarak, bir direnci
multimetre ile nasıl ölçeceğimize bakalım: Bunun için önce multimetreyi ohmmetre olarak
ayarlamamız lazımdır. Bunun için önce multimetrenin ortasında bulunan kademe tuşunu “Ω”
kademesine ayarlarız (bu durumda ekranın kenarında Ω işareti görülmelidir), daha sonra
elimizdeki iki probdan siyah olanını COM çıkışına, kırmızı olanı ise “V” çıkışına bağlarız.
Artık multimetre, direnç ölçümü için hazır hale gelmiştir (Bknz. Şekil 2.12).
Şekil 2.12. Direnç ölçümü için hazır hale getirilmiş bir multimetre
Şimdi direncin değerini ölçebiliriz. Bunun için kırmızı probun boştaki diğer ucu direncin
herhangi bir bacağına, siyah probun boştaki diğer ucu ise direncin diğer bacağına bağlanır.
Böylece multimetre, direnç ölçümü için elemana paralel bağlanmış olur (Bknz. Şekil 2.13).
Şekil 2.13. Ohmmetrenin Dirence Paralel Olarak Bağlanması
Ekranda okunulan değer, direncin Ω cinsinden değeridir (Şekil 2.14). Bazı dirençlerin değeri
çok büyük olabilir. Bu durumda ekranın kenarında “kilo (k)”, “mega (M)” gibi harfler
görünecektir.
Şekil 2.14. Multimetre ile direnç ölçümü
b) Renk Kodları ile Direnç Değerinin Belirlenmesi:
Bir direncin değerini belirlemenin en kolay yolu, üzerinde bulunan ve “renk bandı” olarak
adlandırılan renkli şeritleri göz önüne almaktır (Şekil 14).
Tablo 2.1. Direnç renk kodları
Tablo 2.2. Direnç renk kodlama örnekleri
3. BASİT BİR ELEKTRİK DEVRESİ KURMA (OHM KANUNU)
3.1. Deneyin Amacı
Bu deneyde, Ohm kanunu işlenecektir. Seri ve paralel devrelere ohm kanunu uygulanıp,
teorik sonuçlarla deney sonuçlarını karşılaştıracağız ve doğrulamasını yapacağız.
3.2. Teorik Bilgi
Ohm Kanunu, gerilim, akım ve direnç arasındaki matematiksel ilişkiyi belirler. Bu bağıntıya
göre kapalı bir devrede akım gerilimle doğru orantılı, dirençle ters orantılıdır. Tek dirençten
oluşan bir devrenin şeması Şekil 3.1’de gösterilmiştir.
OHM
KANUNU
I
U
R
Şekil 3.1. Devre Şeması
3.2.1 Seri Devreler
Seri devrelerde akım eşdeğer direnç ile ters orantılıdır. Üç dirençli bir seri devrenin şeması
şekilde gösterilmiştir. Seri devrelerde eşdeğer direnç aşağıdaki gibi hesaplanır.
Reşd  R1  R2  R3
I1
I
V
V1
I2
V2
V3
Şekil 3.2. Seri Direnç Devresi
Seri devrelerde her direnç üzerinden aynı akım geçer. Devreye uygulanan toplam gerilim ise
her bir direncin üzerindeki gerilimin toplamına eşittir. Bu yüzden seri devrelere “gerilim
bölücü devre” de denir.
Akım;
I
U
Reşd
olur ve her direncin üzerinden geçen akım birbirine eşittir.
I  I R1  I R2  I R3
Toplam gerilim ise her bir direncin üzerindeki gerilimin toplamına eşittir.
U  U R1  U R2  U R3
Her bir direncin üzerindeki gerilim ise,
U R2  I R2  R2 ,
U R1  I R1  R1 ,
U R3  I R3  R3
olarak hesaplanır.
3.2.2 Paralel Devreler
Paralel devrelerde ana koldan geçen akım eşdeğer dirençle ters orantılıdır ve ana koldan geçen
akım her direncin üzerinden geçen akımların toplamına eşittir. Dirençler üzerindeki gerilim
ise birbirine eşittir. Bu yüzden paralel devrelere “akım bölücü devre” de denir. Üç dirençli
paralel bir devrenin şeması şekil 2.3’de gösterilmiştir. Paralel dirençlerin eşdeğer direnci;
1
1
1
1
 

Reşd R1 R2 R3
bağıntısıyla bulunur.
I
I1
V
R1
I2
Şekil 2.3 Paralel Devre
Bu devreden geçen ana akım;
R2
I3
R3
I
U
Reşd
olarak bulunur.
Her bir koldaki akım ise,
I R1 
U R1
R1
I R2 
U R2
R2
I R3 
U R3
R3
Olarak bulunur. Ayrıca ana koldaki akım,
I  I R1  I R2  I R3
olur.
Dirençlerin üzerindeki gerilimler ise birbirine eşittir.
U  U R1  U R2  U R3
3.3. Ön Çalışma
3.3.1. Şekil 3.1’deki devrede R direnci üzerindeki akımı hesaplayınız. Tablo 1’deki ilgili
yerleri doldurunuz. (Gerilim değeri sırasıyla 0, 2, 4, 6, 8 12 volt iken direnç değeri 100 Ω, 150
Ω, 330 Ω için hesaplayınız.)
3.3.2. Şekil 3.2’deki devrede ana akımı ve her direncin üzerindeki akım ve gerilim değerlerini
hesaplayınız(U = 12, 8, 4 V) (R1= 5 kΩ R2= 2.2 kΩ R3=3.3 kΩ). Tablo 2’yi doldurunuz.
3.3.3. Şekil 3.3’te sırasıyla 12 V, 8 V ve 4 V için ana akımı ve her direncin üzerindeki
gerilimi ve üzerinden geçen akımı hesaplayınız ve Tablo 3’ü doldurunuz.( R1= 5 kΩ R2= 2.2
kΩ R3=3.3 kΩ).
3.4. İşlem Basamakları
3.4.1. Deneyde Kullanılacak Malzemeler
Direnç : 100 Ω, 150 Ω, 330 Ω, 5 kΩ, 2.2 kΩ, 3.3 kΩ
Standart Laboratuvar Ekipmanları:
Osiloskop, DC Güç Kaynağı, Sinyal Jeneratörü, Dijital Multimetre, Protoboard
3.4.2. Şekil 3.1’deki devreyi kurunuz. Sırasıyla 100, 150 ve 330 Ω’luk dirençleri yerleştiriniz
akım değerlerini ölçünüz ve tabloya yerleştiriniz. Akım-gerilim karakteristiğini çiziniz.
3.4.2. Şekil 3.2’deki devreyi kurunuz. Devreye sırasıyla 12 V, 8 V ve 4 V uygulayınız. Her
direncin üzerindeki gerilimi ve üzerinden geçen akımı ölçünüz. R1= 5 kΩ R2= 2.2 kΩ R3=3.3
kΩ
3.4.3. Şekil 3.3’deki devreyi kurunuz. Devreye sırasıyla 12 V, 8 V ve 4 V uygulayınız. Her
direncin üzerindeki gerilimi ve üzerinden geçen akımı ölçünüz. R1= 5 kΩ R2= 2.2 kΩ R3=3.3
kΩ
3.5. SONUÇ
3.5.1. Ampermetre ve voltmetre devreleri için ön çalışmada bulmuş olduğunuz ve deneyde
elde ettiğiniz direnç değerleri için % cinsinden hata hesaplarını yapınız.
3.5.2. Hesaplanan ve ölçülen değerlerin aynı çıkmama nedenlerini yazınız.
3.5.3. Ohmmetre devresindeki skala lineer midir, sebebini basitçe açıklayınız.
4. THEVENİN ve NORTON DENEYLERİ
A. Thevenin Deneyi
A.1. Deneyin Amacı
Deneyin amacı, Thevenin Teoreminin öğrenilmesi ve laboratuvar ortamında test edilerek
sonuçlarının analiz edilmesidir.
A.2. Teorik Bilgi
A.2.1. Kaynak Dönüşümleri
Thevenin ve Norton teoremlerini kullanarak devre analizi yapmak için öncelikle kaynak
dönüşümlerinin nasıl yapıldığının bilinmesi gerekmektedir. Kaynak bağımlı veya bağımsız
oluşuna göre dönüşüm şu şekilde yapılır:
Şekil 4.1. Bağımsız Kaynak dönüşümü
Şekil 4.2. Bağımlı Kaynak Dönüşümü
A.2.2. Thevenin Teoremi ( Leon Thevenin 1857-1926 )
Çok sayıda elemanı bulunan herhangi bir devrenin bir elemanın veya sadece bir kısmının
incelenmesi gerektiğinde, tüm devreyi göz önüne almak yerine, incelenecek eleman yada
devre parçasını bütün olan devreden ayırıp geriye kalan devre parçasını bir kaynak ve buna
seri bağlı bir empedans ile temsil etmek suretiyle, inceleme basite indirgenebilir. Bu işlemde
kullanılan teoreme Thevenin teoremi denir ve elde edilen eşdeğer devreye Thevenin eşdeğer
devresi adı verilir.
Şekil 4.3. Temel bir elektrik devresi
Eşdeğer devre oluşturulurken ilgili eleman veya devre parçası ( şekilde R L ) devreden
çıkarılır, geriye kalan kısmın açık devre gerilimi Thevenin Eşdeğer Gerilimi olarak
adlandırılır.
Şekil 4.4. Thevenin Eşdeğer Geriliminin Hesaplanması
𝑉𝑎𝑏 = 𝑉𝑡ℎ
Daha sonra devredeki bütün kaynaklar söndürülerek Thevenin eşdeğer direnci bulunur.
Kaynaklar söndürülürken gerilim kaynaklarının kısa devre, akım kaynaklarının açık devre
yapılmasına dikkat edilmedir.
Şekil 4.5. Thevenin Eşdeğer Direncinin Hesaplanması
𝑅𝑒ş = 𝑅𝑡ℎ
Bir gerilim kaynağı ve ona seri bağlı bir empedanstan oluşan aşağıdaki Şekil 4.6’da görünen
eşdeğer devre, Şekil 4.3’teki devrenin Thevenin eşdeğer devresi olarak adlandırılır.
Şekil 4.6. Thevenin Eşdeğer Devresi
A.3. Ön Çalışma
A.3.1. Aşağıdaki devreler için;
RL direncinin uçları arasına bakıldığında Vth , Rth değerlerini bularak Thevenin eşdeğer
devresini çiziniz. RL üzerindeki gerilim ve akım değerlerini hesaplayarak aşağıdaki tablolarda
yerine yazınız.
RL =8.65 Ω
Şekil 4.7
𝐑 𝐋 = 𝟏 𝐊Ω
Şekil 4.8
A.4. İşlem Basamakları
A.4.1. Deneyde Kullanılacak Malzemeler
Direnç
: 1 kΩ, 2.2 kΩ, 3.3 kΩ, 4.7 kΩ, 5,6 kΩ
Standart Laboratuvar Ekipmanları: DC Güç Kaynağı, Dijital Multimetre, Protoboard
A.4.2. Laboratuvar ekipmanlarını kullanarak Şekil 4.7’deki devreyi kurunuz ve dijital
multimetre ile RL üzerindeki akım ve gerilim değerlerini ölçünüz. Sonuçları aşağıdaki tablo
4.1’e kaydediniz.
A.4.3. Laboratuvar ekipmanlarını kullanarak Şekil 3.8’deki devreyi kurunuz ve dijital
multimetre ile RL üzerindeki akım ve gerilim değerlerini ölçünüz. Sonuçları aşağıdaki tablo
4.2'ye kaydediniz.
Tablo 4.1. Şekil 4.7 deki Devre için değerler
Thevenin
Teoremi ile
bulunan değer
Deneyde
Ölçülen
Vth
Rh
X
X
iL
VL
Tablo 4.2. Şekil 4.8 deki Devre için değerler
Thevenin
Teoremi ile
bulunan değer
Deneyde
Ölçülen
Vth
Rh
X
X
iL
VL
A.5. SONUÇ
A.5.1. Ön hazırlık sorularında bulduğunuz akım ve gerilim değerleriyle, deneyde ölçtüğünüz
değerleri karşılaştırınız. Eğer fark var ise sebebini belirtiniz ?
A.5.2. Deneyde ölçtüğünüz değerler ile Thevenin Teoreminin doğrulandığını gösteriniz.
A.5.3. Bu deneyden neler öğrendiniz?
B. Norton Deneyi
B.1. Deneyin Amaci
Deneyin amacı, Norton Teoreminin öğrenilmesi ve laboratuvar ortamında test edilerek
sonuçlarının analiz edilmesidir.
B.2. Teorik Bilgi
B.2.1. Kaynak Dönüşümleri
Thevenin ve Norton teoremlerini kullanarak devre analizi yapmak için öncelikle kaynak
dönüşümlerinin nasıl yapıldığının bilinmesi gerekmektedir. Kaynak bağımlı veya bağımsız
oluşuna göre dönüşüm şu şekilde yapılır:
Şekil 4.9. Bağımsız Kaynak dönüşümü
Şekil 4.10. Bağımlı Kaynak Dönüşümü
B.2.2. Norton Teoremi ( Edward Lawry Norton 1898-1983)
Devre çözümünde kolaylık sağlayan bu teoremle iki nokta arasındaki karışık devre, çok basit
olan eş değer akım devresine dönüştürülür. Çok sayıda devre elemanı barındıran bir devrenin
bir elemanının ya da bir kısmının incelenmesinde, devrenin tamının incelenmesi yerine o
elemanı devreden çıkarıp, devrenin geri kalanını bir kaynak ve bir empedans ile
gösterebileceğimizi ve bu şekilde devre analiz yöntemine Thevenin Yöntemi denildiğini bir
önceki deneyde öğrenmiştik. Eğer eşdeğer devremiz bir akıma kaynağından ve ona paralel
bağlı bir empedanstan oluşursa buna da Norton eşdeğer devresi ve bu yönteme de Norton
yöntemi denir.
Daha basit bir ifade ile; Thevenin eşdeğer devresine "kaynak dönüşümü" uygularsak elde
edeceğimiz devre Norton Eşdeğer Devresi olacaktır. Bu nedenle Norton yöntemi ile devre
analizi yaparken, Thevenin yöntemi ile devre analizinde izlediğimiz adımları izlememiz
gerekmektedir.
Şekil 4.11. Elektrik Devresi
Eşdeğer devre oluşturulurken ilgili eleman veya devre parçası ( şekilde R L ) devreden
çıkarılır, geriye kalan kısmın kısa devre akımı Norton Eşdeğer akımı olarak adlandırılır.
Şekil 4.12. Norton Eşdeğer Akımının Hesaplanması
Daha sonra devredeki bütün kaynaklar söndürülerek Norton eşdeğer direnci bulunur.
Kaynaklar söndürülürken gerilim kaynaklarının kısa devre, akım kaynaklarının açık devre
yapılmasına dikkat edilmedir.
Şekil 4.13. Norton Eşdeğer Direncinin Hesaplanması
𝑅𝑒ş = 𝑅𝑁
Bir akım kaynağı ve ona paralel bağlı bir empedanstan oluşan aşağıdaki Şekil 4.14’te görünen
eşdeğer devre, Şekil 4.11’deki devrenin Norton eşdeğer devresi olarak adlandırılır.
Şekil 4.14. Norton Eşdeğer Devresi
B.3. Ön Çalışma
B.3.1. Aşağıdaki devreler için;
RL direncinin uçları arasındaki bakıldığında IN , RN değerlerini bularak Norton eşdeğer
devresini çiziniz. RL üzerindeki gerilim ve akım değerlerini hesaplayarak aşağıdaki tablolarda
yerine yazınız.
Aynı devreleri P-Spice kullanarak kurunuz ve RL üzerindeki gerilim ve akım değerlerini
ölçerek aşağıdaki tablolarda yerine yazınız.
𝑹𝑳 = 𝟐 Ω
Şekil 4.15
Şekil 4.16
𝑹𝑳 = 𝟏𝟎 Ω
Şekil 4.17
B.4. İşlem Basamakları
B.4.1. Deneyde Kullanılacak Malzemeler
Direnç
: 10 Ω, 100 Ω, 220 Ω, 330 Ω, 470 Ω
Standart Laboratuvar Ekipmanları:
DC Güç Kaynağı, Dijital Multimetre, Protoboard
B.4.2. Laboratuvar ekipmanlarını kullanarak Şekil 4.7'deki devreyi kurunuz ve dijital
multimetre ile RL üzerindeki akım ve gerilim değerlerini ölçünüz. Sonuçları aşağıdaki tablo
6.1'e kaydediniz.
B.4.3. Laboratuvar ekipmanlarını kullanarak Şekil 4.8'deki devreyi kurunuz ve dijital
multimetre ile RL üzerindeki akım ve gerilim değerlerini ölçünüz. Sonuçları aşağıdaki tablo
4.2'ye kaydediniz.
B.4.4. Laboratuvar ekipmanlarını kullanarak Şekil 4.9'daki devreyi kurunuz ve dijital
multimetre ile RL üzerindeki akım ve gerilim değerlerini ölçünüz. Sonuçları aşağıdaki tablo
4.3'e kaydediniz.
Tablo 4.1. Şekil 4.7 deki devre için değerler
IN
RN
X
X
iL
VL
iL
VL
iL
VL
Norton
Teoremi ile
bulunan değer
DENEY
Tablo 4.2. Şekil 4.8 deki devre için değerler
IN
RN
X
X
Norton
Teoremi ile
bulunan değer
DENEY
Tablo 4.3. Şekil 4.9 deki devre için değerler
IN
RN
X
X
Norton
Teoremi ile
bulunan değer
DENEY
B.5. Sonuç
B.5.1. Ön hazırlık sorularında bulduğunuz akım ve gerilim değerleriyle, deneyde ölçtüğünüz
değerleri karşılaştırınız. Eğer fark var ise sebebini belirtiniz ?
B.5.2. Deneyde ölçtüğünüz değerler ile Norton Teoreminin doğrulandığını gösteriniz.
B.5.3. Bu deneyden neler öğrendiniz?
5. DC DEVRELERİN ANALİZİ, KİRCHOFF’un GERİLİM ve AKIM YASASI
5.1. Deneyin Amaci
Deneyin amacı, DC devrelerde farklı elemanların nasıl davrandığını laboratuvar ortamında
incelemek ve DC devrelerde çevre ve düğüm yöntemlerini kullanarak Kirchoff’un akımlar ve
gerilimler yasasını incelemektir.
5.2. Teorik Bilgi
5.2.1. Çevre Akımlar Metodu
Elektrik devrelerinin çözümünde kullanılan en basit ve en kolay yöntemlerden biri çevre
akımları yöntemidir. Bu yöntemde devrenin her bir gözü için bir çevre akımı seçilir.
Gözlerden seçilen çevre akımlarına göre Kirchoff’un gerilimler denklemi, her bir göz için
yazılır. Göz adedi kadar bilinmeyen çevre akımı ve denklemi bulunur. Denklem çözülerek her
bir gözün çevre akımı hesaplanır. Çevre akımlarından da kol akımları kolaylıkla bulunabilir.
Şekil 5.1. Kirchoff’un gerilimler ve akımlar yasası için kullanılacak eşdeğer devre
Çevre 1:
−𝑉𝑠 + 𝑉1 + 𝑉2 + 𝑉5 = 0
(1)
Çevre 2:
−𝑉2 + 𝑉3 + 𝑉4 = 0
(2)
5.2.2 Düğüm Gerilimleri Metodu
Düğüm gerilimleri metodu temelde, temel düğümlere bir gerilim atanarak ve her düğüm için
Kirchoff’un akım kanunun yazılmasını temel alan bir yöntemdir. Bu yöntemle bütün temel
düğümlerdeki gerilimler hesaplanır. Bu değerler devrenin diğer noktaları için bir referans
özelliği taşır. Bu değerler vasıtasıyla devrenin herhangi bir noktasından geçen akımı veya
herhangi iki nokta arasındaki gerilimi hesap etmek mümkündür.
Şekil 4.1’ deki devreye düğüm gerilimleri yasasını uygularsak;
Düğüm a:
−𝐼𝑠 + 𝐼1 = 0
(3)
Düğüm b:
−𝐼1 + 𝐼2 + 𝐼3 = 0
(4)
Düğüm c:
−𝐼3 + 𝐼4 = 0
(5)
Düğüm d:
−𝐼2 − 𝐼4 + 𝐼5 = 0
(6)
5.3 Ön Çalışma
5.3.1. Şekil 5.2.’de gösterilen devre için,

A ve B düğümlerinin gerilimlerini hesaplayınız.

Devredeki dal akımları I1, I2, I3, I4, I5’i, bağımsız gerilim kaynaklarının değerlerini ve
önceki adımda bulduğunuz düğüm gerilimlerini kullanarak hesaplayınız.

Bağımsız gerilim kaynaklarının gücünü bulunuz ve ne kadar güç sağladıklarını veya
harcadıklarını hesaplayınız.
Şekil 5.2. Ön Çalışma Devresi 1
5.3.1. Şekil 5.3.’de gösterilen devre için,
 Çevre Akımları IA, IB, IC’yi hesaplayınız.
 Devredeki dal akımları I1, I2, I3, I4, I5’i, bağımsız gerilim kaynaklarının
değerlerini ve önceki adımda bulduğunuz çevre akımlarını kullanarak
hesaplayınız.
 Bağımsız gerilim kaynaklarının gücünü bulunuz ve ne kadar güç sağladıklarını
veya harcadıklarını hesaplayınız.
Şekil 5.3. Ön Çalışma Devresi 2
5.4 İşlem Basamakları
5.4.1. Deneyde Kullanılacak Malzemeler
Direnç
: 2.7kΩ, 5.6 kΩ, 12 kΩ, 22 kΩ
Standart Laboratuvar Ekipmanları: Osiloskop, DC Güç Kaynağı, Sinyal
Jeneratörü, Dijital Multimetre, Protoboard
5.4.2. Şekil 5.2’de verilen devreyi kurunuz ve devre elemanlarının değerlerini ön çalışmada
verilen değerlere ayarlayınız. A ve B düğümlerinin gerilimlerini ve I1, I2, I3, I4, I5 akımlarını
ölçünüz. Tablo 5.1’i tamamlayınız.
Tablo 5.1. Düğüm Gerilimi Devre Parametreleri
Veri
Ö𝐧 Ç𝐚𝐥ış𝐦𝐚
𝐃𝐞𝐧𝐞𝐲
VA
VB
I1
I2
I3
I4
I5
5.4.3. Şekil 5.3’de verilen devreyi kurunuz ve devre elemanlarının değerlerini ön çalışmada
verilen değerlere ayarlayınız. I1, I2, I3, I4, I5 dal akımlarını ve IA, IB, IC çevre akımlarını
ölçünüz. Tablo 5.2’yi tamamlayınız.
Tablo 5.2. Çevre Akımı Devre Parametreleri
Veri
Ö𝐧 Ç𝐚𝐥ış𝐦𝐚
𝐃𝐞𝐧𝐞𝐲
IA
IB
IC
I1
I2
I3
I4
I5
5.5.
SONUÇ
5.5.1. Teorik ve deneysel sonuçları karşılaştırınız. Eğer farklılık varsa nedenlerini
açıklayınız.
5.5.2. Bu deneyden neler öğrendiniz?
6. RL,RC ve RLC DEVRELERİNDE DC GEÇİCİ DURUM ANALİZİ
6.1.
Deneyin Amaci
Deneyin amacı, indüktans, kapasitans terimlerinin öğrenilmesi, zaman sabitinin ne olduğunun
kavranması, 1. ve 2. dereceden elektrik devrelerinin davranışlarının incelenmesidir.
6.2.
Teorik Bilgi
6.2.1. Ön Bilgi
Bir devrenin zamana bağlı analizini yapmak için devreye ait denklemler elde edilmeli ve bu
denklemler çözümlenmelidir. Bağımsız kaynaklar, dirençler, kapasitanslar ve indüktanslar
içeren bir devrenin analizini yaparken elde edilen denklemler, empedansı direnç ve
kapasitanstan oluşan RC (resistor- capacitor) devrelerde ve empedansı direnç ve indüktanstan
oluşan RL (resistor-inductor) devrelerde 1. dereceden, empedansı direnç, kapasitans ve
indüktanstan oluşan RLC (resistor-capacitor-inductor) devrelerinde ise 2. dereceden
diferansiyel denklem olarak karşımıza çıkmaktadır.
Elde edeceğimiz diferansiyel denklem;
𝑑
𝑥(𝑡) = 𝐴𝑥(𝑡) + 𝐵𝑒(𝑡)
𝑑𝑡
formatında bir denklemdir. Burada e(t) bağımsız kaynaklardır.
Bu denklemin çözümünde keyfi sabitler elde edilecektir. Bu sabitlerin bulunması için
devrenin çalışmaya başladığı 𝑡 = 0 anındaki değerleri olan ilk koşullar kullanılır.
Denklemin Homojen kısmının çözümüne öz çözüm denir. Be(t) teriminin de katkısı
eklendiğinde elde edilen çözüm zorlanmış çözüm, ve bu ikisinin toplamı tam çözüm olarak
adlandırılır.
Öz çözümün 𝑡 → ∞ için sıfır olduğu devreler asimptotik kararlı devreler olarak adlandırılır.
Asimptotik kararlı devrelerde devrenin incelenmeye başlanmasından kısa bir süre sonra tam
çözüm zorlanmış çözüme yaklaşık olarak eşit olacaktır ( Homojen kısmın etkisi sıfıra
yaklaşacaktır ). Geçici çözüm , başlangıçta çok büyük bile olsa, bir süre sonra sıfıra
yaklaşacaktır. Kalıcı çözüm devrede kaynaklar olduğu müddetçe devam eden çözümdür.
Şimdi, RL , RC ve RLC devrelerine kare dalga uygulanması halinde geçici çözümlerinin ne
olacağına bakalım.
6.2.2 Kapasitans Gerilim-Akım İlişkisi
İ (t)
+
C
V(t)
-
𝑖(𝑡) = 𝐶
𝑑𝑣(𝑡)
𝑑𝑡
Şekil 6.1. Kapasitans
Buradan gerilim değerini çekersek;
𝑡
1
𝑣(𝑡) = ∫ 𝑖(𝑡)𝑑𝑡
𝐶
−∞
Devrenin 𝑡 = 𝑡0 anında çalışmaya başladığını söylersek ;
𝑡
𝑡0
𝑡
∫ 𝑖(𝑡)𝑑𝑡 = ∫ 𝑖(𝑡)𝑑𝑡 + ∫ 𝑖(𝑡)𝑑𝑡
−∞
−∞
𝑡0
Sağdaki ilk terime 𝑡 = −∞ anından 𝑡 = 𝑡𝑜 anına kadar kapasitans üzerinde biriken yük 𝑣(𝑡0 )
denir. Öyleyse kapasitans gerilimi;
𝑣(𝑡) = 𝑣(𝑡0 ) +
1 𝑡
∫ 𝑖(𝑡)𝑑𝑡
𝐶 𝑡0
olur.
6.2.3. İndüktans Gerilim-Akım İlişkisi
İ (t)
+
L
V(t)
-
𝑣(𝑡) = 𝐿
Şekil 6.2. İndüktans
1 𝑡
𝑖(𝑡) = 𝑖(𝑡0 ) + ∫ 𝑣(𝑡)𝑑𝑡
𝐿 𝑡0
𝑑𝑖(𝑡)
𝑑𝑡
6.2.4. RC Devresi
Şekil 6.3.a’ daki RC devresine bakalım.
Şekil 6.3.a. RC devresi
Şekil 6.3.b. Kare Dalga
Bu devre için durum denklemleri;
𝑒(𝑡) = 𝑣𝑅 (𝑡) + 𝑣𝐶 (𝑡)
yazılır. Direnç ve kapasitans üzerinden aynı akım aktığından dolayı, kapasitans için akımgerilim ilişkisini göz önünde bulundurarak;
𝑑
1
1
𝑣𝐶 (𝑡) = −
𝑣𝐶 (𝑡) +
𝑒(𝑡)
𝑑𝑡
𝑅𝐶
𝑅𝐶
olarak devre denklemini yazarız. Kaynak gerilimi 𝑒(𝑡) = 𝐸 , 𝑡 < ∆ ve 𝑒(𝑡) = 0 , 𝑡 > ∆ için
ayrı ayrı analiz yapılmalıdır.
Diferansiyel denklemin çözümü; 𝑒(𝑡) = 𝐸 için,
𝑣𝐶𝑇𝐴𝑀 (𝑡) = 𝑣𝐶 (0)𝑒
−𝑡⁄
𝑅𝐶
+ 𝐸(1 − 𝑒
−𝑡⁄
𝑅𝐶 )
ve 𝑒(𝑡) = 0 için,
𝑣𝐶𝑇𝐴𝑀 (𝑡) = 𝑣𝐶 (∆)𝑒
−𝑡⁄
𝑅𝐶
şeklindedir.
Buradaki 𝑅𝐶 çarpımı zaman sabiti olarak adlandırılır ve 𝜏 ile gösterilir. Zaman sabiti öz
çözümün ne kadar süre geçerli olduğunu belirler. Öz çözümü belirleyen terimler 𝑣𝐶 (0)𝑒
ve 𝑣𝐶 (∆)𝑒
−𝑡⁄
𝑅𝐶
dır. 5𝜏 büyük değerler için 𝑒
−𝑡⁄
𝜏
−𝑡⁄
𝑅𝐶
< 0.01 olacağından öz çözümün sıfır olduğu
kabul edilir. Aynı şekilde zorlanmış çözüm de 𝐸(1 − 𝑒
−𝑡⁄
𝑅𝐶 )
ile ifade edildiğinden 5𝜏 zaman
sonra bu ifade 𝐸'ye yaklaşır. Bu kapasitenin dolmasıdır. Kaynak olmazsa kapasitans 5𝜏 zaman
sonra boşalacaktır. Kapasitansın dolma ve boşalma grafikleri aşağıdaki gibidir.
Şekil 6.4. Kapasitansın Dolma ve Boşalma grafikleri
Sekil 6.3.a’daki devreye Kirchhoff yasasını uygularsak 𝑣𝑅 (𝑡) gerilimini de bulabiliriz.
Aşağıdaki grafiklerde de kaynak, direnç ve kapasitansın gerilim değerlerinin değişimi
gözükmektedir.
Şekil 6.5. Kaynak,Direnç ve Kapasitansın Gerilim Değişimleri
6.2.5 RL DEVRESİ
Şekil 6.6’daki devre bir RL devresidir.
Şekil 6.6. RL Devresi
Bu devrenin durum denklemleri;
𝑑
𝑅
1
𝑖𝐿 (𝑡) = − 𝑖𝐿 (𝑡) + 𝑒(𝑡)
𝑑𝑡
𝐿
𝐿
şeklinde yazılır. RC devresinde yapılan durum analizleri RL devresi için de geçerlidir. Ancak
zaman sabiti 𝜏 = 𝐿⁄𝑅 dir.
6.2.6. RLC DEVRESİ
Aşağıdaki şekilde bir RLC devresi görülmektedir.
Şekil 6.7. RLC Devresi
Bu devrenin durum denklemleri şu şekildedir:
Bu denklem sisteminin karakteristik denklemi çözümün yapısını belirleyecektir. Bu
denklemin karakteristik denklemi aşağıdaki gibidir:
𝑝2 + 2𝜁𝑤0 𝑝 + 𝑤02 = 0
Burada;
dır. 𝜁'nın değerine göre denklemin kökleri aşağıdaki 3 halden biri şeklide olacaktır:
𝐿
a) 𝜁 > 1 ise 𝑅 > 2√𝐶 ve kökler reeldir.
𝐿
b) 𝜁 = 1 ise 𝑅 = 2√𝐶 ve kökler reel ve eşittir.
𝐿
c) 𝜁 < 1 ise 𝑅 < 2√𝐶 ve kökler kompleks eşleniktir.
𝑣𝐶 (0) = 0 ve 𝑖𝐿 (0) = 0 için her üç halde 𝑣𝐶 (𝑡)' nin zamanla değişimi aşağıda kabaca
çizilmiştir.
Şekil 6.8. 𝑣𝐶 (𝑡)' nin zamanla değişimi
6.3. Ön Çalışma
6.3.1. Bir RC devresi için 𝑅 = 10 Ω ve 𝐶 = 20µ𝐹 için zaman sabiti τ'yu bulunuz ve 𝑖(𝑡) =
2cos(5000𝑡) için 𝑣𝐶 (𝑡)′ yi bulunuz.
6.3.2. Bir RL devresi için 𝑅 = 470Ω ve 𝐿 = 40𝑚𝐻 için zaman sabiti τ'yu bulunuz ve 𝑣𝐿 (𝑡) =
3sin(300𝑡) için 𝑖(𝑡)′ yi bulunuz.
6.3.3. Bir RLC devresi için 𝑅 = 10Ω , 𝐿 = 27𝑚𝐻 ve 𝐶 = 380µ𝐹 değerleri için 𝐸 = 110𝑉 ve
𝑓 = 50 𝐻𝑧 iken indüktans akımı 𝑖𝐿 (𝑡) ve kapasitans gerilimi 𝑣𝐶 (𝑡) yi bulunuz.
6.4. İşlem Basamakları
6.4.1. Aşağıdaki şekildeki devreyi 100 Ω ve 1 µF ile kurunuz.
Şekil 6.9.

Devrenin girişine 0-5 V kare dalga uygulayınız.

Kare dalga osilatörünün frekansını değiştirerek kapasitans geriliminin değişimini
gözlemleyiniz.

Tam dolma, tam boşalma durumu frekansını belirleyiniz. Hesap ile bu değeri
doğrulayınız.

Kare dalga osilatörün periyodunu T = 10RC , T= RC ve T = RC/10 alarak, direnç ve
kapasitans gerilimlerini osiloskopta gördüğünüz şekilde çiziniz, tepe değerlerini
kaydediniz.
6.4.2. Kare dalga osilatörün genliğini yarıya düşürerek 6.4.1'deki ölçümleri tekrarlayınız ve
sonuçları yorumlayınız.
6.4.3. Aşağıdaki şekildeki devreyi 600 Ω ve 60 mH ile kurunuz.
Şekil 6.10.
Devrenin girişine 0-5 V kare dalga uygulayınız. Kare dalga osilatörünün frekansını
değiştirerek direnç geriliminin değişimini gözlemleyiniz. Tam dolma, tam boşalma durumu
frekansını belirleyiniz. Hesap ile bu değeri doğrulayınız. Kare dalga osilatörün periyodunu
T=10L/R , T=L/R ve T=L/10R alarak, direnç ve kapasitans gerilimlerini osiloskopta
gördüğünüz şekilde çiziniz, tepe değerlerini kaydediniz.
6.4.4. Aşağıdaki şekildeki devreyi 1 µF ve 60 mH ile kurunuz.
Şekil 6.11.
Devrenin girişine 100 Hz frekansında 0-5 V bir kare dalga uygulayınız. Ölçme düzeneğinde,
𝐿
𝑅 = 0.2√𝐶
𝐿
𝑅 = 2√𝐶
𝐿
ve 𝑅 = 20√𝐶 alarak, her bir hal için osiloskopta gördüğünüz dalga
𝐿
şekillerini çiziniz ve sonuçları yorumlayınız. 𝑅 = 20√ için kapasitansın değerini değiştiriniz
𝐶
ve bu değişimin dalga şeklini nasıl etkilediğini belirtiniz.
6.5. SONUÇ
6.5.1. Bu deneyden neler öğrendiniz?
7. DİYOT KARAKTERİSTİKLERİNİN BELİRLENMESİ
7.1. Deneyin Amaci
Bu deneyde diyotların akım-gerilim karakteristiği incelenecektir. Bir ölçü aleti ile (volt-ohm
metre) diyodun ölçülmesi ve kontrol edilmesi (anot ve katot terminallerinin saptanması).
Osiloskop kullanılarak farklı çeşitlerdeki diyodun akım-gerilim karakteristiğinin gözlenmesi.
7.2. Teorik Bilgi
7.2.1. PN Jonksiyon Diyot
Diyot bir yönde akımı diğer yöne göre daha iyi ileten, yarı iletken bir malzemedir. Diyot
terminalleri arasındaki potansiyel fark, diyodun iletime geçip geçmeyeceğini belirler. Eğer
anot katoda göre daha pozitif ise, diyot akımı iletecektir ve bu durumda diyot doğru
kutuplanmış demektir. Eğer katod anoda göre daha pozitif ise diyot çok küçük bir sızıntı
akımının geçmesine izin verecektir ve bu durumda diyot ters kutuplanmış demektir.
Şekil 7.1. Diyot devre sembolü
Doğru-kutuplamada, tipik bir Silikon diyot üzerinde düşen gerilim yaklaşık 0.7 V’tur
(Germanyum için ise gerilim düşümü 0.3 V’tur). Bu eşik gerilimi diyot karakteristik eğrisi
üzerinde büküm olarak adlandırılır. Çünkü bu bölgede diyot üzerinde düşen gerilimle diyottan
geçen akım değişmektedir. Bu eşik gerilim değerinin aşıldığı durumda iletim akımı “Id” akar.
Bu eşik geriliminden daha düşük değerlerde, diyot sadece küçük bir akımın geçmesine izin
verir. Diyodun ters kutuplanması halinde idealde diyotun akım iletmemesi gerekmektedir
fakat çok küçük bir sızıntı akımı akar bu akıma “Is” ters satürasyon akımı denir.
Diyot akım-gerilim ilişkisi aşağıdaki denklem ile modellenmektedir.
I D  I S eVD / nVT  1
Bu denklemde;
IS
: Ters satürasyon akımı
VD
: Diyota uygulanan gerilim
n
: İdealden uzaklaşma faktörü
VT
: Termal voltaj ( VT 
kT
) (oda sıcaklığında 26 mV civarıdır)
q
Şekil 7.2. Diyot akım-gerilim karakteristiği
7.2.2. Zener Diyot
Zener diyot jonksiyon diyodun özel bir tipidir. Zener diyot, doğru yönde bağlandığı zaman
normal bir diyot gibi çalışır; ters yönde bağlandığı zaman ise kırılma (zener) gerilimine kadar
iletime geçmez ama kırılma geriliminden sonra çığ etkisi şeklinde akım geçirir, yani zener
belirli bir gerilimden sonra iletime geçer. Ters gerilim kalkınca, zener diyot da normal haline
döner. Devrelerde, ters yönde çalışacak şekilde kullanılır. Şekil 7.3’te zener diyodun devre
sembolü ve akım-gerilim karakteristiği verilmiştir.
Şekil 7.3. Zener diyot devre sembolü ve akım-gerilim karakteristiği
7.2.3. Işık Yayan Diyot (LED)
Işık yayan diyot (LED) yarı-iletken, diyot temelli, ışık yayan bir elektronik devre elemanıdır.
LED’ler elektrik enerjisini optik enerjiye dönüştürürler. LED, P-N jonksiyonlu bir yarıiletken
olup iletim yönünde kutuplandığı takdirde ışık yayacak şekilde tasarlanmıştır. Bu ışık;
kırmızı, yeşil, sarı, ya da kızıl ötesi gibi çeşitli, renklerde olabilir. Normal diyot da olduğu gibi
LED’lerde de küçük değerde bir eşik gerilimi vardır. Bu eşik gerilimi aşıldığında jonksiyonun
direnci düşer ve akım iletmeye başlar. LED’lerin devrelerde kullanımında bu akım bir
dirençle sınırlandırılmalıdır. LED’in yaydığı ışık miktarı üzerinden geçen akıma bağlıdır.
LED devre sembolü ve akım-gerilim karakteristiği Şekil 7.4’te verilmiştir.
Şekil 7.4. LED devre sembolü ve akım-gerilim karakteristiği
7.2.4. Diyotların Test Edilmesi
Bir diyodun sağlam olup olmadığı veya terminalleri tanımlanamayan diyodun terminallerini
tanımlamak için bir ohmmetre kullanılabilir. Ayrıca sayısal (digital) multimetrelerin çoğunda
diyot test konumu da bulunmaktadır.
Diyodu test etmek için ölçü aleti ohmmetre modunda iken pozitif ucu (genellikle kırmızı
kablolu ucu) diyodun anoduna; negatif ucu (genellikle siyah kablolu ucu) diyodun katoduna
bağlanırsa diyot düz besleme durumunda bulunuyor demektir. Bu durumda diyodun direnci
oldukça küçük olmalıdır, pratik olarak sıfır direnç görülmektedir. Eğer ohmmetrenin pozitif
ucu diyodun katoduna, negatif ucu anoduna bağlanırsa, diyot ters besleme durumundadır ve
ohmmetre çok büyük direnç göstermelidir. Pratik olarak bu değerin sonsuz olması gerekir.
Eğer bir ohmmetrenin uçları diyota her iki türde bağlandığında ohmmetre her iki yönde de
çok büyük direnç veya çok küçük direnç gösteriyorsa bu diyot görev yapmıyor demektir.
Şekil 7.5. Diyotların test edilerek terminallerinin belirlenmesi
Sayısal (digital) multimetrelerde diyot test kademesi kullanılarak diyot test edilebilmektedir.
Bu kademede yapılan ölçümde görünen değer direnç yerine diyodun ileri geçirimde üzerinde
düşen gerilimin değeridir. Diyodun üzerinden küçük bir akım geçirilir ve iki ölçüm ucu
arasındaki gerilim farkı ekranda gösterilir. Şekil 7.6’da “Diyot test” kademesinde yapılan bir
ölçümde diyodun ileri geçirimde 0,548 Volt düşürdüğünü görüyoruz.
Şekil 7.6. Multimetre test kademesi kullanılarak diyotun test edilmesi
7.2.5. Diyotların i-v Karakteristiğinin Elde Edilmesi
Diyodun i-v karakteristiğini elde edebilmek için Şekil 7.7’deki devre oluşturularak X ve Y ile
ifade edilen uçlara osiloskop bağlanarak ölçümle analiz edilir.
Şekil 7.7. Diyodun i-v karakteristiğinin elde edileceği örnek devre
Bu devrede “R” direnci diyot üzerinden geçen akımı sınırlamak amacıyla kullanılmaktadır.
Osiloskop direk olarak akım ölçemeyeceğinden 10 Ω değerindeki direnç seri bağlanarak
üzerine düşen gerilim hesaplanır ve bu gerilimin dirence bölünmesiyle akım elde edilir.
X-ucunda görülen gerilim diyot ve 10 Ω’luk direnç gerilimlerinin toplamına eşittir. Eğer 10 Ω
değerindeki direnç üzerine düşen gerilim diyot üzerindeki gerilimle kıyaslandığında çok
küçükse, X-ucunda görülen gerilim yaklaşık olarak diyot üzerindeki gerilime eşit olacaktır. R
and Vs değerleri diyodun arızalanmaması ve işlevini yitirmemesi açısından dikkatli biçimde
seçilmelidir. Bu nedenle, eğer diyot doğrultucu devresinden geçen maksimum akım Imax 1A
ise
VS  V
R  10
 1 olacağından VS = 20sinwt V ve 𝑅=5Ω değerlerini diyodun zarar
görebileceğinden dolayı veremeyiz. Sağlıklı bir devrede |VS|>>0.7 V olarak belirlenmelidir.
Tablo 7.1. Üç farklı diyot çeşidi için özellikler
7.3. Ön Çalışma
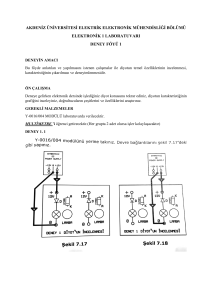
7.3.1. Deneye gelmeden önce Şekil 7.7’de ifade edilen devreyi sırasıyla 1N4001, MV5353 ve
BZX8506V diyotları akım-gerilim karakteristiklerini elde ediniz.
7.4. İşlem Basamakları
7.4.1. Deneyde Kullanılacak Malzemeler:
Direnç : 10Ω, 1 kΩ
Doğrultucu Diyot : 1N4001
LED : MV5353
Zener Diyot : BZX8506V2 (6.2 V)
Standart Laboratuvar Ekipmanları:
Osiloskop, DC Güç Kaynağı, Sinyal Jeneratörü, Dijital Multimetre, Protoboard,
7.4.2. Diyot Testi: Diyotları 6.2.4. bölümde anlatılan kurallara uygun biçimde Dijital
Multimetre ile test ediniz.
7.4.3. Diyodun i-v Karakteristiğinin Çıkarılması: Tablo 7.1’de deneyde kullanılan farklı
diyot tipleri için özellikler verilmiştir. Şekil 7.7’de verilen devreyi
VS  10sin(2100t )
ve
𝑅=1kΩ olacak şekilde kurun ve sırasıyla pn Jonksiyon diyot, LED ve Zener diyot için akımgerilim (i-v) karakteristiklerini gözlemleyin.
7.4.4. Karakteristik Eğrilerini Kullanarak aşağıdaki tabloyu doldurunuz.
7.5. SONUÇ
7.5.1. Teorik ve deneysel sonuçları karşılaştırınız. Eğer farklılık varsa nedenlerini açıklayınız.
7.5.2. Bu deneyden neler öğrendiniz?
7.5.3. Terminalleri işaretlenmemiş bir diyotun anotunu nasıl anlayabilirsiniz?
7.5.4. Hangi koşullarda bir jonksiyon diyot iletime geçer? Açıklayınız.
8. DİYOT DOĞRULTUCU DEVRELERİ
8.1. Deneyin Amaci
Bu deneyde elektronik dc güç kaynaklarının ilk aşaması olan diyot doğrultucu devreleri test
edilecektir. Deneyin amacı; doğrultucu devrelerin (yarım ve tam dalga doğrultucunun)
çalışma prensibinin kavranması ve doğrultucu çıkışındaki dalgalanmayı (ripple) azaltmak için
kullanılan kondansatörün etkisinin incelenmesidir.
8.2. Teorik Bilgi
Radyo, Televizyon, Masaüstü Bilgisayar gibi birçok elektronik cihaz içerdikleri elektronik
devrelerin çalışabilmesi için bir dc güç kaynağına gereksinim duyarlar. DC güç kaynakları
doğrultucu devreler kullanılarak dizayn edilebilirler. Doğrultucu devreler alternatif akım (AC)
sinyalini doğru akım (DC) sinyaline dönüştürebilen devrelerdir. Doğrultucu devreler idealde
ileri iletimdeyken kapalı bir anahtar gibi, ters iletimde ise açık anahtar gibi davranırlar. Buna
bağlı olarak AC akımı DC akıma dönüştürmede çok kullanışlı devrelerdir. Temel olarak iki
ana doğrultucu devre konfigürasyonu vardır: Yarım Dalga Doğrultucu Devre ve Tam Dalga
Doğrultucu Devre.
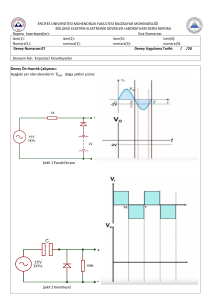
8.2.1. Yarım Dalga Doğrultucu Devre
Yarım dalga doğrultucu devresi Şekil 8.1 (a)’da gösterilmektedir. Giriş sinyalinin pozitif
yarım
periyodunda, diyot ileri iletimde olacaktır. Dolayısıyla çıkış gerilimi yalnızca AC giriş
sinyalinin
pozitif yarım periyodunda görünecektir. Negatif yarım periyotta diyot ters iletimde
olacağından açık anahtar gibi davranacağından üzerinden akım geçirmeyecek, dolayısıyla
çıkış gerilimi sıfıra eşit olacaktır. Yarım dalga doğrultucu devrede görülen giriş ve çıkış
sinyali
Şekil 8.1 (b)’de görülmektedir. Bu devrede diyotun ideal olduğu kabul edilirse, DC çıkış
gerilimi;
V0 dc 
Vm

Şekil 8.1. Yarım Dalga Doğrultucu (a) devresi, (b) AC giriş sinyali (Vin) ve çıkış sinyali (Vo)
8.2.2. Tam Dalga Doğrultucu Devre
Çıkış geriliminin, giriş sinyalinin hem pozitif hem de negatif yarım periyodunda görüldüğü
devreler Tam Dalga Doğrultucu devreler olarak isimlendirilirler. Tam Dalga Doğrultucu
devreler iki farklı şekilde oluşturulabilirler: Ortası Sıfırlanmış Doğrultucu ve Köprü
Doğrultucu
 Ortası Sıfırlanmış Doğrultucu: Tam Dalga Ortası Sıfırlanmış Doğrultucu devre ve
giriş-çıkış sinyallerinin dalga formları Şekil 8.2’de görülmektedir. Trafonun sekonder sargısı,
iki eşit giriş gerilimi (Vin) elde edebilmek için orta noktasından topraklanmıştır. Trafonun
seconder sargısının orta noktası topraklandığından dolayı devre iki yarım dalga doğrultucu
devreye eşit olur. D1 diyotu giriş gerilim sinyali pozitifte iken iletimde olurken D2 diyotu da
giriş gerilim sinyalinin negatifte olduğu zaman iletimde olacaktır. Buna bağlı olarak
doğrultulan yük akımı her iki yarım periyotta da akacaktır ve çıkış gerilimi her iki yarım
periyotta da giriş gerilimine eşit olacaktır.
Şekil 8.2. Tam dalga Ortası Sıfırlanmış Doğrultucu devre ve giriş-çıkış gerilim dalga formları
 Köprü Doğrultucu: Tam Dalga Köprü Doğrultucu devre ve giriş-çıkış sinyallerinin
dalga formları Şekil 8.3’de görülmektedir. Giriş geriliminin pozitif yarım periyodunda D2 ve
D4 diyotları ileri iletimde olacak ve kapalı anahtar gibi davranacak, D1 ve D3 ise kesimde
olacağından açık anahtar gibi davranacaktır. Akım D2 ve D4 diyotları üzerinden akacak, yük
direnci pozitif bir çıkış gerilimi oluşturacaktır. Giriş geriliminin negatif yarım periyodunda
D1 ve D3 diyotları ileri iletimde olacak ve kapalı anahtar gibi davranacak, D2 ve D4 ise
kesimde olacağından açık anahtar gibi davranacaktır. Akım D2 ve D4 diyotları üzerinden
akacak, yük direnci yine benzer şekilde pozitif bir çıkış gerilimi oluşturacaktır.
Şekil 8.3. Tam Dalga Köprü Doğrultucu devre ve giriş-çıkış gerilim dalga formları
Diyotların ideal olduğu kabul edilirse, tam dalga doğrultucunun DC çıkış gerilimi;
V0 dc 
2Vm

Tam dalga doğrultucunun DC çıkış gerilimi, yarım dalga doğrultucunun DC çıkış geriliminin
iki katına eşit olacaktır.
8.2.3. Filtreler ve Çıkış Gerilim Dalgalanması
Güç kaynaklarında en önemli nokta, doğrultulmuş çıkışın gerilim dalgalanmasını minimum
indirmektir. Dalgalanmanın azalması amacıyla filtrelenme işlemi yapılır. En basit haliyle bir
filtre devresi Şekil 8.4’te görüldüğü gibi doğrultucuya paralel olarak bağlanmış bir
kondansatörden oluşur.
Şekil 8.4. Filtre kapasitörü içeren Yarım Dalga Doğrultucu devre ve giriş-çıkış gerilim dalga formları
Diyot ideal kabul edilirse, filtre kapasitörü içeren yarım dalga doğrultucu devrenin DC çıkış
gerilimi;
V0 dc 
Vm
1
1
2 fCR
Çıkış geriliminde görülen dalgalanma;
V 
V0 dc
2 fCR
Filtre kapasitörü içeren Tam Dalga Köprü Doğrultucu devre ve giriş-çıkış sinyallerinin dalga
formları Şekil 8.5’te görülmektedir. Diyotlar ideal kabul edilirse, çıkış gerilimi;
V 0dc 
Vm
1
1
4 fCR
Çıkış geriliminde görülen dalgalanma;
V 
V0 dc
2 fCR
Şekil 8.5. Filtre Kapasitörü içeren Tam Dalga Köprü doğrultucu devresi ve çıkış dalga formu
8.2.4. Gerilim Katlayıcı Devre
Tam Dalga Doğrultucu devrede iki diyot, iki kapasitör ile yer değiştirilerek oluşturulan devre
“Gerilim Katlayıcı Devre” ismini alır ve bu devrede görülen çıkış gerilimi yaklaşık olarak
trafonun tepe geriliminin iki katına eşit olur. Şekil 8.6’da Gerilim Katlayıcı Devresi
verilmektedir.
Tek bir AC gerilimden güç trafosu yardımıyla çoklu DC gerilimler üretilebilir.
Şekil 8.6. Gerilim Katlayıcı Devre
8.3. Ön Çalışma
8.3.1. Teorik Hesaplamalar yaparak denklemler 8.3, 8.4, 8.5 ve 8.6’yı elde ediniz.
8.3.3. Şekil 8.4 ve Şekil 8.5’te verilen devreleri kullanarak Vodc ve Vrpp bulunuz,
bulduğunuz değerlere göre aşağıdaki tabloyu doldurunuz.
Şekil 8.4 için
Şekil 8.5 için
8.4. İŞLEM BASAMAKLARI
8.4.1. Deneyde Kullanılacak Malzemeler:
Direnç
: 2.2 kΩ
Doğrultucu Diyot
: 4 X 1N4001
Kapasitörler
: 2 X 10 μF, 470 μF
Standart Laboratuvar Ekipmanları:
Osiloskop, DC Güç Kaynağı, Sinyal Jeneratörü, Dijital Multimetre, Protoboard
Dikkat Ediniz
: Tam Dalga Doğrultucu devrede Osiloskop kullanarak aynı anda giriş
ve çıkış dalga formunu ölçmeyi denemeyiniz.
8.4.2. Şekil 8.4’te verilen devreyi laboratuvarda kurun, çıkış geriliminin zamana bağlı
grafiğini aşağıdaki durumlar için elde edin.
8.4.3. Şekil 8.5’te verilen devreyi laboratuvarda kurun, çıkış geriliminin zamana bağlı
grafiğini aşağıdaki durumlar için elde edin.
8.4.4. Çıkış gerilim dalga formlarını kullanarak aşağıdaki tabloyu doldurunuz.
8.4.5. Şekil 8.6’daki devreyi laboratuvarda kurarak çıkış geriliminin zamana bağlı grafiğini
aşağıdaki durumlar için elde ediniz.
8.5. SONUÇ
8.5.5. Ön Çalışma neticesinde elde ettiğiniz teorik hesaplama ve simülasyon sonuçları ile
deneysel sonuçları karşılaştırınız. Eğer farklılık varsa nedenlerini açıklayınız.
8.5.6. Yarım Dalga Doğrultucu devre ile Tam Dalga Doğrultucu devre sonuçlarını
karşılaştırınız. Hangisinin daha iyi sonuçlar ürettiğini nedeni ile belirtiniz.
8.5.7. Doğrultucu devrelerin hangi alanlarda ve ne amaçla kullanıldığını açıklayınız.
9. İKİ KUTUPLU JONKSİYON TRANSİSTÖR (BJT - BIPOLAR JUNCTION
TRANSISTOR)
9.1. Deneyin Amaci
Bu deneyde iki kutuplu eklem transistörlerin (BJT) ve temel iki kutuplu eklem transistörlü
yükselteçlerin akım-gerilim karakteristiği çıkartılacaktır. Aynı zamanda BJT’nin h değişkeni
saptanacaktır.
9.2. Teorik Bilgi
Transistörler üç bacaklı bir devre elemanıdır, akım veya gerilim yükselteci olarak ya da
anahtarlama elemanı olarak kullanılır. BJT’lerin bir bacağından geçen akım diğer iki bacak
arasındaki gerilim ile kontrol edilir.
İki kutuplu eklem transistörlerin(BJT) n bölgesiyle ayrılmış iki p bölgesinden (PNP) ya da p
bölgesi ile ayrılmış iki n bölgesinden (NPN) oluşur. NPN ve PNP tip BJT’lerin basitleştirilmiş
yapısı ve devre sembolü Şekil 9.1’de gösterilmiştir.
Şekil 9.1. NPN ve PNP Tip BJT’lerin Basitleştirilmiş Yapısı ve Devre Sembolleri
BJT’ler dört modda çalıştırılabilirler. Bunlar kesim, doyum, ileri aktif ve geri aktifdir. Eğer
BJT yükselteç olarak kullanılmak isteniyorsa, ileri aktif modda çalıştırılmalıdır. Bu da B-E
eklemini ileri öngerilimlendirme ve B-C eklemini ters ön gerilimlendirme yaparak
sağlanabilir. BJT’nin ileri aktif moda çalıştırılabilmesi için iki harici gerilim kaynağına
ihtiyaç vardır. NPN BJT’nin akımları Şekil 9.2’de gösterilmiştir.
Şekil 9.2. NPN İki Kutuplu Transistörün Akımları
Eğer transistör ileri aktif moda ise, toplayıcı akımı;
VBE
I C  I S e T
IS doyum akımı, φT ısıl gerilim ve VBE B-E bacakları arasındaki gerilimdir. Taban akımı ise;
IB 
IC


IS

VBE
e T
olarak bulunur. β toplayıcı-yayıcı akım kazancıdır. Bu durumda yayıcı akımı;
I E  IC  I B
B-E arasındaki gerilimi sıfır (VBE = 0) yaptığımız zaman transistör kesim modunda olur, fakat
B-C eklemi ters öngerilimlendirilir. Bu ters öngerilimlendirmeden dolayı, B-C ekleminden bir
sızıntı akımı(ICBO) akar. Eğer ideal olmayan transistörlerdeki bu sızıntı akımının etkisi hesaba
alınırsa, toplayıcı akımı;
I C   I   (1   ) I CBO
Şekil 9.3’te ortak-yayıcı devrenin IC-VCE karakteristiği gösterilmiştir. Şekil 9.4’te ise bu
karakteristiğin elde edildiği devre şeması gösterilmiştir.
Şekil 9.3. Ortak-Yayıcı Devrenin Transistör Akım-Gerilim Karakteristiği
Şekil 9.4. Ortak-Yayıcı Devrenin Trasistör Akım-Gerilim Karakteristiğinin Elde Edildiği Devre
9.2.2. İki Kutuplu Eklem Transistörlerin h Değişkeni
BJT’nin küçük işaret hibrid eşdeğer devre modeli Şekil 9.5’te gösterilmiştir.
Şekil 9.5. Ortak-Yayıcı Yükselteç Devresi
h değişkeni Şekil 9.3’te IC-VCE karakteristiğinden bulunur. h değişkeni;
h fe   
I CQ
I BQ
hfe küçük işaret akım kazancıdır. ICQ çalışma noktasındaki toplayıcı akımı, IBQ yine çalışma
noktasındaki taban akımıdır.
hie 
T
I BQ
hie küçük işaret giriş direncidir. φT ısıl gerilimdir ve oda sıcaklığında yaklaşık olarak 26
mV’dur. Küçük işaret çıkış direnci (hoe)
hoe 
I CQ
VA
olarak hesaplanır. VA Early gerilimdir. hoe IC-VCE karakteristiğinin eğiminden elde edilebilir.
9.3. Ön Çalışma
Vγ = 0.6 V, R1=100 kΩ, R2= 10 Ω için;

C 3146’nın veri föyünü kullanarak BJT’nin ICQ=1 mA,ve VCQ=5 V çalışma
noktasındaki h değişkenlerini bulunuz. Tablo 8.1’ i doldurunuz.
9.4. İşlem Basamakları
9.4.1. Deneyde kullanılacak Malzemeler
Direnç : 10 Ω, 100 kΩ.
IC : CA3146
Diyot : 1N4001
Standart Laboratuvar Ekipmanları:
Osiloskop, DC Güç Kaynağı, Sinyal Jeneratörü, Dijital Multimetre, Protoboard
R1=100 kΩ, R2= 10 Ω, VBB=0 V, 2 V,4 V, 6 V, 8 V ve VS=10sin(2π100t)
Şekil 9.6. BC 237 Transistörünün Bacak Numaraları
9.4.2. BJT’yi DMM ile test ediniz. R1’i DMM ile ölçünüz ve değerini Tablo 9.1’e yazınız.
9.4.3. Şekil 9.4’teki devreyi kurunuz ve IC-VCE karkteristiğini gözlemleyiniz ve çiziniz.
9.4.4. VBB gerilimini ICQ=1 mA ve VCQ=5 V için geçerli değere ayarlayıp basamak 9.4.3’ü
tekrar ediniz. IBQ, hfe ve hie’yi ölçünüz ve Tablo 9.1’e yazınız.
9.5. Sonuç
9.5.1. Ön Çalışma sonuçları ile deney sonuçlarını karşılaştırınız, farklar varsa nedenini
açıklayınız