10.1
10.2
İş
Virtüel İş İlkesi
Örnekler
10.3 Potansiyel Enerji
Örnek
PROBLEMLER
161
163
165
168
169
170
10.1 İŞ
Bir taşıyıcı sistemde, bağ koşullarına sadık kalacak biçimde, bir takım
küçük hareketler yaptırabildiğimizi varsayalım. O zaman bu tip sistemleri
çözmek için, denge denklemlerini ( F = 0 ve M = 0 ) kullanmak yerine, kuvvet ve kuvvet çiftlerinin yapacağı işi hesaplayarak sonuçlara ulaşmak bazen daha basit olabilir.
Çok parçalı bir sistem iş metodu ile çözülecekse, onu tek bir parça olarak
ele alıp, sistemin enerjisini tanımlamak gerekir. Bir işin ortaya çıkması
için en az bir kuvvet ve ona bağlı bir yer değiştirmenin aynı anda olması
gerekir. Şekil (10.1) de F kuvveti etkisinde, konumu r vektörüyle tanımlanmış P bir parçacığını ele alalım ve onun üstünde yapılan işi hesaplayalım.
Bir Kuvvetin İşi: Bir cismi bir noktadan bir başka noktaya hareket ettiren
her kuvvet sonuç cisim üstünde bir iş yapar. Bu durumda Şekil (10.1)
deki P parçacığı üstünde yapılan iş,
dU = F ⋅ dr
(10.1)
biçiminde hesaplanır ve skaler çarpım işleminden,
dU = F ds cos
(10.2)
yazılır. (10.2) de görüldüğü gibi iş skaler bir büyüklüktür. Burada açısı;
F ve dr vektörleri arasında ölçülür. (10.2) de F > 0 ve ds > 0 olmak
koşuluyla,
0 £ < 12
= 12
için dU > 0
için dU = 0
1
2
için dU < 0
< £
ü
ï
ï
ï
ï
ý
ï
ï
ï
ï
þ
(10.3)
dır. (10.1) deki vektörlerin bileşenleri,
F = Fx i + Fy j + Fz k
dr = d xi + d y j + d z k
ü
ï
ï
ý
ï
ï
þ
(10.4)
dir (Bakınız Şekil 10.1). dU = F ⋅ dr de (10.4) yerleştirilip skaler çarpım
işlemi yapıldıktan sonra ifade integre edilirse, F kuvvetinin işi,
U = ò ( Fx dx + Fy dy + Fz dz )
L
elde edilir.
(10.5)
162
STATİK ve MUKAVEMET
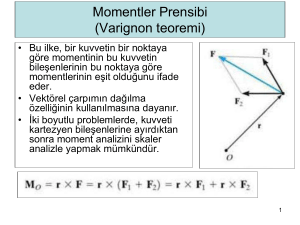
Bir Kuvvet Çiftinin İşi: şekil (10.2) deki kuvvet çifti (F, - F ) ye eşdeğer
moment M = (2 r ) ´ F , cisimde dönmeye sebep oluyorsa, o zaman bu
moment bir iş yapar. Şekil (10.2) de kuvvet çiftine eşdeğer momentin işi,
dU = M ⋅ dθ
(10.6)
dir. Bu ifade, skaler çarpım sonucu,
dU = M d cos
(10.7)
olur. Burada açısı, Şekil (10.2) de görüldüğü gibi moment vektörü M
ile dönme vektörü dθ arasında ölçülür. (10.6) deki eşitliğin sağındaki
terimler, bileşenleri cinsinden,
M = M xi + M y j + M zk
dθ = d x i + d y j + d z k
ïüï
ý
ïï
þ
(10.8)
dir. (10.6) de (10.8) yerleştirilip, skaler çarpım işleminden sonra ifade
integre edilirse, M momentinin işi,
U = ò ( M x d x + M y d y + M z d z )
(10.9)
elde edilir.
Şimdi önemli soru "Her kuvvet bir iş yapar mı?" nın cevabı, "İç kuvvetler
ile sabit mesnetlere ait bağ kuvvetleri iş yapmaz" diye verilir. Bunun için
çok sık karşılaşılan iki örnek verelim. Şekil (10.3) deki G mafsalındaki
bağ kuvvetleri Gx ile Gy etkitepki kuralına göre birbirlerini dengelerler
ve yapacakları pozitif ve negatif işlerin toplamı sıfır olur. Benzer biçimde
Şekil (10.4) deki ve cisimlerini bir sürtünmesiz makara yardımıyla
birbirlerine bağlayan kablodaki kablo kuvveti de bir iç kuvvet olduğu için
o da hiç bir iş yapmaz.