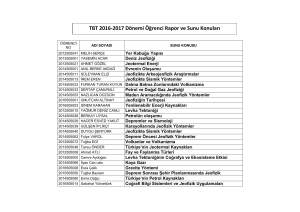
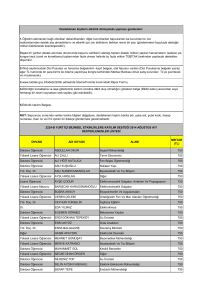
Elektromanyetik Teori Bahar 2005-2006 Dönemi
MANYETOSTATİK (1)
Giriş
Manyetizma, belirli bazı taşların (manyetit), demir tozlarını çekmesini gözlenmesiyle
başlamıştır. Manyetizma sözcüğü ise, bu taşların bolca bulunduğu Manisa yöresinden
kaynaklanır. Bu bölümde manyetik alanla ilgileneceğiz. Bilindiği gibi dünyanın
manyetik alanı vardır ve bu alan pusula ibrelerini saptırır. İçinden akım geçen bir telin
pusula ibresini saptırdığı, ilk defa 1820 de Hans Christian Orstead tarafından
gözlenmiştir. Bu gözlem, fizik tarihinin önemli deneylerinden biridir. İlk defa,
elektrik ile manyetizma arasında bir ilişki olduğu anlaşılmıştır. Bu önemli buluşa
kadar, elektrik ve manyetizma birbirinden ayrı iki bilim dalı gibi gelişim göstermiştir.
Durgun elektriğe ait özellikleri incelerken, iki yükün karşılıklı olarak birbirlerine bir
kuvvet uyguladığı ve bu kuvvetin
Yük ↔ Elektrik alan ↔ Yük
modeline uygun olarak ortaya çıktığını incelemiştik. Bu etkileşme teorisinde elektrik
alan bir ara ortam görevi yapar. Bu modele göre yük çevresinde elektrik alan
oluşmakta ve diğer yükün etkileşmesi sonucu kuvvet ortaya çıkmaktadır.
Elektrik alandaki bu yük elektrik alan modeline benzer şekilde manyetik alan için
Akım ↔ Manyetik alan ↔ Akım
modeli yazılabilir.
Elektrik alanda incelediğimiz E ve D vektörlerine benzer iki vektör de manyetik alan
için vardır. Bu vektörleri H ve B ile göstereceğiz. Ayrıca elektrik alan için yazdığımız
D = ε 0 E bağıntısına benzer B = μ 0 H bağıntısı vardır. Burada H (A/m) için
2
manyetik alan şiddeti veya sadece manyetik alan diyeceğiz. B (Webers / m ) ise
manyetik akı yoğunluğudur. Genellikle B nin birimi webers/alan yerine gauss veya
tesla kullanılır. Burada biz B nin birimi için tesla ve H nin birimi için Amper/m
kullanacağız. μ 0 sabitine manyetik geçirgenlik denir. Bu sabit elektrikte ε 0 sabitine
benzer. İlki boşluğun manyetik özelliğini, sonraki ortamın elektrik özelliği ile
−7
ilgilidir. Boşluğun manyetik geçirgenliği μ 0 = 4π × 10
ve birimi Henry/m veya
kısaca H/m dir.
Biot-Savart Yasası
Biot Savart yasası elektrostatikteki Coulomb yasasına benzerdir. Biot-Savart yasasına
göre herhangi bir P noktasındaki, manyetik alan şiddeti dH, diferansiyel akım elemanı
tel ile nokta arasındaki açıyla doğru orantılı aralarındaki uzaklığın karesiyle ters
orantılı olduğunu ifade eder (Şekil 1). Bu formüllerle ifade edilirse,
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
1
Elektromanyetik Teori Bahar 2005-2006 Dönemi
dH ∝
dH =
Idl sin α
R2
Idl sin α
(1)
4πR 2
yazılabilir. (1) bağıntısı aynı zamanda vektör çarpım şeklinde aşağıdaki şekilde
dH =
Idl × a R Idl × R
=
(2)
4πR 2
4πR 3
gösterilebilir. Burada R = R ve a R = R
R
dır. Vektör çarpımdan hatırlayacağınız
dl
R
P
dH (Sayfa içine doğru)
x
α
I
Şekil 1. Idl akım elemanından dolayı P noktasındaki manyetik alan.
gibi dH nin yönü sağ el kuralına göre bulunur. Burada yönden kasıt, manyetik alanın
kuzeyi gösterdiği yöndür (pusulanın N kuzey ucu). (2) denklemi çizgisel akım için L
boyunca
Idl × a R
(3)
2
L 4πR
H=∫
ile hesaplanır.
Şekil 2 de manyetik alanının yönü için kullanılan semboller gösterilmiştir.
dH (Sayfa dışına doğru)
.
(a)
dH (Sayfa içine doğru)
x
(b)
Şekil 2. Manyetik alanın (kuzeyi) yönü, (a) sayfa dışına doğru (b) sayfa içine doğru.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
2
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Akım geçen teli elimizle tuttuğumuzda baş parmak akım yönünü göstermek koşuluyla
diğer dört parmağın gösterdiği yön dH nin yönüdür (Şekil 3).
I
dH
I
tel
el
dH
Şekil 3. Bir telden geçen akım ve sağ el kuralıyla manyetik alanın yönünün
bulunması.
Örnek:
Şekil 4 te gösterildiği gibi akım geçen bir telden (A ve B noktaları arasında z
boyunca uzanan tel) R kadar uzaklıkta bir P noktasında manyetik alanı (3) bağıntısı
kullanarak hesaplayalım.
Çözüm:
P( ρ ,0,0) ve dl(0,0,z) nokta koordinatları göz önünde tutulursa R
R = ( ρ − 0) a ρ + ( 0 − 0) a φ + ( 0 − z ) a z
R = ρa ρ − za z
ve
dl = dza z
buradan
aρ
dl × R = 0
aφ
0
az
dz = ρdza φ
ρ
0
−z
olur. Bu ifadeleri
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
3
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Idl × R
3
L 4πR
H=∫
integral bağıntısında yerine koyarsak
H=∫
Iρdz
4π [ρ + z
2
2
]
3
2
a φ (4)
yazılabilir. Şekil 4 ten görülebileceği gibi cot α = z
ρ ⇒ z = ρ cot α dır. Bu
2
2
2
ifadenin türevini alırsak dz = − ρ cos ec αdα olur. Ayrıca cos ec α = 1 + cot α
ve cos ecα = 1
eşitlikleri hatırlanır ve bunları (4) te yerine konulursa, yeni
sin α
ifadenin integrali alındığında
α
I α ρ 2 cos ec 2αdα
I α ρ 2 cos ec 2αdα
I
H=−
aφ = −
aφ = −
a φ ∫ sin αdα
3
∫
∫
4π α [ρ 2 + ρ 2 cot 2 α ] 2
4π α ρ 3 cos ec 3α
4πρ α
=−
I
4πρ
2
2
2
1
1
1
α2
a φ (− cos α ) α =
1
I
α2
4πρ
H=
a φ (cosα ) α =
1
I
4πρ
I
4πρ
(cosα 2 − cos α 1 )a φ
(cosα 2 − cos α 1 )a φ (5)
olarak bulunur.
z
B
α2
dl
z
I
A
O
α
R
α1
P
ρ
x
H
Şekil 4. Çizgisel akımın P noktasında oluşturduğu manyetik alan.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
4
Elektromanyetik Teori Bahar 2005-2006 Dönemi
(5) bağıntısı A ve B noktaları sonsuz olduğunda değerlendirelim. A nın koordinatı
0(0,0,0) ve B (0,0, ∞) olsun bu durumda
α 1 = 90 o
α 2 = 0o
olur. Bu durumda (5) bağıntısı
H=
I
4πρ
aφ
olur. Benzer şekilde A ve B noktalarının koordinatları A(0,0,−∞) ve B (0,0, ∞)
olduğunda
α 1 = 180 o
α 2 = 0o
olur. Tekrara (5) bağıntısında bu değerler yerine konulursa
H=
I
2πρ
aφ
elde edilir.
(3) integral ifadesi çizgisel akım için geçerlidir. Eğer alansal veya hacimsel akımdan
dolayı oluşan manyetik alan hesap edilmek isteniyorsa, bu durumda, yüzeysel akım için
KdS × a R
(6)
4πR 2
S
H=∫
hacimsel akım için
Jdv × a R
(7)
4πR 2
V
H=∫
bağıntıları yazılır.
Örnek:
Çember şeklinde bir halkanın koordinatları x + y = 9 ve z=0. Halkaya 10 A doğru
2
2
akım uygulanmaktadır. Akımın yönü aφ dir. Verilenlere göre H nin (0,0,4) ve (0,0,-4)
değerini bulunuz?
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
5
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Çözüm:
Şekil 5 te problemin şekli çizilmiştir. Problemi çözmek için Biot-Savart yasasını yazalım
Idl × a R Idl × R
=
(8)
4πR 2
4πR 3
dl = ρdφa φ (9)
R = (0,0, h)-( ρ ,0,0) = − ρa ρ + ha z (10)
dH =
R = ρ 2 + h 2 (11)
(9) ve (10) ifadelerinden
aρ
dl × R = 0
−ρ
aφ
ρdφ
0
az
0 = ρhdφa ρ + ρ 2 dφa z (12)
h
bulunur. (11) ve (12) yi (8) de yerine yazalım
dH =
I
4π [ρ 2 + h 2 ] 2
dH =
3
I
4π [ρ + h
2
2
]
3
(ρhdφa
2
(dH
ρ
ρ
+ ρ 2 dφa z )
a ρ + dH z a z )
Şekil 5 ten görüleceği gibi, manyetik alanın iki bileşeni vardır. Bunlardan yatay olan
sıfırdır. P noktası etrafında 180 derece döndürdüğümüzde, bu vektörlerin toplamı
birbirlerini yok eder, bu durum problemin simetrisinden kaynaklanır. Sonuç olarak
hesaplanması gereken sadece düşey, z yönündeki bileşendir.
Bu durumu matematiksel olarak şu şekilde gösterebiliriz.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
6
Elektromanyetik Teori Bahar 2005-2006 Dönemi
z
dHz
P(0,0,h)
dHρ
R
y
ρ
dl
I
x
Şekil 5. Çember şeklinde bir halkadan geçen akım ve ekseni üzerindeki bir P
noktasındaki manyetik alan.
dH ρ =
dH ρ =
Iρhdφ
4π [ρ + h
2
2
]
2
2
]
2
Iρhdφ
4π [ρ + h
2
3
3
aρ
(cosφa
x
+ sin φa y )
bu son ifadenin 0 ≤ φ ≤ 2π aralığında integrali alınırsa
H = ∫ dH ρ = ∫
=
Iρhdφ
4π [ρ 2 + h 2 ] 2
3
(cosφa
x
+ sin φa y )
Iρh
2π
⎛ 2π
⎞
+
cos
φ
d
φ
a
sin φdφa y ⎟
x
3 ⎜ ∫
∫
0
⎠
4π [ρ 2 + h 2 ] 2 ⎝ 0
=0
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
7
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Probleme tekrar dönelim ve dHz bileşenini hesaplayalım.
dH z =
Iρ 2 dφ
4π [ρ 2 + h 2 ] 2
3
H = ∫ dH z =
H=
2[ρ
0
Iρ 2
2
Iρ 2 dφ
2π
∫
+h
2
az
4π [ρ 2 + h 2 ] 2
3
]
3
2
az =
Iρ 2 2π
4π [ρ 2 + h 2 ] 2
3
az
a z (13)
olarak bulunur. Son bulunan bağıntıda
I = 10 A
ρ 2 = x2 + y2 = 9
ρ =3
h=4
verilenler yerine yazılırsa
H(0,0,4) =
Iρ 2
2[ρ 2 + h 2 ] 2
3
10(3)
az
2
H(0,0,4) =
2[9 + 16] 2
3
a z = 0.36a z A/m
H(0,0, -4) = H(0,0,4) = 0.36a z A/m
olarak bulunur.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
8
Elektromanyetik Teori Bahar 2005-2006 Dönemi
H
H
I
Şekil 6. İçinden akım geçen halka şeklinde bir tel ve tel etrafında oluşan manyetik alan
çizgileri.
Örnek:
Şekilde verilen kare biçimli bir kabloya 1 A akım uygulanmaktadır. Kare şeklin bir
kenarı 1 m olduğuna göre karenin merkezindeki H ve B vektörlerini hesaplayınız?
−7
( μ 0 = 4π × 10 H/m)
Çözüm:
y
I
L/2
5
6
4
7
O
-L/2
L/2
R
3
2
1
-L/2
x
8
A
dx
Şekil 7. Kare biçimli kabloya 1 Amper akım uygulanmaktadır.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
9
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Biot-Savart yasasını tekrar yazıp problemi çözmeye başlayalım. Şekil 7 deki A ve O
noktalarının koordinatları sırasıyla A(x,-L/2,0) ve O(0,0,0) dır.
dH =
Idl × a R Idl × R
=
4πR 2
4πR 3
( )
R = (0 − x)a x + (0 − (− L / 2) )a y + (0 − 0)a z = − xa x + L a y
2
2
R = x2 + L
2
dl = dxa x
( )
R ve dl ifadeleri Biot-Savart yasasında yerine yazılırsa
ax
( )
ay
az
− xa x + L a y = dx
0
2
−x L
2
L
0 = dx a z
2
0
(
( ) )
(( ) )
( ( ))
L
I L dxa z
Idl × R (Idxa x ) × − xa x + 2 a y
2
=
=
dH =
3
3
2
2
2
4πR
4π x 2 + L
4π x 2 + L
2
2
( ( ))
3
2
elde edilir. Şekil 7 den anlaşılacağı üzere problem simetrik olduğu için sadece, karenin
(1) nolu parçasını alıp 8 ile çarpmamız yeterli olacaktır. Son bağıntıdan
(
I (L )dxa )
2
H =8∫
4π (x + (L ) )
2
L
2
z
0
2
2
3
2
integrali yazılabilir. Bu integrali alıp verilenleri yerine yazalım. Bundan önce bu integrali
alabilmek için bu ifadeye daha yakından bakalım. H integral ifadesi
A=∫
(a
dx
2
+ x2 ) 2
3
şeklindedir. Bu ifadenin integralini alalım.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
10
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Hatırlatma: y = tan( x) ise y ′ = 1 + tan ( x) =
2
1
= sec 2 ( x) tir.
2
cos ( x)
x için
x = a tan(t )
i seçelim ve türevini alalım
dx =
adt
cos 2 (t )
1
ve işlemlere devam edelim ve cos( x) =
olduğunu hatırlayalım. Bu
1 + tan 2 ( x)
durumda A integrali
A=∫
(a
1
2
+ a 2 tan 2 (t ) ) 2
3
adt
a cos 3 (t )
1
1
dt = 2 ∫ cos(t )dt = 2 sin t + C
=
2
3 ∫
2
cos (t ) a cos (t )
a
a
olur. Belirsiz integral olduğu için C sabitini sonuca ilave edilmelidir.
tan( x)
sin( x) =
ifadesi hatırlanırsa
1 + tan ( x)
2
( )
x
1
1
tan(t )
1
a
A = 2 sin(t ) + C = 2
+C = 2
2
a
a 1 + tan (t )
a 1 + x2
( a)
A=
1
a2
x
a + x2
2
+C =
2
1 x
1
2
a a 1 + x2
( a)
+C
olarak bulunur. Şimdi bu sonucu biz problemi çözmek için kullanabiliriz.
Dolayısıyla
(
I (L )dxa )
2
H =8∫
4π (x + (L ) )
2
L
2
0
z
2
2
3
2
=
( 2 )a
8I L
4π
L
z
2
∫
0
dx
( ( 2) )
x + L
2
2
3
2
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
11
2
+C
Elektromanyetik Teori Bahar 2005-2006 Dönemi
L
2
∫
0
dx
(x + (L 2) )
2
2
3
integrali dikkat edilirse A ile aynıdır. Bu durumda A nın sonucunu
2
kullanabiliriz.
Böylece a=L/2 dersek
L
L
2
∫
0
dx
1
=
L
2
x
( ( 2) ) ( ) (L 2) + x
x + L
2
2
3
2
2
2
2
0
2
(L 2 ) − 1
0
( ) (L 2 ) + (L 2 ) (L 2 ) (L 2 ) + 0
1
=
L
2
L )
(
1
0
2
2
=
−
=
(L 2 ) (L 2 ) + (L 2 ) (L 2 ) (L 2 ) + 0 L
2
2
1
2
H=
2
( 2)
8I L
4π
4
L2 2
2
2
=
2
1
2
2L
4
=
2
L
2
2
1
2
2L
4
=
2
2 2
4
= 2
LL 2 L 2
4 IL
4 2 IL 2 2 I
=
=
a
πL z
πL2 2 πL2 2
olarak bulunur. Verilenleri denklemde yerine yazılırsa
H=
2 2 .1 2 2
A/m
=
π .1
π
B = μ0 H
B = μ 0 H = 4π × 10 −7
2 2
π
= 8 2 × 10 −7 T (Tesla =
Weber
)
m2
Dünyanın manyetik alanı kutuplarda yaklaşık olarak 6 × 10 T = 6 × 10 nT
−5
4
9
ekvatorda 3 × 10 T = 3 × 10 nT değerindedir 1T = 10 nT ( nanoTesla ) .
−5
(
4
)
ve
Amper yasası- Maxwell Denklemi
Amper yasası elektrostatikte öğrendiğimiz Gauss yasasına benzerdir. Gauss yasasına göre
eğer problem simetri gösteriyorsa elektrik alan kolayca hesap edilebiliyordu. Amper
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
12
Elektromanyetik Teori Bahar 2005-2006 Dönemi
yasasına göre de eğer akım dağılımı simetri özelliği gösteriyorsa manyetik alan kolayca
hesap edilebilir.
Amper yasasına göre herhangi bir kapalı çizgisel yol üzerinde alınan manyetik alanın
integrali bu telde bulunan akıma eşittir. Matematiksel olarak
∫ H ⋅ dl = I
kapalı
(14)
Amper yasasına Stokes teoremini uygulayalım
I kapalı = ∫ H ⋅ dl = ∫ (∇ × H ) ⋅ dS (15)
L
S
yazılabilir. Ayrıca akımın
I kapalı = ∫ J ⋅ dS (16)
S
e eşit olduğu bilindiğinden (15) ve (16) nın sonucu olarak
∇ × H = J (17)
bulunur. (17) ifadesi Maxwell denklemlerinden şu ana kadar öğrendiklerimizden
üçüncüsüdür.
Şimdi Amper yasasını uygulayarak daha önce Biot-Savart yasasıyla çözdüğümüz
probleme tekrar bakalım.
z
Amper yolu
O
P
ρ
y
dl
x
Şekil 8. Amper yasasının uygulanışı.
I kapalı = ∫ H ⋅ dl
L
H ve dl bileşenleri yerine yazılırsa
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
13
Elektromanyetik Teori Bahar 2005-2006 Dönemi
2π
I = ∫ H φ a φ ⋅ ρdφa φ = H φ 2πρ
φ =0
Hφ =
I
2πρ
I
H=
aφ
2πρ
şeklinde bulunur. Beklenildiği gibi problem hem Biot-Savart hem de Amper yasası
uygulanarak çözülebilir.
Manyetik Akı yoğunluğu- Maxwell Denklemi
Manyetik akı yoğunluğu B vektörü ile manyetik alan şiddeti H vektörü arasında, elektrik
alandaki E ve D vektörleri arasındakine benzer ilişki vardır. Bu ilişki
B = μ 0 H (18)
μ 0 boşluğun manyetik geçirgenliği olup, birimi henrys/m veya
−7
kısaca H/m dir. Boşluk için μ 0 nin değeri 4π × 10 H/m dir. Daha kesin bir tanımlama
şeklindedir. Burada
B vektörü için kapalı bir yüzeydeki toplam akı
ψ = ∫ B ⋅ dS (19)
S
ile verilir. Burada ψ manyetik akının birimi webers (Wb) dir. B manyetik akı yoğunluğu
2
2
ise Wb / m dir. B için Wb / m yerine tesla kullanılır. Sonuç olarak bu derste B için
tesla, H için A/m birimlerini kullanacağız.
Elektrik alan için akı formülünü hatırlayalım
ψ = ∫ D ⋅ dS = Q idi. Bu bağıntıya göre
S
toplam akı bu kapalı yüzeydeki yüklerin toplamına eşittir. Bir başka ifadeyle, yükler tek
başına pozitif veya negatif olarak bu kapalı yüzeyin çevrelediği hacim içinde bulunabilir.
Manyetik alan için bu durum söz konusu değildir. Manyetik alanda (19) integraline göre
kapalı bir alanda kuzey veya güney şeklinde ayrı ayrı bulunamazlar. Her koşulda
mıknatısın iki kutbu mevcuttur. Dolayısıyla (19) ifadesi her zaman sıfıra eşittir.
∫ B ⋅ dS = 0 (20)
Manyetik tek kutbun olamayacağı Şekil 8. de verilmiştir. Elinize aldığımız bir çubuk
mıknatısı istediğiniz kadar küçük parçalara bölerseniz bölün yine de en küçük parçanın
iki kutbu olacaktır.
(20) bağıntısına diverjans teoremi uygulanırsa sonuç olarak dördüncü Maxwell
denklemini
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
14
Elektromanyetik Teori Bahar 2005-2006 Dönemi
∫ B ⋅ dS = ∫ ∇ ⋅ Bdv = 0
S
V
∇ ⋅ B = 0 (21)
elde ederiz.
N
N
S
N
S
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
Şekil 9. Küçük bir çubuk mıknatısın parçalara ayrılması. Soldan sağa doğru mıknatıs
parçalara ayrılmasına karşın her parçanın yine iki kutbu vardır. Tek olarak kuzey veya
güney kutup mevcut değildir.
Statik Elektromanyetik alanlar için Maxwell Denklemleri
Buraya kadar statik elektromanyetik alanlar için Maxwell denklemlerini inceledik. Şimdi
Maxwell denklemlerinin hepsini tekrar edelim. Tablo 1 bu zamana kadar incelediğimiz
denklemleri özetlemektedir.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
15
Elektromanyetik Teori Bahar 2005-2006 Dönemi
Statik Elektromanyetik Alanlar için Maxwell Denklemleri
Türev biçimi
∇ ⋅ D = ρv
İntegral biçimi
İsmi
∫ D ⋅ dS = ∫ ρ dv
Gauss yasası
∫ B ⋅ dS = 0
Tek manyetik kutup
yoktur
v
S
∇⋅B=0
v
S
∇×E =0
∫ E ⋅ dl = 0
L
∇×H = J
∫ H ⋅ dl = ∫ J ⋅ dS
L
Amper yasası
S
Tablo 1. Statik elektromanyetik alanlar için Maxwell denklemleri.
KAYNAKLAR
Sadiku, M. N. O., 1995, Elements of Electromagnetics, Oxford University Press.
Edminister, J. A., 1995, Electromagnetics, Schaum’s Outlines, McGraw-Hill.
KOÜ, Mühendislik Fakültesi, Jeofizik Mühendisliği Bölümü, İzmit
16