elektrik devre temelleri laboratuarı yönergesi

1
ELEKTRĐK DEVRE TEMELLERĐ LABORATUARI
YÖNERGESĐ
1. Genel Đşleyiş:
Elektrik Devre Temelleri Laboratuarı (EDTLab) dersi 10 adet deney, proje ve
yılsonu sınavından oluşur. Deneyler deney öncesi hazırlık, deney öncesi soru ve
pratik kısımdan oluşur. Deney öncesi hazırlık ORCAD 16.3 öğrenci versiyonu ile
yapılır.
2. Genel Notlandırma:
EDTLab yarıyıl içi sınav notu, 10 deneyden alınan notlar ve 2 deney ağırlığındaki
projenin aritmetik ortalamasıyla, yılsonu notu ise yılsonu sınavıyla belirlenir.
Yılsonu sınavı uygulamalı ve/veya teorik bir sınavdır. Yılsonu başarı notu yarıyıl
içi notunun %60’ı ve yılsonu notunun %40’ının toplanmasıyla elde edilir. Harfsel
başarı notu hesaplanırken yılsonu başarı notu 20’den daha düşük olanlar çan
eğrisine katılmaz.
3. Deneylerin, Projenin ve Yıl Sonu Sınavının Notlandırılması:
a. Yarıyıl içi deneyleri deney öncesi hazırlık raporu, deney öncesi sorularu ve
uygulama kısımlarından oluşur. Deney öncesi hazırlık raporu grup tarafından
ortak olarak yapılır ve teslim edilir. Deney öncesi hazırlık raporu ve deney
öncesi sorularının deney notuna katkısı %40 tır. Bu not deney raporu notu
çarpı deney öncesi soru notu bölü 100 şeklinde hesaplanır. Örnek olarak grup
deney öncesi raporundan 90 alsın, gruptaki öğrenciler ise a=70, b=90 ve c=100
alsın, deney öncesi notları şu şekilde hesaplanır
d .ö.s.n. 40
d .ö.n = r.n.
x
100 100
70 40
a : 90
x
= 25
100 100
90 40
b : 90
x
= 32
100 100
100 40
c : 90
x
= 36
100 100
d.ö.n. : Deney öncesi notu
r.n.
: Deney öncesi rapor notu
d.ö.s.n.: Deney öncesi soru notu
Deney öncesi hazırlık raporunu teslim etmeyen grup deneye alınmaz. Deneyin
pratik kısmının deney notuna katkısı %60 tir.
b. Her grup bir proje hazırlayacaktır. Projeler simülasyon ve rapor şeklinde
hazırlanacaktır. Yıl içi notuna 2 deney ağırlığında katkı yapacaktır.
c. Yılsonu sınavında deney konularıyla ilgili, biri pratik biri de teorik olmak
üzere iki soru sorulacaktır. Öğrenci bu soruları tek başına cevaplandıracaktır.
4. Devam Zorunluluğu ve Telafi:
EDTLab dersinde devam zorunluluğu %80’dir. On deneyden en az sekizine
katılmayan öğrenciler F0 ile devamsızlıktan kalırlar.
2
5. Grupların Oluşturulması:
Öğrenciler kendi grup arkadaşlarını seçebilirler. Đlan edilen tarihe kadar ilgili
öğretim üye ve yardımcılarına isim yazdıran öğrenciler kendi gruplarını
belirleyebilir. Grup arkadaşı belirtmeyen öğrenciler, ilgili tarihi takip eden gün
içerisinde öğretim üye ve yardımcıları tarafından rastgele eşleştirilirler. Deneyler
başladıktan sonra grupların değiştirilmesi söz konusu değildir. 3. deneyden sonra
deneydeki performanslara göre yeni deney grupları oluşturulacaktır.
6. Bireysel Sorumluluklar:
a. Her öğrenci kendi deney malzemesini bulundurmakla yükümlüdür. Grup
arkadaşı gelmeyen ya da deney sırasında kullandığı malzeme arızalanan
öğrencilerin mağdur olmaması için bu kurala mutlaka uyulması gerekmektedir.
Malzemesi eksik olduğu için deneyini tamamlayamayan öğrenci o deney için
yoklama şartını sağlamış sayılır ancak performans notu 0 (sıfır) olur.
b. Ders programında gruplar arasında hiç boşluk bırakılmadığından, bir grup
deneyini zamanında bitirmediğinde bir sonraki grubun başlaması gecikmekte,
bu da haksızlığa yol açmaktadır. Bu nedenle deneylerin saat başlarından 10
dakika önce tamamlanması gerekmektedir. Yani, bir deney oturumunun süresi
120 dakika değil, 110 dakikadır. Deneyini zamanında tamamlamayan
öğrenciler sözlü soru hakkını ve buna bağlı olarak buradan alacakları 20 puanı
kaybetmiş sayılırlar.
7. Laboratuarda Uyulması Gereken Kurallar:
a. Laboratuar alanına yiyecek, içecek ve sigarayla girmek kesinlikle yasak ve
dersten ihraç sebebidir. Ağzı sıkıca kapatılabilen pet şişelerdeki sular,
içilmediği süre boyunca kapalı kalmak şartıyla bu kuralın dışındadır.
b. Her grup kendine ayrılmış olan araç ve gereci kullanacak; kendine ayrılmış
olan alanda çalışacaktır. Deneye başlamadan önce yapılması gereken ilk iş araç
gerecin çalışır durumda olup olmadığını kontrol etmektir. Grubunuza ayrılmış
araçlardan arızalı olan varsa bunu deneye başlamadan ÖNCE mutlaka
araştırma görevlilerine haber veriniz.
c. Deney boyunca etrafı rahatsız edecek şekilde yüksek sesle konuşmak,
şakalaşmak, başka grupların çalışmalarını engellemek, izin almadan laboratuarı
terk etmek, diğer gruplardan yardım almaya çalışmak ve laboratuarda
dolaşmak laboratuardan ihraç sebebidir.
d. Deney sırasında yapacağınız tüm ölçüm ve çizimlerde kullandığınız birimleri
MUTLAKA yazın. Çizim ve tablolarınızın mümkün olduğu kadar özenli ve
ölçekli olmasına dikkat edin. Ölçekli çizmenize yardımcı olması için
milimetrik kağıt kullanmak iyi bir çözümdür.
e. Araştırma görevlilerinin bilgi ve denetimleri dışında herhangi bir nedenle hasar
verdiğiniz tüm araç gerecin onarım ya da yerine konma bedeli tarafınızdan
karşılanacaktır. Bu nedenle, özellikle (a) şıkkında belirtilen yiyecek-içecek
kuralına özen gösterin.
f. Laboratuarı terk ederken arkanızda boş şişe, kağıt vs. gibi çöpler bırakmayın.
g. Kullandığınız araç gereci işiniz bittiğinde ait oldukları yere ve aldığınız sırayla
yerleştirin.
3
Elektrik Devre Temelleri Laboratuarı dersindeki deneylerde kullanılacak malzemelerin bir
kısmı öğrenciler tarafından sağlanacaktır. Bu nedenle her deney grubunun aşağıda verilen
listedeki malzemeleri alması gerekmektedir.
ELEKTRĐK DEVRE TEMELLERĐ LABORATUVARI
MALZEME LĐSTESĐ
• Aşağıda verilmiş olan E-12 standardındaki direnç değerleri için: 1, 10, 100, 1000, 104
katlarındaki elemanlarından 4’er tane alınacaktır (1/4 Watt).
10 12 15 18 22 27 33 39 47 56 68 82 (Ω
Ω)
• Aşağıda verilmiş olan E-6 standardındaki kapasite değerleri için: 10-11 , 10-10 , 10-9 (nF),
10-8, 10-7, 10-6 (µF), 10-5 katlarındaki elemanlarından 2’şer tane alınacaktır (16 Volt).
10 15 22 33 47 68 (F)
•
Đki adet 1 mH değerinde endüktans (bobin) (Satın aldığınız bobinin 1mH olduğundan
emin olun.)
• Üç adet LM 741 OpAmp tümdevresi
• Penset, yan keski
• 2 m tek damarlı 0.5 mm’lik montaj kablosu
• Multimetre
Not: Bu malzemeler daha sonra Elektronik laboratuarı 1 ve 2 derslerinde de kullanılacaktır.
4
DENEYLERDE DĐKKAT EDĐLMESĐ GEREKEN KONULAR
Deneye ilişkin devrelerin hatasız çalışmasına katkıda bulunmak için dikkat edilmesi gereken
konular aşağıda sıralanmıştır. Bu konulara dikkat edilmesinin bedeli hatayı saptayıp
düzeltmek için harcanan süredir.
•
Deney tablalarının alt ve üstlerindeki yatay bağlantıları besleme ve toprak için
kullanırsanız, devreyi kontrol etmeniz kolaylaşır.
•
Bağlantı tellerinin uçlarındaki plastiği çok fazla sıyırmamalı. Aksi takdirde yan yana
gelen tellerin uçları kısa devre olabilir.
•
Bağlantı tellerini yuvalarına sokarken sıkı geçmeyi sağlamanız yeter. Fazla bastırılması
telin ucunun katlanmasına, sonraki kullanımlarda ise kırılmasına neden olur.
•
Bağlantı tellerini keskin bükmeyiniz, içten kırılıp devrenin normal çalışmasına engel
olabilir.
•
Bağlantı tellerinin uçlarının bükük değil, dosdoğru olmasına dikkat ediniz. Yuvalara
sokma çıkarma işlemi kolaylaşır ve deney setinin ömrü uzar.
•
Bütün yukarıdakileri yapmanıza rağmen beklenen sonuçlar gözlenemiyorsa, kontrolü
aşağıdaki sırada yapmalısınız.
. Yanlış bağlantı
. Kopuk tel
. Elemanların bozuk olması
. Deney seti cihazlarının hatalı olması
. Ölçü aletinin hatalı olması (sigortası atık veya pili bitmiş)
. Osiloskop cihazının hatalı olması
Đlk iki sorun size bağlı olup öncelikle kontrol edilmelidir.
5
Analog ve Dijital Elektronik Eğitim Sisteminin Tanıtımı
Deneyler sırasında kullanılacak laboatuar cihazlarının Đncelenmesi, deneylerin daha verimli
ve faydalı olmasını sağlayacaktır. Bunun için önce laboratuar cihazlarına ait bilgiler, ders
kitabından, ders notlarından ve katalog bilgisi bulunarak incelenmelidir.
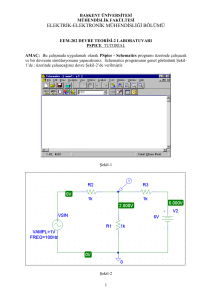
Elektronik devre analizi programının (Electronics Workbench), kullanılması, benzetim
özellikleri incelenecektir. Başlangıç olarak programda bulunan DC gerilim kaynakları, lojik
devre analizinde ve tasarımında kullanılan dijital ölçü aletleri değişik değerler verilerek
çalıştırılacak ve sonuçlar incelenmelidir.
Eğitim Sistemi
Analog ve Dijital Elektronik Eğitim Sistemi, içinde deney tablası, güç kaynakları,
dijital voltmetre, işaret üreteci, darbe üreteci, bas-bırak anahtarlar (butonlar / debounced
pushbuttons), anahtarlar, ayarlı dirençler (potansiyometreler), hoparlör, bnc bağlantısı, 7parça LED göstergeler, lojik 0/1 için LED gösterge birimleri bulunan tümleşik bir sistemdir.
Bu eğitim sistemi lojik devre uygulamalarını öğrenmek, incelemek ve tasarlamak amacıyla
kullanılacaktır. Tümleşik eğitim sistemi, devre ve bağlantılarıyla birlikte Şekil-1’de görülen
biçimdedir.
Şekil 1 Analog ve Dijital Eğitim Sistemi’nin görünümü
Eğitim Sistemi Deney Tablası
Eğitim sisteminde Şekil-1’de resmi görülen, 100 nokta 50 parçalı normal tek damar
bakır montaj kablosu kullanılarak devre elemanları arasında bağlantı yapılabilen bir deney
tablası bulunmaktadır.
Şekil 2 Eğitim sisteminin Deney Tablası
6
Güç Kaynakları
• Sabit DC çıkışlı +5V @ 1.0A, dalgalanma <5mV.
• +V ayarlanabilir DC O/P 0V – 15V arası(150 mA @ 1.3V, 500mA @ +15V maks.),
dalgalanma <5mV
• -V ayarlanabilir DC O/P 0V – -15V arası(150 mA @ -1.3V, 500mA @ -15V maks.),
dalgalanma <5mV
• Sabit orta uçlu AC çıkışlı 12.6VAC(orta uçtan 6.3VAC) @ 100mA maks.
Dijital Voltmetre
Otomatik kademeli bir DC dijital voltmetredir. ± (000.0-199.9) mV, ± (0.200-1.999)V,
± (2.00-19.99)V ve ± (20.0-199.9)V aralıklarında 4 kademesi vardır. Girişi ± 300V’a kadar
yüksek gerilimlere karşı korumalıdır.
Đşaret Üreteci
Frekans Aralığı: 0.1Hz’den 1MHz’e kadar 7 kademe.
Çıkış Gerilimi: 0 - ± 10V (20V tepeden tepeye), kısa devre korumalı.
Çıkış Đşareti Dalga Şekilleri: Sinüs dalga, Kare dalga, Üçgen dalga ve TTL darbe.
Sinüs Dalga: maksimum %3 distorsiyonlu(10Hz – 100kHz aralığında).
TTL darbe: maksimum 25 ns yükselme ve düşme zamanı. 10 adet TTL yük sürebilir.
Kare dalga: maksimum 0.5 µ s yükselme ve düşme zamanı.
Düğüm nokta sayıları: Sinüs, kare ve üçgen dalga için 6, TTL darbe için 2 adet.
Darbe Üreteci
1Hz’den 1MHz’e kadar 6 kademesi bulunan anahtarla seçilebilir pozitif kare dalga
kaynağıdır. Bir anahtar vasıtasıyla 2 tip çıkıştan hangisinin alınacağı belirlenebilir: 5V’luk
tepeden tepeye gerilim veren TTL darbe çıkışı ya da 0V-15V arası tepeden tepeye gerilim
kaynağıyla değeri ayarlanabilir değişken CMOS darbe çıkışı. 8 düğüm noktası ile devrelere
bağlantı yapılabilir.
Bas-Bırak Anahtarlar (Butonlar, debounced pushbuttons)
Her ikisi de OC(open collector) çıkışlı, bir normalde açık ve bir normalde kapalı kontaktan
oluşan ve her biri devrelere bağlantı için 8 düğüm noktasına sahip 2 buton.
Anahtarlar
Lojik Anahtarlar
8 lojik anahtar’ın her biri lojik ‘0’ ya da lojik ‘1’ seviyesini seçmek içindir. Lojik ‘0’ seviyesi
0V iken lojik ‘1’ seviyesi yatay duran 9. anahtar ile deney setinin üzerindeki +5V’luk
kaynağın değeri ya da diğer 0 - +15V arası ayarlanabilir kaynağın değeri seçilebilir.
Düğüm nokta sayısı: her bir anahtar için 2 adet.
SPDT Anahtarlar
2 SPDT anahtar’ın her birinin 2 devreden alınan giriş ve 2 devreye bağlantı yapılabilecek
çıkış olmak üzere 4 düğüm noktası bulunmaktadır. Giriş düğümleriyle anahtarın düşük ve
yüksek seviye için her iki çıkış düğümüne vereceği gerilim değeri belirlenir.
Ayarlı Dirençler (Potansiyometreler)
1 adet 1kΩ ’a kadar ayarlanabilen, 1 adet 10kΩ ’a kadar ayarlanabilen 2 POT’un her birinin 4
adet düğüm noktası bulunmaktadır.
7
Hoparlör
0.25W, 8Ω , 4 adet düğüm noktası.
BNC bağlantısı
Osiloskoptan devreye giriş almak ya da devreden osiloskoba çıkış vermek amacıyla kullanılan
bağlantıdır(BNC kablosu ile yapılır.). 8 giriş/çıkış düğümüne sahiptir.
Göstergeler
Çubuk grafiği(Bar graph):
Giriş gerilim seviyesi 0 - 5V DC olan 10 haneli bir göstergedir. Giriş gerilimi 0V’dan
başlayarak yükseltilmeye başlandığında ilk olarak en soldaki hane yanar, yaklaşık 0.5V
aralıklarla giriş gerilim seviyesi yükseldikçe soldan sağa doğru diğer haneler de yanmaya
başlar.
Đkili kodlanmış onluk girişli 7 haneli gösterge(BCD to seven segment display):
2 adet vardır. Her biri A,B,C ve D giriş düğümlerinden gelecek ikili değerlerden 0-9 arasını
gösterebilirler. 9’dan büyük değerlerde bütün haneler sönük durumda olacaktır. Hiçbir giriş
bağlı değil ise göstergelerden her biri 0 değerini gösterir.
Lojik LED Göstergeler
Lojik ‘1’ seviyesini gösteren 8 kırmızı LED ile lojik ‘0’ seviyesini gösteren 8 yeşil LED.
Lojik ‘1’ eşiği: 2.2V
Lojik ‘0’ eşiği: 0.8V
Giriş empedansı: 100kΩ
Düğüm nokta sayıları: her biri için 2 tane.
8
DENEY NO: 1
DĐRENÇ ELEMANLARI, 1-KAPILI DĐRENÇ DEVRELERĐ VE
KIRCHHOFF’UN GERĐLĐMLER YASASI
Deneyin Amacı:
Direnç elemanlarını tanımak, board üzerinde devre kurma alışkanlığını kazanmak, ohmmetre
ile direnç ölçmeyi öğrenmek, 1-kapılı çeşitli lineer direnç devrelerinin eşdeğerini bulmak,
voltmetre ile gerilim ölçmeyi öğrenmek ve Kirchhoff’un gerilimler yasasını sağlamaktır.
.
Genel Bilgiler:
Direnç Elemanları;
v(t)=Ri(t) ya da i(t)=Gv(t) bağıntısı ile tanımlanan 2-uçlu elemana lineer zamanla değişmeyen
direnç elemanı denir /1/. Şekil 1'de direnç elemanının sembolü ve i-v karakteristiği verilmiştir.
Yukarıdaki tanım bağıntılarında R reel katsayısı direnç elemanının direnci (rezistansı), G reel
katsayısı da iletkenliği (kondüktansı)’dir. Üniversal birim sisteminde R' nin birimi ohm (Ω),
G'nin birimi ise mho (Ω−1) veya siemens (S) dir. Direnç ile iletkenlik arasında GR=1
bağıntısı vardır.
Direnç
elemanının
bağıntısıyla hesaplanır.
ani
gücü p(t)
= v(t)i(t)
=
v(t)
R
2
= i(t)
2
R
Dirençler, elektrik veya elektronik devrelerinde akımı kontrol etmek amacıyla oldukça yaygın
olarak kullanılan elemanlardır.
Dirençler, kullanılacak yere ve amaca göre çeşitli şekillerde üretilirler. Bunlardan başlıcaları:
a) Sabit dirençler
b) Değişken dirençler
c) Foto rezistif dirençler
d) Isıya duyarlı
dirençler
e) Tümleşik dirençler
a) Sabit Dirençler: Fiziksel olarak bir bozulmaya uğramadığı sürece direnç değeri
(rezistansı) değişmeyen yani aynı kalan dirençlerdir. Bunların boyutu ve yapılışı içinden
geçen akıma dolayısıyla üzerinde harcanan güce göre değişir. Düşük güçlerde karbon veya
metal dirençler, yüksek güçlerde ise tel sargılı dirençler kullanılır. Karbon dirençler üretici
firmalar tarafından 1/8 W, 1/4 W, 1/2 W, 1W'lık güçlerde, tel dirençler ise 8 W, 10W, 16 W,
25 W, 40 W, 60W’ lık güçlerde standart olarak üretilirler. Pratik olarak devre
gerçekleştirmelerinde devrede kullanılan direnç elemanlarının güçlerinin seçimine “diğer
elemanların güçlerinin seçiminde de olduğu gibi” dikkat etmek gerekir. Örneğin, teorik
hesaplamalar sonucunda bir devredeki direnç elemanı üzerinde harcanan güç 0.8W olarak
bulunmuş olsun. Pratik olarak tasarlanan devre gerçekleştirildiğinde bu direnç elemanının
gücünü 0.8 W'tan daha büyük olacak biçimde; örneğin standart değerler içinden 1W, seçmek
9
gerekir. Aksi taktirde direnç elemanı üzerinde harcanan aktif güç, direnç elemanının aşırı
ısınmasına ve yanarak bozulmasına neden olur. Karbon dirençlerin direnç değerleri için
yaygın olarak kullanılan standartlar E12 ve E24 standartlarıdır /Ek1/. Standart dirençlerin
değerleri genel olarak iki şekilde belirtilir. Birinci olarak, üretici firma tarafından direnç
üzerine direncin değeri (Ω, kΩ, MΩ olarak) ve güçleri (1/8 W, 1/4 W, 1 W olarak) yazılır.
Đkinci olarak, dirençlerin değerleri ve toleransları renk kodu denilen işaretleme ile belirtilir.
Bu renk kodları ve anlamları, örnekleriyle birlikte Şekil 2'de verilmiştir.
Renk
Siyah
Kahve
Kırmızı
Turuncu
Sarı
Yeşil
Mavi
Mor
Gri
Beyaz
Altın
Gümüş
1. Band
(1.hane)
0
1
2
3
4
5
6
7
8
9
---
2. Band
(2.hane)
0
1
2
3
4
5
6
7
8
9
--Kahve
1
3. Band
(Çarpan)
x100
x101
x102
x103
x104
x105
x106
x107
x108
x109
x10-1
x10-2
Kırmızı
2
4. Band
(Tolerans)
-%1
%2
--%5
%0.25
%0.1
--%5
%10
Sarı
x104
Gümüş
%10
Yeşil
x105
Altın
%5
120.000Ω
120 KΩ
Sarı
4
Mor
7
4.700.000Ω
4.7 MΩ
Şekil 2: Direnç Renk Kodları ve Örnekler
10
b) Değişken Dirençler: Direnç değeri, 0 Ω ile üretici firma tarafından belirlenmiş bir üst sınır
aralığında değişen dirençlerdir. Örneğin 10 kΩ'luk bir değişken direncin değeri 0-10 kΩ
arasında değiştirilebilir. Değişken dirençler bir devrede direnç değerinin sık sık değişmesi
istendiği zaman kullanılırlar. Değişken dirençler istenen güce göre karbonlu veya tel sargılı
olurlar. Değişken dirençler 270 derecelik daire biçiminde (örneğin trimpotlar ve
potansiyometreler) ve düz bir biçimde (örneğin sürgülü potansiyometreler) üretilirler.
c)Foto Rezistif Dirençler: Bunların isminden de anlaşılacağı gibi direnç değeri, üzerine
düşen ışığın şiddetine göre değişen özel dirençlerdir. Bu tip dirençler endüstriyel
uygulamalarda oldukça yaygın olarak kullanılmaktadır.
d)Isıya Duyarlı Dirençler: Direnci ısıya bağlı olarak değişen nonlineer dirençlerdir (PTC,
NTC).
e)Tümleşik Dirençler: Yarıiletken teknolojisiyle üretilen jonksiyon dirençler ve ince-film
dirençlerdir.
Kirchhoff ve Gerilimler Yasası
Gustav Robert Kirchhoff 1824-1887 yılları arasında yaşamış bir Alman fizikçisidir. Elektrik
devreleriyle ilgili çok tanınmış yasalarından başka, spektroskopu keşfetmesiyle optikte ve
kimyada yeni bir çığır açmıştır.
Kirchhoff’un Gerilimler Yasası: Herhangi bir elektrik devresinde, herhangi bir çevreye giren
gerilimlerin cebirsel toplamı, her t anı için sıfırdır. Her bir gerilim bu cebirsel toplama;
gerilim referans yönü çevre yönüyle aynı ise +, gerilim referans yönü çevre yönüyle ters ise işaretli olarak sokulur.
Gerilim ölçmelerinde voltmetre denilen ölçme aletlerinden yararlanılır. Voltmetreler analog
(ibreli) ve dijital göstergeli olmak üzere farklı şekillerde üretilirler. Günümüzde dijital
göstergeli voltmetreler daha yaygın olarak kullanılmaktadır. Đdeal voltmetrelerin iç dirençleri
sonsuzdur. Bu nedenle bir açık-devre elemanı gibi davranırlar. Đdeal olmayan (pratikte
kullanılan) voltmetrelerin iç dirençleri ise oldukça yüksek mertebelerdedir (100MΩ−1GΩ).
Bu değerler voltmetrenin üretim kalitesine göre değişir ve üretici firma tarafından
voltmetrenin kullanım kılavuzunda belirtilir. Voltmetreler, gerilimi ölçülecek olan elemana
daima paralel olarak bağlanırlar. Akım, gerilim ve direnç ölçebilen çok fonksiyonlu ölçü aleti
olan multimetrenin (AVO-metre) voltmetre olarak kullanılabilmesi için üzerinde bulunan
fonksiyon seçici anahtarı (komütatör) mutlaka gerilim kademesine (otomatik kademeli
olmayanlarda maksimum gerilim kademesine) getirilmelidir. Bir voltmetre için en tehlikeli
durum; düşük gerilim kademesinde, o kademe değerinde belirtilen gerilimden daha yüksek bir
gerilim ölçmektir. Bu durumda ya ölçü aletinin sigortası yanabilir ya da daha kötüsü ölçü aleti
tamamen bozulabilir.
Deney Öncesi Hazırlıklar:
1. Renk kodları yardımı ile direnç değerlerinin nasıl okunduğunu öğreniniz.
2. Ohmmetrelerin (analog veya dijital) çalışma prensiplerini araştırınız.
3. Şekil 3, 4, 5, ve 6’daki 1-kapılı direnç devrelerinin giriş dirençlerini hesaplayınız ve
bulduğunuz sonuçları Tablo 1’e yazınız.
4. Şekil 7’deki devrenin tüm düğüm gerilimlerini düğüm gerilimleri yöntemi ile bulunuz ve
Tablo 2’deki hesap sütununu doldurunuz.
5. Bulduğunuz düğüm gerilimlerinden yararlanarak tüm eleman gerilimlerini Şekil 7’de
verilen gerilim referans yönlerine göre hesaplayınız ve Tablo 3’ün hesap sütununu
doldurunuz.
6. Her bir elemanda harcanan aktif gücü hesaplayınız ve Tablo 3’ü doldurunuz.
7. T:{8,7,3,10,5} ağacı için devrenin grafını çiziniz. Tüm temel çevreleri ve gözleri, kümeler
içindeki eleman numaraları ile belirleyiniz.
11
8. Tüm gözler için Kirchhoff’un gerilimler yasasını sağlayıp,
∑V
i
= 0 olduğunu gösteriniz.
i
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki 2. maddeden sonra istenenleri sırasıyla bulunuz
ve düzenli bir şekilde raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
Malzeme ve Cihaz Listesi:
1. 10 Ω direnç 1 adet
2. 100 Ω direnç 6 adet
3. 180 Ω direnç 2 adet
4. 330 Ω direnç 2 adet
5. 390 Ω direnç 1 adet
6. 470 Ω direnç 1 adet
7. 680 Ω direnç 1 adet
8. 1 kΩ direnç 5 adet
9. 1.2 kΩ direnç 1 adet
10. 2.2 kΩ direnç 3 adet
11. 2.7 kΩ direnç 2 adet
12. 4.7 kΩ direnç 1 adet
13. 10 kΩ direnç 1 adet
14. Dijital multimetre
15. Pens (cımbız), montaj kablosu
16. Deney seti (ACT-1, CADET-I veya CADET-II)
NOT: Tüm karbon dirençler 1/8 veya 1/4 W 'tır.
12
Deney Sırasında Yapılacaklar:
1. Deneyde kullanacağınız dijital multimetreydi ohm kademesine getiriniz. Ommetrenin
doğru çalışıp çalışmadığından anlamak için aşağıdaki işlemleri yapınız. Ohmmetrenin uçları
açık iken göstergenin sol tarafında yanıp sönen “1” sayısının olduğundan ve “Low Batt”
mesajının görünmediğinden emin olunuz. Göstergedeki yanıp sönen “1” sayısı ohmmetrenin o
anda ölçtüğü direncin sonsuz (yani açık devre) olduğunu belirtir. Daha sonra ohmmetrenin
uçlarını birbirine birleştiriniz. Bu durumda göstergede çok küçük değerde bir reel sayı
okunacaktır. Bu reel sayı, ölçü aletinin ve probların toplam iç direncidir.(Prob, multimetreye
bağlanan, sivri uçlu kablodur.) Göstergede bunlardan farklı değerler görünmesi durumunda
ölçü aletiniz bozulmuş veya pili zayıflamış olabilir.
2. Elinizdeki pens ile deneyde kullanacağınız dirençlerin iki ucunu “boyları eşit uzunlukta
olacak biçimde” 90 derecelik bir açı vererek bükünüz. Daha sonra Şekil 3, 4, 5 ve 6'da
görülen devreleri, deney seti üzerinde bulunan board’a düzgün bir biçimde kurunuz. Deney
seti üzerindeki boardların bağlantılarını gösteren şekil, ekler bölümündedir.
3. Kontrol işlemi bittikten sonra 1-kapılı direnç devrelerinin giriş dirençlerini ohmmetre ile
ölçerek bulunuz ve Tablo 1’e yazınız.
13
4. Hesap ve ölçme sonucunda bulduğunuz eşdeğer direnç değerlerini karşılaştırarak her
birine ait mutlak ve bağıl hataları bulunuz ve sonuçları Tablo 1’e yazınız.
Herhangi bir X büyüklüğüne ilişkin mutlak hata ∆X ise :
Mutlak Hata=∆X =[XHesap (gerçek değer) - XÖlçme (hatalı değer)]
%Bağıl Hata X=[∆X/XHesap]x100 eşitlikleriyle bulunur. Bu deney için X=Rab dir.
Tablo 1
Devre
TEK KAPILI DĐRENÇ DEVRELERĐ:
Rab [Ω]
Mutlak
Hesap
Ölçme
Hata [Ω]
Bağıl
Hata %
Şekil 3
Şekil 4
Şekil 5
Şekil 6
5. Şekil 7’deki devreyi, gerilim kaynaklarını devreye bağlamadan düzgün bir biçimde board
üzerine kurunuz. Devrenin doğru kurulup kurulmadığından emin olunuz. Daha sonra
voltmetre ile deney seti üzerinde bulunan gerilim kaynaklarının gerilimlerini, kaynaklar
yüksüz durumda iken (yani gerilim kaynaklarının uçları açık devre iken) şemada belirtilen
değerlere göre ayarlayınız. Ayarlanan bu gerilimlerin, kaynakların devreye bağlanması
durumunda da (yani kaynakların yüklenmesi durumunda) değişmediğinden emin olunuz. Bir
azalma varsa gerilimi dikkatlice artırınız. Bu azalmanın nedeni, ideal olmayan gerilim
kaynaklarından akım çekilmesi durumunda (yüklü durumda) kaynak iç direncinde meydana
gelen gerilim düşümüdür.
6. Voltmetrenin – (toprak) ucunu referans noktasına bağlayarak bütün düğüm gerilimlerini
ölçünüz ve Tablo 2’deki ölçme sütununu doldurunuz. Daha sonra voltmetrenin - ucunu
referans noktasından ayırınız.
7. Bütün eleman gerilimlerini Şekil 7’de verilen referans yönlerinde voltmetre ile ölçünüz ve
Tablo 3’deki ölçme sütununu doldurunuz. Hesap ve ölçme sonucunda bulduğunuz tüm
gerilimleri karşılaştırınız.
8. Yalnızca düğüm gerilimlerine ait mutlak ve bağıl hataları hesaplayınız ve sonuçları
Tablo2’deki sütuna yazınız.
TABLO 2
Düğüm
Hesap [V]
Ölçme [V] Mutlak Hata % Bağıl
Gerilimi
Hata
Vd1
Vd2
Vd3
Vd4
Vd5
Vd6
14
TABLO 3
Hesap
Eleman
V9
V10
R1
R2
R3
R4
R5
R6
R7
R8
V [Volt]
5.00
12.00
P [mW]
Ölçme
V [Volt]
Sorular:
1. Hesaplanan değerler ile ölçülen değerler arasında fark var mıdır? Eğer varsa, bu fark
hangi nedenlerden oluşmaktadır? Kısaca açıklayınız.
2. Şekil 3'teki devrede R2 direncinin sırasıyla açık-devre ve kısa-devre yapılması durumunda
devrenin eşdeğer dirençlerini ve kaynaktan çekilen akımları hesaplayınız. Aynı şekilde
Şekil4’teki devrede R3 direnci, Şekil6’daki devrede 1kΩ’luk direnç için işlemleri
gerçekleştiriniz
3. Şekil 7’deki devre için ölçmüş olduğunuz gerilimleri kullanarak devrenin tüm temel
çevreleri ve gözleri için Kirchhoff’un gerilimler yasasının sağlandığını gösteriniz.
4. Şekil 7’deki devrede Tellegen Teoreminin sağlandığını gösteriniz.
5. Voltmetrenin devreye seri bağlanması durumunda gerek devrenin ve gerekse voltmetrenin
çalışmasında bir bozulma olur mu? Nedenleriyle birlikte kısaca açıklayınız.
6. Şekil 7’deki devrenin d1 düğümü kaynak dönüşümü uygulanarak yok edilebilir mi? Yok
edilebilirse nasıl?
7. Şekil 7’deki devrenin d5 düğümünü kaynak dönüşümünden yararlanarak yok ediniz.
8. Şekil 7’deki devrenin düğüm sayısı nedir? Bu devrenin çözümü için kaç tane bağımsız
akım denklemine ihtiyaç vardır?
9. Şekil 7’deki devrede ek denklem sayısı kaçtır? Bu devreye 1 adet 5-uçlu, 2 adet 3- kapılı,
4 adet bağımlı kaynak ve 3 adet bağımsız akım kaynağı uygun bir biçimde bağlandığında ek
denklem sayısı kaç olur ?
EKLER:
• E-12 ve E-24 Standardı, direnç değerleri tablosu
E-24 10 11 12 13 15 16 18 20 22 24 27 30 33 36 39 43 47 51 56 62 68 75 82 91
12
15
18
22
27
33
39
47
56
68
82
E-12 10
• Deney düzeneği bağlantı şeması
15
DENEY NO: 2
KIRCHHOFF’UN AKIMLAR YASASI
Deneyin Amacı :
Board üzerinde devre kurma alışkanlığını geliştirmek, ampermetre ile akım ölçmesini
öğrenmek ve Kirchhoff’ un akımlar yasasını sağlamaktır.
Genel Bilgiler:
Kirchhoff’un Akımlar Yasası: Herhangi bir devrede, herhangi bir düğüme bağlı uç
akımlarının cebirsel toplamı, her t anı için sıfırdır. Her bir akım, bu cebirsel toplama; akım
referans yönü düğümden dışa doğru ise +, akım referans yönü düğüme doğru ise - işaretli
olarak sokulur. Akım ölçümlerinde ampermetre denilen ölçme aletlerinden yararlanılır.
Ampermetreler analog (ibreli) ve dijital göstergeli olmak üzere farklı şekillerde üretilirler.
Günümüzde dijital göstergeli ampermetreler daha yaygın olarak kullanılmaktadır. Đdeal
ampermetrelerin iç direnci sıfırdır. Bu nedenle bir kısa-devre elemanı gibi davranırlar. Đdeal
olmayan (pratikte kullanılan) ampermetrelerin iç dirençleri ise oldukça düşük mertebelerdedir
(0.01Ω−0.1Ω). Bu değerler ampermetrenin üretim kalitesine göre değişir ve üretici firma
tarafından ampermetrenin kullanım kılavuzunda belirtilir. Ampermetreler, akımı ölçülecek
olan elemana daima seri olarak bağlanırlar. Akım, gerilim ve direnç ölçebilen çok fonksiyonlu
ölçü aleti olan multimetrenin (AVO-metre) ampermetre olarak kullanılabilmesi için üzerinde
bulunan fonksiyon seçici anahtarı (komütatör) mutlaka akım kademesine (otomatik kademeli
olmayanlarda maksimum akım kademesine) getirilmelidir. Bir ampermetre için en tehlikeli
durumlardan birincisi, düşük akım kademesinde o kademe değerinde belirtilen akımdan daha
yüksek değerde bir akım ölçmek, ikincisi ise ampermetreyi devreye paralel bağlamaktır. Her
iki durumda da ölçü aletinin sigortası yanabilir ya da daha kötüsü ölçü aleti tamamen
bozulabilir.
Deney Öncesi Hazırlıklar:
1. Şekil 1’deki devrenin tüm çevre akımlarını çevre akımları yöntemi ile bulunuz ve Tablo
1’deki hesap sütununu doldurunuz.
2. Bulduğunuz çevre akımlarından yararlanarak tüm eleman akımlarını Şekil 1’de verilen
akım referans yönlerine göre hesaplayınız ve Tablo 2’deki hesap sütununu doldurunuz.
3. Her bir elemanda harcanan aktif gücü hesaplayınız ve Tablo 2’yi doldurunuz.
4. T:{5,3,6,8,7} ağacı için devrenin grafını çiziniz. Tüm temel çevreleri ve gözleri kümeler
içindeki eleman numaraları ile belirleyiniz.
5. Devrenin temel çevreleri ve gözleri aynı elemanlardan oluşacak biçimde bir ağaç çiziniz
ve ağacı bir küme ile belirtiniz.
6. Tüm düğümler için Kirchhoff'un akımlar yasasını sağladığını gösteriniz.
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki istenenleri sırasıyla bulunuz ve düzenli bir
şekilde raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
16
R1 = 390 Ω
R2 = 680 Ω
R3 = 470 Ω
R4 = 220 Ω
R5 = 1 kΩ
R6 = 560 Ω
V7 = 12 V
V8 = 12 V
Malzeme ve Cihaz Listesi:
1. 220 Ω direnç 1 adet
2. 390 Ω direnç 1 adet
3. 470 Ω direnç 1 adet
4. 560 Ω direnç 1 adet
5. 680 Ω direnç 1 adet
Şekil 1.
6. 1 kΩ direnç 1 adet
7. Dijital Multimetre
8. Deney seti (ACT-1 veya CADET I-IT)
9. Pens, keski, montaj kablosu
Deney Sırasında Yapılacaklar:
1. Şekil 1’deki devreyi, gerilim kaynaklarını devreye bağlamadan, düzgün bir biçimde board
üzerine kurunuz. Devrenin doğru kurulup kurulmadığından emin olunuz. Daha sonra
voltmetre ile deney seti üzerinde bulunan gerilim kaynaklarının gerilimlerini, kaynaklar
yüksüz durumda iken (yani gerilim kaynaklarının uçları açık devre iken) şemada belirtilen
değerlere göre ayarlayınız. Ayarlanan bu gerilimin, kaynakların devreye bağlanması
durumunda da (yani kaynakların yüklenmesi durumunda) değişmediğinden emin olunuz. Bir
azalma varsa gerilimi dikkatlice artırınız. Bu azalmanın nedeni, ideal olmayan gerilim
kaynaklarından akım çekilmesi durumunda (yüklü durumda) kaynak iç direncinde meydana
gelen gerilim düşümüdür.
2. Ampermetrenin + ve - uçlarını Şekil 1’de verilen çevre akımları referans yönlerine göre
bağlayarak her bir çevre akımını ölçünüz ve Tablo 1’deki ölçme sütununu doldurunuz.
3. Bütün eleman akımlarını verilen referans yönlerine göre ölçünüz ve Tablo 2’deki ölçme
sütununu doldurunuz. Hesap ve ölçme sonucunda bulduğunuz tüm akımları karşılaştırınız.
4. Yalnızca çevre akımlarına ait mutlak ve bağıl hataları hesaplayınız ve sonuçları Tablo
1’deki sütunlara yazınız.
Tablo 1
Hesap
Ölçme
Mutlak Hata Bağıl Hata
ÇEVRE AKIMLARI
[A]
[A]
[A]
%
Đç1
Đç2
Đç3
17
Tablo 2
ELEMAN
HESAP
I [A]
P [mW]
ÖLÇME
I [A]
R1
R2
R3
R4
R5
R6
V7
V8
Sorular:
1. Ölçmüş olduğunuz akımları kullanarak Şekil 1’deki devrenin tüm düğümleri ve temel
kesitlemeleri için Kirchhoff’un akımlar yasasının sağlandığını gösteriniz T:{5,3,6,8,7}.
2. Şekil 1’deki devrede Tellegen Teoreminin sağlandığını gösteriniz.
3. Ampermetrenin devreye paralel bağlanması durumunda gerek devrenin ve gerekse ampermetrenin çalışmasında bir bozulma olur mu? Nedenleriyle birlikte kısaca açıklayınız.
4. Şekil 1’deki devreyi akım kaynaklı bir devreye dönüştürünüz. Bu dönüşüm ne gibi
kolaylıklar sağlar? Kısaca açıklayınız.
5. Şekil 1’deki devrenin temel çevre ve göz sayısı nedir? Bu devrenin çözümü için kaç tane
bağımsız gerilim denklemine ihtiyaç vardır?
6. Şekil 1’deki devrede ek denklem sayısı kaçtır?. Bu devreye 2 adet 3-uçlu, 1 adet 4- kapılı,
4 adet bağımlı kaynak ve 2 adet bağımsız akım kaynağı uygun bir biçimde bağlandığında ek
denklem sayısı kaç olur?
7. Farklı değerlerdeki akım kaynakları birbirleriyle seri olarak bağlanabilir mi? Eğer
bağlanamazsa kısaca nedenlerini açıklayınız.
18
DENEY NO: 3
ÇARPIMSALLIK, TOPLAMSALLIK ve RESĐPROSĐTE (KARŞILILIK)
TEOREMLERĐNĐN ĐNCELENMESĐ
Deneyin Amacı:
Devreler teorisinin önemli teoremlerinden biri olan Çarpımsallık, Toplamsallık ve Resiprosite
teoremlerinin, öğrenci tarafından daha iyi kavranmasını sağlamaktır.
Genel Bilgiler:
Çarpımsallık ve toplamsallık teoremi, devrenin lineerliği ile ilgilidir. Daha açık deyişle, bir
devrede Çarpımsallık ve Toplamsallık teoremlerinin geçerli olduğunu göstermek, o devrenin
lineer olduğunu göstermek demektir.
Çarpımsallık Teoremi: Lineer direnç, endüktans, kapasite, çok-uçlular, çok-kapılılar ile
gerilim ve akım kaynaklarından oluşan bir dinamik devrenin elemanlarının akım ve gerilimine
ilişkin öz çözüm yanıtı, yöz(t)=röz(t) ve zorlanmış çözüm yanıtı da yz(t)=rz(t) ise devreye
ilişkin tam çözüm yanıtı, y(t)=yöz(t)+yz(t) dır. Eğer devredeki bütün kaynaklara ilişkin
fonksiyonlar ve enerji depo eden elemanların başlangıç koşulları α (reel bir sayı) katına
çıkarılırsa, bu durumda devrenin öz çözüm yanıtı, yöz(t)=α röz(t), zorlanmış çözüm yanıtı,
yz(t)=α rz(t) ve tam çözüm yanıtı ise y(t)=α[röz(t)+rz(t)] olarak bulunur. Bu deneyde yalnızca
direnç devreleri ile ilgilenilecektir. Dolayısıyla direnç devrelerinde endüktans ve kapasite gibi
dinamik elemanlar olmadığı için yöz(t)=0 dır. Bu nedenle direnç devrelerinin tam çözümü
zorlanmış çözüme eşittir [y(t)=yz(t)]. Çarpımsallık teoremi direnç devreleri için kısaca şöyle
de söylenebilir: Lineer elemanlardan oluşan bir direnç devresinde tüm kaynakların genlikleri
α katına çıkarılırsa, devredeki bütün çıkışlara ilişkin gerilim ve akımların zorlanmış çözüm
yanıtlarının genlikleri de α katına çıkar.
Toplamsallık Teoremi: Bağımsız kaynak sayısı nk’ya eşit olan bir dinamik devrede tüm
başlangıç koşulları (ilk koşullar) sıfırlandıktan sonra kaynaklardan yalnızca biri, örneğin i.
kaynak devrede bırakılsın ve bunun dışındaki bütün bağımsız kaynaklar sıfırlansın. Bunun
pratikteki anlamı gerilim kaynaklarının devreden çıkartılıp yerlerinin kısa-devre, akım
kaynak-larının ise açık-devre yapılmasıdır. Böylelikle içinde sadece i. kaynağın bulunduğu bir
dinamik devrenin elemanlarının akım ve gerilimlerine ilişkin zorlanmış çözümü yanıtı yzi(t)
ile gösterilirse, devreye tüm bağımsız kaynaklar bağlandığında bulunan zorlanmış çözüm
yanıtı;
nk
yz(t) = Σ yzi (t)
i=1
eşitliği ile bulunur. Bu özelliğe dinamik devrelerin toplamsallık özelliği denir. Toplamsallık
özelliği öz çözümler için de geçerlidir. Dinamik eleman sayısı n olan bir devrede yalnızca i.
başlangıç koşulunun devrede bırakılması diğerlerinin sıfırlanması durumunda bulunan öz
çözüm
yözi(t) ile gösterilirse, devredeki tüm başlangıç koşullarının etkisi göz önüne alındığında
bulunan öz çözüm yanıtı;
n
yöz(t) = Σ yözi(t)
i=1
eşitliği ile bulunur.
19
Sonuç olarak toplamsallık teoremi direnç devreleri için kısaca şöyle de söylenebilir: Lineer
elemanlardan oluşmuş bir devrenin zorlanmış çözümü, devredeki her bir kaynaktan dolayı
ortaya çıkan zorlanmış çözümlerin toplamına eşittir.
Resiprosite Teoremi: Resiprosite teoremine geçmeden önce, bir devrede resiprokluk
özelliğinden ne anlaşıldığının belirtilmesi gerekir. Bunun için, aşağıdaki devreyi gözönüne
alalım.
1
2
+
v1(t)
2-kapılı
1′
2′
(a)
1
2
1
2
+
2-kapılı
1′
i2(t)
2′
(b)
i1(t)
2-kapılı
1′
v2(t)
2′
(c)
Şekil 1
Bu devrenin 2-2’ uçları Şekil 1b’de gösterildiği gibi kısa devre edilip, 1-1’ uçlarına v1(t)
gerilim kaynağı bağlandığında, 2-2’ kısa devresinden geçen akım i2(t)’ye eşit olsun. Eğer 1kapısındaki kaynak Şekil 1c’de gösterildiği gibi, 2-kapısına uygulandığında [v2(t)=v1(t)], kısa
devre edilen 1-kapısındaki akım i2(t)=i1(t) oluyorsa, bu 2-kapılı devre resiproktur denir. Bir 2kapılının resiprokluğunu anlamak için çeşitli ölçme düzenleri vardır. Ancak bu deneyde
yalnızca Şekil 1'deki ölçme düzenine göre 2-kapılı bir devrenin resiprokluğu incelenecektir.
Sonuç olarak Resiprosite teoremi; lineer, iki yönlü ve tek bir bağımsız kaynaktan oluşan bir
devrede uyarının yanıta oranının, uyarı ile yanıtın yer değiştirmesi durumunda da
değişmediğini söyler.
Teorem: Lineer direnç, endüktans, kapasite, karşılıklı-endüktans ve transformatörlerden
oluşan ve bütün ilk koşulları sıfır olan 2-kapılı devreler resiproktur.
Deney Öncesi Hazırlıklar:
1. Şekil 2'deki devrede E-F uçlarını açık-devre yapıp, E ucunu bir kısa-devre elemanı ile
GND’ ye birleştiriniz. ICD kısa devre akımını Tablo 1'de verilen Vk1 kaynak gerilimi
değerlerine göre hesaplayınız ve Tablo 1'in hesap sütununu doldurunuz.
2. Elde ettiğiniz ICD hesap değerlerine bakarak bu devrenin çarpımsallık özelliğini sağlayıp
sağlamadığını belirtiniz.
3. Şekil 2'deki devrede VdA=VdB=+Vk1= +5 V ve VdE=VdF= -Vk2 = -12V için yani devrede
toplam iki kaynak olduğunda ICD kısa-devre akımın hesaplayınız ve sonucu Tablo 2'deki
hesap sütununa yazınız. (NOT: Deney setleri içinde Vk1 ve Vk2 gerilim kaynakları simetrik
gerilim üretecek biçimde seri olarak bağlanmış ve deney seti dışına bu kaynakların uçları -V,
0V (GND) ve +V olacak biçimde çıkarılmıştır. Şekil 2'deki şemada kaynakların deney seti
içinde kalan kısmı kesikli çizgilerle gösterilmiştir.)
4. Devrede tek bir kaynak kalacak biçimde sırasıyla önce E-F uçlarını açık-devre yapıp E
ucunu GND’ ye bir kısa-devre elemanı ile birleştiriniz. Böylelikle sadece Vk1 devrede iken
devrenin ICD1 kısa-devre akımını hesaplayınız. Daha sonra A-B uçlarını açık-devre yapıp B
ucunu bir kısa-devre elemanı ile GND’ ye birleştiriniz. Böylelikle sadece Vk2 devrede iken
ICD2 kısa-devre akımını hesaplayınız. Bulduğunuz sonuçları Tablo 2'nin hesap sütunlarına
yazınız.
5. ICD1 ve ICD2 akımlarının toplamını hesaplayınız {ICD=ICD1+ICD2=?}. Elde ettiğiniz sonucu
4. şıktaki ICD değeri ile karşılaştırıp bu devrenin toplamsallık teoremini sağlayıp
sağlamadığını belirtiniz ve sonucu defterinize yazınız.
20
6. Şekil 2'deki devrede E-F uçlarını açık devre yapıp E ucunu bir kısa-devre elemanı ile
GND’ ye birleştiriniz ve Vk1=5V için IR5 yani IF-GND kısa-devre akımını Şekil 2'de gösterilen
referans yönünde hesaplayınız. Đkinci olarak A-B ve E-F uçlarını açık devre yapıp A ucunu
bir kısa-devre elemanı ile E ucuna bağlayınız (böylelikle Vk1 gerilim kaynağı E ucuna
bağlanmış olur) ve B ucunu bir kısa-devre elemanı ile GND’ ye birleştirerek Şekil 2'de
gösterilen referans yönünde IR1 yani IB-GND kısa-devre akımını hesaplayınız. Sonuçları
defterinize yazınız.
7. IF-GND ve IB-GND akımlarını karşılaştırarak Şekil 2'deki devrenin resiprok olup olmadığını
söyleyiniz.
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki istenenleri sırasıyla bulunuz ve düzenli bir
şekilde raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
Şekil 2
Malzeme ve Cihaz Listesi:
1.
2.
3.
4.
100 Ω direnç 1 adet
120 Ω direnç 1 adet
1 k Ω direnç 2 adet
10k Ω direnç 2 adet
5. Dijital Multimetre
6. Deney Seti (ACT-1 veya CADET I-II )
7. Pens, keski, montaj kablosu
Deney Sırasında Yapılacaklar:
1. Şekil 2'deki devreyi board üzerine kurunuz. Ancak bu devrenin E-F uçlarını açık devre
yaparak Vk2 gerilim kaynağını devreden ayırınız, E ucunu bir kısa-devre elemanı ile GND’ ye
birleştiriniz (Vk2=0V). Daha sonra A ve GND uçları arasına voltmetreyi bağlayarak (yani
multimetreyi voltmetre olarak kullanarak) Vk1 gerilim kaynağının değerini Tablo 1'de verilen
gerilim değerine ayarlayınız. Gerilim ayarlama ve ölçme işlemi bittikten sonra multimetreyi
bağlı bulunduğu yerden çıkarıp Şekil 2'de verilen C-D kısa-devre elemanı yerine ampermetre
bağlayarak (yani multimetreyi ampermetre olarak kullanarak) ICD kısa-devre akımını ölçünüz.
21
Bu işlemi Tablo 1'de verilen tüm Vk1 kaynak gerilimi değerleri için tekrarlayıp Tablo 1'in
ölçme sütununu doldurunuz.
2. Şekil 2’deki devrede görülen gerilim kaynaklarının gerilimlerini voltmetre ile hassas
olarak ölçerek VdA=VdB=+Vk1=+5 V ve VdE=VdF= -Vk2= -12 V gerilim değerlerine
ayarlayınız.
Daha sonra C-D kısa-devre elemanı yerine ampermetre bağlayarak devrede iki kaynak varken
ICD akımını (yani R3 direncinin akımını) verilen referans yönünde ölçünüz. Bulduğunuz
sonucu Tablo 2'nin ilgili ölçme sütununa yazınız.
3. Ampermetreyi devrede aynen bırakınız. Şekil 2'deki devrede yalnızca tek bir kaynak
kalacak biçimde sırasıyla önce devrenin E-F uçlarını açık-devre yapıp, E ucunu GND’ ye bir
kısa-devre elemanı ile birleştiriniz. Böylelikle Vk1 devrede iken devrenin ICD1 kısa-devre
akımını ölçünüz. Daha sonra devrenin A-B uçlarını açık-devre yapıp B ucunu bir kısa-devre
elemanı ile GND’ ye, ayrıca E-F uçlarını da bir kısa-devre elemanı ile birbirine birleştiriniz.
Böylelikle Vk2 devrede iken ICD2 kısa-devre akımını ölçünüz. Bulduğunuz sonuçları Tablo
2'nin ölçme sütunlarına yazınız.
4. Şekil 2'deki devrede E-F uçlarını açık-devre yapıp E ucu ile GND’ ye arasına ampermetre
bağlayınız.Vk1=5V için IR5 yani IFGND kısa-devre akımını Şekil 2'de gösterilen referans
yönünde ölçünüz. Daha sonra ampermetreyi devreden çıkarınız. A-B uçlarını açık devre yapıp
A ucunu bir kısa-devre elemanı ile E ucuna bağlayınız ve B ucunu ampermetre ile GND’ ye
birleştiriniz (böylelikle Vk1 gerilim kaynağı E ucuna bağlanmış ve kaynak ile yanıtın yerleri
değiştirilmiş olur). Şekil 2'de gösterilen referans yönünde IR1 yani IBGND kısa-devre akımını
ölçünüz. Sonuçları defterinize yazınız. IFGND ile IBGND akımlarını karşılaştırınız.
Tablo 1
ÇARPIMSALLIK TEOREMĐ:
VK1 KAYNAK
HESAP ÖLÇME
GERĐLĐMĐ
ICD
ICD
[V]
[mA]
[mA]
1
2
4
Tablo 2
TOPLAMSALLIK TEOREMĐ:
KAYNAK KAYNAK
HESAP
VDA=VK1
VDE=-VK2
[mA]
[V]
[V]
5
0
ICD1 =
0
-12
ICD2 =
ICD1+ ICD2=
5
-12
ICD =
BAĞIL
HATA
%
ÖLÇME
[mA]
ICD1 =
ICD2 =
ICD =
Sorular :
1. Karakteristiği Şekil 3.1’de verilen iki uçlu bir eleman için çarpımsallık ve toplamsallık
özellikleri geçerli midir? Neden ?
2. Şekil 3.2'de verilen 2-kapılı devre resiprok mudur?
22
3. Şekil 4’deki devrede R5 direncinden geçen akımı bulunuz. Devredeki gerilim kaynağının
değeri iki kat artırılırsa R5 direnci üzerindeki akımın değeri ne olur?
i(t)
4
1
v(t)
0.1
1
2
Şekil 3.1
1
2
Đdeal Diyot
1Ω
1Ω
1′
2′
Şekil 3.2
R2
R1
10k
+
V
1k
R3
R4
2.2k
R6
1k
1k
5V
R5
Şekil 4
1k
23
DENEY NO: 4
THÉVENĐN, NORTON, MAKSĐMUM GÜÇ TEOREMĐ ve DEVRE
PARAMETRELERĐ
Deneyin Amacı:
Devre analizinin önemli konularından olan Thévenin, Norton ve Maksimum Güç
Teoremlerinin öğrenci tarafından daha iyi anlaşılmasını sağlamaktır ve 2-kapılı direnç
devrelerine ilişkin kısa-devre parametrelerini, DC şartlarda deneysel yoldan bulmaktır.
Genel Bilgiler:
Devre analizinde, çoğu zaman analizi yapılan devrenin akımının veya geriliminin bulunması
istenir. Đlgilenilen elemanın akımını veya gerilimini bulmak için, Çevre Akımları yöntemi ya
da Düğüm Gerilimleri yöntemi kullanılabilir. Bu yöntemler kullanılınca devredeki tüm akım
ve gerilimler ve bu arada ilgilenilen elemanın akım ve gerilimi de bulunur. Görüldüğü gibi
Çevre Akımları yöntemi ve Düğüm Gerilimleri yöntemi kullanıldığında ilgilenilen elemanın
akım ve gerilimini bulmak için bütün devredeki akım ve gerilimleri bulmak zorunluluğu
ortaya çıkmaktadır. Burada akla şu soru gelmektedir; acaba, devredeki bir elemanın akım ve
gerilimini bulmak için daha kısa bir yol var mıdır? Bu sorunun cevabı, Thévenin ve Norton
eşdeğer devreleri ile verilmektedir. Bu bakımdan Thévenin ve Norton eşdeğer devreleri,
karmaşık devrelerin analizinde büyük kolaylıklar getirmektedir.
Lineer bir NA devresinin (NA devresi, lineer direnç, endüktans, kapasite, lineer çok-uçlular ve
kaynaklardan oluşan devredir.) herhangi başka bir NB devresine, Şekil 1’ de gösterildiği gibi
A ve B uçlarından bağlandığını düşünelim. NA ve NB devreleri yalnızca A ve B uçlarından
birbirine bağlıdır. Daha açık bir deyişle, örneğin, NA devresindeki bir endüktans ile NB
devresindeki bir endüktans arasında magnetik yoldan bir bağ yoktur. Lineer olma koşulunun
yalnızca NA devresi için geçerli olduğunu tekrar belirtelim. A-B uçlarındaki v(t) gerilimi ile
NB devresinin çektiği i(t) akımı, NA devresinin yerine Thévenin veya Norton eşdeğer
devresinin konulmasıyla değişmeyecektir. Karmaşık yapıdaki NA devresinin yerine bir
eşdeğer devre
konulması, söz konusu akım ve gerilimlerin hesabını kolaylaştıracaktır.
NA
A i(t)
+
v(t)
)
B
NB
Şekil 1
Thévenin eşdeğer devresi, Şekil 2b’de olduğu gibi, bir gerilim kaynağı ve bir NA0 2-uçlusu ile
gösterilmektedir. Eşdeğer devredeki νth(t) gerilim kaynağı, Şekil 2a’da gösterilen, ilk koşulsuz
NA devresinin A ve B uçları arasında ölçülen açık-devre gerilimine eşittir. O halde, Thévenin
eşdeğer devresindeki νth(t) gerilim kaynağını, NA devresindeki bütün gerilim ve akım
kaynakları belirlemektedir. Thévenin eşdeğer devresindeki NA0 devresi, NA devresinden, bu
devredeki bütün bağımsız gerilim kaynakları kısa-devre, tüm bağımsız akım kaynakları açıkdevre yapılarak elde edilir.
24
-+
A
v
νth(t)
NA
NA0
vth(t)
A
v
B
B
b)
a)
Şekil 2
Norton eşdeğer devresi Şekil 3b’de olduğu gibi, bir akım kaynağı ve bir NA0 2-uçlusu ile
gösterilmektedir.
A
NA
A
iN(t)
NA0
iN(t)
B
a)
B
b)
Şekil 3
Norton eşdeğer devresindeki iN(t) akım kaynağı, Şekil 3a’da gösterilen A-B kısa devresinden
geçen akıma eşittir. NA0 devresi ise, Thévenin eşdeğer devresinde olduğu gibi, NA devresinden
elde edilir.
NA devresi, lineer direnç ve kaynaklardan oluşuyorsa, NA’ ya karşı düşen Thévenin eşdeğer
devresindeki NA0 devresinde bütün elemanlar direnç olacaktır. NA0 direnç devresinin eşdeğeri
Rth ile gösterilirse, NA devresinin Thévenin ve Norton eşdeğerleri sırasıyla Şekil 4a ve Şekil
4b’deki gibi olacaktır.
Rth
A
A
νth(t)
iN(t)
+
-
Rth
B
B
(a)
(b)
Şekil 4
25
Devre Parametreleri Hakkında Genel Bilgiler:
Lineer bir çok-kapılının kapı akım ve gerilimleri arasındaki bağıntılarla tanımlanabilmesi için
kapı sayısı kadar lineer denklem gerekmektedir. En basit çok-kapılı olan 2-kapılı devrelerin
tanımlanabilmesi için de dört değişken cinsinden 2 eşitliğin verilmesi gerekir. Đki değişkenin
diğer ikisince belirlendiği bu eşitlikler 2-kapılıların devre parametrelerini belirler. (Devrede
bağımsız kaynakların olmadığı ve dinamik devrelerin de ilk-koşullarının sıfır olduğu
varsayılmaktadır). Şekil 5'te genel bir 2-kapılı devrenin s-düzlemindeki sembolü verilmiştir.
Şekil 5. Genel bir 2-kapılı devre
2-kapılı devreler çeşitli devre parametreleri ile tanımlanabilir. Bunlardan başlıcaları aşağıda
matrissel olarak verilmiştir.
1. z-parametreleri (açık-devre parametreleri)
 z11
z
 21
z12   I 1 ( s )  V1 ( s) 
=
z 22   I 2 ( s ) V 2 ( s)
2. y-parametreleri (kısa-devre parametreleri)
 y11
y
 21
y12  V1 ( s )   I 1 ( s ) 
=
y 22  V 2 ( s)  I 2 ( s)
3. h-parametreleri (hibrid parametreleri)
 h11 h12   I1 ( s )  V1 ( s ) 
h

=

 21 h22  V2 ( s )  I 2 ( s )
4. g-parametreleri (ters hibrid parametreleri)
 g11 g12  V1 ( s )   I1 ( s ) 
g

=

 21 g 22   I 2 ( s ) V2 ( s )
5. ABCD-parametreleri (zincir parametreleri)
 A B   V 2 ( s )  V1 ( s ) 
C D   − I ( s )  =  I ( s ) 

 2   1 
Bu deneyde incelenen devrelerin, ölçme yolu ile y-parametreleri bulunacak ve doğrudan
devrenin analizinden yararlanılarak, hesap yolu ile bulunan değerlerle karşılaştırılacaktır. Bu
nedenle, aşağıda sadece y-parametrelerinin nasıl bulunacağı açıklanmıştır.
26
y-Parametrelerinin Bulunması:
y-matrisinin elemanları V1 ve V2 gerilimleri sıfır yapılarak yani kapı gerilimleri kısa-devre
edilerek elde edilebilir. Admitans boyutunda olan her bir parametre bu nedenle “kısa-devre
admitans parametreleri” olarak da adlandırılmaktadır.
y11 =
I1 ( s )
I (s)
ve y21 = 2
parametreleri V2(s)=0 olması koşulunda bulunur.
V1 ( s )
V1 ( s )
y12 =
I1 ( s )
I (s)
ve y22 = 2
parametreleri V1(s)=0 olması koşulunda bulunur.
V2 ( s )
V2 ( s )
y11 ve y22 giriş ve çıkış kapılarına ilişkin giriş-admitans fonksiyonlarıdır. y21 “ileri transferadmitansı”, y12 ise “geri transfer-admitansı” olarak adlandırılır.
Devre parametrelerinden yararlanarak bir 2-kapılının iki bağımlı kaynak ve iki empedanstan
oluşmuş devre modelleri kolaylıkla çizilebilir.
Deney Öncesi Hazırlıklar :
1. Şekil 6’da verilen devrede A-B uçlarının solunda kalan 1-kapılı devrenin Gerilim-Akım
(v-i) karakteristiğini çıkarınız.
2. Şekil 6’daki devrenin Thévenin eşdeğer devresini bulunuz..
3. Şekil 6’daki devrenin Norton eşdeğer devresini bulunuz.
4. Bulmuş olduğunuz Thévenin eşdeğer devresinin Gerilim-Akım (v-i) karakteristiğini
çıkarınız ve 1. şıkta Şekil 6’daki devre için bulduğunuz gerilim-akım karakteristiği ile
karşılaştırınız.
5. Şekil 6’daki devrenin Thévenin eşdeğerinden yararlanarak, Rth direncinin 0.1, 1 ve 10 katı
değerindeki RL yük dirençleri için RL ile Rth dirençlerinde harcanan gücü hesaplayınız ve
Tablo 1'in hesap sütunlarını doldurunuz.
6. Şekil 7a, ve 7b’deki devrelerin analizlerini yaparak y-parametrelerini hesap yolu ile
bulunuz ve Tablo 2'deki ilgili sütunları doldurunuz.
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki istenenleri sırasıyla bulunuz ve düzenli bir
şekilde raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
27
R1
A
R3
R2
R4
R5
v(t)
- +
B
Şekil 6.
Şekil 7.
Malzeme ve Cihaz Listesi:
1. 470 Ω direnç 1 adet
2. 1.2 kΩ direnç 1 adet
3. 1.8 kΩ direnç 1 adet
4. 4.7 kΩ direnç 2 adet
7. 10 kΩ direnç 1 adet
8. 33 kΩ direnç 1 adet
7. 47 kΩ direnç 1 adet
8. 1 kΩ direnç 3 adet
9. Dijital Multimetre
10. 7. Deney Seti (ACT-1, CADET I-IT)
11. Pens, keski, montaj kablosu
R1=10 kΩ
R2=1.8 kΩ
R3=1.2 kΩ
R4=33 kΩ
R5=4.7 kΩ
v(t)=10 V
28
Deney Sırasında Yapılacaklar:
1. Şekil 6’daki direnç devresini board üzerine düzgün bir biçimde kurunuz.
2. A-B uçlarındaki açık-devre gerilimini ölçerek, vth(t) gerilimini bulunuz.
3. Devredeki gerilim kaynağını çıkarıp, yerini kısa ediniz. Uçları A ve B olan 2-uçlunun
direncini bir ohmmetre ile ölçerek Rth direncini bulunuz.
4. A-B uçları arasına bir ampermetre bağlayarak (yani ampermetre ile çıkışı kısa-devre
ederek) IN kısa-devre akımını ölçünüz.
5. Bulduğunuz sonuçları Şekil 4 üzerine yazınız. Böylece Şekil 6’da verilen devrenin
Thévenin ve Norton eşdeğer devreleri elde edilmiş olur.
6. Şekil 6’daki devrenin board üzerine Thévenin eşdeğerini kurarak (Rth'nin direnç değeri
için buna en yakın olan standart direnç kullanınız) Tablo 1'deki ölçme sütunlarını doldurunuz.
Bulduğunuz değerlere bakarak devreden RL'ye maksimum güç aktarmak için RL ile Rth
arasında nasıl bir ilişki olması gerektiğini belirtiniz.
Tablo 1
Yük Direnci Hesap Hesap Hesap Hesap Ölçme Ölçme Ölçme Ölçme
IRL
VRL
PRL
PRth
IRL
VRL
PRL
PRth
[mA]
[V] [mW] [mW] [mA]
[V]
[mW] [mW]
RL=0.1Rth
RL=Rth
RL=10Rth
7. Şekil 7a’daki devreyi deney seti üzerinde kurunuz.
8. Deney seti üzerindeki ayarlı gerilim kaynağının gerilimini Vk=+1V’a ayarlayınız.
(Gerilim ölçmelerinde multimetrenin voltmetre konumunda olmasına dikkat ediniz.
Aksi halde ölçü aleti bozulabilir.) Devrenin çıkış kapısını kısa devre ediniz (V2=0V).
Multimetreyi DC ampermetre konumuna getiriniz ve devrenin giriş kapısına, Şekil 1’de
gösterilen akım referans yönünde, seri olarak bağlayınız. Vk gerilim kaynağını giriş kapısına
uygulayınız. (Kaynağı devreye bağladığınızda bu gerilimin değişmediğinden emin olunuz.
Eğer bir değişme varsa; yeniden gerilim kaynağının gerilimini kaynak devreye bağlı durumda
iken, +1V'a ayarlayınız.) I1 akımını ölçerek Tablo 1’i doldurunuz. Daha sonra, ampermetreyi
çıkış kapısındaki kısa devre elemanına, I2 akımı referansı yönünde seri olarak bağlayınız.
(Çıkış kapısındaki kısa devre elemanı kaldırılıp ampermetre ile de çıkış kapısı kısa devre
edilebilir. Ölçme işlemleri için yapılan değişiklikler sırasında Vk gerilim kaynağını devreden
ayırtmayı ihmal etmeyiniz.) I2 akımını ölçerek Tablo2’yi doldurunuz. Giriş kapısına
uygulanan gerilim kaynağı Vk=+1V sabit olduğundan; ölçülen I1 akımı doğrudan y11
parametresine, I2 akımı ise y21 parametresine eşit olur.
9. Devrenin giriş kapısını kısa devre ediniz. (V1=0V) ve Vk gerilim kaynağını devrenin çıkışkapısına uygulayınız. Daha sonra, 3. adımda olduğu gibi sırasıyla giriş ve çıkış kapısındaki
akımları ölçerek Tablo 2’yi doldurunuz. Çıkış kapısına uygulanan gerilim kaynağı, Vk=+1V
sabit olduğundan, ölçülen I1 akımı doğrudan y12 parametresine, I2 akımı ise y22 parametresine
eşit olur.
10. Şekil 7b için yukarıdaki işlemleri tekrarlayınız.
29
Tablo2
V1=1V DC, V2=0V
KOŞULLAR
Deneyde
Đncelenen
Devre
Hesap
y11
[mho]
Hesap
y21
[mho]
V2=1V DC, V1=0V
Ölçme Ölçme
I1 (y11) I2 (y21)
[mA] [mA]
Hesap
y12
[mho]
Hesap
y22
[mho]
Ölçme
I1 (y12)
[mA]
Ölçme
I2 (y22)
[mA]
Şekil 7 a
Şekil 7 b
Sorular:
1. Aşağıdaki şekilde görülen NA devresi, dirençler, sabit gerilim ve akım kaynaklarından
oluşmaktadır. A-B uçlarında 10 Ω’ luk direnç yok iken ölçülen VAB gerilimi 2V olmaktadır.
Bu uçlara 10Ω’ luk direnç bağlandığında VAB gerilimi 1V değerine düşmektedir. Buna göre
NA devresinin Thévenin eşdeğerini ve i-v bağıntısını bulunuz.
+
VC (t)
-
NA
10Ω
B
2. Aşağıdaki devrenin Thévenin ve Norton eşdeğer devrelerini bulunuz.
R
kR
A
+
v(t)
2A
B
3.
4.
5.
6.
Şekil 7’deki devreler resiprok mudur? Neden?
Resiprokluk koşulunu; z, y, h, g ve ABCD devre parametreleri cinsinden tanımlayınız.
Şekil 2’deki devrelerin küçük işaretlerdeki z, y, h ve g devre modellerini çiziniz.
Genel bir 2-kapılı devrenin giriş ve çıkış kapılarına sırasıyla R1 ve R2 dirençleri seri
olarak bağlanmış ve yeni bir 2-kapılı devre elde edilmiştir. Genel 2-kapılı devrenin;
a) NIC (negatif çevirici) olması,
b) Pasif-Jiratör olması,
c) Đdeal-transformatör olması durumunda z, y, h, ve g parametrelerini bulup, her
birine ilişkin devre modellerini çiziniz.
30
DENEY NO:5-6
OSĐLOSKOP KULLANIMI
Deneyin amacı:
Osiloskobu tanımak ve osiloskop yardımıyla bir elektriksel işaretin genlik, periyot ve
frekansını ölçmesini öğrenmektir.
Genel Bilgiler:
Osiloskop, devre elemanlarının karakteristiklerinin çıkartılmasında ve zamana bağlı olarak
değişen gerilimlerin incelenmesinde kullanılan bir ölçü aleti olup, çok hızlı değişen bir veya
birden fazla sinyalin aynı anda incelenmesinde, genlik, frekans ve faz ölçümlerinde kullanılır.
Zamana bağlı olarak değişen bir akım veya gerilim fonksiyonu, ibreli (analog) veya sayısal
(digital) bir ölçme aleti ile ölçülebilmektedir. Fakat bu aletler fonksiyonun gerçek değişimi
hakkında bilgi verememektedirler. Ancak değişim, kısa aralıklarla okunan değerlerin (zamanı
da kaydederek) bir eksen takımı üzerinde gösterilmesi ile görülebilir ise de bu oldukça zor bir
iştir. Bu nedenle, işareti zaman düzleminde gösteren bir ölçüm aleti olan osiloskoplar imal
edilmiştir.
Şekil 1. COS5021 model osiloskobun ön paneli
Prob (Probe): Đncelenecek işaretlerin osiloskop cihazına aktarılması için kullanılan bir çeşit
kablodur. Bir ucu osiloskoba bağlanırken sivri olan diğer ucu devredeki incelenecek işaretin
bulunduğu düğüme temas ettirilerek kullanılır. Probun bu ucunda genellikle krokodil
konnektörü şeklinde bir de toprak bağlantısı bulunur. Osiloskop probları x1 ve x10 şeklinde
ayarlanabilirler:
x1 : izlenen sinyali bozmadan ve değiştirmeden osiloskoba ulaştırır.
x10 : izlenen sinyal onda birine zayıflatılarak osiloskoba ulaştırılır. Bu takdirde, sinyalin
gerçek genlik değeri ekranda görünen değerlerin 10 katıdır.
31
Bir osiloskobun kontrolünü sağlayan düğmeler üç gruba ayrılır;
GÖRÜNTÜ (DISPLAY) GRUBU:
Kalibrasyon(CAL)-(1):Osiloskobun özelliklerini test etmeye yarayan kare dalga osilatörü.
Üzerinde frekansı ve genliği belirtilir. Osiloskobun test edilmek istenen kanalına prob
yardımıyla uygulanır. Toprak bağlantısını yapmaya gerek yoktur.
Güç (Power)-(3): Osiloskop cihazının aç/kapa düğmesi. Cihaz çalışır durumda iken bu
düğmenin üzerindeki LED (2)’de yanar.
Parlaklık (Intensity)-(4): Bu düğme ile ekrandaki çizginin parlaklığı ayarlanır. Kullanıcının
gözlerinin zarar görmemesi ve ekranın (CRT) uzun ömürlü olması için parlaklığın,
görüntünün görülebildiği en düşük ayara getirilmesi gereklidir.
Odaklama (Focus)-(6): Ekrandaki benek veya çizginin, uygun netlikte olmasını sağlar.
Yatay eğim (Trace rotation)-(7): Ekrandaki çizginin yatay eksene olan açısını ayarlar.
Aydınlatma (Illum)-(8): Ekran zemininin aydınlatılmasını sağlar.
Ekran (Screen)-(34): Yatay ve dikey çizgilerle bölünmüş bir koordinat sistemine sahip
osiloskop ekranı. Đncelenen işaretler buradan izlenir.
DÜŞEY KUVVETLENDĐRĐCĐ (VERTICAL AMPLIFIER) GRUBU:
Her bir kanal (CH1 ve CH2) için ayrı olarak birer tane ayar düğmesi mevcuttur.
Genlik (VOLTS/DIV)-(12),(16): Bu düğme ile dikey saptırma çarpanı seçimi yani dikey
eksenin ölçeklendirilmesi yapılır. Bu sayede ekrandaki yatay çizgilerin arasının kaç voltluk
gerilime karşılık düşeceği ayarlanır.
Değişken Ayar (Var)-(13),(17): Bu düğme ile düşey saptırma çarpanı hassas olarak
arttırılarak yüksek genliklere sahip işaretlerin incelenmesi sağlanır. Bu düğme tamamen sağa
çevrilip kilitlenirse Volts/div değeri aynen alınır. Bu düğme tamamen sola çevrilirse Volts/div
değeri 2.5 katsayısı ile çarpılmalıdır.
Giriş Kuplaj Seçici (Input Coupling Selector)-(10),(19): Her kanal için bir tane bulunur.
Düşey kuvvetlendirici girişine uygulanacak işaretin kuplajı seçilir.
AC: Giriş sinyali, düşey kuvvetlendiriciye bir kapasite üzerinden uygulanır. Bu kapasite,
işaretin DC bileşenini bloke eder ve sinyalin sadece AC bileşeninin görüntülenmesini sağlar.
GND: Bu konumda düşey kuvvetlendirici girişi topraklanır. Bu takdirde ekrandaki çizginin
bulunduğu yer toprak (referans, GND) seviyesini gösterir.
DC: Bu konumda düşey kuvvetlendiriciye işaretin tüm bileşenleri uygulanır. Eğer bir işaretin
tüm bileşenleri görülmek isteniyorsa, anahtar bu konumda olmalıdır. Düşük frekanslı işaretler
bu seçenekte incelenmelidir.
Đşaret Girişleri:
Kanal 1[X girişi] (Channel 1)-(11)
Kanal 2[Y girişi] (Channel 2)-(18)
Bir dış sinyalin düşey sapma sistemine uygulandığı iki adet BNC tipi konnektör bulunur.
Giriş direnci 1MΩ değerindedir. Bu girişe uygulanabilecek en yüksek gerilim seviyesi kanal
girişinde yazılıdır (genellikle 400 Volt).
Pozisyon (Position ⋅)-(9),(20): Ekrandaki görüntü düşey olarak hareket ettirilebilir.
Düşey Mod (Vertical Mode)-(14): Kanal 1 ve 2’nin işlem modlarının seçimini sağlar.
CH1: Yalnızca CH1 (X girişi) girişine uygulanan sinyal ekranda görüntülenir. (X-Y modunda
bir çalışma oluyorsa bu mod seçilmelidir.)
CH2: Yalnızca CH2 (Y girişi) girişine uygulanan sinyal ekranda görüntülenir.
ADD: CH1 ve CH2’den uygulanmış iki işaretin toplamını gösterir.
DUAL:Đki kanalı birden izlemeyi sağlar. Bazı osiloskop modellerinde bu mod ikiye
ayrılmıştır:
ALT(alternate): Yüksek frekanslı (T < 1 ms) iki işaretin aynı anda görüntülenmesi için;
CHOP: Düşük frekanslı işaretlerin (T > 1ms ) aynı anda incelenmesi için kullanılır.
32
TARAMA (TIME BASE) GRUBU:
Tetikleme, incelenen işaretin ekranda doğru ve net olarak görülebilmesi için kullanılan bir
işlemdir. Bu işlemin faydasını açıklamak için bir örnek verelim: Dönmekte olan bir tekerleğin
veya pervanenin, hızına bağlı olarak insan gözü onu sanki duruyormuş veya çok yavaş
dönüyormuş gibi görür. Benzer şekilde, incelenen işaretin periyodu osiloskop tarafından
doğru olarak algılanıp, otomatik olarak doğru ayar yapılamazsa, ekrandaki görüntü sanki sağa
veya sola hareket ediyormuş gibi görülecektir. Tetiklemenin doğru olması için işaretin belirli
aralıklar işin periyodik olması gereklidir.
Level (Seviye)-(21): Tetiklemenin arzulanan bir noktadan başlamasını sağlayan bir düğmedir.
EXT girişi (External Trigger)-(23):Bu girişe dışarıdan bir tetikleme sinyali uygulanabilir.
Uygulanabilecek gerilim seviyeleri girişin hemen altında yazılıdır.
Slope (Eğim)-(24):Tetiklemenin pozitif / negatif eğimle yapılmasını sağlayan bir anahtardır.
Kuplaj (Coupling)-(25):Tetikleme kaynağı ile tetikleme devresi arası kuplaj seçilir.
AC: AC kuplaj
HF REF: AC kuplaj türü. 50 kHz’den yüksek frekanslı işaretler kabul edilmez.
DC: DC kuplaj
TV: Televizyon işaretlerinin incelenmesinde kullanılır. Bu amaçla tetikleyici devre,
televizyonun senkronizasyon ayırıcı devresi ile birleştirilir.
Tetikleme Kaynağı (Triggering Source)-(26): Tetikleme kaynağının seçimi yapılır:
CH1: Birinci kanaldan uygulanan sinyali tetikleme sinyali olarak kabul eder.
CH2: Đkinci kanaldan uygulanan sinyali tetikleme sinyali olarak kabul eder.
LINE: Şebeke frekansını tetikleme sinyali olarak kabul eder.
EXT: Dışarıdan (EXT girişi) uygulanan bir sinyali tetikleme sinyali olarak kabul eder.
Kararlı bir görüntü için dış tetikleme sinyali ile ekranda görüntülenmesi istenen sinyal
arasında bir bağıntı olmalıdır.
Tetikleme veya Süpürme modu(Triggering or Sweep Mode)-(28):
AUTO: Ekrandaki görüntüyü 20 Hz’lik bir tetikleme sinyali ile tetikler. Tetikleme seviyesi
level düğmesi ile ayarlanır.
NORM: Ekrandaki görüntüyü tetikleme sinyali olarak kabul eder.
SINGLE: Tekil tarama (süpürme) işleminde kullanılır.
Zaman ayarı (Time/Div)-(30): Bu komütatör ile yatay tarama değerleri seçilerek yatay
eksenin (zaman ekseni) ölçeklendirilmesi yapılır. Ayar değeri periyot ölçümünde kullanılır.
VAR Time/Div-(31): Var düğmesi en sağa çevrilerek kilitlenirse, Time/Div’ deki değer
olduğu gibi alınır. VAR düğmesi açılıp en sola getirilirse, 2.5 kat daha yavaş işaretler de
(daha büyük periyoda sahip işaretler) incelenebilir.
Pozisyon(Position ↔ )-(32):Bu düğme ile ekrandaki görüntü yatay olarak hareket ettirilir.
Osiloskopta, kaybolan görüntünün bulunması:
Bu amaçla ilk olarak parlaklık düğmesinin durumu kontrol edilir. Bu düğme orta konuma
getirilir. Daha sonra hangi kanaldan işaret uygulanmışsa, bu kanalın kuplajı GND konumuna
alınır. Ardından düşey hareketi sağlayan düğme (↨) yardımı ile işaret bulunur. Bulunan çizgi,
ekranın ortasında bulunan yatay ekseni örtecek şekilde konumlandırılır. Bu seviye, toprak
(referans) seviyesine karşı gelmektedir. Daha sonra işaret hangi modda (AC veya DC)
incelenecekse, kuplaj seçici anahtar bu konuma getirilir.
Osiloskopta görülen işaretlerin incelenmesi:
Osiloskop, elektriksel işaretlerin (gerilimlerin) zamanla nasıl değiştiğini incelemek için
kullanılır, Bu nedenle periyot ölçümü önemlidir. Bir işaretin periyodunu ölçmek için, bir tam
dalga boyunun kaç kare (div) genişliğinde olduğuna bakılır. Bu değer Time/div kademesinde
ayarlanan değerle çarpılarak periyod süresi (T) elde edilir.
33
Eğer işaretin frekansı isteniyorsa:
1
f =
T
Formülü ile frekans elde edilir.
Osiloskop ekranında görülen işaretin belli bir andaki genlik değerini elde etmek için dikey
eksen izlenir. Đşaretin o andaki değerinin toprak seviyesine olan uzaklığı ölçülür. Bu elde
edilen değer genlik ayarı ile belirtilen (Volts/div) değerle çarpılır. Örnek:
Şekil 2
Şekil 2’de görülen işaretin genlik ve
frekansını bulmak için şu adımlar
izlenir:
1. Đşaretin bir tam periyodu ölçülür:
T = 7 div (kare)
2. T hesaplanır: (30) Time/div = 0,1 ms
T = 7*div ⇒ T= 0,7 ms =700µs
3. f = 1/T formülünden frekans değeri:
f = 1428 Hz
4. Tepeden tepeye genlik değeri:
G = 3,5 div (kare)
5. A hesaplanır: (12) Volts/div = 1 V
G = 3,5*1V = 3,5 V
A = G/2=1,75 V
6. Sonuç: Vi(t) = A*sin(2πf t)
Vi(t) = 1,75*sin(2π*1428 t)
Osiloskopta, X-Y Çalışma Modu:
Bazen biri diğerinin bir fonksiyonu [y=f(x)] olan iki işaretin değişimi incelenmek istenebilir.
Bu takdirde osiloskopta, X-Y çalışma modu kullanılır. Bu amaçla Time/Div anahtarı X-Y
konumuna alınıp(Bazı osiloskop modellerinde X-Y modu Time/Div dışındaki başka bir
düğme ile ayarlanır), düşey modda hangi kanal X-Y çalışma modu için kullanılıyorsa bu
kanal seçilir. Bu takdirde yatay eksen, zamanı değil, X kanalından girilen işareti temsil eder.
Düşey eksen de yatay eksendeki işaretin fonksiyonu olan diğer bir işareti gösterir. Böylece iki
işaret arasındaki ilişki ekranda görüntülenir.
Örnek verirsek: önce bir fonksiyonu koordinat sisteminde nasıl çizeceğimizi düşünelim.
Bunun için en iyi yol belli x değerleri için y=f(x)’in sonuçlarının hesaplamaktır. Daha sonra
bu değerler X-Y düzlemine noktalar konularak gösterilir ve bu noktalardan geçen eğri çizilir.
Osiloskopta ise sürekli değişen bir işaretin (gerilim) yatay eksene verilmesi üzerine dikey
eksende diğer işaretin aldığı değerler izlenir.
Örneğin, Şekil 3a’daki devreyi inceliyelim. Devredeki iki kapılının çıkış geriliminin
fonksiyonu şu şekildedir:
2
Vo = Vi
Şekil 3a’daki devrede, 2-kapılının girişine
V1(t) = Vi(t) =Sin(2π*1000t) V biçiminde bir
işaret uygulanırsa , giriş Vi(t) ve çıkışın Vo(t)
zamana göre değişimleri Şekil 3b’deki gibi
olur.
Gerekli
osiloskop
bağlantısı
yapıldığında ve DUAL modu ayarlandığında
iki işaret Şekil 3b deki gibi ekranda da
görülür.
Şekil 3a
34
Şekil 3b
Bu durumdayken osiloskop X-Y Moduna alınırsa iki kapılının giriş-çıkış karakteristiği
ekranda görülür. Bu karakteristik de Şekil 3c gösterilmiştir.
Not: Yukarıdaki şekillerde, eksenler üzerinde ölçeklendirme yapılmamış, dikey ve yatay
eksenlerin ölçekleri sol alt köşelerde belirtilmiştir. Her iki kanalın da genlik ayarları aynıdır.
Deney Öncesi Hazırlıklar:
1. Osiloskop düğmelerinin işlevini öğreniniz.
2. Şekil 4b’de verilen devrede VR3 gerilimini v1(t) ve V2 cinsinden elde ediniz. Zamana göre
çiziniz değişimini çiziniz.
3. Tablo 1’deki periyot sütununu hesaplayarak doldurunuz.
4. Şekil 4c’deki devrede R1 >> R5 olması durumunda
Malzeme ve Cihaz Listesi:
1. R1= R2= R3= 2.2kΩ üç adet direnç
2. R4= 4.7kΩ bir adet direnç
3. R5= 82 Ω bir adet direnç
4. Bir adet Milimetrik kağıt
5. Dijital Multimetre
6. Deney Seti (CADET-I ve II)
7. Osiloskop ve iki adet prob
8. Pens, keski, montaj kablosu
CH X
oranını bulunuz.
CH Y
35
Deney Sırasında Yapılacaklar:
Şekil 4
1- Şekil 4a’da gösterilen devreyi kurunuz. Daha sonra aşağıda verilen şekilde v1(t) gerilimini
ayarlayınız. Bu ayarlamayı yaparken osiloskop ekranındaki işaretin periyodundan
faydalanmanız gerektiğini unutmayınız.
• v1(t) = sin(2π*1000t) V
• v1(t) = 2*sin(2π*20000t) V
2- Şekil 4b’deki devreyi kurunuz. v1(t) ve V2 gerilimlerini Tablo 1’e göre ayarlayınız.
Osiloskop ekranında gözlediğiniz işaretleri ölçekli olarak çiziniz. (Not: CH1’in kuplaj
ayarının DC olması gereklidir, nedenini düşününüz)
Tablo 1
Adım
1
2
3
A
1
2
2
v1(t)= A*sin(2πf t) V
F [Hz]
T=1/f [ms]
5 000
10 000
50 000
V2 [Volt]
2
2
5
3- Şekil 4c’deki devreyi kurunuz.v1(t)=4*sin(2π*200t) Volt olarak ayarlayınız.
Osiloskobu DUAL moduna getirerek ekranda gördüğünüz işaretleri ölçekli olarak çiziniz
4- Osiloskobu X-Y moduna getirerek ekranda gördüğünüz şekli çiziniz ve yorumlayınız.
5- Aynı devrede R1 yerine R4 bağlayınız. Osiloskobun X-Y modunda gözlediğiniz işareti
çiziniz.
Sorular:
1- Herhangi bir iki uçlu elemanın akım-gerilim karakteristiği osiloskop yardımıyla nasıl
incelenebilir?
2- Osiloskobun X-Y modunda yatay eksen için ayarlanacak AC kaynağın frekansının
seçiminde nelere dikkat edilmesi gerekir? (Đpucu: Bu frekansın düşük olmasının
yaratabileceği sorunlar nelerdir?)
3- Osiloskobun birinci kanalına v1(t)=sin(2π10.000t) V, ikinci kanalına ise
v2(t)=sgn[sin(2π5.000t)] V biçiminde birer işaret uygulanırsa, DUAL (ALT veya CHOP)
ve ADD modlarında gözlenecek işaretleri ölçekli olarak çiziniz.
: x ≥ 0
+ 1
Not: sgn( x) = 
 (işaret fonksiyonu)
: x < 0
− 1
4- Osiloskobun girişlerine sırası ile v1(t)= sin(2π400t) V ve v2(t)=cos(2π400t) V işaretleri
verildiği taktirde; DUAL (ALT veya CHOP) ve X-Y modlarında gözlenecek işaretleri
ölçekli olarak çiziniz.
36
DENEY NO: 7
RL, RC ve RLC’ DEN OLUŞMUŞ DEVRELERDE GEÇĐCĐ
REJĐMLERĐN ĐNCELENMESĐ
Deneyin Amacı:
Öğrencinin, elektrik devrelerin zaman domeninde incelenmesiyle ilgili bilgilerinin artırılması
amaçlanmaktadır.
Genel Bilgiler:
Bir elektrik devresinin zaman domeninde incelenmesi için, önce o devrenin ya entegrediferansiyel denklemlerinin, ya da durum denklemlerinin yazılması gerekir. Bu denklemlerin
çözülmesiyle devrenin zaman domenindeki incelenmesi tamamlanır. Bilindiği gibi,
diferansiyel denklemlerin çözülmesiyle ortaya çıkan çözümü iki parçaya ayırtmak
mümkündür: Çözümün birinci parçasını devredeki ilk koşullar, ikinci parçasını da devredeki
kaynaklar belirler. Çözümün bu parçalarına, sırasıyla Öz ve Zorlanmış Çözüm adları verilir.
Asimptotik kararlı, diğer bir deyişle t → ∞ için durum geçiş matrisi φ(t)’nin sıfıra uzandığı bir
devrede, t → ∞ giderken öz çözüm sıfıra, zorlanmış çözüm de özel çözüme ulaşır. Daha açık
bir deyişle, asimptotik kararlı bir devrede, devrenin incelenmesine başlanılmasından belirli bir
zaman sonra, tam çözüm büyük bir yaklaşıklıkla özel çözüme eşit olur. Asimptotik kararlı bir
devre için tam çözümü, geçici çözüm ve kalıcı (sürekli) çözüm olarak iki parçadan oluşuyor
diye düşünebiliriz. Asimptotik kararlı bir devre için diferansiyel denklem sisteminin homojen
çözümüne geçici, özel çözümüne de kalıcı çözüm denilmektedir. Geçici çözüm, başlangıçta
çok büyük olsa bile, devre çalışmaya başladıktan belirli bir zaman sonra küçülür, sıfıra
yaklaşır. Kalıcı çözüm, devrede kaynaklar olduğu sürece devam edecek çözümdür. Etkisi çok
kısa sürmesine karşın geçici çözüm bir devrede elemanların seçilmesi bakımından önemlidir.
Örneğin, elektrik enerjisi dağıtım sisteminde (şebekede) sistem çalışırken birdenbire meydana
gelen arızadan (kısa devre gibi) dolayı, arızanın olduğu andan itibaren ortaya çıkan geçici
çözümün şebekedeki hatların, cihazların, ölçü transformatörlerinin ve anahtarların seçimi
bakımından bilinmesi gerekir. Eskiden şebekedeki anahtarların “açma zamanlarının” büyük
olmasından dolayı, arıza halinde ortaya çıkan geçici çözümle açma zamanından kısa sürdüğü
için ilgilenilmezdi. Bugün açma zamanları küçük olduğu için geçici çözümle ilgilenilmesi,
şebekedeki elemanların seçilmesinde göz önüne alınması gerekmektedir. Devrelerin zaman
domeninde incelenmesi, birçok cihazın çalışma ilkelerinin ve işlevlerinin anlaşılması
bakımından çok önemlidir.
Bu aşamada basit birer RC, RL ve RLC devreleri ele alınarak, bunların basamak, darbe ve kare
dalga kaynaklarıyla uyarılması halinde çözümlerinin ne olduğu incelenecektir.
RC Devresi:
Şekil 1’deki RC devresini ele alalım. Bu devrenin durum denklemleri,
R
+
e(t) ∼
+
C
Şekil 1
dvc
1
1
=−
vc +
e(t )
dt
RC
RC
biçimindedir.
(1)
37
(1) denkleminde e(t)=Eu(t) biçiminde basamak fonksiyonu ise, denklemin çözümü;
vC(t) = e -t / RC vC (0) + E(1-e -t / RC )
(2)
olmaktadır. vC(0) = 0 olması halinde, C ve R’nin uçlarındaki gerilimlerin değişim biçimleri
Şekil 2’de gösterildiği gibidir.
vC(t)
vR(t)
E
E
Kapasitenin
dolması
Kapasitenin
boşalması
t
t
Şekil 2
Şekil 1’deki devrede, e(t) kaynağı çıkartılıp yeri kısa devre edilirse ((1) denkleminde e(t) = 0
alınırsa) (1) denkleminin çözümü,
vC(t) = e -t / RC vC(0)
(3)
biçimindedir. Bu gerilimin zamanla değişim biçimi Şekil 3’de gösterilmiştir. (2) ve (3)
denkleminde görülen RC devrenin zaman sabiti olup; R, ohm, C ise farad olarak
konulduğunda birimi saniyedir.
vC(t)
Kapasitenin boşalması
vC(0)
vC(0)/e
t
RC
Şekil 3
Şekil 1’deki devrede e(t) kaynağı, Şekil 4a’da gösterildiği gibi bir darbe kaynağı ise,
(e(t) = E[u(t) - u(t-∆)]), vC(0) = 0 olmak üzere, kapasitenin gerilimi;
vC(t) = E(1- e -t/RC )u(t) - E(1- e -(t-∆)/RC )u(t - ∆)
(4)
olarak ifade edilir. C kapasitesinin ve R direncinin gerilimi Şekil 4b ve Şekil 4c’de
gösterildiği gibidir.
e(t)
vC(t)
vR(t)
E
E
vC(∆)
E - vC (∆)
t
∆
(a)
t
∆
t
∆
(b)
Şekil 4
-vC(∆)
(c)
38
e(t) kaynağının Şekil 4a’daki gibi darbe kaynağı olması halinde, Şekil 1’deki devreyi Şekil
5’deki gibi düşünmek mümkündür.
1
A
R
+
E
2
C
Şekil 5
Bu durumda, Şekil 5’deki A anahtarının ∆ zaman kadar 1 konumunda tutulduğu, sonra 2
konumuna alındığını belirtmek gerekir. A anahtarı 1 konumundayken, 0 ≤ t < ∆ aralığında, C
kapasitesinin uçlarındaki gerilim ifadesi olarak Şekil 4b’deki eğrinin sıfırdan ∆’ya kadar olan
aralıktaki kısmı geçerlidir. t = ∆ olduğunda, kapasitenin gerilimi de vC∆ = vC(∆) olur. t = ∆
olduğunda, A anahtarı da 2 konumuna alındığından kapasite boşalmaya başlayacaktır. t ≥ ∆
için, Şekil 3’de verilen eğri kullanılabilir; ancak bu eğriyi ∆ kadar ötelemek ve vC(0) yerine de
vC(∆) almak gerekir. Şekil 3 üzerinde yapılan bu işlem, (3) denkleminde t yerine (t - ∆) ve
vC(0) yerine de vC(∆) yazmaya denktir. Bu açıklamalar aşağıdaki matematiksel bağıntıyla
özetlenebilir;
vC(t) =
E(1 - e-t / RC )
;0≤t<∆
vC(0) e -(t - ∆) / RC
;t≥∆
(5)
(5) denkleminde, vC(∆) = E(1 – e -(t-∆) / RC) olmaktadır. E, R, C ve ∆ sayısal olarak verilince,
vC(∆) de sayısal olarak hesaplanabilir. Aynı şekilde vR(t) aşağıdaki gibi bulunabilir;
vR(t) =
E e –t/RC
vR(t) = ()
vc(0) e -(t - ∆) / RC
;0≤t<∆
;t≥∆
Şekil 1’deki devredeki e(t) kaynağının Şekil 6’daki gibi bir dikdörtgen dalga kaynağı
olduğunu düşünelim. C kapasitesinin uçlarındaki gerilimin değişimini incelemeye başlarken
R.C zaman sabitini, dikdörtgen dalganın periyoduyla karşılaştırmak gerekir.
39
e(t)
E
(a)
t
T1
T2
T
vC(t)
E
(b)
t
T1
T2
T3
vR(t)
(c)
t
Şekil 6
a) R.C << T ise, kapasite birinci darbe ile T1 süresince dolar ve T2 zaman aralığında ikinci
darbe gelene kadar boşalır. Zaman sabiti küçük olduğu için, T2 kadarlık zamanda kapasitenin
uçlarındaki gerilimin sıfıra ulaştığını kabul edebiliriz. Đkinci darbe ve daha sonraki darbelerde
olay aynı biçimde tekrarlanır; kapasitenin gerilimi periyodik olarak Şekil 6b’deki gibi
değişir.Bu gerilim, periyodik olduğu belirtilerek ve ∆ yerine de T1 konularak, (5) denklemiyle
ifade edilebilir. R direncinin uçlarındaki gerilimin değişimi ise, Şekil 6c’deki gibidir.
b) RC zaman sabiti, periyotla karşılaştırılabilir büyüklükte ise, vC(t)’nin değişimi Şekil 7’de
gösterildiği gibi olacaktır. Đlk darbe ile kapasite dolacak, darbe aralığında (T2 süresince)
kapasite tamamen boşalmadan ikinci darbe gelecek, tekrar kapasite dolacaktır. Bu durum
başlangıçtaki darbeler için bu şekilde devam edecektir. Belirli darbe sayısından sonra
kapasitenin uçlarındaki gerilimin değişimi periyodik hale gelecektir.
vC(t)
E2
E1
T1
T2
t
Tk
Şekil 7
40
Olayın periyodik olmaya başladığı an Tk başlangıç olarak alınabilir. Burada problem,
vC(t)’nin periyodik hale gelinceye kadar, darbelerle uçlarında E1 gerilimi bulunan ilk koşul
kapasitesinin bir darbe ile darbe süresince (T1) dolması ve darbe aralığında (T2) boşalması
olayıdır. O halde, olayı açıklamak için (2) ve (3) bağıntılarından yararlanılabilir;
e -t / RC E1+ E(1- e-t / RC )
vC(t) =
E2 e -( t - T1) / RC
; t ≥ T2
; 0 ≤ t < T1
(6)
t = T1 anında vC(T1) = E2 ve t = T1+T2 anında vC(T) = E1 olduğu düşünülürse, (6)
denkleminden;
E2 = E1e-T1/ RC + E( 1- e-T1 / RC )
E1 = E2 e -T2 / RC
(7)
elde edilir. Bunlardan da;
1- e-T1/ RC
e-T2 / RC - e-T / RC
E2 = E
E1 = E
(8)
1- e- T / RC
1- e- T / RC
bulunur. Dikdörtgen dalganın darbe süresi T1, periyodu T, genliği E, devredeki R ve C’nin
sayısal değerleri verilirse (8)’daki bağıntılar yardımıyla E1 ve E2 sayısal olarak hesaplanır ve
vC(t)’nin zamanla değişim ifadesini veren (6) denklemleri de sayısal olarak bulunabilir. vC(t)
belli olunca, vR(t) de şekil 8’deki gibi bulunabilir.
Şekil 8
c) RC >> T ise, (6) ve (8) denklemleri yine geçerlidir. Ancak, bu denklemlerdeki üstel
fonksiyonların hesabında bir yaklaşıklık mümkün olur. Daha açıkçası, RC >> T ise,
e-t / RC ≅ 1- t / RC
0 ≤ t < T1
e- ( t -T1) / RC ≅ 1 - ( t - T1) / RC
T1 ≤ t < T2
yazılabilir. Dolayısıyla, vC(t)’nin değişimi Şekil 9’da gösterildiği gibi doğrusal olacaktır.
41
vC(t)
t
Şekil 9.
RL Devresi :
Şekil 10’daki RL devresini gözönüne alalım.
R
+
e(t)
∼
di L
1
= -(R/L)iL(t) + e(t)
L
dt
L
(9)
Şekil 10.
(9) denkleminin yapısı, (1) denklemi ile aynıdır. RC devresi için yapılan bütün
incelemelerdeki yol uyarınca, RL devresi de incelebilir.
Şekil 11’de gösterilen devre, bir enerji dağıtım sistemini basitçe modellemekte kullanılabilir.
R, generatörden tüketiciye kadar yoldaki direnci (generatörün iç direnci, hat direnci vb.), L’de
yoldaki endüktansı (generatörün iç endüktansı, hat endüktansı gibi) göstermektedir. Şekil
10’daki devrede A ve B uçları kısa edilip, generatör kısa devre edilmiş sisteme bağlandığında
devredeki akımın zamanla değişimini inceleyelim. A ve B uçları kısa edilmiş Şekil 11’deki
devrenin durum denklemleri, (9) denkleminde verildiği gibi olacaktır. Burada, e(t)’nin
frekansı 50Hz olan bir kaynak olduğunu belirtelim.
R
L
A
+
e(t)
B
Şekil 11
e(t )= 2 E sin(ω t )
Bu durumda, (9) denkleminin özel çözümünün;
2E
i L (t ) =
sin(ω t - ψ )
Z
biçiminde olduğu gösterilebilir. Bu bağıntı da;
(10)
(11)
42
Z = R 2 + ω 2 L2
ψ = arctg(
(12)
ωL
)
R
olmaktadır. (9) denkleminin homojen kısmının çözümü,
i L (t ) = I h e − ( R/L ) t
olmaktadır. Tam çözüm ise;
i L (t ) = I h e −( R/L ) t +
2E
sin(ω t-ψ )
Z
(13)
(14)
olacaktır. Kısa devre olmadan önce endüktanstan bir akım geçmediği için, iL(0) = 0’dır. Bu ilk
koşul da (14) denkleminde yerine konursa,
2E
sinψ
(15)
I h (t) =
Z
elde edilir. O halde (14) denklemi;
2E
2E
i L (t ) = (
sinψ )e -( R/L ) t +
sin(ω t-ψ )
Z
Z
(16)
biçiminde yazılabilir. (16) denkleminde birinci terim, geçici çözüm; ikinci terim ise kalıcı
çözümü göstermektedir. (L/R)’nin beş katı kadar bir zaman sonra geçici çözümün etkisi ihmal
edilebilir. Kısa devrenin olduğu andan itibaren belirtilen zaman geçtikten sonra, devreden
efektif değeri (E/Z)’ye eşit olan kalıcı kısa devre akımı geçer.
(16) denklemiyle belirtilen iL(t), ωt = π/2 + ψ için en büyük değerine ulaşır. Akımın bu
değeri, kısa devre darbe akımı;
R π

2 E  ω L - ω L  2 +ψ  
Is =
1+
e
(17a)

Z 
Z


ya da,
(17b)
I s = 2 I′k′ x
ile ifade edilir. Burada Ik″, kalıcı kısa devre akımının değeri olup, E/Z’ye eşittir.
2

 - R  π +ψ  
 R 

 ω L 2 
x = 1 + 1 / 
(18)
 + 1 e  
ω
L




olmaktadır. (18) denkleminde görüldüğü gibi, x katsayısı, R/(ωL) değerine bağlı bir sabittir.
R=0 ise, x=2 olmaktadır. Bu halde, geçici çözümden dolayı devreden geçen akım, kalıcı kısa
devre akımının 2 katına kadar çıkmaktadır. Şebekedeki elemanları seçerken, kısa devrenin
başlangıcında akımın büyük değerlere ulaştığını göz önüne almanın gerektiği görülmektedir.
Burada, generatörün bir gerilim kaynağı ve ona seri bağlı bir iç direnç ve iç
endüktansla modellenmiş olduğunu hatırlayalım. Jeneratörü modelleyen eö(t) gerilim kaynağı
ve iç endüktansı (L’nin bir kısmı) kısa devre olayının başlamasından sonuna kadar aynı
kalmaz.
43
RLC Devresi:
Şekil 12’deki RLC devresini göz önüne alalım.
R
L
i L(0)
+
e(t) ~
C
vC(0)
Şekil 12
Bu devrenin durum denklemleri,
d
dt
vC(t)
0
(1/C)
vC(t)
=
i L(t)
0
+
(-1/L)
(-R/L)
i L(t)
e(t)
(19)
(1/L)
biçiminde elde edilir. Bu denklem sisteminin karakteristik denklemi,
p 2 + 2 ζ ωo p + ωo 2 = 0
(20)
olmaktadır. Burada ,
1
R C
, ζ =
(21)
LC
2 L
vC(0) = 0, iL(0) = 0 alınarak, her üç halde vC(t)’nin zamanla değişimi Şekil 13’te kabaca
çizilmiştir.
1
R
L
A
+
2
E
C
ωo =
Şekil 13
Şekil 14
Şekil 13’te görüldüğü gibi, her üç halde de kapasitenin uçlarındaki gerilim E’ye doğru
gitmektedir.
Şekil 12’deki devrede e(t)’nin E(u(t)-u(t-∆)) biçiminde bir darbe kaynağı olduğunu
düşünelim. Bu durumda devreyi Şekil 14’deki gibi yorumlamak incelemeye kolaylık
getirebilir. A anahtarı ∆ kadar bir süre (1) konumunda bırakıldıktan sonra, (2) konumuna
alınıyor. vC(0), iL(0) ilk koşullarının varolduğunu düşünelim. Anahtar (1) konumunda olduğu
sürece, 0 ≤ t < ∆ aralığında, ζ’nin değerine bağlı olarak, ya (23), ya (24), ya da (25)
denklemini kullanılabiliriz. t=∆ anında, iL(∆) ve vC(∆)’yı bu bağıntılar yardımıyla bulabiliriz.
Anahtar (2) konumunda iken, devrede kaynak olmadığı için yalnızca öz çözüm vardır. t > ∆
için, vC(t) ve iL(t)’yi bulmak için ζ’nin değerine göre (23), (24), (25) denklemlerinden biri
kullanılabilir. t >∆ için, vC(t) ve iL(t)’yi ifade etmek için, bu denklemlerde t yerine (t - ∆), vC
(0) ve iL(0) yerine, vC(∆) ve iL(∆), E yerine de sıfır koymak yeterlidir.
44
∆’nın yeterince büyük olduğunu düşünürsek, vC(t)’nin ζ’ye göre değişimi Şekil 15’deki
şekiller gibi olacaktır.
ζ < 1 için;
ζ = 1 için;
ζ > 1 için;
Şekil 15
Deney Öncesi Hazırlıklar :
1. Şekil 1, 9 ve 11’deki devrelerin eleman gerilim ve akımlarını, Laplace
dönüşümlerinden yararlanarak R, L, C ve v(t)’ye bağlı olarak bulunuz.
2. v(t) = u(t) ve v(t) = 1[u(t)-u(t-1)] için tüm eleman gerilimlerini ve akımlarını bulunuz
ve değişimlerini çiziniz.
3. Deneyin 1 ve 2. adımlarında uygulanacak olan işaretlerin periyotlarını hesaplayınız.
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki istenenleri sırasıyla bulunuz ve düzenli bir
şekilde raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
Malzeme ve Cihaz Listesi:
1. 68 Ω direnç 1 adet
2. 1 KΩ direnç 1 adet
3. 2 KΩ direnç 1 adet
4. 100 KΩ direnç 1 adet
5. 1mH endüktans 1 adet
6. 1 nF kapasite 1 adet
7. 100 nF kapasite 1 adet
8. Dijital Multimetre
9. Deney Seti (CADET I-IT)
10. Osiloskop ve iki adet prob
11. Pens, keski, montaj kablosu
45
Deneyin Yapılışı :
Şekil 16’ daki ölçme düzenini kurunuz.
C
Osilatör
Kare Dalga
L
1mH
R
Osiloskop
Şekil 16.
1. Ölçme düzeninde verilen L endüktansını çıkarıp, yerini kısa devre ediniz. Böylece elde
ettiğiniz RC devresinde kare dalga osilatörünün periyodunu T = 10RC, T= RC ve T=RC/10
değerlerine ayarlayarak, her üç hal için osiloskopta gördüğünüz şekilleri çiziniz. T ve osilatör
geriliminin tepe değerini kaydediniz. (R=1KΩ ve C=100nF alınız)
2. Şekil 16’da verilen devrede C kapasitesini çıkartıp yerini kısa devre ederek bir RL devresi
elde ediniz. Kare dalga osilatörünün periyodunu T = 10L/R, T = L/R ve T = L/(10R) alarak,
her üç için 1.aşamadaki işlemleri tekrarlayınız. (R=68Ω alınız)
3. Şekil 17’deki devrede, R>2 (L / C) , R<2 (L / C) ve R=2 (L / C) olacak biçimde R
direncine üç ayrı değer veriniz. Her üç hal için, kare dalga osilatörünün periyodunu büyük
seçerek(T=1ms), osiloskopta gördüğünüz dalga şekillerini çiziniz. Kare dalga osilatörünün
periyodunu küçük seçerek(T=0,01ms) deneyi tekrarlayınız. (C=1nF, L=1mH, R=2 (L / C)
için 2kΩ, R<2 (L / C) için 68Ω, R>2 (L / C) için 100KΩ kullanınız)
Sorular :
1) Deneyde kullandığınız eleman değerlerini gözönüne alarak ve “Teori” kısmında verilen
bilgileri kullanarak, yaptığınız deneyin (1) kısmı için vC(t) ve vR(t)’yi, (2) kısmı için iL(t)
ve vR(t)’yi, (3) kısmı için vC(t) ve vR(t)’yi teorik olarak hesaplayıp, değişimlerini çiziniz.
(3) kısım için yalnızca kaynak periyodunun büyük olması halini ele alınız. Deneyde elde
ettiğiniz sonuçları teorik sonuçlarla karşılaştırınız.
2) Seri RLC devresinde L = 0.5H, anlık gerilim v = 70.7sin(500t+30°)V ve ansal akım i =
1.5sin(500t)A’dır. R ve C değerlerini bulunuz. Hangi ω0 frekansında devre rezonansa
gelir?
3) R = 10Ω, L = 0.2H ve C = 40µF’tan oluşan seri devreye değişken frekansta gerilim
uygulanmıştır. Akımın gerilimin 30° önünde, gerilimle aynı fazda ve gerilimden 30°
geride olduğu f1, f0, f2 frekanslarını bulunuz.
4) Seri bir RLC devresinde L = 25mH ve C = 75µF’dır. Faz açısı ω = 2000 rad/s için 25°
geride ise, hangi frekans değerinde 25° ileri olur?
46
5) Yandaki devrede iç direnci RL olan bir
bobinle bir kapasitenin paralel birleşimi
görülmektedir. Devrenin rezonans
frekansını bulunuz.
RL
1/(jωC)
jωL
6) Aşağıdaki devreyi ω = 5000 rad/s
frekansında rezonansa sokacak C değerini bulunuz.
8Ω
8.34Ω
C
j6Ω
47
DENEY NO: 8
ĐŞLEMSEL KUVVETLENDĐRĐCĐ VE UYGULAMALARI
Deneyin Amacı:
Đşlemsel kuvvetlendirici elemanını tanıtmak ve bu elemanı kullanarak çeşitli uygulamalar
yapmaktır.
Genel Bilgiler:
Đşlemsel kuvvetlendirici yani opamp, analog devrelerde çeşitli matematiksel işlemleri
gerçekleştirmek amacı ile kullanılır. Bu deneyde çarpma, toplama, integral alma gibi
matematiksel işlemler incelenecektir. Đşlemsel kuvvetlendiriciler, çeşitli ölçü ve kontrol
sistemlerindeki regülatör, osilatör, logaritmik kuvvetlendirici, tepe dedektörü ve gerilim
karşılaştırıcısı gibi devrelerde de kullanılmaktadır.
Đşlemsel kuvvetlendiricinin gerilim kazancı çok yüksek olup farklı değerde olabilir. Tiplerine
bağlı olarak on binden, bir milyon arasıdır, fakat daha çok kazançlı olanları da bulunabilir.
Giriş dirençleri oldukça büyüktür: 103 ile 1015 Ohm arasındadır. Çıkış dirençleri ise çok küçük
olup 1 ile 1000 Ohm arasındadır. Frekans sınırları DC’den başlayıp, GHZ mertebelerine kadar
çıkmaktadır.
Đşlemsel yükseltecin içinde yaklaşık 30 adet transistor, 10 adet direnç ve birkaç adet diyot
bulunur. Yapısı yarı iletken entegre şeklinde olup hacimleri küçük ve maliyetleri oldukça
düşüktür. Güç sarfiyatları az olup, kararlı oldukları için oldukça karmaşık sistemlerde çok
sayıda kullanılabilirler. /1/
Đdeal işlemsel kuvvetlendirici :
ip = 0 , in = 0 , vp= vn
vn
(1)
vo
vp
Ro→0
vn(t)
vo(t)
Ri→∞
A(vp-vn)
vp(t)
Ref
Ref
a) Đşlemsel kuvvetlendiricinin
devre sembolü
b)Đşlemsel kuvvetlendiricinin bağımlı gerilim
kaynağı ve dirençlerden oluşmuş küçük işaret
eşdeğeri
vn
vo
vp
Ref
Şekil 1. Đşlemsel kuvvetlendiricinin sembolü
ve küçük işaret eşdeğer ve fiziksel şeması
c) LM741 Đşlemsel yükseltecin
fiziksel bağlantıları
48
Đşlemsel yükseltecin iki giriş ve bir çıkış ucu vardır. Besleme kaynağı genellikle simetrik
olup, buralara +V ve –V gerilimleri uygulanır.
OPAMP Uygulamaları:
Gerilim Takipçisi (Voltage follower, Buffer):
Đşlemsel kuvvetlendiricinin sonsuza yaklaşan giriş direnci ve sıfıra yaklaşan çıkış direnci
sayesinde Şekil 2’deki devre yardımıyla gerilim takipçisi devresi gerçekleştirilir.
vo(t)
vi(t)
Şekil 2. Gerilim takipçisi
Gerilim takipçisinde: vo (t ) = vi (t ) ⇒ H V =
Vo
=1
Vi
Gerilim takipçisinin giriş direnci çok büyük olduğu için kendisinden önceki devreyi
yüklemez. Çıkış direnci çok küçük olduğundan, kendisinden sonraki devre için ideal gerilim
kaynağı gibi davranır. Kazancı da birdir. Bu özelliklerinden dolayı buna izolasyon
amplifikatörü veya buffer adı da verilir.
Đşaret Değiştiren (Eviren) Kuvvetlendirici (Inverting Amplifier):
Bu devre Şekil 3’deki gibidir. Burada Ri giriş direnci, Rf geri besleme direnci olup, devrenin
girişine vi(t) gerilim kaynağı bağlandığında, çıkıştaki vo(t) gerilimi aşağıdaki şekilde bulunur.
Rf
Ri
vi(t)
vo(t)
Şekil 3. Eviren Kuvvetlendirici
Rf
Çıkış gerilimi:
vo (t ) = −
vi (t )
Ri
Rf
v (t )
Gerilim Kazancı = H v = o = −
vi (t )
Ri
(3)
(4)
49
Đşaret Değiştirmeyen (Evirmeyen) Kuvvetlendirici (Non-inverting Amplifier):
vo(t)
vi(t)
RB
RA
Şekil 4. Evirmeyen Kuvvetlendirici
 R 
(5)
vo (t ) = 1 + B vi (t )
 RA 
v (t )
R
Gerilim Kazancı = H v = o
(6)
= 1+ B
vi (t )
RA
Görüldüğü gibi evirmeyen kuvvetlendirici için gerilim kazancı her zaman 1’den büyüktür.
Devreden hareketle;
Toplama Devresi:
Şekil 5’deki devre ile iki ya da daha çok bağımsız giriş işaretinin toplamı (daha açıkçası lineer
kombinezonu) elde edilir. Bu devre, aynı zamanda çok girişli eviren toplayıcı devresidir.
Rf
R1
R2
v1(t)
vo(t)
v2(t)
Şekil 5. Toplama Devresi
Çıkış işaretinin denklemi iki giriş işareti için aşağıdaki şekilde olacaktır.
Rf
Rf

vo (t ) = − 
v1 (t ) +
v 2 (t )
R2
 R1

Genel olarak k tane giriş için aşağıdaki ifade yazılabilir.
k
k
1
vo (t ) = − R f ∑ vi (t ) = − R f ∑ Gi vi (t )
i =1 Ri
i =1
(7)
(8)
Đntegral Alıcı Devre (Integrater)
Şekil 3’deki eviren kuvvetlendirici devresinde Rf yerine C elemanı konularak Şekil 6’daki
integratör devresi elde edilir. Çıkış gerilimi, giriş geriliminin integrali biçiminde olur.
t
1
vo (t ) = −
vi (t )dt
R A C ∫0
(9)
50
C
RA
vi(t)
vo(t)
Şekil 6. Đntegral Alıcı Devre
Şekil 6’deki devrede giriş off-set geriliminin işlemsel kuvvetlendiriciyi bir süre sonra doyuma
götürmesini engellemek için, C kapasitesine paralel bir RS direnci bağlanır. (Off-set gerilimi:
Đşlemsel kuvvetlendiricilerde karşılaşılan sorunlardan birisi de giriş gerilimlerinin sıfır
olmasına rağmen, çıkış geriliminin sıfır olmamasıdır. Değişken işaretler kuvvetlendirilirken
önemli olmayan bu durum, özellikle doğru gerilim kuvvetlendiricilerinde ve büyük kazançlı
işlemsel kuvvetlendirici ile kurulan devrelerde sorun olur. Off-set gerilimi olarak adlandırılan
bu gerilim, özellikle giriş katını oluşturan elemanların tam olarak özdeş olamaması ve eleman
toleranslarından kaynaklanır.) Ayrıca giriş kutuplama akımlarının eşit olamayışından doğacak
off-set gerilimini ve bu gerilimin etkilerini gidermek için + uç ile toprak arsına RA direnci
bağlanır.
C
RS
RA
vi(t)
vo(t)
RA
Şekil 7. Đntegral Alıcı Devre
Devrenin bir integral alıcı olarak görev yapabilmesi için girişine uygulanan işaretin frekansı
1
olmalıdır.
fi > fc =
2π RS C
R
fi < fC olduğunda, devre eviren yükselteç olarak çalışır ve kazanç, S olur.
RA
Nonlineer Op – Amp Uygulaması (Karşılaştırıcı Devresi)
Karşılaştırıcı, bir giriş gerilimi ile bir referans gerilimini karşılaştıran devredir.
Karşılaştırıcının çıkışı giriş geriliminin referans geriliminden aşağıda yada yukarıda olduğunu
ifade eder. Giriş sinyali referans geriliminden büyükse çıkış pozitif besleme gerilimine,
küçükse negatif besleme gerilimine gider. Basit bir karşılaştırıcı devresi aşağıda verilmiştir.
Şekil 8. Karşılaştırıcı Devresi
51
Đşlemsel Kuvvetlendiricinin Seçimi:
Önceki bölümde verilen devreler birçok işlemsel kuvvetlendirici kullanılarak
gerçekleştirilebilir. Bunlar için en sık rastlanan ve genel amaçlı bir işlemsel kuvvetlendirici
olan 741 entegresi uygundur.
741 için açık çevrim kazancının frekansla değişimi Şekil 9’da verilmiştir. Đşlemsel
kuvvetlendiricinin açık çevrim kazancı, istenen en yüksek frekans için devrenin gerilim
kazancından, en az 20 katı olmalıdır. Örneğin, 10kHz’lik işaretleri kuvvetlendirecek bir
devrede 741 işlemsel kuvvetlendirici elemanı kullanılacaksa Şekil 9’da görüldüğü gibi, 741’in
10kHz’deki açık çevrim kazancı yaklaşık olarak 100 olacaktır. Demek ki, kuvvetlendirici
devresinin gerilim kazancı 5’den küçük olmalıdır.
6
Kazanç 10
5
10
4
10
3
10
2
10
10
1
1
10
2
10
3
10
4
10
5
10
6
10
7
10
Frekans
Şekil 9. Açık Çevrim Kazancının Frekansla Değişimi
Đşlemsel kuvvetlendirici seçiminde diğer bir faktör, yükselme eğimi (Slew rate)’dir. Yükselme
 dv (t ) 
eğimi SR, çıkışın değişebildiği maksimum değer olarak tanımlanır. SR =  o 
 dt  max
741 için 0.5 V/µs’dir. Tepeden tepeye genliği 1 V olan sinüzoidal bir gerilim uygulandığında
741’in en yüksek çalışma frekansı, fMAX = [(0.5 V/µs) / 2*1 V)] = 250 kHz olur.
Sonuç olarak, girişteki gerilimin genliği artırıldığında, işlemsel kuvvetlendiricinin
çalışabileceği maksimum frekans değeri azalacaktır. 318 işlemsel kuvvetlendiricisinin
gerilimin frekansla değişimi 70 V/µs’dir. Dolayısıyla, tepeden tepeye gerilimi 1V olan
sinüzoidal bir gerilim uygulandığında 318’in en yüksek çalışma frekansı 35 MHz olur. Ancak
318’in fiyatı da bu oranda yüksektir.
Deney Öncesi Hazırlıklar:
1. LM741 tümdevresinin katolog bilgilerini inceleyiniz.
2. Deneyde kullanacağınız devreler için tabloda verilen direnç değerlerini kullanarak çıkış
gerilimlerini ve kazançları teorik olarak hesaplayınız. (Đşlemsel kuvvetlendiricileri ideal
alınız.)
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki istenenleri sırasıyla bulunuz ve düzenli bir
şekilde raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
52
Malzeme ve Cihaz Listesi:
1. LM741 Đşlemsel Yük. 2 adet
2. 10 kΩ direnç 3 adet
3. 15 kΩ, 27 kΩ, 47 kΩ ,100 kΩ
4. 1 kΩ direnç 2 adet
5. 1 adet 22nF kapasite
6. Bir adet milimetrik kağıt
7. Dijital Multimetre
8. Deney Seti (CADET I-IT)
9. Osiloskop ve iki adet prob
10. Pens, keski, montaj kablo
direnç 1’er adet
Deney Sırasında Yapılacaklar:
Đşaret Değiştiren Kuvvetlendirici Deneyi:
RB
12 V
10 kΩ
RA
vi(t)
Sinüs
Dalga
2
7
3
741
4
10 kΩ
6
vo(t)
1.Kanal
Osiloskop
12 V
2.Kanal
a) 7 ve 4 numaralı uçlar ile toprak arasına, sırasıyla +12 V ve –12 V doğru gerilim
uygulayınız.
b) Osiloskobun CH1 ve CH2 kanallarını uygun konuma getiriniz.
c) Sinüzoidal kaynak gerilimini (tepeden tepeye) 0.2 V’a, frekansını 1 kHz’e ayarlayınız.
d) vi(t) ve vo(t) gerilimlerinin zamanla değişimini çiziniz ve aralarındaki farkın nedenini
(genlik ve faz) olarak açıklayınız.
e) Girişteki vi(t) sinüzoidal geriliminin tepeden tepeye 200 mV olan değerini değiştirmeden
farklı RB direnç değerleri için aşağıdaki tabloyu doldurunuz.
RB (kΩ)
15
47
Tepeden Tepeye VO
Kazanç
53
Đşaret Değiştirmeyen Kuvvetlendirici Devresi:
Sinüs
Dalga
vi(t)
Osiloskop
3
2
6
741
10 kΩ
vo(t)
RB
10 kΩ
RA
1.Ka
2.Kanal
a) Önceki deneydeki ilk dört adımı sırasıyla tekrarlayınız.
b) Burada Gerilim Kazancı = 1+RB/RA=2’dir. Girişi (tepeden tepeye) 200mV olan sinüzoidal
bir gerilim alarak, farklı RB değerleri için aşağıdaki tabloyu doldurunuz.
RB (kΩ)
Tepeden Tepeye VO
Kazanç
27
100
Toplama Devresi Deneyi:
a) 7 ve 4 numaralı bacakları ile toprak arasına sırasıyla +12V ve –12 V gerilim uygulayınız.
b) Sinüzoidal kaynak gerilimin tepeden tepeye 1V ve frekansı 5 kHz olacak şekilde
ayarlayınız.
c) V1(t) kare dalga gerilimini tepeden tepeye 2V ve frekansı 1kHz olacak şekilde ayarlayınız.
d) vo(t) gerilimini milimetrik kağıda çiziniz ve yorumlayınız.
Đntegral Alıcı Devre Deneyi:
C
22 nF
RS
Kare
Dalga
vi(t)
RA
1 KΩ
RA
10 KΩ
Osiloskop
2
3
741
6
vo(t)
1.Ka
2.Kanal
1 KΩ
54
a) 7 ve 4 numaralı bacakları ile toprak arasına sırasıyla +12V ve –12 V gerilim uygulayınız.
b) Osiloskobun CH1 ve CH2 kanallarını uygun konumuna getiriniz.
c) Đşaret üreteci ile girişe (tepeden tepeye) 1 V ve frekansı 5000 Hz olan bir kare dalga
uygulayınız. Çıkış ve giriş işaretlerini çiziniz. Çıkış işareti girişin integrali midir?
d) Kaynak frekansı artırıldığında vo(t) çıkış geriliminin genliğinin küçüldüğünü görünüz ve
bunun nedenini açıklayınız.
e) Kaynak frekansını 100 Hz’e getiriniz. Bu durumda, çıkış geriliminin üçgen dalga
biçiminden daha çok kare dalgaya benzediğini görmelisiniz. Bu arada çıkış gerilimi de
artar. Neden?
Karşılaştırıcı Devresi
a) 7 ve 4 numaralı bacakları ile toprak arasına sırasıyla +12V ve –12 V gerilim uygulayınız.
b) Đşaret üreteci ile girişe tepe değeri 6V ve frekansı 1kHz olan bir sinüs uygulayınız.
c) Çıkış işaretini gözlemleyip, yorumlayınız.
Sorular:
1. Đşaret değiştiren kuvvetlendiricinin giriş ve çıkış gerilimleri arasında kaç derecelik faz
farkı vardır?
2. (9) ifadesini Şekil 6’daki integral alıcı devreyi inceleyerek elde ediniz.
3. Gerilimin zamanla değişim oranı (SR) 0.25 V/µs olan bir işlemsel kuvvetlendiricinin
girişine tepeden tepeye genliği 2 V olan bir işaret uygulanmıştır. Đşlemsel kuvvetlendiricinin
en yüksek çalışma frekansı ne olur?
4. Aşağıdaki devrede işlemsel kuvvetlendiriciyi ideal alarak vo (t) çıkış gerilimini bulunuz.
270 kΩ
2,7 kΩ
vi(t)
∼
vo(t)
120 µV
55
56
57
DENEY NO: 9
RLC DEVRELERĐNĐN SĐNÜSOĐDAL SÜREKLĐ HALDE
ĐNCELENMESĐ
Deneyin Amacı:
Sinüsoidal sürekli halde RL, RC ve RLC devrelerinin incelenmesidir.
Genel Bilgiler:
Sinüsoidal sürekli halde 1-kapılı devrelere ilişkin giriş fonksiyonları aşağıdaki gibi tanımlanır;
R: Rezistans
V
Empedans:
Z = = R + jX
X: Reaktans
I
G: Kondüktans
I
1
B: Süseptans
Y = = = G + jB
Admitans:
V Z
Devredeki elemanların gerilim ve akımları SSH’de fazörel olarak toplanır.
R, L ve C elemanlarının fazörlerle elde edilen akım gerilim ilişkileri aşağıdaki gibidir:
1. R elemanına Şekil 1’deki gibi v(t ) = Vm cos(ω t ) sinüsoidal işareti uygulandığında R
elemanı üzerindeki akım ve gerilimin zamana göre ifadesi ve grafiği aşağıdaki gibidir.
v(t )
V
⇒I=
R
R
Şekil 1. Direnç elemanı
Buna göre; R elemanı üzerindeki gerilim ile akım arasında faz farkı yoktur. Ancak aynı
durum L ve C elemanları için söz konusu değildir.
i (t ) =
2. L elemanına Şekil 2’deki gibi v(t ) = Vm cos(ω t ) şeklinde sinüsoidal bir işaret
uygulandığında, L üzerindeki gerilim ve akımın değişimi Şekil 2’deki denklem ile ifade
edilmiştir. L elemanının empedansı ω ile doğru orantılıdır.
v(t ) = L
di (t )
⇒ V = jω LI ⇒ Z L = jωL
dt
Şekil 2. Endüktans elemanı
58
Grafikten ve fazör ifadeden anlaşılacağı gibi akım ile gerilim arasında 90° faz farkı vardır.
Gerilim, akımın 90° ilerisindedir.
3. C elemanına Şekil 3’deki gibi v(t ) = Vm cos(ω t ) şeklinde sinüsoidal bir işaret
uygulandığında C üzerinden geçen akımın zamanla değişim ifadesi ve grafiği aşağıdaki gibi
olur. Bu ifadeden ve grafikten anlaşıldığı gibi akım ile gerilim arasında 90° faz farkı vardır.
Gerilim, akımın 90° gerisindedir. C elemanının empedansı ω ile ters orantılıdır.
i (t ) = C
dv(t )
−j
⇒ I = jω CV ⇒ Z C =
dt
ωC
Şekil 3. Kapasite elemanı
59
Faz farkının pratik olarak ölçülmesi:
Gerilim transfer fonksiyonunun fazı, çıkış ve giriş işaretleri arasındaki faz farkına eşittir.
θ1 ve θ2 sırası ile giriş ve çıkış işaretlerinin fazları olmak üzere;
∠H(jw) =ϕ(w)=θ2-θ1 = ω(t2-t1) = ω ∆t rad
ifadesiyle gerilim transfer fonksiyonunun fazı bulunabilir.
Đki işaret arasındaki ϕ faz farkının bulunması için ∆t süresinin bilinmesi gerekir. Şekil 5’de,
osiloskop ekranında gözlenen iki işaret arasındaki ∆t zaman aralıkları gösterilmiştir.
Osiloskobun Time/Div seçici anahtarının (komütatör) değerinden yararlanarak ∆t zaman
aralığı kolaylıkla ölçülebilir.
Böylelikle, girişe uygulanan kaynağın frekansı belli olduğundan ve ∆t süresi de ölçme yoluyla
bulunarak, iki işaret arasındaki faz farkı ϕ=ω.∆t [rad] eşitliğiyle kolaylıkla hesaplanır.
2π radyan 360 derece olduğundan, ϕ=(180/π)ω.∆t [derece] olarak da yazılabilir. Eğer
θ2>θ1 ise ϕ>0 olup çıkış işareti girişten ϕ açısı kadar ileride, θ2<θ1 ise ϕ<0 olup çıkış işareti
girişten ϕ açısı kadar geridedir. ϕ açısının pozitif veya negatif olması konusunda yanılgıya
Sekil 5. ∆t süresinin ölçülmesi
düşmemek için giriş işaretinin fazı, başlangıç fazı olarak kabul edilmeli (θ1=0 derece yani
t1=0 almak kolaylık sağlar) ve osiloskobun iç-tetikleme (INT-TRIG) anahtarı da, giriş
işaretinin osiloskoba uygulandığı kanala göre seçilmelidir. Deneyde giriş işareti CH1 kanalına
uygulanacağından INT-TRIG anahtarı da CH1 olarak seçilecektir. Ölçme işlemlerinde hataya
düşmemek için önerilen en emin yol; teorik çalışmanın yapılarak sonuçların kontrol
edilmesidir.
Osiloskop ile genlik ve zaman/periyot ölçmelerinde meydana gelebilecek okuma hatasını
minimuma indirgemek için aşağıdaki hususlar göz önünde tutulmalıdır:
a) Genlik Ölçülmesi: Đşaretin tepeden tepeye genliği osiloskop ekranına sığacak biçimde
(Şekil 4’deki gibi) VOLTS/DIV komütatörü ayarlanmalıdır.
b) Zaman Ölçülmesi: Đşaretin bir periyodunu osiloskop ekranına sığacak biçimde (Şekil 5’te
ki gibi) TIME/DIV komütatörü ayarlanmalıdır.
Deney Öncesi Hazırlıklar:
Deneyde kurulacak devrelerle ilgili hesaplamaları yapınız. RLC devresinin rezonans
frekansını her iki endüktans değeri için hesaplayınız. Tablo 1-2-3’ün deney öncesi hesap
sütunlarını doldurunuz.
Deney Öncesi Hazırlık Raporunda Đstenenler:
ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz.
60
1.
2.
3.
4.
5.
6.
1kΩ direnç 1 adet
1mH endüktans 1 adet
330nF kondansatör 1 adet
Osiloskop ve iki adet prob
Deney seti (CADET-I ve II)
Pens, keski, montaj kablosu
Deney Sırasında Yapılacaklar:
1. Şekil 6’daki RL devresini kurun. Kaynak frekansını f1=5KHz’e, genliğini tepeden tepeye
2V’a ayarlayın. Osiloskopta v(t) ile vR(t) arasındaki zaman kaymasını ve vR(t)’ye ilişkin
maksimum değeri okuyup Tablo 1’e yazın. v(t) ile vR(t) arasındaki faz farkını hesaplayıp Tablo
1’de yerine yazın. R ile L’nin yerini değiştirip aynı işlemleri L için tekrarlayın.
V = VR + jVL eşitliğinin doğruluğunu fazör diyagramı çizerek gösterin.
VR = RI, VL = XLI, V = ZI eşitliklerinden yararlanarak I, XL, Z’nin fazör diyagramlarını çizerek
∠Z’yi hesaplayın. Deney öncesi hesaplanan değerlerle karşılaştırın.
Aynı işlemleri; kaynak frekansını tabloda belirtilen f2=40KHz değerlerine getirerek tekrarlayın.
Frekansın değişimine göre XL ve Z’nin değişimini yorumlayın.
v(t ) = cos(2πft ) Volt
R=1kΩ
L=1mH
Şekil 6.
Tablo 1
Frekans Deney Öncesi Hesap
XL Z
∠Z
5 kHz
40kHz
VR
Ölçüm
∆tR VL
∆tL
ϕR
ϕL
Hesap
I
XL
Z ∠Z
2. Şekil 7’deki RC devresini kurup, kaynak frekansını f1=500 Hz’e, genliğini tepeden tepeye
2V’a ayarlayın. Osiloskopta v(t) ile vR(t) arasındaki zaman kaymasını ve vR(t)’ye ilişkin
maksimum değeri okuyup Tablo 2’ye yazın. v(t) ile vR(t) arasındaki faz farkını hesaplayıp
tabloda yerine yazın. R ile C nin yerini değiştirip aynı işlemleri C için tekrarlayın.
V = VR + jVC eşitliğinin doğruluğunu fazör diyagramı çizerek gösterin.
I, XC, Z ve ∠Z değerlerini 1. bölümdeki gibi hesaplayıp Tablo 2’deki yerlerine yazın. Deney
öncesi hesaplanan değerlerle karşılaştırın. R, XC, Z’nin fazör diyagramını çizin. Aynı işlemleri
kaynak frekansını tabloda belirtilen f2=40kHz değerlerine getirerek tekrarlayın. Frekansın
değişimine göre XC ve Z’nin değişimini yorumlayın.
61
v(t ) = cos(2πft ) Volt
R=1kΩ
C=330 nF
Şekil 7.
Tablo 2
Frekans Deney Öncesi Hesap
f
XC
Z
∠Z
500Hz
40kHz
VR
Ölçüm
∆tR VC
∆tC
ϕR
ϕC
Hesap
I
XC
Z ∠Z
3. Şekil 8’deki seri RLC devresini kurun. Kaynak frekansını devrenin rezonans frekansının onda
birine (fR/10), genliğini tepeden tepeye 2 V’a ayarlayın.
• Osiloskopta v(t) ile vR(t) arasındaki zaman kayması (∆tR) ve vR(t)’ye ilişkin maksimum
değeri ölçüp, Tablo 3’e yazın.
v(t) ile vR(t) arasındaki faz farkını hesaplayıp Tablo 2’ye yazın.
• R ile L’nin yerini değiştirip aynı işlemleri endüktans elemanı için tekrarlayın.
• L ile C’nin yeri değiştirip, seri RLC devresinde aynı işlemleri kapasite elemanı için
tekrarlayın.
V = VR + j(VL-VC) eşitliğinin doğruluğunu fazör diyagramı çizerek gösterin.
I, XC, XL, Z ve ∠Z değerlerini hesaplayıp Tablo 3’deki yerlerine yazın. Deney öncesi
hesaplanan değerlerle karşılaştırın.
Aynı işlemleri kaynak frekansını tabloda belirtilen f2=fR, f3=10fR değerlerine getirerek
tekrarlayın. Frekansın değişimine göre XC, XL ve Z’nin değişimini yorumlayın.
v(t ) = cos(2πft ) Volt
R=1kΩ
L=1mH
C=330 nF
Şekil 8
Tablo 3
fR=
DÖH
Z ∠Z

fR/10
fR
10fR
VR
∆tR
Ölçüm
VL ∆tL
VC
∆tC
ϕR
ϕL
ϕC
Hesap
I XL
XC Z ∠Z
62
Sorular:
1.
a) Şekil 9’da verilen devrenin H(jω) transfer
fonksiyonunu, H(jω) genlik ve ∠H(jω) faz
fonksiyonlarını bulup bu fonksiyonların
frekansa göre değişimlerini yorumlayınız.
b) vi (t ) = 2 cos(2πft ) Volt, L=5mH, C=250pF,
R=200Ω ve f=100Hz ve f=100KHz olması
halinde çıkışın genlik ve fazını bulunuz.
Şekil 9.
2. Şekil 10a ve b’de verilen devrelerin H(jω) transfer fonksiyonunu elemanlara göre parametrik
olarak bulunuz.
f1=100Hz, f1=5KHz, f1=250KHz için
H(jω)genlik ve ∠H(jω) faz
fonksiyonlarını hesaplayınız.
a) R1=R2=5 KΩ
C1=C2=100 nF
vi(t)=Vmsin(2πft)
b) R3=R4=1 KΩ
C3=10 nF
L1=10 mH
vi(t)=Vmsin(2πft)
Şekil 10.
63
DENEY NO: 10
SPICE KULLANARAK FĐLTRE DEVRELERĐNĐN
DOMENĐNDE ANALĐZĐ VE SĐMÜLASYONU
ZAMAN
VE
FREKANS
Deneyin Amacı:
Pasif ve aktif filtre devrelerinin Orcad PSpice A/D kullanarak simülasyonu ve dışarıdan
verilen bazı uyarılara karşı bu devrelerin yanıtlarının programa hesaplatılıp çizdirilmesi suretiyle
simülasyon yapmanın, devre kurmaya göre avantajları ve dezavantajlarının öğrenilmesi.
Spice Hakkında Genel Bilgiler:
Bilgisayarla devre simülasyonu, elektronik devrelerin ve sistemlerin tasarımında en
önemli adımlardan biridir. Bilgisayar destekli tasarımın veya elektronik devrelerin bilgisayar ile
simüle edilmesinin sağladığı en büyük yarar, tasarımcının laboratuar ortamında elde etmesinin
uzun süre alacağı sonuçların simülasyon ile kolayca görebilmesidir. Devre tasarımcısı, bilgisayar
kullanarak gerçek bir devrede ölçü probunun yaptığı gibi devreyi yüklemeksizin akım ve gerilim
dalga şekillerini ve frekans cevabını izleyebilir; doğru gerilim seviyelerini bozmadan bir
geribesleme çevrimini açabilir, bir deney plaketinin getireceği parazitik etkiler olmaksızın
elektronik bir sistemin yüksek frekanslardaki davranışını inceleyebilir. Başka bir ifadeyle
tasarımcı, laboratuar çalışmalarına başlamadan, tasarladığı devrenin davranışını bilgisayar
yardımıyla inceleme olanağı elde etmektedir.
SPICE(Simulation Package with Integrated Circuit Emphasis) ilk olarak Berkeley’deki
Kaliforniya Üniversitesinde geliştirilmiştir. Analog devre simulasyonu açısından dünya standardı
olan programın birçok ticari türevinden bir tanesi MicroSim şirketince yapılan PSpice
programıdır. Daha sonraları PSpice tabanlı bir çok görsel devre tasarım programları
geliştirilmiştir.
Spice simülasyonu için, analizi yapılacak devrenin giriş dosyası üzerinden tanımlanması
gerekir. Devrenin programa tanıtılabilmesi için düğümlerin numaralanması ve elemanların hangi
düğümlerin arasında bulunduğunun belirtilmesi gerekir. Düğüm numaraları keyfi olarak
verilebilir. Referans düğümü “0” ile gösterilmelidir.
SPICE programında üç değişik tipte satır bulunmaktadır: ELEMAN SATIRI, KOMUT
SATIRI ve YORUM SATIRI.
ELEMAN SATIRLARI: Belirli bir devredeki bir devre elemanını tanımlar. O halde her bir
devre elemanı için bir komut satırı mevcuttur. Bir devre elemanını tanımlamak için komut satırı
şu bilgileri içermelidir: eleman tipi için gerekli sembol, o devredeki belirli ismi, devredeki
konumu ve değeri(mevcutsa parametreleriyle birlikte örn. bir transistör varsa).
Örneğin, bir direnç elemanı için komut satırı R (veya r ) sembolü ile başlamalıdır. Daha sonra
devredeki belirli ismi şu şekilde eklenebilir: R yük , R 1 , R 2 , R 3 ( veya ryük , r1 ), vs. Örnek:
10Ω, 10kΩ veya 10MΩ değerinde üçüncü ve beşinci düğümler arasına bağlanmış R L1 direncini
tanımlayan komut satırı yazılsın.
Bu satırlar her bir direnç değeri için şu şekilde yazılmalıdır:
RL1 3 5 10
RL1 3 5 10k
RL1 3 5 1meg
64
Bu satırlarda R eleman tipini belirtirken L1 elemanın o devredeki belirli ismini, 3. ve 5.
düğümler devredeki konumunu, 10, 10k ve 10meg ise eleman değerini belirtir. Elemanın birimini
yani ohm(Kondansatör için F(Farad) veya endüktans için H(Henry)) ise isteğe bağlıdır.
KOMUT SATIRLARI: Bir ‘.’ (nokta) sembolü ile başlar. Hangi tip analiz yapılacağını
belirleyen komutlar komut satırlarına örnek olarak gösterilebilirler:
.TRAN 1ms 50ms ; zamanda 50 ms boyunca analiz yapar.(Değişken zamandır.)Her 1ms’de bir
çıkış dosyasına(.out) veri gönderir;
.AC LIN 11 100Hz 200Hz ; frekansta 100Hz’den 200Hz’e analiz yapar.(Değişken frekanstır.) Bu
frekans aralığında 11 nokta alır.
.PROBE ; grafik işlemcisini çağırır.
.END ; programın bittiğini gösterir.
YORUM SATIRLARI: Bir ‘*’ işareti başlar. Kaynak dosyaları başlık satırı olan özel bir komut
satırı ile başlar, örn. *Toplama devresi simulasyonu
Simulasyon yapıldığında SPICE programındaki hesap sonuçları dosya_adı.dat dosyasına
konur. Bu dosya SPICE tarafından varsayılan olarak oluşturulur. Eğer sonuçlar saklanmak
isteniyorsa SPICE tarafından oluşturulan dosya_adı.dat ve dosya_adı.cir dosyaları alınmalıdır.
Ölçek ve birim kısaltmaları:
Büyük veya küçük sayıları ifade etmek için standart metrik kısaltmalar PSpice
programında değiştirilmiştir. Çünkü PSpice programı yapısı itibariyle büyük küçük harfe duyarlı
değildir. Aynı zamanda Latin harfleri de yapısında mevcut değildir. Mesela standartta 106 sayısı
için Mega(M), 10-3 sayısı için mili(m) kullanılır. Fakat PSpice’ta küçük büyük harf ayrımı
olmadığı için mega(meg) kısaltması kullanılmıştır. Aşağıda PSpice’ta kullanılan bazı kısaltmalar
verilmiştir.
F
P
N
U
M
K
MEG
G
T
femto
pico
nano
micro
mili
kilo
mega
giga
tera
10-15
10-12
10-9
10-6
10-3
103
106
109
1012
V: Volt
A: Amper
Hz: Hertz
Ohm: Ohm
H: Henry
F: Farad
DEG: Derece
DEC: Dekad
Pasif Elemanlar (Direnç, Kondansatör, Endüktans):
Pasif elemanlar belirtilirken, sırasıyla eleman tipi için gerekli sembol, o devredeki
belirli ismi, devredeki konumu(Hangi düğümlere bağlı olduğu) ve değeri yazılır.
Direnç Elemanı :
R1
1
0
10K
Kapasite Elemanı:
C5
10
15
100U
65
Endüktans Elemanı:
L3
12
0
5M
Bağımsız Kaynaklar:
DC Kaynak: “DC Analiz”, “Transient Analiz” gerçekleştirilirken kullanılır.
Gerilim veya Akım Kaynağı Devredeki konumu Türü Değeri
V1
1
0
dc
5V
I5
3
4
dc
2A
AC Kaynak: Sadece “AC Analiz” yapılırken kullanılan kaynak türüdür. Analiz sırasında AC
kaynağın frekansı belirlenen değerler arasında değiştirilerek devrenin frekans karakteristiği elde
edilir. Bundan dolayı kaynağın frekansı kaynak özelliklerinde yoktur. Sadece kaynağın genlik
değeri belirtilir.
Gerilim veya Akım Kaynağı Devredeki konumu Türü Değeri
Vac2
3
6
ac
1V
Iac1
2
8
ac
2mA
Sinüsoidal Kaynak: “Transient Analiz” gerçekleştirilirken kullanılan kaynak türüdür. Đstenilen
frekansta ve genlikte sinüsoidal işaret üretilir. Đşarete belli bir ofset değeri de eklenebilir.
Gerilim veya Akım Kaynağı Devredeki konumu SIN(Voffset
Vpeak Frekans)
V1
3
6
sin(0
5
1khz )
I10
2
8
SIN(0.5 1m 100meghz )
Darbe Kaynağı: Transient Analiz” gerçekleştirilirken kullanılan kaynak türüdür. Kaynağın
kullanılışı aşağıda verilmiştir.
Gerilim veya Akım Kaynağı Devredeki konumu PULSE(V1 V2 TD TR TF PW PER )
Vgiris
2
0
PULSE(0 5 0 1n 1n 0.5m 1m)
Iabc
2
8
PULSE(1m 3m 1u 1n 1n 0.5u 1u)
Burada,
V1: Başlangıç değeri(volt)
V2: Darbe değeri(volt)
TD: gecikme zamanı(saniye)
TR: Yükselme zamanı(saniye)
TF: Düşme zamanı(saniye)
PW: Darbe genişliği(saniye)
PER: Periyot(saniye)
Bu özelliklerin neler olduğu Şekil 1 ile belirtilmiştir.
66
Şekil 1.
Darbe kaynağı ile periyodik olmayan işaretler de oluşturulabilir. Bunun için “PER” özelliği boş
bırakılmalıdır. Birim basamak fonksiyonunu da darbe kaynağı ile elde edebiliriz. Bunun için
“PW” özelliğini çok büyük seçilir, “PER” özelliği kullanılmaz ve simülasyon süresi de “PW”
süresi kadar belirlenir.
Yarıiletken Elemanlar
Diyot:
D(isim)
NA NK
model ismi
biçiminde tanımlanır. NA anot ucu, NK ise katod ucunun bağlandığı düğümlerdir. Diyot modeli
Spice giriş dosyasında:
.MODEL
model ismi
D(diyot model parametreleri)
Bipolar Transistör (BJT):
Q(isim)
NC NB
NE
model ismi
biçiminde tanımlanır.
NC kolektör, NB baz ve NE emetör ucunun bağlandığı düğümlerdir. Transistör modeli :
.MODEL
model ismi
eleman tipi(NPN-PNP)(transistör model parametreleri)
MOS Transistör:
M(isim)
ND
NG
NS
NB
model ismi
L=…
W=…
ND drain, NG gate, NS source, NB bulk ucunun bağlandığı düğümleri gösterir. L kanal boyu,
W ise kanal genişliğidir.
.MODEL
model ismi
eleman tipi(NMOS-PMOS)(MOS transistör model parametreleri)
Analiz Komutları
DC Analiz:
.DC
başlangıç değer
son değer
adım
şeklinde tanımlanır. Bu durumda giriş işareti, belirlenen başlangıç değerinden son değere kadar
girilen adım aralıklarıyla tarama yapar. Her bir giriş gerilim değeri için devre analiz edilip
sonuçlar kaydedilmektedir. Devrenin DC transfer karakteristiğinin çıkartılmasında kullanılır.
67
AC Analiz:
lin
oct
nokta sayısı başlangıç değeri
son değer
dec
şeklinde tanımlanır. Bu analizde değişken frekanstır. Analiz, frekansın belirli bir aralıkta lineer
(lin) arttırılmasıyla yapılabileceği gibi oktav’lık (oct) veya dekat’lık (dec) artımlarla da
yürütülebilir. Lineer değişimlerde toplam nokta sayısı, oktav’lık veya dekat’lık değişimlerde ise
bir oktav veya dekat boyunca alınacak nokta sayısı verilir. AC tarama ile devrenin frekans cevabı
çıkartılabilir ya da empedansın frekansla değişimi incelenebilir.
. AC
Zaman Domeni Analizi
.TRAN
Tstep
Tstop
şeklinde tanımlanır. Zaman domeni analizi her zaman t = 0 dan başlar ve kullanıcının verdiği
adımlarla Tstop değerine kadar yapılır. Zaman domeni analizi ile devrelerin sinüsoidal ya da
darbe gibi giriş işaretlerine karşılık verdiği çıkışlar incelenebilir (örn. doğrultucu, kırpıcı,
kuvvetlendirici vb.)
NOT : Spice giriş dosyası her zaman ;
.END
ifadesiyle sonlandırılır..
Basit bir devrenin PSpice programının yazımı Şekil 2’de verilmiştir.
Example_1 EXMPL01.CIR
Vs 1 0 DC 20.0V
Ra 1 2 5.0k
Rb 2 0 4.0k
Rc 3 0 1.0k
Is 3 2 DC 2.0mA
.END
Şekil 2.
Bu deneyde Orcad PSpice programı kullanılarak elektrik devrelerinin simülasyonu
gösterilecektir. Bu programda görsel bir arayüz mevcuttur. Dolayısıyla herhangi bir giriş dosyası
oluşturmadan görsel olarak devre şematiği “Orcad Capture” ile çizilir ve “Orcad PSpice A/D” ile
simülasyonu gerçekleştirilir.
68
Deney Hakkında Genel Bilgiler:
Elektriksel işaretin frekans spektrumuna biçim vermekte kullanılan devreye filtre denir.
Filtrelerin elektronik ve haberleşme sistemlerinde çeşitli uygulamaları vardır. Bunlar, genellikle,
sisteme uygulanan frekanslardan sadece istenenlerin geçirilmesi amacıyla kullanılmaktadır.
Filtreler, kuvvetlendiriciler gibi çeşitli devrelerin; Sinüsoidal Sürekli Haldeki (SSH) devre
fonksiyonlarının H ( jω ) ve bu fonksiyonlara ilişkin Genlik-Frekans ve Faz-Frekans
karakteristiklerinin bilinmesi mühendislik açısından oldukça önemlidir. Çünkü bir devreye ilişkin
devre fonksiyonunun frekansa bağlı olarak genlik ve faz değişimleri biliniyorsa, bu durumda, o
devrenin girişine uygulanacak herhangi bir frekanstaki sinüsoidal işaretin, yine o devrenin
çıkışından hangi genlik ve fazda elde edileceği de biliniyor demektir.
Sonuç olarak, bu diyagramlara bakarak bir devrenin herhangi bir frekansta ne şekilde davrandığı;
yani bir kuvvetlendirme mi yoksa bir zayıflatma mı yaptığı; giriş işaretinin fazını çıkışta kaç
derece değiştirdiği, kolaylıkla anlaşılabilir. Bir devreye ilişkin devre fonksiyonu incelenirken,
frekans yanıtının geniş bir frekans aralığında (1Hz-1Ghz) incelenmesi gerekir. Faz ve genlik
(kazanç) yanıtının oldukça geniş bir aralığı (0-106) kapsaması nedeniyle, devre fonksiyonlarına
ilişkin diyagramların lineer ölçek kullanarak çizilmesi yerine logaritmik ölçek kullanarak
çizilmesi daha uygundur. Böylelikle geniş aralıkları kapsayan diyagramlar; küçük boyuttaki
koordinat sistemleri içine sığdırılır. Logaritmik-genlik ve faz açısının, logaritmik-frekansa (log f)
veya logaritmik açısal-frekansa (log ω ) bağlı olarak değişimlerini gösteren diyagramlar ilk kez
H.W.Bode tarafından sunulmuştur.
Transfer fonksiyonu H(s) olan bir devre u (t ) = sin(ωt ) sinüsoidal fonksiyonu ile uyarılırsa
sürekli hal çıkışı y(t);
y (t ) =| H ( jω ) | sin[ωt + φ (ω )]
biçiminde olacaktır. Burada | H ( jω ) | ve φ (ω ) sırasıyla transfer fonksiyonunun genlik ve fazını
göstermektedir. Bode diyagramlarında | H ( jω ) | ’nın logaritmik genlik değeri;
| H ( jω ) | dB = 20 log10 | H ( jω ) | dB olarak tanımlanır ve birimi decibeldir(dB).
| H ( jω ) | −ω eğrisinin biçimine göre filtreler şu temel gruplara ayrılır: alçak geçiren, yüksek
geçiren, band geçiren, band söndüren ve tüm geçiren.
Band geçiren pasif filtre devresi Şekil 1’de verilmiştir.
|H(jω)|
1
ω
Şekil 1.
ω0
Şekil 2.
69
Şekil 1’deki devrede 1. düğüme K.A.Y uygulanarak v2 ( t ) için integro-diferansiyel denklem
aşağıdaki şekilde verilebilir:
dv ( t ) 1 t
1
v ( t ) − v2 ( t )  = C 2 + ∫ v2 ( t ) dt

R
dt
L 0
Burada ilk koşul iL ( 0 ) = 0 olarak alınmıştır. Laplace dönüşümü uygulanırsa şu sonuç elde edilir:
1
1
1
V ( s ) − V2 ( s ) = CsV2 ( s ) + V2 ( s )
R
R
Ls
Buradan ise aşağıdaki transfer fonksiyonu ifadesi elde edilir:
1
s
V2 ( s )
RC
H (s) =
=
V ( s ) s2 + 1 s + 1
RC
LC
Tanım olarak aşağıdaki ifadeler verilirse:
1
C
,Q=R
ω0 =
L
LC
Burada, ω o : Merkez Frekansı, Q : Kalite Faktörü
Yukarıdaki transfer fonksiyonu ifadesi
ω0
H (s) =
Q
s2 +
ω0
s
s + ω0 2
Q
haline gelir. Sinüzoidal sürekli hal için genlik ifadesi;
H ( jω ) =
1
12
2

ω0  
2 ω
1 + Q  −  

 ω0 ω  
şeklindedir. H ( jω ) ’nın açısal frekansa göre grafiği Şekil 2’de verilmiştir. Q >> 1 için
bantgenişliği şu ifadeyle verilebilir; ∆ω = ω2 − ω1 =
ω
1
= 0
RC Q
70
Fourier Analizi:
v ( t ) periyodik bir dalga şekli olmak üzere şu şekilde Fourier serisine açılabilir:
∞
v ( t ) = V0 + ∑ Vn cos ( nω0t + φn )
n =1
Buradaki sembollerin anlamı aşağıda verilmiştir.
V0 : v ( t ) ’nin DC değeri;
Vn : n. harmoniğin genliği (birinci harmonik temel olarak da adlandırılır.);
nf 0 , nω0 : n. harmoniğin frekansıdır. f 0 temel frekans, ω0 ise temel açısal frekans olup
1
2π
f0 =
, ω0 =
T0
T0
ile hesaplanır. Burada T0 temel periyot, başka bir deyişle v ( t ) ’nin periyodudur.
Deney Öncesi Hazırlıklar:
Deneyde bulunması istenilen değerleri verilen teorik bilgiden yararlanarak hesaplayınız.
Deney Öncesi Hazırlık Raporunda Đstenenler:
1. Deney öncesi hazırlıklar bölümündeki istenenleri sırasıyla bulunuz ve düzenli bir şekilde
raporunuza yazınız.
2. ORCAD 16.3 programını kullanarak deneyde gerçekleştireceğiniz bütün devrelerin
simülasyonunu yapınız ve elde ettiğiniz simülasyon sonuçlarını grafiksel olarak
raporunuza ekleyiniz ve sonuçları yorumlayınız.
Deney Sırasında Yapılacaklar:
1. a) Şekil 3 ile verilen devreyi “ORCAD Capture” programı ile oluşturunuz. Devrenin
birim basamak cevabını elde etmek için girişe uygulanması gereken birim basamak
fonksiyonunu(u(t)), darbe kaynağı “VPulse” elemanını kullanarak elde ediniz. Devrenin
zaman domeninde analizi gerçekleştirilecektir. Bunun için analiz türü olarak “Time
domain(Transient)” seçiniz. vc ( t ) çıkış gerilimi ve ic ( t ) akımını zamana göre 10 saniye
boyunca çizdiriniz( R = 1 kΩ ve C = 1 mF alınacaktır). Kapasite elemanının R direnci
üzerinden dolmasını baz alarak grafikler hakkında yorum yapınız.
Şekil 3.
b) Şekil 3’teki devrede “VPulse” kaynağı yerine “VAC” elemanı bağlayınız. Analiz türü
olarak “AC Analiz” seçiniz. AC kaynağın tepe değeri 1V , frekans analiz aralığı 10Hz ile
1GHz arası olacaktır. Simülasyonu gerçekleyiniz ve elde edilen frekans karakteristiğini
yorumlayınız. ωc köşe frekansını grafik üzerinden bulunuz.
71
2. 1. adımda yapılanları çıkış gerilimini direnç üzerinden alarak tekrarlayınız.
3. Şekil 1’de verilen filtre devresini “ORCAD Capture” programında oluşturunuz. Giriş
gerilimini Şekil 4’teki grafikte gösterildiği şekilde kare dalga olarak alınız. Bunun için
darbe kaynağı “VPulse” elemanını kullanınız. Bu dalga şeklinin sadece temel harmoniğini
geçiren bir filtre devresi tasarlanacaktır.
Şekil 4.
a) Bu filtre için merkez frekansı f 0 ve ω0 ’ı bulunuz. L = 1 mH alarak C ’yi
hesaplayınız.
b) Q = 10 olması için R değerini hesaplayınız. Filtrenin bant genişliğini
hesaplayınız.
c) | V2 ( jω ) |’nın frekansa göre grafiğini elde etmek için AC analiz yapınız.
| V2 ( jω ) |’yı frekansa göre çizdiriniz(Lineer ve logaritmik ölçekler kullanınız). Bu
grafikten merkez frekansını ve bantgenişliğini ölçünüz ve a ve b’de hesapladığınız
değerlerle karşılaştırınız.
d) “ORCAD Capture” programını kullanarak aynı devre için ve tekrar Şekil 4’teki
dalga şekli giriş olarak alınarak zaman domeninde analiz yapınız. v2 ( t ) ne tür bir
dalga şekline sahiptir? v2 ( t ) ’nin grafiğine bakarak frekansını hesaplayınız. Neden
saf sinüzoidal bir dalga şekli olmadığı hakkında yorum yapınız.
e) “Orcad PSpice A/D” programının Fourier özelliğini kullanarak v1 ( t ) ve v2 ( t ) ’nin
frekans spektrumlarını elde ediniz. Bu frekans spektrumlarının grafiklerini
çizdirerek karşılaştırınız ve bunun sonucunda yapılan filtreleme işlemi hakkında
yorum yapınız. v2 ( t ) ’nin spektrumunu kullanarak neden saf sinüzoidal bir dalga
şekli olmadığını açıklayınız.
f) (b-e) arasını Q = 20 için tekrar ediniz. Elde ettiğiniz sonuçları Q = 10 için elde
edilenlerle karşılaştırınız.
4. Şekil 5 ile verilen devreyi “ORCAD Capture” programında oluşturunuz ve giriş
gerilimini Şekil 4’teki grafikte gösterildiği gibi kare dalga olarak alınız. Bu dalga
şeklinin sadece temel harmoniğini geçiren bir filtre devresi tasarlanacaktır.
a) Bu filtre için merkez frekansı f 0 ve ω0 ’ı bulunuz. Filtrenin kalite faktörünün
Q = 10 olması istenmektedir. Aşağıda verilen eşitlikleri kullanarak devrenin eleman
değerlerini bulunuz.
72
R1 =
Q
,
ω0 C
R2 =
Q
2
(2Q -1)ω0 C
,
R3 =
2Q
ω0 C
burada C1 = C2 = C’dir.
b) | V2 ( jω ) |’nın frekansa göre grafiğini elde etmek için AC analiz yapınız. | V2 ( jω ) |’yı
frekansa göre çizdiriniz.(Lineer ve logaritmik ölçekler kullanınız.)Bu grafikten
merkez frekansını ve bantgenişliğini ölçünüz ve a ve b’de hesapladığınız değerlerle
karşılaştırınız.
Şekil 5.
c) “ORCAD Capture” programını kullanarak aynı devre için ve tekrar Şekil 4’teki
dalga şekli giriş olarak alınarak zaman domeninde analiz yapınız. v2 ( t ) ne tür bir
dalga şekline sahiptir? v2 ( t ) ’nin grafiğine bakarak frekansını hesaplayınız. Neden
saf sinüzoidal bir dalga şekli olmadığı hakkında yorum yapınız.
d) “Orcad PSpice A/D” programının Fourier özelliğini kullanarak v1 ( t ) ve v2 ( t ) ’nin
frekans spektrumlarını elde ediniz. Bu frekans spektrumlarının grafiklerini
çizdirerek karşılaştırınız ve bunun sonucunda yapılan filtreleme işlemi hakkında
yorum yapınız. v2 ( t ) ’nin spektrumunu kullanarak neden saf sinüzoidal bir dalga
şekli olmadığını açıklayınız.
KAYNAKLAR:
[1]. Nilsson J.W., Riedel S.A., “Introduction to PSpice Manual Electric Circuits Using Orcad
Release 9.2”, Prentice Hall 2002
[2]. Rashid M.H.,”SPICE for Circuits and Electronics Using Pspice”, Prentice Hall, 1995.
[3]. http://bwrc.eecs.berkeley.edu/Classes/IcBook/SPICE/