"22
ENDÜSTR!YEL ELEKTRON!K
T =
R1 C 1
.V H
V CC - V BE
(4."4)
olur. Burada, VH büyüklü#ü Schmitt tetikleme devresinin histerezis geni$li#ini
göstermektedir. Osilasyon frekansı da f = "/T olur.
4.2. !"lemsel geçi" iletkenli#i kuvvetlendiricisi, OTA
+V
T
+
IB
T6
5
T
1
T
T7
T8
CC
2
V IN
-
+VO
R T3
T4
T9
T 10
-V EE
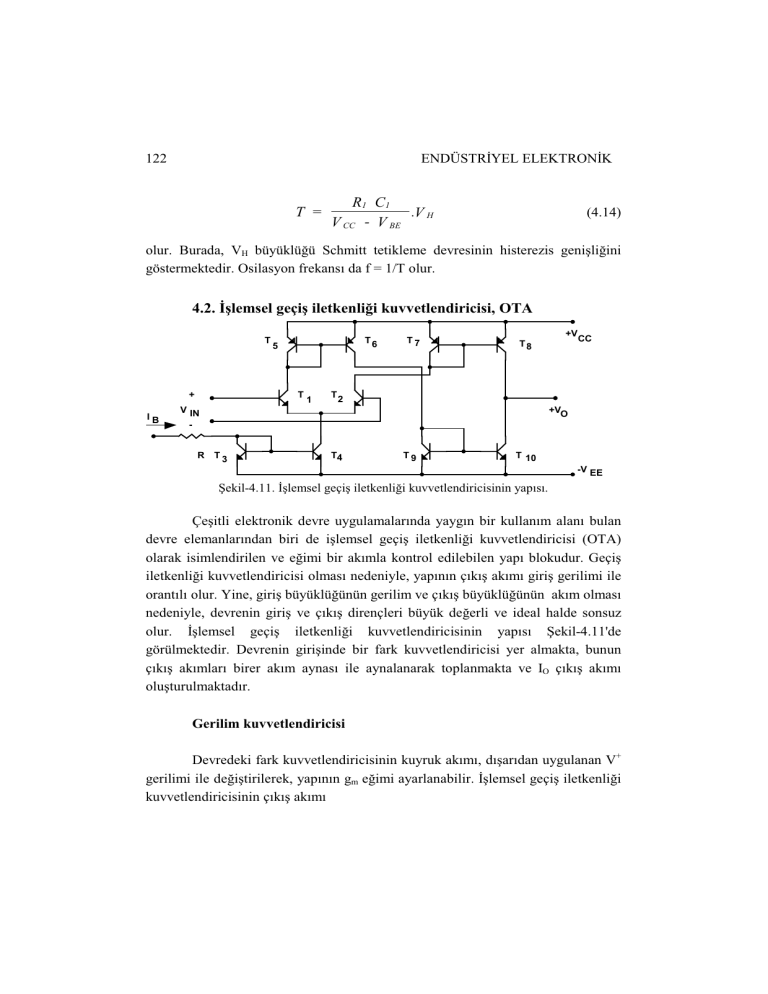
%ekil-4."". !$lemsel geçi$ iletkenli#i kuvvetlendiricisinin yapısı.
Çe$itli elektronik devre uygulamalarında yaygın bir kullanım alanı bulan
devre elemanlarından biri de i$lemsel geçi$ iletkenli#i kuvvetlendiricisi (OTA)
olarak isimlendirilen ve e#imi bir akımla kontrol edilebilen yapı blokudur. Geçi$
iletkenli#i kuvvetlendiricisi olması nedeniyle, yapının çıkı$ akımı giri$ gerilimi ile
orantılı olur. Yine, giri$ büyüklü#ünün gerilim ve çıkı$ büyüklü#ünün akım olması
nedeniyle, devrenin giri$ ve çıkı$ dirençleri büyük de#erli ve ideal halde sonsuz
olur. !$lemsel geçi$ iletkenli#i kuvvetlendiricisinin yapısı %ekil-4.""'de
görülmektedir. Devrenin giri$inde bir fark kuvvetlendiricisi yer almakta, bunun
çıkı$ akımları birer akım aynası ile aynalanarak toplanmakta ve IO çıkı$ akımı
olu$turulmaktadır.
Gerilim kuvvetlendiricisi
Devredeki fark kuvvetlendiricisinin kuyruk akımı, dı$arıdan uygulanan V+
gerilimi ile de#i$tirilerek, yapının gm e#imi ayarlanabilir. !$lemsel geçi$ iletkenli#i
kuvvetlendiricisinin çıkı$ akımı
ANALOG TÜMDEVRE UYGULAMALARI
"23
R2
R1
+
+V I
R
+V O
RL
3
R
B
+V
%ekil-4."2. !$lemsel geçi$ iletkenli#i kuvvetlendiricisi ile kurulan gerilim kuvvetlendiricisi
devresi.
I O = g mV I
(4."5)
ve geçi$ iletkenli#i de
gm =
IB
2V T
(4."6)
olur. Daha önce de belirtildi#i gibi, IB kuyruk akımı, devreye dı$arıdan ba#lanan R
direnci üzerinden uygulanan V+ gerilimi ile yararlanabilir. Kuvvetlendiriciye
dı$arıdan ba#lanacak RL yük direnci RL << rO olmalı, ba$ka bir deyi$le
kuvvetlendiricinin çıkı$ direncinden yeteri kadar küçük olmalıdır.
Kuvvetlendiricinin açık çevrim kazancı
KV =
I B RL
vo
= gm R L =
2V T
vi
(4."7)
ba#ıntısıyla hesaplanabilir. (4."7) ba#ıntısından fark edilebilece#i gibi,
kuvvetlendiricinin kazancı IB kutuplama akımı ile orantılıdır.
!$lemsel geçi$ iletkenli#i kuvvetlendiricilerinin ba$lıca uygulama alanları
arasında gerilim yahut akım kontrollu kuvvetlendiricilerin, örnekleme-tutma
devrelerinin, ço#ullayıcı devrelerin, analog çarpma devrelerinin, aktif süzgeçlerin
gerçekle$tirilmesi yer almaktadır. Bu uygulama devrelerinden bazı örnekler
a$a#ıda verilmi$tir.
"24
ENDÜSTR!YEL ELEKTRON!K
!$lemsel geçi$ iletkenli#i kuvvetlendiricisi ile kurulan bir gerilim
kuvvetlendiricisi yapısı %ekil-4."2'de verilmi$tir. Devre, i$lemsel kuvvetlendirici
ile kurulan faz döndüren kuvvetlendirici yapısının e$de#eridir. Tasarlanacak
kuvvetlendirici için RL yük direnci ve geribeslemeli durumdaki KVf gerilim kazancı
bellidir. Yapının KVO açık çevrim kazancı, geribeslemeli durumdaki kazançtan en
az "0 defa daha büyük olmalıdır. Ba$ka bir deyi$le
KVO ≥ 10 KVf
$artı sa#lanmalıdır. Bu $artdan hareket edilirse, gm = KVO/RL ba#ıntısı yardımıyla
kuvvetlendiricinin e#imi ve (4."6) ba#ıntısı kullanılarak da IB kutuplama akımı
belirlenebilir. Bu akımı sa#layan kutuplama direnci de
RB =
V CC - V B
IB
(4."8)
olur. Kurulan faz döndüren kuvvetlendiricinin sa#ladı#ı gerilim kazancı KVf = R2/R" olur. yine, devrede R2 >> RL olmalıdır.
Ço#ullayıcı
!$lemsel geçi$ iletkenli#i kuvvetlendiricileri yardımıyla ço#ullayıcı devresi
gerçekle$tirmek mümkündür. Üç kanallı bir ço#ullayıcı devresi %ekil-4."3'de
verilmi$tir. Yapı üç geçi$ iletkenli#i kuvvetlendiricisi ve bir MOSFET ile
kurulmu$tur. Geçi$ iletkenli#i kuvvetlendiricilerinin yüksek empedanslı çıkı$ları
paralel ba#lanmı$tır. Kuvvetlendiricilerin kutuplama giri$lerine birer RT direnci
üzerinden tarama i$aretleri uygulanır. !lgili tarama i$aretinin yüksek seviyeye
getirilmesiyle kuvvetlendiricilerden biri seçilmi$ olur ve aktif hale gelir. Bu
durumda, o kuvvetlendiricinin giri$ine uygulanan gerilim ortak çıkı$ noktasına
aktarılmı$ olur. Devredeki MOS tranzistor ayırıcı kat olarak görev yapar. MOS
tranzistorun kaynak ucundan her bir kuvvetlendiricinin faz döndüren giri$ine
geribesleme uygulanmı$tır. Kuvvetlendiricilerden birinin seçilmesi durumunda,
sistem geribeslemeli ve birim kazançlı bir kuvvetlendirici olarak çalı$ır. Yapıyı
daha de#i$ik bir biçimde kurarak kazançlı kuvvetlendirici elde etmek de
ANALOG TÜMDEVRE UYGULAMALARI
"25
mümkündür. Bu durumda, sisteme uygulanacak geribeslemenin negatif
geribesleme olabilmesi için, geribesleme i$aretinin kuvvetlendiricilerin uygun
fazdaki giri$lerine verilmesi gerekece#i açıktır.
R1
+V
CC
+
+V 1
R2
RT
T
R1
1
+
+V
2
T
R2
RT
T2
+V O
R1
+
+V 3
R2
RT
R
T3
%ekil-4."3. Üç kanallı ço#ullayıcı devresi.
Geçi" iletkenli#i kuvvetlendiricisi ile analog çarpma devresi gerçekle"tirilmesi
!$lemsel geçi$ iletkenli#i kuvvetlendiricisinin e#iminin akımla kontrol
edilebilmesi özelli#inden yararlanarak, analog çarpma devresi i$levi kolaylıkla
sa#lanabilir. Üç geçi$ iletkenli#i kuvvetlendiricisi ile kurulan bir analog çarpma
devresi yapısı %ekil-4."4'de verilmi$tir.
Devrede OTA" ve OTA2 geçi$ iletkenli#i kuvvetlendiricilerinin çıkı$ları
paralel ba#lanmı$tır. OTA"'in faz döndüren giri$i ise OTA2'nin faz döndürmeyen
giri$ine ba#lıdır ve buraya VX giri$ gerilimi uygulanmı$tır. OTA3 geçi$ iletkenli#i
kuvvetlendiricisi faz döndüren kuvvetlendirici olarak çalı$tırılmaktadır. Bu
kuvvetlendiricinin giri$ine ve OTA2'nin akım kontrol giri$ine VY giri$ gerilimi
uygulanmaktadır. OTA3'ün çıkı$ gerilimi ise OTA"'in kontrol gerilimini olu$turur.
Buna göre, OTA" ve OTA2 geçi$ iletkenli#i kuvvetlendiricilerinin çıkı$ akımları
"26
ENDÜSTR!YEL ELEKTRON!K
OTA"
+V X
I O1
+
R1
+V Y
+V O
RL
OTA2
I O2
+
R
1
R
RF
F
+
OTA3
%ekil-4."4. !$lemsel geçi$ iletkenli#i kuvvetlendiricileri ile analog çarpma devresi
gerçekle$tirilmesi.
I O" = - g m"V X
, I O2 = g m2 V X
olacaktır. Kuvvetlendiricilerin çıkı$ empedansları yüksek oldu#undan, bunların
çıkı$ akımları toplanır. Öte yandan kuvvetlendiricilerin e#imleri kutuplama
akımları ile orantılıdır. OTA"'in kutuplama akımı -VY ile, OTA2'nin kutuplama
akımı ise VY ile orantılı olur. Devrenin çıkı$ gerilimi
VO = V X . R L .[ g m2 − g m" ]
olur. IB2 kutuplama akımı
I B2 =
ba#ıntısıyla belirlenir.
VY − ( −VEE )
R1
ANALOG TÜMDEVRE UYGULAMALARI
k =
"27
1
2 V T R2
$eklinde bir büyüklü#ün tanımlanmasıyla OTA" ve OTA2'nin geçi$ iletkenlikleri
g m" = k .[ −VY − ( −VEE )]
g m2 = k .[VY − ( −VEE )]
biçiminde ifade edilebilir. Bu büyüklüklerin çıkı$ gerilimini veren ba#ıntıda
yerlerine konmasıyla
V O = k R L V X {[-V EE + V Y ] - [-V EE - V Y ]}
V O = 2k R L V X V Y
(4."9)
elde edilir. Devre dört bölgeli analog çarpma devresi olarak çalı$ır.
OTA-C aktif süzgeçleri
!$lemsel kuvvetlendiricilerden daha geni$ bandlı olmaları ve e#imlerinin
kontrol edilebilir olması nedeniyle OTA'lar da gittikçe yaygınla$arak kullanım
alanı bulmaktadır. Yine, CMOS teknolojisi ile kolayca tümle$tirilebilmeleri
nedeniyle, OTA-C aktif süzgeçleri de yaygınla$makta ve bu alanda gerek OTA
gerekse aktif süzgeç gerçekle$tirilmesi için yeni devre topolojileri önerilmektedir.
Aktif süzgeç yapılarında kullanılmaya elveri$li OTA yapıları piyasada
bulunmakta (CA 3080 vb), geni$ bandlı olmaları, e#imlerinin IA kutuplama akımı
ile kontrol edilebilmesi, yapılarının tümle$tirmeye uygun ve basit olması gibi
nedenlerden dolayı yaygın bir kullanım alanı bulmakta, OTA-C süzgeç yapılarının
yanısıra, analog çarpma devreleri ve yüksek frekans osilatörlerinin
gerçekle$tirilmesi amacıyla da bu devre yapılarından yararlanılmaktadır.
Bu amaca yönelik çe$itli çalı$malarda, minimum sayıda OTA ve bir ucu
topraklanmı$
kondansatörlerle
kurulan
bikuadratik
aktif
süzgeçler
gerçekle$tirilmesi için devre sentezi yöntemleri önerilmi$tir. Bilindi#i gibi,
bikuadratik genel transfer fonksiyonu
"28
ENDÜSTR!YEL ELEKTRON!K
a 2 s2 + a1 s + a0
G(s) =
s2 + b1 s + b0
(4.20)
biçimindedir. Bu transfer fonksiyonunu sa#layan genel devre yapısı %ekil-4."5'de
verilmi$tir.
VI
OTA5
OTA6
+
-
+
OTA3
+
-
OTA1
OTA2
+
-
+
-
+
VO
OTA4
C1
C2
%ekil-4."5. !kinci dereceden transfer fonksiyonunu gerçekleyen genel OTA-C aktif süzgeç
yapısı.
Bu devrede tasarım e$itlikleri
gm1
C1
gm 2
C2
gm 3
g m4
gm 5
C1
gm6
C2
b0
b1
b1
=
a2
=
= a2
a0
b1
a1
=
a2
=
(4.2")
ANALOG TÜMDEVRE UYGULAMALARI
"29
Tablo-4.". %ekil-4."6’daki süzgeçlerin transfer fonksiyonları ve eleman ba#ıntıları
Süzgeç
Transfer
fonksiyonu
Eleman de#erleri
$ekil-4.%6a
Alçak
geçiren
$ekil-4.%6b
Alçak
geçiren
$ekil-4.%6c
Band
geçiren
$ekil-4.%6d
Yüksek
geçiren
$ekil-4.%6e
Band
geçiren
a0
s + b" s + b0
gm" b0
=
C"
b"
g m2
= b"
C2
a0
s + b" s + b0
a 0 = b0 ,
gm" b0
=
,
C"
b"
a" s
s + b" s + b0
gm" b0
=
C"
b"
g m2
= b"
C2
g m3
= a"
C2
a2 s2
s 2 + b" s + b0
gm" b0
=
C"
b"
g m3
= a2
g m4
g m2 b"
=
C2
a2
a" s + a 0
s + b" s + b0
gm2
= b"
C2
g m3 a 0
=
,
C"
b"
$ekil-4.%6.f
Band
geçiren
a" s + a 0
s + b" s + b0
gm2
= b"
C2
a" =
$ekil-4.%6g
Band
söndüren
a2 s 2 + a0
s 2 + b" s + b0
g m2 b"
=
C2
a2
a 0 = b0 ,
$ekil-4.%6h
Band
söndüren
a2 s 2 + a0
s 2 + b" s + b0
g m2 b"
=
C2
a2
gm5 a0
=
C" b"
$ekil-4.%6i
Tümgeçiren
s 2 − b" s + b0
s 2 + b" s + b0
gm" b0
=
C"
b"
g m4
= a"
C2
gm" b0
=
C"
b"
a 0 = b0
gm" b0
=
C"
b"
gm3
= a2
gm 4
gm" b0
=
C"
b"
gm3
= a2
gm 4
gm" b0
=
,
C"
b"
gm3
="
g m4
g m2 b"
=
,
C2
a2
g m5
= b" ,
C2
2
2
2
2
2
gm3 a0
=
C" b"
g m2
= b"
C2
b0
,
b"
"30
biçimindedir. Bu
göstermektedir.
ENDÜSTR!YEL ELEKTRON!K
ba#ıntılarda
gmi
büyüklükleri
i.ci
OTA'nın
e#imini
%ekil-4."5'deki genel yapıya dayanan ve minimum sayıda OTA içeren
çe$itli tipten ikinci derece aktif OTA-C süzgeci yapıları %ekil-4."6'da
gösterilmi$tir. Bu süzgeç yapılarına ili$kin transfer fonksiyonları ve tasarım
büyüklükleri de Tablo-4."’de belirtilmi$tir.
OTA-C osilatörleri
Sadece geçi$ iletkenli#i kuvvetlendiricisi ve kondansatörler kullanılarak
gerçekle$tirilen osilatör yapiları yüksek frekans devrelerinde oldukça fazla yarar
sa#larlar. Devrelerin sa#ladı#ı en büyük yarar, yapıda endüktans bulunmaması,
OTA nın açık çevrimde çalı$abilmesi, ba$ka
bir deyi$le, yapılan yerel
geribeslemelerle frekans cevabına ili$kin kutuplar için ek bir sınırlama
getirmemesidir. OTA nın e#iminin bir tasarım parametresi olarak kullanılması da
elde edilen di#er bir yarar olarak de#erlendirilebilir. Bu e#im akımın bir
fonksiyonu oldu#undan OTA nın kuyruk akımının de#i$tirilmesiyle söz konusu
parametre ve bununla da frekansı de#i$tirme olana#ı bulunmaktadir. Devrenin
çalı$ması ikinci dereceden bir osilatör devresinin karakteristik denkleminin elde
edilmesine dayanır. Bu karakteristik denklem
s2 - b.s + Ω2O = 0
$eklindedir. b ve Ω0 büyüklükleri OTA’ların geçi$ iletkenliklerinin ve kapasitelerin
fonksiyonudur. Bu karakteristik denklem çe$itli yapı düzenleriyle sa#lanabilir. Bu
düzenlerden 2OTA3C (iki OTA ve üç kapasite ile kurulan düzen), 3OTA2C,
4OTA2CI, 4OTA2CII ve 4OTA4C düzenleri %ekil-4."7'de verilmi$tir. Bu yapılara
ili$kin karakteristik büyüklükler de Tablo-4.2’de gösterilmi$tir.