fizik2 uygulama soruları bölüm 26

DÖNEM:2005-2
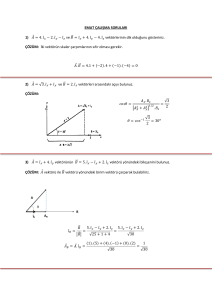
FİZİK2 UYGULAMA SORULARI
BÖLÜM 26
a
1- Dört kondansatörden oluşan köprü
devresi şekildeki gibi Vc-Vd=V0 potansiyel
farkında tutulmaktadır. Devredeki C1
değişken kondansatörü a, b noktaları
arasındaki potansiyel farkını sıfır yapacak
şekilde ayarlanır. Eğer C1=9µF , C2=18µF ve
C3=6µF ise bilinmeyen Cx kondansatörünün
sığası nedir?
C1
Cx
c
d
C2
C3
b
Cx=3µF
2- Paralel plakalı bir kondansatörün plaka alanı 400cm2 ve plaka uzaklığı 0.5 cm
dir. Plakalar arasındaki potansiyel farkı 1500 V tur.
a) Plakalar arasındaki elektrik alanı bulunuz.
b) Her bir plaka üzerindeki yük ne kadardır?
c) Plakaların biri üzerine uygulanan kuvveti bulunuz.
d) Plakalar arasındaki uzaklık yüzde 20 arttırıldığında depolanan enerji
miktardaki değişiklik ne kadar olur? Bu sonuç c) şıkkının cevabı ile
tutarlımıdır?
a) 3.105 V/m
b) 1.06 10-7 C
c) 1.59 10-2 N
3- Çok uzun bir silindirik kondansatör
şekildeki gibi eş merkezli dört silindirden
oluşturulmuştur. Silindirlerin yarıçapları
merkezden itibaren sırasıyla RA, RB, RC ve
RD dir. RB ve RC yarıçaplı silindirler iletken
telle birbirine bağlanmıştır. Bu uzun silindirik
kondansatörün birim uzunluk başına sığasını
bulunuz.
C
=
L
2πε 0
⎛ RB RD
ln⎜⎜
⎝ RA RC
d) 1.59 10-5 J
RD
RC
RB
RA
⎞
⎟
⎟
⎠
4- Sığası C olan iki özdeş paralel plakalı
kondansatör Va-Vb=V toplam potansiyeli
κ
b
a
altında seri olarak bağlanmıştır. Sabiti κ
olan dielektrik bir madde bu kondansatörlerden birini dolduracak şekilde kondansatöre
yavaşça yerleştiriliyor. Kondansatörlerin toplam
potansiyel enerjisinde, her bir kondansatörün yükünde ve potansiyel düşüşünde
meydana gelen değişimi bulunuz.
∆U =
κ −1
CV 2
4(κ + 1)
∆Q1 = ∆Q2 =
κ −1
CV
4(κ + 1)
∆V1 =
1−κ
V
2(κ + 1)
∆V2 =
κ −1
V
2(κ + 1)
5- Bir kondansatör kenar uzunluğu L ve plaka aralığı d olan iki kare plakadan
yapılmıştır. Şekildeki gibi dielektrik
L
sabiti κ olan bir madde, kondansatör
içine x kadar sokulmuştur.
κ
d
x
x=0
a) Kondansatörün eşdeğer sığasını bulunuz.
b) Plakalar arasındaki potansiyel farkı ∆V=V0 ise kondansatörde depolanan
enerjiyi bulunuz.
c) ∆V potansiyel farkının sabit olduğunu varsayarak, dielektrik madde üzerine
etki eden kuvvetin yön ve büyüklüğünü bulunuz.
d) Kondansatörün dielektrik üzerine yaptığı işi bularak c) şıkkı ile karşılaştırınız.
e) Bu örnekte, kondansatör dielektrik maddeyi içine doğru çekmek ister. Sizce
dielektrik üzerindeki net kuvvetin yatay doğrultuda çıkmasının nedeni ne
olabilir?
a) Ceş =
ε 0 L2 ⎡
x
⎤
1 + (κ − 1) ⎥
d ⎢⎣ L
⎦
b) U =
V02ε 0 L2
2d
x
⎤
⎡
⎢1 + L (κ − 1) ⎥
⎦
⎣
6- Şekildeki gibi paralel plakalı bir
kondansatörün bir plakası düşeyle
çok küçük açı yapacak şekilde
eğiltilmiştir. Plakalar kare olup
yüzey alanları A dır. Bu kondansatörün
sığasının θ çok küçük açı değeri için
C=
ε0 A ⎡
⎢1 −
d ⎢⎣
θ A⎤
⎥
d ⎥⎦
1
ln(1 + x ) ≅ x − x 2
2
ile verilebileceğini gösteriniz.
c) F =
ε 0 LV02
2d
(κ − 1)
Sola doğru
L
θ
d