PARABOL

PARABOL
2
Bu bölümde birinci dereceden fonksiyon y=f(x)=ax+b ve ikinci dereceden fonksiyon y=f(x)=ax +bx+c grafiklerini yüzeysel ola2
rak inceleyeceğiz. f(x)=ax +bx+c ikinci dereceden bir bilinmeyenli polinom fonksiyonun grafiği konunun ilerleyen bölümlerinde
detaylı olarak incelenecektir.
çözüm
kavrama sorusu
y=f(x)=2x – 6
x değişkenine farklı değerler vererek y değerlerini bulup grafiği çizeriz.
fonksiyonunun grafiğini çiziniz.
Birinci dereceden fonksiyonların grafiğini çizmek için
bu fonksiyonların geçtiği iki noktayı bilmek yeterlidir.
x=0 için y=f(0)=2.0 – 6=– 6 , (0, – 6)
x=3 için y=f(3)=2.3 – 6=0
, (3, 0)
Bulduğumuz (0, – 6) ve (3, 0) noktalarından geçen doğru
dik koordinat sisteminde çizilir.
çözüm
kavrama sorusu
x değişkenine farklı değerler vererek y değerlerini bularak grafiği çizelim.
Aşağıdaki fonksiyonların grafiğini çiziniz.
2
a) y=f(x)=x
2
a) x=– 1 için y=f(– 1)=(– 1) =1 , (– 1, 1)
2
b) y=f(x)=– 2x
İkinci dereceden fonksiyonların grafiğini çizmek için
bu fonksiyonların geçtiği iki noktadan daha fazla bilgi gereklidir.
x=0
x=1
2
, (0, 0)
2
, (1, 1)
için y=f(0)=0 =0
için y=f(1)=1 =1
Bulduğumuz (– 1, 1) , (0, 0) ve (1, 1) noktalarından geçen eğri dik koordinat sisteminde çizilir.
2
a) x=– 1 için y=f(– 1)=(– 2)(– 1) =– 2 , (– 1, – 2)
x=0
x=1
2
, (0, 0)
2
, (1, – 2)
için y=f(0)=(– 2).0 =0
için y=f(1)=(– 2).1 =– 2
Bulduğumuz (– 1, – 2), (0, 0) ve (1, – 2) noktalarından geçen
eğri dik koordinat sisteminde çizilir.
4
Parabol
soru 1
soru 3
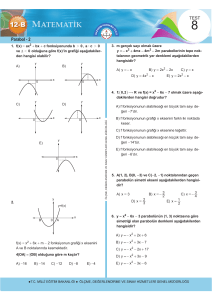
y=f(x)=2x – 4
y=f(x)=3x
fonksiyonunun grafiği aşağıdakilerden hangisidir?
2
fonksiyonunun grafiği aşağıdakilerden hangisidir?
soru 2
KARTEZYEN EĞİTİM YAYINLARI
y=f(x)=– 4x
fonksiyonunun grafiği aşağıdakilerden hangisidir?
2
y=f(x)=4 – x
fonksiyonunun grafiği aşağıdakilerden hangisidir?
soru 4
1 – A
2 – B
3 – C
5
4 – B
Parabol
İkinci Dereceden Fonksiyonlar
2
a, b, c reel sayı ve a ≠ 0 olmak üzere, f(x)=ax +bx+c fonksiyonuna ikinci dereceden bir bilinmeyenli fonksiyon, ikinci dereceden
fonksiyonun grafiğine ise parabol denir.
çözüm
kavrama sorusu
3
n – 2
f(x)=(m – 3)x +x
2
– 4x+5
f(x)=ax +bx+c biçiminde bir fonksiyon olmalıdır. Buna göre,
x'in en büyük kuvvetinin 2 olması gerekir.
fonksiyonu ikinci dereceden fonksiyon olduğuna göre, m+n
toplamı kaçtır, bulunuz.
O halde, m – 3=0 ve n – 2=2 dir.
m – 3=0 için m=3
n – 2=2 için n=4
m+n=3+4=7
Cevap: 7
çözüm
kavrama sorusu
2
f(x) = xm
-7
f(x) fonksiyonunun grafiği parabol olduğuna göre, f(x) ikinci
2
dereceden fonksiyon olmalıdır. O halde, m – 7=2 dir.
- 4x + 3
fonksiyonunun grafiği parabol olduğuna göre, m'nin alabileceği değerleri bulunuz.
2
2
m – 7=2 ise m =9 dur.
m =9 için m= – 3 veya m=3 dür.
2
Cevap: – 3 veya 3
çözüm
kavrama sorusu
2
f(x) = (m - 2)xm
-2
f(x) fonksiyonunun grafiği parabol olduğuna göre, f(x) ikinci
dereceden fonksiyon olmalıdır. O halde,
+ 5x - 2
fonksiyonunun grafiği parabol olduğuna göre, m kaçtır, bulunuz.
m – 2 ≠ 0 ve m – 2=2 olmalıdır.
m – 2 ≠ 0 için
2
m≠ 2 dir.
2
m – 2 = 2 için m =4 ,
m=– 2 veya m=2 dir.
m ≠ 2 olduğu için m=– 2 dir.
Cevap: – 2
çözüm
kavrama sorusu
2
Aşağıdaki fonksiyonların kaç tanesinin grafiği paraboldür,
bulunuz.
2
I)
f(x)=x +5x – 1
2
II)f(x)=– 2x +5x
3
2
V)f(x)=x – x +2
I, II, III, VI, ve VIII fonksiyonlarının grafiği paraboldür.
1 2
VI)f(x)= x – 2
2
IV, V ve VII parabol değildir.
III)f(x)=– x
x 2 + 4x + 3
VII) f(x)=
x+2
IV)f(x)=3x – 7
VIII) f(x)=– 4x +3x -
2
f(x)=ax +bx+c fonksiyonunun grafiği parabol olduğuna göre, f(x) ikinci dereceden fonksiyon olmalıdır. O halde,
2
Cevap: 5
1
2
6
Parabol
soru 1
soru 5
m – 4
2
+3x – 5 fonksiyonu ikinci dereceden fonksiyon olduf(x)=x
ğuna göre, m kaçtır?
f(x) = (m - 3)xm -7 + 4x - 2 fonksiyonunun grafiği parabol
olduğuna göre, m kaçtır?
A) 4
A) – 3
B) 5
D) 7
n – 3
f(x)=(m+4)x – 2x +5x – 1 fonksiyonu
fonksiyon olduğuna göre, m+n kaçtır?
ikinci
A) – 1
D) 5
B) 1
C) 2
f(x) = xm -14 + 6x - 2 fonksiyonunun grafiği parabol olduğuna göre, m'nin alabileceği değerler çarpımı kaçtır?
B) – 4
C) – 9
D) – 14
D) 3
E) 4
2
f(x)=(m – 3m – 4)x – 3x – 6 fonksiyonunun grafiği parabol olduğuna göre, m aşağıdaki değerlerden hangisini alamaz?
E) 9
2
C) 1
2
dereceden
A) – 1
B) – 1
soru 6
3
soru 3
E) 8
A) 1
KARTEZYEN EĞİTİM YAYINLARI
soru 2
C) 6
B) 2
soru 7
D) 4
E) 5
Aşağıdaki fonksiyonlardan hangisinin grafiği paraboldür?
A) f(x)=4x– 3
E) – 16
C) 3
C) f(x)=
2
B) f(x)=x – 3x – 10
x 2 + 2x
x +1
3
2
D)f(x)=x +2x – 3x
4
E) f(x)=x
soru 4
soru 8
3
n – 3
f(x)=(m – 5)x + x +4x+7 fonksiyonunun grafiği parabol olduğuna göre, m.n çarpımı kaçtır?
A) 25
B) 20
C) 15
D) 10
Aşağıdaki fonksiyonların kaç tanesinin grafiği paraboldür?
x2
2
-x
IV) f(x)=
I) f(x)=x
6
2
II) f(x)=– 2x +4
V) f(x)=– x+6
E) 5
2
III) f(x)=– x +2x – 8
A) 2
1 – C
2 – B
3 – E
4 – A
B) 3
5 – A
7
C) 4
6 – D
3
VI) f(x)=x – x
D) 5
7 – B
2
E) 6
8 – C
Parabol
2
f(x)=ax parabolünün grafiği
Konu Kavrama Çalışması
Aşağıda verilen fonksiyonların grafiğini çiziniz.
1 2
2
2
a) f(x)=x b) f(x)=2x c) f(x)= x
3
– 1
2
2
y=
2
0 =0
1 =1
2.1 =2
2
2.a =0
2
2.1 =2
1
1
(-1)2 =
3
3
1 2
.0 = 0
3
1 2 1
.1 =
3
3
2
1 2
x
3
2
1
(– 1) =1
y=x
y=2x
0
x'e farklı değerler vererek y değerlerini bulalım.
x
Bu üç grafiği aynı koordinat düzleminde çizelim.
2
Konu Kavrama Çalışması
Aşağıda verilen fonksiyonların grafiğini çiziniz.
2
2
a) f(x)=– x b) f(x)=– 2x c) f(x)=–
1 2
x
3
x'e farklı değerler vererek y değerlerini bulalım.
x
2
0
2
2
– (– 1) = – 1
y=– x
2
– 1
1
2
– 1 = – 1
2
2
– 0 =0
2
y=– 2x
– 2(– 1) =–2
– 2.0 =0
– 2.1 = – 2
Bu üç grafiği aynı koordinat düzleminde çizelim.
1 2
y= - x
3
1
1
- (-1)2 = 3
3
1
- .02 = 0
3
1
1
- .12 = 3
3
Uyarı
2
Bir parabolün kollarının yönünü x nin katsayısına bakarak anlayabiliriz.
2
a>0 ise f(x)=ax grafiğinin
2
a<0 ise f(x)=ax grafiğinin
kolları yukarı doğrudur.
kolları aşağı doğrudur.
2
Kavrama sorularında dikkat ederseniz, f(x)=ax parabollerinin grafiğinde |a| büyüdükçe parabolde kollar daralır, küçüldükçe
kollar açılır.
çözüm
kavrama sorusu
Kollar yukarı doğru olduğu için katsayılar pozitiftir. Parabolün
kolları y eksenine yaklaştıkça katsayıların değeri büyür.
Yandaki grafiğe göre a, b, c
sayılarını küçükten büyüğe
sıralayınız.
O halde 0<a<c<b dir.
Cevap: 0<a<c<b
8
Parabol
soru 1
soru 3
fonksiyonunun grafiği aşağıdakilerden hangisidir?
1
1
2
2
I. f(x)=– 3x , II. f(x)=– x , III. f(x)= - x 2 , IV. f(x)= - x 2
4
5
fonksiyonlarının grafiği aşağıdakilerden hangisi olabilir?
2
y=f(x)=– 3x
Yukarıdaki grafiğe göre, a, b, c, d sayılarının küçükten büyüğe sıralaması aşağıdakilerden hangisidir?
A) d<a<b<c
B) c<a<b<d
D) c<b<a<d
C) c<d<b<a
E) d<b<a<c
soru 4
KARTEZYEN EĞİTİM YAYINLARI
1
,
II. f(x)=3x
,
III. f(x)= x 2
I. f(x)=x
5
fonksiyonlarının grafiği aşağıdakilerden hangisi olabilir?
2
2
soru 2
1 – A
2 – E
3 – A
9
4 – D
Parabol
çözüm
kavrama sorusu
2
f(x)=x – 5x – 6 fonksiyonunun
a) x eksenini kestiği noktanın ordinatı sıfırdır.
a) x eksenini kestiği noktaları bulunuz.
y=0 için y=0=x – 5x – 6=(x – 6)(x+1)
b) y eksenini kestiği noktayı bulunuz.
x=6 veya x=– 1 dir. O halde x eksenini kestiği noktalar
(– 1, 0) veya (6, 0) dır.
Uyarı
2
b) y eksenini kestiği noktanın apsisi sıfırdır.
Bir parabolün x eksenini kestiği noktanın ordinatı (y değeri), y eksenini kestiği noktanın apsisi (x değeri) sıfırdır.
2
y=x – 5x – 6 ve x=0 için
y=0 – 5.0 – 6 =– 6 dır. O halde y eksenini kestiği nokta
(0, – 6) dır.
2
çözüm
kavrama sorusu
2
f(x)=x – 4x+4 fonksiyonunun eksenleri kestiği noktaları
bulunuz.
y=0 için x eksenini kestiği noktayı bulalım.
2
y=0 için y=0=x – 4x+4=(x – 2)(x – 2)
x=2 dir. O halde x eksenini kestiği nokta (2, 0) dır.
x=0 için y eksenini kestiği noktayı bulalım.
2
2
y=x – 4x+4 ve x=0 için y=0 – 4.0+4=4
O halde y eksenini kestiği nokta (0, 4) dür.
çözüm
kavrama sorusu
2
f(x)=x – x+2 fonksiyonunun eksenleri kestiği noktaları bulunuz.
y=0 için x eksenini kestiği noktayı bulalım.
2
y=0 için y=0=x – x+2
2
2
=b – 4ac=(– 1) – 4.1.2=– 7<0 reel kök yoktur.
O halde x eksenini kesmez.
x=0 için y eksenini kestiği noktayı bulalım.
2
2
y=x – x+2 ve x=0 için y=0 – 0+2=2
O halde y eksenini kestiği nokta (0, 2) dir.
çözüm
kavrama sorusu
(a, 0) ve (b, 0) noktaları x eksenini kestiği noktalardır.
2
y=0 için 0=– x – x+6=(– x – 3)(x – 2)
x=– 3=a veya x=2=b dir.
(0, c) noktası y eksenini kestiği noktadır.
2
y=– x – x+6 ve x=0 için
2
y=– 0 – 0+6=6=c dir.
O halde a+b – c=– 3+2 – 6=– 7 dir.
Cevap: – 7
2
Yandaki grafik f(x)=– x – x+6 parabolüne aittir.
a+b – c kaçtır, bulunuz.
10
Parabol
soru 1
soru 5
2
2
f(x)=x – 3x – 4 fonksiyonunun grafiği için aşağıdakilerden
hangisi veya hangileri doğrudur?
f(x)=– x +x – 12 parabolü için aşağıdakilerden hangisi veya hangileri doğrudur?
I) x eksenini (– 1, 0) ve (4, 0) noktalarında keser.
I) x eksenini kesmez.
II) y eksenini (0, – 4) noktasında keser.
II) y eksenini (0, – 12) noktasında keser.
III) f(x)=– x +x – 12 parabolünün kolları aşağı doğrudur.
2
III) f(x)= x – 3x – 4 parabolünün kolları yukarı doğrudur.
A) I, II ve III
soru 2
B) I ve II
C) I ve III
D) II ve III
E) Yalnız I
A) I ve II
B) I ve III
soru 6
B) 9
C) 8
D) 7
C) II ve III
D) I, II ve III
E) Yalnız II
Yandaki grafik,
2
f(x)=x – 7x – 8 fonksiyonunun grafiğinin x eksenini kestiği
noktalar arasındaki uzaklık kaçtır?
A) 10
2
2
f(x)=x – 9
parabolüne aittir.
E) 6
a – b+c kaçtır?
soru 3
KARTEZYEN EĞİTİM YAYINLARI
2
f(x)=x – 4x – 5 fonksiyonunun grafiğinin y eksenini kestiği
noktanın ordinatı kaçtır?
A) 5
B) 1
C) – 1
D) – 4
A) – 15
B) – 12
soru 7
C) – 9
D) – 8
E) – 3
Yandaki grafik,
2
f(x)=– x +mx – n
parabolüne aittir.
E) – 5
m.n çarpımı kaçtır?
A) – 9
soru 4
soru 8
2
f(x)=– x +6x – 9 fonksiyonun grafiğinin x eksenini kestiği
noktanın apsisi ile y eksenini kestiği noktanın ordinatı toplamı kaçtır?
A) – 12
B) – 6
B) – 9
C) – 6
D) 6
2 – B
3 – E
D) 3
E) 6
Yandaki grafik,
2
f(x)=ax +bx+c
parabolüne aittir.
a – b – c kaçtır?
E) 9
A) 6
1 – A
C) – 3
4 – C
B) 3
5 – D
11
C) 0
6 – A
D) – 3
7 – B
E) – 6
8 – E
Parabol
Parabolün Tepe Noktası
2
f(x)=ax +bx+c fonksiyonunun alabileceği en küçük veya en büyük değere bu fonksiyonun gösterdiği parabolün tepe noktası
denir. Tepe noktasının koordinatları T(r, k) diye gösterilir.
a>0 ise
a<0 ise
2
f(x)=ax +bx+c parabolünün tepe noktasının koordinatları T(r, k);
r=-
b
4ac - b2
ve k=f(r) formülleri ile bulunur. Tepe noktasının ordinatını k =
bağıntısıyla da bulabilirsiniz.
2a
4a
çözüm
kavrama sorusu
2
2
f(x)=3x – 12x – 1 parabolünün tepe noktasının koordinatlarını bulunuz.
f(x)=3x – 12x – 1 ise a=3 , b=– 12, c=– 1 dir.
r= -
-12
b
==2
2a
2.3
r=2 değerini fonksiyonda yerine yazalım.
2
k=f(r)=f(2)=3.2 – 12.2 – 1=12 – 24 – 1=– 13
O halde T(r, k)=T(2, – 13) dür.
Cevap: T(2, – 13)
çözüm
kavrama sorusu
2
f(x)=(m – 3)x – (5m – 1)x – 3 parabolünün tepe noktasının apsisi 2 olduğuna göre, m kaçtır, bulunuz.
Tepe noktasının apsisi r olduğu için r=2 dir.
a=m – 3, b=– (5m – 1)=– 5m+1 ve
r=-
-5m + 1 5m - 1
b
==
= 2 için
2a
2(m - 3) 2m - 6
5m – 1=2(2m – 6)=4m – 12
Cevap: – 11
5m – 4m=– 12+1 ise m=– 11 dir.
çözüm
kavrama sorusu
2
f(x)=x – mx – 2 parabolünün tepe noktasının ordinatı – 3 olduğuna göre, m'nin alabileceği değerleri bulunuz.
Tepe noktasının ordinatı k olduğu için k=– 3 dür.
a=1, b=– m, c=– 2 ve
4ac - b2
4.1.(-2) - (-m)2 -8 - m2
=
=
= -3 için
4a
4
4
k=
2
– 8 – m =– 12
2
m =4 ise m=2 veya m=– 2 dir.
Cevap: – 2 veya 2
(k=f(r) formülüyle de çözüm yapılabilir.)
çözüm
kavrama sorusu
2
2
f(x)=– x +mx – n parabolünün tepe noktası T(5, 5) olduğuna
göre, m+n toplamı kaçtır, bulunuz.
f(x)=– x +mx – n ise a=– 1, b=m, c=– n dir.
T(r, k)=T(5, 5) ise r=5, k=5 dir.
b
m
m
== = 5 ise m=10 dur.
r= 2a
2.(-1) 2
2
k=f(r)=f(5)=– 5 +m.5 – n=5
– 25+10.5 – n=5
n=20
O halde m+n=10+20=30
12
Cevap: 30
Parabol
soru 1
soru 5
2
2
f(x)=– 2x +8x – 6 parabolünün tepe noktasının koordinatları aşağıdakilerden hangisidir?
f(x)=3x +12x – m+3 parabolünün tepe noktasının ordinatı
(– 1) olduğuna göre, m kaçtır?
A) (2, – 2)
A) – 12
soru 2
B) (2, 2)
C) (2, 4)
D) (– 2, 2)
E) (– 2, – 2)
soru 6
2
B) – 11
C) – 10
D) – 9
E) – 8
2
f(x)=x +6x+5 parabolünün tepe noktasının koordinatları
toplamı kaçtır?
f(x)=x – 2x+m parabolünün tepe noktasının ordinatı 3 olduğuna göre, m kaçtır?
A) – 7
A) 1
C) – 1
D) 1
E) 7
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) – 4
2
soru 4
B) – 15
C) – 14
D) – 13
soru 7
C) 3
D) 4
E) 5
2
f(x)=(m – 3)x – 4x+5 parabolünün tepe noktasının apsisi
æç 1ö÷
ç- ÷ olduğuna göre, m kaçtır?
èç 8 ø÷
A) – 16
B) 2
f(x)=x – 2mx+m+2 parabolünün tepe noktasının ordinatı
(– 4) olduğuna göre, m'nin alabileceği pozitif değer kaçtır?
A) 1
E) – 12
B) 2
soru 8
2 C) 3
D) 4
E) 6
2
f(x)=(3m+1)x – (8m – 2)x – 6 parabolünün tepe noktasının apsisi 1 olduğuna göre, m kaçtır?
f(x)=x +(m – 2)x+n parabolünün tepe noktası T(– 3, 4) olduğuna göre, m+n toplamı kaçtır?
A) 4
A) 23
1 – B
B) 2
C) 1
2 – A
D) – 2
3 – D
E) – 4
4 – B
5 – E
13
B) 21
C) 20
6 – D
D) 19
7 – C
E) 18
8 – B
Parabol
çözüm
kavrama sorusu
2
f(x)=x +2mx+m+2 parabolünün tepe noktası x ekseni üzerinde olduğuna göre, m'nin alabileceği değerleri bulunuz.
Tepe noktası x ekseni üzerinde olduğuna göre, ordinatı k=0 dır.
a=1, b=2m, c=m+2 ve
b
2m
dan r = = -m
2a
2
2
k=f(– m)=(– m) +2m(– m)+m+2=0
r=-
Uyarı
2
m – 2m +m+2=0
2
– m +m+2=0
Tepe noktası y ekseninin üzerinde ise r=0 dır.
(– m – 1)(m – 2)=0
m=– 1
veya
m=2 dir.
Cevap: – 1 veya 2
çözüm
kavrama sorusu
Tepe noktası y ekseni üzerinde olduğuna göre apsisi r=0 dır.
9
parabolünün tepe noktası y ekseni
2
üzerinde olduğuna göre, m'nin alabileceği değerleri bulunuz.
2
2 Tepe noktasının koordinatları T(r, k) olan bir parabolün tepe noktası x ekseni üzerinde ise k=0 dır.
2
f(x)=– 2x +(m – 16)x+
2
a=– 2, b=m – 16 ve
r=-
b
m2 - 16 m2 - 16
==
2a
2.(-2)
4
m2 - 16
2
ve 0=m – 16 ise
4
m=– 4 veya m=4 dür.
r=0=
Cevap: – 4 veya 4
çözüm
kavrama sorusu
Tepe noktası y ekseni üzerinde olduğuna göre, apsisi r=0 dır.
Yandaki grafik
2
2
2
f(x)=mx – (m – 2m – 3)x+20
a=m, b=– m +2m+3 ve
parabolüne aittir.
r=-
Tepe noktası y ekseni üzerinde olduğuna göre, m kaçtır,
bulunuz.
r=0=
-m2 + 2m + 3 m2 - 2m - 3
b
dir.
==
2a
2m
2m
m2 - 2m - 3
2
ve 0=m – 2m – 3=(m – 3)(m+1) ise
2m
m=3 veya m=– 1 dir.
2
Parabolün kolları aşağı doğru olduğuna göre x nin katsayısı
m<0 olmalıdır.
O halde m=– 1 dir.
Cevap: – 1
14
Parabol
soru 1
soru 5
2 2
f(x)=– 3x – (m – 25)x+12 parabolünün tepe noktası y ekseni
üzerinde olduğuna göre, m'nin alabileceği değerler çarpımı
kaçtır?
Yandaki grafik
A) 25
Tepe noktası y ekseni üzerinde
B) 5
C) – 4
D) – 9
2
2
f(x)=mx +(m – 5m – 14)x+9
parabolüne aittir.
E) – 25
olduğuna göre, m kaçtır?
A) – 14
soru 2
2
B) – 7
soru 6
2
C) – 5
f(x)=x +(m – 3m – 10)x – 8 parabolünün tepe noktası y ekseni
üzerinde olduğuna göre, m'nin alabileceği değerler toplamı
kaçtır?
Yandaki grafik
A) – 10
Tepe noktası y ekseni üzerinde
B) – 3
C) 2
D) 3
D) – 2
2
E) 7
2
f(x)=mx – (m – 4m – 12)x – 4
parabolüne aittir.
E) 10
soru 3
KARTEZYEN EĞİTİM YAYINLARI
olduğuna göre, m kaçtır?
2 f(x)=x – 4mx+4 parabolünün tepe noktası x ekseni üzerinde
olduğuna göre, m'nin alabileceği değerler toplamı kaçtır?
A) 4
B) 2
C) 1
D) 0
A) 8
B) 6
soru 7
C) 4
D) 2
E) – 2
Yanda grafiği verilen
y=f(x) parabolünün denklemi
aşağıdakilerden hangisi olabilir?
E) – 1
2
2
A) f(x)=x +6
2
C) f(x)=– x – 4
B) f(x)=– x +4
2
D) f(x)=x – x – 1
2
E) f(x)=– x +3x
soru 4
soru 8
2 f(x)=x – 2mx+m+12 parabolünün tepe noktası x ekseni üzerinde olduğuna göre, m'nin alabileceği değerler çarpımı
kaçtır?
Aşağıda denklemi verilen parabollerden hangisinin tepe
noktası x ekseni üzerindedir?
2
A) 12
B) 6
C) – 1
D) – 6
2
A) y=– x +5
2
C) y= x +3x+2
E) – 12
B) y=– x – 6x
2
D) y=– x +3x – 2
2
E) y= x – 3x – 2
1 – E
2 – D
3 – D
4 – E
5 – D
15
6 – B
7 – A
8 – A
Parabol
Parabolle X Ekseninin Birbirine Göre Durumları
2
2
=b – 4ac
f(x)=ax +bx+c parabolünün diskriminantı
dir.
Bir parabolün x eksenine göre durumunu incelerken, bu parabolün diskriminantının değerine bakılmalıdır. Şimdi bu durumları
inceleyelim!
2
2
ax +bx+c=0 ikinci dereceden denkleminin kökleri y=f(x)=ax +bx+c parabolünün x eksenini kestiği noktaların apsisleridir.
1)
> 0 ise parabol x eksenini iki farklı noktada keser.
2)
=0 ise parabol x eksenine teğettir.
a)
=0
ve
r=-
pozitif tarafta teğettir.
veya
b
>0
2a
ise
parabol x eksenine
veya
3)
<0 ise parabol x eksenini kesmez.
b)
veya
=0
ve
r=-
negatif tarafta teğettir.
b
<0
2a
ise
parabol x eksenine
veya
çözüm
kavrama sorusu
2
f(x)=x – 4x+m – 2 parabolü x eksenini iki farklı noktada kestiğine göre, m'nin değer aralığını bulunuz.
>0 olmalıdır. a=1 , b=– 4 , c=m – 2 ve
2
2
=b – 4ac=(– 4) – 4.1.(m – 2)>0
16 – 4m+8>0
için
ise
6>m dir.
Cevap: m<6
çözüm
kavrama sorusu
2
f(x)=x – (m+3)x+8 parabolü x eksenine teğet olduğuna göre,
m'nin alabileceği değerleri bulunuz.
=0 olmalıdır. a=2 , b=– m – 3 , c=8 ve
2
2
2
=b – 4ac=(– m – 3) – 4.2.8=0 ise (– m – 3) =64 dür.
– m – 3=8
veya
m=– 11
– m – 3=– 8
veya
Cevap: – 11 veya 5
m=5
çözüm
kavrama sorusu
2
f(x)=x +(m+5)x+9 parabolü x eksenine pozitif tarafta teğet
olduğuna göre, m kaçtır, bulunuz.
2
=b – 4ac=0
ve
r= -
2
(m+5) – 4.1.9=0
m=1
>
olmalıdır.
-m - 5
>0
2
– 5>m
2
(m+5) =36
↓ ↓
m+5=6 m+5=– 6
2a
m=– 11
Cevap: – 11
O halde m<– 5 için m=– 11 dir.
çözüm
kavrama sorusu
2
f(x)=– 3x +6x – m+3 parabolü x eksenini kesmediğine göre,
m'nin değer aralığını bulunuz.
<0 olmalıdır. a=– 3 , b=6 , c=– m+3 ve
2
2
=b – 4ac=6 – 4.(– 3)(– m+3)<0
36 – 12m+36<0
ise
72<12 m
ise
ve
6<m dır.
Cevap: m>6
16
Parabol
soru 1
soru 5
2
f(x)=2x – 6x – m+3 parabolü x eksenini iki farklı noktada kestiğine göre, m'nin değer aralığı aşağıdakilerden hangisidir?
A) m > -
3
2
B) m < D) m > 3
soru 2
3
2
C) m >
1
parabolü x eksenine pozitif tarafta te4
ğet olduğuna göre, m kaçtır?
2
f(x)=x +(2m – 5)x+
3
2
A) 1
B) 2
soru 6
2
f(x)=– x – (2m – 4)x – 16 parabolü x eksenine negatif tarafta teğet olduğuna göre, m kaçtır?
C) 16
D) 15
B) – 4
C) – 2
D) 2
E) 6
E) 14
KARTEZYEN EĞİTİM YAYINLARI
soru 3
E) 5
A) – 6
B) 17
D) 4
2
f(x)=3x +12x+m – 5 parabolü x eksenini iki farklı noktada
kestiğine göre, m'nin alabileceği en büyük tam sayı değeri
kaçtır?
A) 18
C) 3
E) m > -3
2
soru 7
2
f(x)=– x +(m – 7)x – 25 parabolü x eksenine teğet olduğuna
göre, m'nin alabileceği değerlerin toplamı kaçtır?
f(x)=– 2x +4x – m – 6 parabolü x eksenini kesmediğine göre,
m'nin değer aralığı aşağıdakilerden hangisidir?
A) 17
A) m<4
soru 4
B) 14
C) 7
D) – 7
E) – 14
soru 8
1 2
x +6x+m – 3 parabolü x eksenine teğet olduğuna
2
göre, m kaçtır?
1 – A
B) – 10
2 – C
C) – 12
D) – 15
3 – B
C) m>– 3
D) m<– 4
E) m>– 4
2
f(x)=2x +5x – m+4 parabolü x eksenini kesmediğine göre,
m'nin alabileceği en büyük tam sayı değeri kaçtır?
f(x)= -
A) – 9
B) m>4
A) 2
E) – 18
4 – D
B) 1
5 – B
17
C) 0
6 – E
D) – 1
7 – E
E) – 2
8 – C
Parabol
Parabol Grafikleri
2
f(x)=ax +bx+c fonksiyonunun grafiğini çizerken şu ana kadar öğrendiğimiz parabol grafikleri ile ilgili bilgileri aşağıdaki sırada
uygularız.
1)
2)
a>0 ise parabolün kolları yukarı doğrudur, a<0 ise parabolün kolları aşağı doğrudur.
3)
Tepe noktasının koordinatları T(r, k) r = -
Parabolün eksenleri kestiği noktaları bulmak için x=0 alınırsa y değeri (ordinatı), y=0 alınırsa x değerleri (apsisleri) bulunur.
b
2a
, k=f(r) bulunur.
çözüm
kavrama sorusu
2
f(x)=x – 4x – 5 fonksiyonunun grafiğini çiziniz.
1. a=1>0 olduğu için kolları yukarı doğrudur.
2. Parabolün eksenleri kestiği noktalar,
Parabol grafiğini çizerken uygulanan adımlara dikkat
edeniz!
1. adım: a nın işaretine bakarak parabolün kollarının aşağımı yoksa yukarı yönlü mü olduğu
bulunur.
2
x=0 için y=0 – 4.0 – 5=– 5 ve (0, – 5) dir.
2
y=0 için x – 4x – 5=(x – 5)(x+1)=0
x=5 , x=– 1 ve (5, 0) , (– 1, 0) dır.
2. adım: Parabolün eksenleri kestiği noktalar bulu-
nur.
3. adım: Parabolün tepe noktasının koordinatları
bulunur.
-4
b
==2
2a
2.1
2
k=f(r)=f(2)=2 – 4.2 – 5=– 9
r=-
14243
3. Parabolün tepe noktasının koordinatları
T(2, – 9)
çözüm
kavrama sorusu
2
f(x)=– x +4x fonksiyonunun grafiğini çiziniz.
1. a=– 1<0 olduğu için kollar aşağı doğrudur.
2
2. x=0 için y=– 0 +4.0=0 ve (0, 0) dır.
2
y=0 için – x +4x=x(– x+4)=0
x=0 , x=4 ve (0, 0) ve (4, 0) dır.
b
4
==2 3. r = 2a
2.(-1)
T(2, 4)
2
k=f(r)=f(2)=– 2 +4.2=4
14243
çözüm
kavrama sorusu
2
f(x)=x – 2x+2 fonksiyonunun grafiğini çiziniz.
1. a=1>0 olduğu için kollar yukarı doğrudur.
2
2. x=0 için y=0 – 2.0+2=2 ve (0, 2) dir.
2
y=0 için x – 2x+2=0 ise
2
2
14243
=b – 4ac=(– 2) – 4.1.2=– 4<0 olduğu için x eksenini kesmez.
-2
b
3. r = == 1
2a
2
T(1, 1)
2
k=f(r)=f(1)=1 – 2.1+2=1
18
Parabol
soru 1
soru 3
2
2
f(x)=x +2x – 3
fonksiyonunun grafiği aşağıdakilerden hangisidir?
f(x)=x – 3x
fonksiyonunun grafiği aşağıdakilerden hangisidir?
KARTEZYEN EĞİTİM YAYINLARI
2
f(x)=– x +3x – 2
fonksiyonunun grafiği aşağıdakilerden hangisidir?
soru 4
2
f(x)=x – 4x+5
fonksiyonunun grafiği aşağıdakilerden hangisidir?
soru 2
1 – B
2 – A
3 – C
19
4 – D
Parabol
çözüm
kavrama sorusu
2
f(x)=4 – x
fonksiyonunun grafiğini çiziniz.
1. a=– 1<0 olduğu için kollar aşağı doğrudur.
2
2. x=0 için y=4 – 0 =4 ve (0, 4) dür.
2
y=0 için 4 – x =(2 – x)(2+x)=0
x=2 , x=– 2 ve (2, 0) , (– 2, 0) dır.
b
0
=
=0
3. r = 2a 2.(-1)
T(0, 4)
2
k=f(r)=f(0)=4 – 0 =4
14243
çözüm
kavrama sorusu
2
f(x)=x +3
fonksiyonunun grafiğini çiziniz.
1. a= 1>0 olduğu için kollar yukarı doğrudur.
2
2. x=0 için y=0 +3=3 ve (0, 3) dür.
2
2
y=0 için x +3=0 ve x = – 3
b
0
=
=0
2a 2.1
2 k=f(r)=f(0)=0 +3=3
3. r = 14243
denklemini sağlayan x değeri olmadığından x eksenini kesmez.
T(0, 3)
Uyarı
2
2
f(x)=ax +c nin grafiği f(x)=ax nin grafiğinin,
c>0 ise y ekseni boyunca c birim yukarı ötelenmesi ile c<0 ise y ekseni boyunca c birim aşağı ötelenmesi ile oluşur.
çözüm
kavrama sorusu
2
f(x)=x – 1
fonksiyonunun grafiğini çiziniz.
2
2
f(x)=x – 1 nin grafiği, f(x)=x nin grafiğinin 1 birim aşağı ötelenmesi ile çizilir.
çözüm
kavrama sorusu
2
f(x)=– 2x +4
fonksiyonunun grafiğini çiziniz.
2
2
f(x)=– 2x +4 nin grafiği, f(x)=– 2x nin grafiğinin 4 birim yukarı
ötelenmesi ile çizilir.
20
Parabol
soru 1
soru 3
2
2
f(x)=x – 9
fonksiyonunun grafiği aşağıdakilerden hangisidir?
f(x)=2x +6
fonksiyonunun grafiği aşağıdakilerden hangisi olabilir?
KARTEZYEN EĞİTİM YAYINLARI
f(x)=– x – 4
fonksiyonunun grafiği aşağıdakilerden hangisi olabilir?
soru 4
Aşağıdakilerden hangisinde fonksiyon yanlış verilmiştir?
1 – B
2
soru 2
2 – C
3 – A
21
4 – E
Parabol
çözüm
kavrama sorusu
2
f(x)=(x+2)
2
2
f(x)=(x+2) =x +4x+4
1. a=1>0 olduğu için kollar yukarı doğrudur.
fonksiyonunun grafiğini çiziniz.
2
2. x=0 için y=(0+2) =4 ve (0, 4) dür.
2
y=0 için (x+2) =0 , x=– 2 ve (– 2, 0) dur.
14243
b
4
= - = -2 2a
21
2
k=f(r)=f(– 2)=(– 2+2) =0
3. r = T(– 2, 0)
Uyarı
2
2
f(x)=a.(x – r) nin grafiği f(x)=ax nin grafiğinin,
r>0 ise x ekseni boyunca r birim sağa ötelenmesi ile r<0 ise x ekseni boyunca r birim sola ötelenmesi ile oluşur.
çözüm
kavrama sorusu
2
f(x)=(x – 3)
2
ve f(x)=(x+3)
fonksiyonlarının grafiğini çiziniz.
2
f(x)=– 2(x+2)
çözüm
kavrama sorusu
2
ve f(x)=– 2(x – 2)
fonksiyonlarının grafiğini çiziniz.
22
Parabol
soru 1
soru 3
f(x)=(x – 1)
fonksiyonunun grafiği aşağıdakilerden hangisidir?
KARTEZYEN EĞİTİM YAYINLARI
2
f(x)=(x+1)
fonksiyonunun grafiği aşağıdakilerden hangisidir?
A) 6
B) 5
soru 4
C) 4
D) 3
E) 2
Yukarıda bazı fonksiyonlar ve bu fonksiyonların grafikleri verilmiştir. Verilen grafiklerden kaç tanesi doğrudur?
A) 6
1 – B
Yukarıda bazı fonksiyonlar ve bu fonksiyonların grafikleri verilmiştir. Verilen grafiklerden kaç tanesi doğrudur?
soru 2
2
2 – A
B) 5
3 – A
23
C) 4
D) 3
E) 2
4 – B
Parabol
2
2
f(x)=a(x – r) ve f(x)=ax +c şeklindeki fonksiyonların grafiklerinin nasıl çizildiğini gördünüz. Şimdi de bu öğrendiklerinizi bir2
leştirerek f(x)=a(x – r) +c şeklindeki fonksiyonların grafiklerinin nasıl çizildiğini görelim. Bunun için aşağıda verdiğimiz kavrama
sorularını dikkatle inceleyiniz.
çözüm
kavrama sorusu
2
f(x)=(x – 2) +1 fonksiyonunun grafiğini çiziniz.
2
2
2
2
y=(x – 2) , y=x nin grafiği- y=(x – 2) +1, y=(x – 2) nin
nin 2 br sağa ötelenmesi ile grafiğinin 1 br yukarı ötelençizilir.
mesi ile çizilir.
Açıklama
2
Soruda verilen ifadeleri incelersek (x – 2) ifadesi tepe noktasını +x yönünde 2 br kaydırmak demektir.
+1 ifadesi tepe noktasını +y yönünde 1 br kaydırmak demektir.
çözüm
kavrama sorusu
2
f(x)=(x+3) –1 fonksiyonunun grafiğini çiziniz.
2
2
2
2
y=(x+3) , y=x nin grafiği- y=(x+3) – 1, y=(x+3) nin
nin 3 br sola ötelenmesi ile grafiğinin 1 br aşağı ötelençizilir.
mesi ile çizilir.
Açıklama
2
(x+3) ifadesi parabolün tepe noktasının – x yönünde 3 br kaydırmak demektir.
– 1 ifadesi parabolün tepe noktasını – y yönünde 1 br
kaydırmak demektir.
çözüm
kavrama sorusu
2
f(x)=– (x+2) +3 fonksiyonunun grafiğini çiziniz.
2
2
2
2
y=–(x+2) , y=– x nin grafi- y=–(x+2) +3, y=–(x+2) nin
ğinin 2 br sola ötelenmesi ile grafiğinin 3 br yukarı ötelençizilir.
mesi ile çizilir.
24
Parabol
soru 1
soru 3
2
f(x)=– (x – 2) +4
fonksiyonunun grafiği aşağıdakilerden hangisidir?
Yukarıda bazı fonksiyonlar ve bu fonksiyonların grafikleri verilmiştir. Verilen grafiklerden kaç tanesi doğrudur?
B) 7
C) 6
D) 5
E) 2
soru 4
2
f(x)=(x+1) +2
fonksiyonunun grafiği aşağıdakilerden hangisidir?
soru 2
KARTEZYEN EĞİTİM YAYINLARI
A) 8
Aşağıda verilenlerden hangisi yanlıştır?
2
A) f(x)=(x+3) +5 parabolünün tepe noktası T(– 3, 5) dir.
2
B) f(x)=(x – 3) +5 parabolünün tepe noktası T(3, 5) dir.
2
C) f(x)=2(x+3) – 5 parabolünün tepe noktası T(– 3, – 5) dir.
2
D) f(x)=– (x+2) +7 parabolünün tepe noktası T(2, 7) dir.
1
E) f(x)= - (x - 6)2 + 4 parabolünün tepe noktası T(6, 4) tür.
7
1 – A
2 – D
3 – C
25
4 – A
Parabol
Simetri Ekseni
2
f(x)=ax +bx+c fonksiyonunun grafiği tepe noktasının apsisinden geçen x=r doğrusuna göre simetriktir ve simetri ekseni
x=r= -
b
doğrusudur.
2a
r=
x1 + x 2
2
ve x1+x2= -
b
a
(Kökler toplamı) için
b
a = - b formülü elde edilir. Yani tepe noktasının apsisi
2
2a
r kökler toplamının yarısına eşittir.
r=
-
çözüm
kavrama sorusu
2
f(x)=2x +16x – 3 parabolünün simetri ekseni olan doğruyu
bulunuz.
x=r= -
b
doğrusu simetri ekseni ve a=2, b=16 olduğu için
2a
x=r= -
b
16
== -4
2a
2.2
x=– 4 doğrusu simetri eksenidir.
Cevap: – 4 doğrusu
çözüm
kavrama sorusu
Yandaki grafik y=f(x)
parabolüne aittir. Tepe
noktası T(3, k) olduğuna
göre, m kaçtır, bulunuz.
T(3, k) için r=3 dür. f(x) parabolünün simetri ekseni x=r=3 dür.
I. yol
m=3+5=8 dir.
x + x 2 -2 + m
II. yol 3 = 1
=
2
2
ise
6=– 2+m
8=m dir.
Cevap: 8
çözüm
kavrama sorusu
x=r doğrusu simetri ekseni olduğu için r=– 3 tür.
1 2
.x +(m – 4)x – 6 parabolünün simetri ekseni x=– 3
2
doğrusu olduğuna göre, m kaçtır, bulunuz.
f(x)= -
1
b
, b=m – 4 ve r= için
2
2a
m- 4
m- 4
r=== m - 4 = -3 ise m=1 dir.
æç 1÷ö
-1
2.ç- ÷÷
Cevap: 1
çè 2 ø
a= -
çözüm
kavrama sorusu
2 f(x)=(m – 5)x – 6x+8 parabolünün simetri ekseni 2x+3=0
doğrusu olduğuna göre, m kaçtır, bulunuz.
3
ve
2
3
x=r doğrusu simetri ekseni olduğu için r= - dir.
2
b
için
a=m – 5, b=– 6 ve r= 2a
-6
6
3
=
=r=ise
2(m - 5) 2m - 10
2
2x+3=0 için x= -
26
12=– 6m+30
– 18=– 6m
3=m dir.
Cevap: 3
Parabol
soru 1
soru 5
2 2 f(x)=3x – 12x+2 parabolünün simetri ekseni olan doğru
aşağıdakilerden hangisidir?
f(x)=(m– 4)x – (3m+2)x – 4 parabolünün simetri ekseni x=1
doğrusu olduğuna göre, m kaçtır?
A) x=6
A) – 10
B) x=4
soru 2
C) x=2
D) x=– 2
E) x=– 4
soru 6
f(x)=– x – 2x+4 parabolünün simetri ekseni olan doğru aşağıdakilerden hangisidir?
C) x= -
1
2
D) x=1
E) x=2
Yandaki grafik
f(x) parabolüne aittir.
Tepe noktası T(1, k)
D) – 4
E) – 3
A) 6
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) x=– 1
C) – 6
1 2 f(x)= x – (m – 2)x – 4 parabolünün simetri ekseni x=6 doğru3
su olduğuna göre, m kaçtır?
2 A) x=– 2
B) – 8
B) 4
soru 7
D) 2
E) 1
2 f(x)=(m+1)x +4x – 2 parabolünün simetri ekseni 3x – 2=0
doğrusu olduğuna göre, m kaçtır?
A) 4
olduğuna göre, m kaçtır?
C) 3
B) 2
C) – 1
D) – 2
E) – 4
A) – 1
soru 4
B) – 2
C) – 3
D) – 4
E) – 5
soru 8
2 Yandaki grafik
f(x) parabolüne aittir.
x2 – x1=10 olduğuna göre,
3x1+2x2 toplamı kaçtır?
A) – 21
1 – C
B) – 18
2 – B
C) – 16
A) 6
D) – 15
3 – C
f(x)=(2m+1)x – (3m – 4)x – 6 parabolünün simetri
2x – 1=0 doğrusu olduğuna göre, m kaçtır?
B) 5
C) 4
D) 3
ekseni
E) 2
E) – 12
4 – D
5 – A
27
6 – A
7 – E
8 – B
Parabol
çözüm
kavrama sorusu
|OA|=a için |OB|=3a dır.
| AB| 4a
=
=2a olur.
2
2
O halde C noktasının apsisi
2a – a=a ve f(x)'in tepe noktasının apsisi (r) dir.
-4
=2 için
r=a= 2
|AC|=
2
A(– a, 0) ve B(3a, 0) olduğundan, A(– 2, 0) ve B(6, 0) olur.
Yandaki grafik f(x)=x – 4x+m+2 parabolüne aittir.
Cevap: A(– 2, 0) ve B(6, 0)
|OB|=3|OA| olduğuna göre, A ve B noktalarının koordinatlarını bulunuz.
çözüm
kavrama sorusu
|OA|=a için |AB|=4a dır.
| AB| 4a
=2a olur.
=
2
2
O halde C noktasının apsisi
2a + a=3a ve f(x)'in tepe noktasının apsisi (r) dir.
6
=3 için a=1 dir.
r=3a= 2.(-1)
|AC|=
2
Yandaki grafik f(x)=– x +6x – m+1 parabolüne aittir.
A(a, 0) ve B(5a, 0) olduğundan A(1, 0) ve B(5, 0) olur.
|AB|=4.|OA| olduğuna göre, m kaçtır, bulunuz.
Bu noktalar parabol denklemini sağlar. A(1, 0) noktası için,
2
y=– x +6x – m+1
2
0=– 1 +6.1– m+1
0=– 1+6 – m+1
Cevap: 6
6=m dır.
çözüm
kavrama sorusu
2
| AB| 8
= =4 olur.
2
2
C noktasının apsisi f(x)'in
tepe noktasının apsisi (r) dir.
|AC|=
r= -
-4
=2 için
2.1
A(– 2, 0) ve B(6, 0) olur. Bu noktalar parabol denklemini sağlar. B(6, 0) ve
Yandaki grafik f(x)=x – 4x+m+3 parabolüne aittir.
|AB|=8 br olduğuna göre, m kaçtır, bulunuz.
2
y= x – 4x+m+3 için
2
0=6 – 4.6+m+3
0=36 – 24+m+3
– 15=m dir.
28
Cevap: – 15
Parabol
soru 1
soru 5
Yandaki grafik
Yandaki grafik
2
f(x)=x – 2x+m+2
2
parabolüne aittir.
f(x)=– x +10x – m+6
parabolüne aittir.
|OB|=3|OA|
4|OA|=3|AB|
olduğuna göre,
olduğuna göre, m kaçtır?
A noktasının apsisi kaçtır?
A) 18
A) – 4
B) – 3
soru 2
C) – 2
D) – 1
soru 6
Yandaki grafik
2
f(x)=– x – 8x+m – 1
olduğuna göre,
C) 3
D) 4
E) 6
KARTEZYEN EĞİTİM YAYINLARI
B) 2
C noktasının ordinatı kaçtır?
Yandaki grafik
2
A) 14
B) 13
soru 7
C) 12
parabolüne aittir.
f(x)=x – 2x – m+5
parabolüne aittir.
olduğuna göre, m kaçtır?
olduğuna göre, m kaçtır?
C) – 14
D) – 13
E) – 12
A) 18
B) 16
soru 8
C) 15
2
f(x)=x – 8x – m+5
D) 14
parabolüne aittir.
2
|AB|=10 br
olduğuna göre, m kaçtır?
olduğuna göre,
D) – 2
3 – C
C noktasının ordinatı kaçtır?
E) – 4
A) – 32
2 – B
parabolüne aittir.
|AB|=6|OA|
C) – 1
E) 13
f(x)=– 2x – 12x – m+1
Yandaki grafik
Yandaki grafik
1 – D
Yandaki grafik
|AB|=6 br
B) 2
E) 10
5|OA|=2|OB|
B) – 15
D) 11
2
f(x)=x – 3x+m+4
A) 4
|AB|=2|OA|
B noktasının apsisi kaçtır?
soru 4
parabolüne aittir.
olduğuna göre,
A) – 16
E) 30
f(x)=x – 8x+m – 2
|OA|=5|OB|
soru 3
D) 27
2
parabolüne aittir.
A) 1
C) 24
Yandaki grafik
B) 21
E) 0
4 – D
5 – D
29
B) – 31
C) 29
6 – C
D) 31
7 – E
E) 32
8 – E
Parabol
2
f(x)=ax +bx+c Fonksiyonunun En Küçük veya En Büyük Değerini Bulma
2
Tanım kümesi tüm reel sayılar verilmiş f(x)=ax +bx+c fonksiyonunun alabileceği en küçük değer veya en büyük değer tepe
noktasının ordinatıdır.
a>0 ise k=f(r) , f(x) fonksiyonunun alabileceği en küçük
değerdir.
a<0 ise k=f(r) , f(x) fonksiyonunun alabileceği en büyük
değerdir.
Fonksiyonun kolları sonsuza doğru gittiğinden a>0 ise fonksiyonun alabileceği en büyük değerini bulmayız.
Fonksiyonun kolları (–) sonsuza doğru gittiğinden a<0 ise
fonksiyonun en küçük değerini bulamayız.
çözüm
kavrama sorusu
2
f(x)=x – 8x+5
En küçük değer için k=f(r) bulunur.
-8
b
==4
2a
2.1
2
k=f(4)=4 – 8.4+5=– 11
fonksiyonunun alabileceği en küçük değeri bulunuz.
r=-
Tanım kümesi verilmediği takdirde tüm reel sayılar
kümesini tanım kümesi olarak düşüneceğiz.
f(x) fonksiyonunun alabileceği en küçük değer k=– 11 dir.
Cevap: – 11
çözüm
kavrama sorusu
2
f(x)=– 2x +12x – 3
En büyük değer için k=f(r) bulunur.
b
12
r===3
2a
2.(-2)
fonksiyonunun alabileceği en büyük değeri bulunuz.
2
k=f(3)=– 2.3 +12.3 – 3=15
f(x) fonksiyonunun alabileceği en büyük değer k=15 dir.
Cevap: 15
çözüm
kavrama sorusu
2
f(x)=x +8x+m – 5
En küçük değer 7 ise k=7 dir.
b
8
== -4
2a
2.1
2
k=f(– 4)=(– 4) +8(– 4)+m – 5=7
fonksiyonunun alabileceği en küçük değer 7 olduğuna göre,
m kaçtır, bulunuz.
r=-
16 – 32+m – 5=7
m=28 dir.
Cevap: 28
çözüm
kavrama sorusu
2
2
a) f(x)=2(x+3) – 8 fonksiyonunun alabileceği en küçük değeri bulunuz.
f(x)=a.(x – r) +k fonksiyonunun tepe noktası T(r, k) dır.
a) Tepe noktası: T(– 3, – 8) o halde en küçük değer k=– 8 dir.
2
b) f(x)=– 3(x – 4) +15 fonksiyonunun alabileceği en büyük
değeri bulunuz.
b) Tepe noktası: T(4, 15) o halde en büyük değer k=15 dir.
30
Parabol
soru 1
soru 5
2
f(x)=x +10x – 7
A) – 34
B) – 33
2
f(x)=2x +12x – m+3
fonksiyonunun alabileceği en küçük değer kaçtır?
C) – 32
D) – 31
fonksiyonunun alabileceği en küçük değer 5 olduğuna göre,
m kaçtır?
E) – 30
A) – 21
soru 2
soru 6
2
f(x)=2x – 6x – 1
soru 3
9
B) 2
11
C) 4
9
D) 4
f(x)=– x +8x – 3
soru 4
soru 7
B) 15
C) 14
D) 13
E) 12
2
A=a – 6a+1 ve B=– b – 4b+3
1 – C
2 – A
D) 1
3 – D
B) 10
C) 8
D) 7
E) 5
2
f(x)=– 5(x+4) – 6
fonksiyonunun alabileceği en büyük değer kaçtır?
A) – 2
C) – 1
E) – 4
2
soru 8
B) – 3
D) – 5
A) 15
olduğuna göre, A'nın alabileceği en küçük değer ile B nin
alabileceği en büyük değerin toplamı kaçtır?
A) – 8
C) – 6
fonksiyonunun alabileceği en küçük değer kaçtır?
2
B) – 7
1
olduğuna göre,
4
f(x)=3(x – 5) +7
fonksiyonunun alabileceği en büyük değer kaçtır?
A) 16
2
A) – 8
E) – 13
m kaçtır?
3
E) 2
2
D) – 15
fonksiyonunun alabileceği en büyük değer
KARTEZYEN EĞİTİM YAYINLARI
11
A) 2
C) – 18
f(x)=– x +5x+m+1
fonksiyonunun alabileceği en küçük değer kaçtır?
B) – 20
B) – 3
C) – 4
D) – 5
E) – 6
E) 7
4 – C
5 – B
31
6 – B
7 – D
8 – E
Parabol
çözüm
kavrama sorusu
Aşağıda verilen fonksiyonların görüntü kümesini bulunuz.
b
8
== -2
2a
2.2
2
k=f(– 2)=2(– 2) +8.(– 2)+5=– 3
2
a) r = -
2
a) f(x)=2x +8x+5
b) f(x)=– x +6x – 7
Fonksiyonun en küçük değeri k=– 3 olduğundan görüntü
kümesi: [– 3, ∞)
b
6
==3
b) r = 2a
2.(-1)
a>0 ise f(x) in
görüntü kümesi : [k, ∞)
k=f(3)=– 3 +6.3 – 7=2
Fonksiyonun en büyük değeri k=2 olduğundan görüntü
kümesi (–∞, 2] dir.
a<0 ise f(x) in
görüntü kümesi: (– ∞, k] dır.
2
Tanım kümesi sınırlı olan fonksiyonların görüntü kümesini bulurken fonksiyonun tepe noktasının yanında tanım kümesinin sınır
değerlerinin görüntüsüne de bakılır. Bulunan üç farklı değer fonksiyonun görüntü kümesinin sınırlarını verirler.
çözüm
kavrama sorusu
1.adım: En küçük değer için k=f(r) bulunur.
2
f:[– 3, 4) → R ve f(x)=x +2x – 7
b
2
2
== -1 ve k=f(– 1)=(– 1) +2.(– 1)– 7=– 8
2a
2.1
2.adım:Tanım kümesindeki [– 3, 4) için f(– 3) ve f(4) bulunur.
fonksiyonunun görüntü kümesini bulunuz.
r=-
Bu tarz sorularda izlemeniz gereken adımlar şunlardır;
1. adım: Tepe noktasının ordinatını f(r)=k yı bulun {Tepe noktasının apsisi r fonksiyonun tanım kümesinde değilse bu adımı atlamalısınız.}
2. adım: Tanım kümesinin sınır değerlerinin görüntüsü
bulunur.
3. adım: Bulunan değerlerin en küçüğü ve en büyüğü
görüntü kümesinin sınır değerleridir.
2
f(– 3)=(– 3) +2.(– 3)– 7=– 4
2
f(4)=4 +2.4 – 7=17
3.adım: – 8, – 4 ve 17 den en küçük değer – 8, en büyük değer 17 olduğundan görüntü kümesi [– 8, 17) dir. (4 tanım kümesinde olmadığı için 17 görüntü kümesinde yoktur.)
Cevap: [– 8, 17)
çözüm
kavrama sorusu
1.adım: ...
2
f:[4, 6) → R ve f(x)=x – 2x+3
r=1 fonksiyonun tanım kümesinde olmadığından f(r)=f(1) incelememize gerek yok.
fonksiyonunun görüntü kümesini bulunuz.
Parabolün tepe noktasının apsisi fonksiyonun tanım aralığında değil ise sınırları belirlerken r'yi incelemenize gerek
yoktur.
2.adım: Tanım kümesindeki [4, 6) için f(4) ve f(6) bulunur.
2
f(4)=4 – 2.4 + 3=11
2
f(6)=6 – 2.6 +3=27
3.adım: 11 ve 17 fonksiyonun en küçük ve en büyük değerleridir. Görüntü kümesi [11, 17] olur.
Cevap: [11, 17]
32
Parabol
soru 1
soru 5
2
2
f(x)=3x – 12x+2
Aşağıdakilerden hangisi f(x)=x – 4x+4 fonksiyonunun görüntü kümesinin elemanlarından değildir?
fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?
A) – 1
B) 0
C) 1
D) 2
E) 3
A) [– 12, ∞)
B) [– 11, ∞)
C) [– 10, ∞)
D) (– ∞, – 12] E) (– ∞, – 10)
soru 2
soru 6
2
2
f(x)=– 2x – 12x+5
f:[– 4, 1]→R ve f(x)=x +4x+8 olduğuna göre, aşağıdakilerden hangisi f(x) fonksiyonunun görüntü kümesinin elemanlarından değildir?
fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?
A) (– ∞, 24]
B) (– ∞, 23]
D) [23, ∞) A) 9
C) (– ∞, 22]
B) 10
C) 12
D) 13
E) 15
KARTEZYEN EĞİTİM YAYINLARI
E) [24, ∞)
soru 3
soru 7
2
2
f:[– 3, 5)→ R ve f(x)=x – 4x – 3
f:[– 1, 6]→R ve f(x)=x – 6x+10 fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?
fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?
A) (2, 18]
soru 4
B) [– 7, ∞)
D) [– 7, 18) A) [1, 17]
B) [1, 17)
C) [1, 10)
D) [10, 17)
E) (10, 17)
C) [– 7, 2)
E) [– 7, 18]
soru 8
2
2
fonksiyonunun görüntü kümesinde kaç tane tam sayı vardır?
f:[2, 5]→R ve f(x)=x +6x+10 fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?
A) 61
A) (10, 65]
1 – C
f:(– 5, 4]→ R ve f(x)=– x +6x+2
B) 62
2 – B
C) 63
D) 64
3 – E
E) 65
4 – D
5 – A
33
B) (10, 26]
C) (26, 65)
6 – E
D) [26, 65]
7 – A
E) (20, 65]
8 – D
Parabol
2
A(m, n) noktası f(x)=ax +bx+c fonksiyonunun grafiği üzerinde ise f(m)=n dir.
çözüm
kavrama sorusu
2
f(x)=3x – 5x+m – 2
Grafik A(2, – 3) noktasından geçtiğine göre, f(2)=– 3 dür.
2
fonksiyonunun grafiği A(2, – 3) noktasından geçtiğine göre,
m kaçtır, bulunuz.
f(x)=3x – 5x+m – 2
2
f(2)=3.2 – 5.2+m – 2=– 3
12 – 10+m – 2=– 3
m=– 3
Cevap: – 3
çözüm
kavrama sorusu
2
f(x)=– x +4x – 2
Grafik A(– 2, m) noktasından geçtiğine göre, f(– 2)=m dir.
2
fonksiyonunun grafiği A(– 2, m) noktasından geçtiğine göre,
m kaçtır, bulunuz.
f(x)=– x +4x – 2
2
f(– 2)=– (– 2) +4.(– 2)– 2=m
– 4 – 8 – 2=m
– 14=m
Cevap: – 14
çözüm
kavrama sorusu
2
f(x)=x +mx+n
Grafik A(1, 7) ve B(– 1, – 3) noktalarından geçtiğine göre,
f(1)=7 ve f(– 1)=– 3 dür.
fonksiyonunun grafiği A(1, 7) ve B(– 1, – 3) noktalarından geçtiğine göre, m.n çarpımı kaçtır, bulunuz.
2
f(x)=x +mx+n
f(1)=1+m+n=7 ise
m+n=6
2
m+n=6
– m+n=– 4
14243
f(– 1)=(– 1) +m.(– 1)+n=– 3 ise – m+n=– 4
denklem sistemini çözersek
n=1 ve m=5 bulunur.
O halde m.n=5.1=5
Cevap: 5
çözüm
kavrama sorusu
2
f(x)=x – 4x+4
Apsis ve ordinatı eşit olan noktaya A(m, m) diyelim. O halde
f(m)=m dir.
fonksiyonunun grafiği üzerinde apsisi ve ordinatı eşit olan
noktaları bulunuz.
2
f(m)=m – 4m+4=m
2
m – 5m+4=0
(m – 4)(m – 1)=0
m=4
veya m=1 dir.
O halde apsis ve ordinatı eşit olan noktalar (1, 1) veya (4, 4) dür.
34
Parabol
soru 1
soru 5
2
f(x)=x – 6x+m+4
2
f(x)=x – mx+n
fonksiyonun grafiği A(2, 10) noktasından geçtiğine göre,
m kaçtır?
fonksiyonunun grafiği A(2, 6) ve B(– 1, – 3) noktalarından
geçtiğine göre, m.n çarpımı kaçtır?
A) 12
A) – 4
soru 2
B) 13
C) 14
D) 15
E) 16
soru 6
2
f(x)=mx – 3x+m+1
B) – 2
C) 2
D) 4
E) 8
2
f(x)=2x +mx+n
fonksiyonun grafiği A(1, – 4) noktasından geçtiğine göre,
m kaçtır?
fonksiyonun grafiği A(1, 7) ve B(– 1, 5) noktasından geçti2
2
ğine göre, m – n kaçtır?
A) – 3
A) – 18
C) – 1
D) 1
E) 2
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) – 2
2
f(x)=– 2x +4x – 3
soru 7
B) – 15
C) – 12
D) 12
E) 15
2
f(x)=x – 4x+9
fonksiyonunun grafiği A(– 3, m) noktasından geçtiğine göre, m kaçtır?
fonksiyonun grafiği üzerinde ordinatı apsisinin 2 katı olan
noktanın koordinatları toplamı kaçtır?
A) – 33
A) 12
soru 4
B) – 24
C) – 9
D) 3
E) 9
soru 8
2
Aşağıdaki noktalardan kaç tanesi f(x)=x – 2x+3 fonksiyonunun grafiği üzerindedir?
I. (0, 3)
III. (– 1, 6)
V. (– 2, 3)
II. (1, 2)
IV. (2, 3)
VI. (4, 11)
A) 6
1 – C
B) 5
2 – C
C) 4
D) 3
3 – A
B) 9
C) 6
D) 4
E) 3
2
f(x)=x – 5x+5
fonksiyonunun grafiği üzerinde apsisi ve ordinatı eşit olan noktanın koordinatlar toplamı aşağıdakilerden hangisi
olabilir?
A) 4
E) 2
4 – B
B) 6
5 – D
35
C) 8
6 – B
D) 10
7 – B
E) 12
8 – D
Parabol
çözüm
kavrama sorusu
Grafik y eksenini (0, – 1) noktasında kesiyor. O halde nokta
parabol denklemini sağlar.
(0, – 1) ve y=a.(x+1)(x – 6) için
– 1=a.(0+1)(0 – 6)
–1=– 6a
1
=a dır.
6
Cevap:
Yukarıda f(x)=a(x+1)(x – 6) parabolünün grafiği verilmiştir.
1
6
a kaçtır, bulunuz.
çözüm
kavrama sorusu
Grafik y eksenini (0, 1) noktasında kesiyor. O halde nokta parabol denklemini sağlar.
(0, 1) ve y=a.(x+5)(x – 2) için
1=a.(0+5)(0 – 2)
1=– 10a
1
=a olur.
10
Yukarıda f(x)=a(x+5)(x – 2) parabolünün grafiği verilmiştir.
1
(x+5)(x – 2) ise
10
1
1
f(12)= (12+5)(12 – 2)= .17.10 =– 17 dir.
10
10
Cevap: – 17
f(12) kaçtır, bulunuz.
f(x)= -
çözüm
kavrama sorusu
Grafik y eksenini (0, – 3) noktasında kesiyor.
O halde parabol nokta denklemini sağlar.
2
(0, – 3) ve y=a(x – 2) – 4 için
2
Yukarıda f(x)=a(x – 2) – 4 parabolünün grafiği verilmiştir.
2
– 3=a(0 – 2) – 4
– 3=4a – 4
1=4a
1
=a dür.
4
a kaçtır, bulunuz.
Cevap:
1
4
çözüm
kavrama sorusu
Grafiğe bakıldığında (3, – 9) noktası f(x) parabolü üzerindedir.
O halde nokta parabol denklemini sağlar.
2
(3, – 9) ve y=a(x – 1) – 1 için
2
2
– 9=a(x – 1) – 1=a(3 – 1) – 1
– 9=4a – 1
– 8=4a
– 2=a dir.
2
f(x)=– 2(x – 1) – 1 ise
2
Yanda f(x)=a(x – 1) – 1 parabolünün grafiği verilmiştir.
2
f(a)=f(– 2)=– 2(– 2 – 1) – 1=– 18 – 1=– 19
f(a) kaçtır, bulunuz.
36
Cevap: – 19
Parabol
soru 1
soru 5
parabolünün grafiği verilmiştir.
B)
soru 2
1
4
C)
1
3
D)
Buna göre, a kaçtır?
1
2
E) 1
A)
1
8
B)
soru 6
parabolünün grafiği verilmiştir.
Buna göre, a kaçtır?
1
6
2
Yanda f(x)=a.(x – 1) – 4
Yanda f(x)=a.(x+3)(x – 2)
A)
1
6
C)
1
4
D)
1
2
E) 1
2
Yanda f(x)=a.(x+4)(x+1)
Yanda f(x)=a.(x+2) +3
parabolünün grafiği verilmiştir.
Buna göre, a kaçtır?
parabolünün grafiği verilmiştir.
1
8
soru 3
B)-
1
4
C) -
1
3
D) -
1
2
E) - 1
Yanda f(x)=a.x(x – 3)
1
3
soru 7
B)-
2
3
C) - 1
D) -
2
f(x) parabolünün
C) – 8
D) – 4
A)
E) – 2
8
3
soru 8
B)3
C)
10
3
C) 3
D) 4
3 – C
13
3
E) 5
A) – 68
2 – D
f(7)+f(– 9) toplamı kaçtır?
E)
parabolünün grafiği verilmiştir.
1 – C
11
3
2
parabolünün grafiği verilmiştir.
B) 2
Yanda f(x)=a.(x+1) – 1
A) 1
D)
Yanda f(x)=a.(x – 2)(x – 3)
Buna göre, f(a) kaçtır?
noktanın ordinatı kaçtır?
soru 4
y eksenini kestiği
B) – 12
E) - 3
parabolünün grafiği verilmiştir.
Buna göre, f(4) kaçtır?
A) – 16
3
2
Yanda f(x)=a.(x+2) +1
parabolünün grafiği verilmiştir.
A) KARTEZYEN EĞİTİM YAYINLARI
A) -
Buna göre, a kaçtır?
4 – B
5 – E
37
B) – 66
C) – 64
6 – A
D) – 62
7 – D
E) – 60
8 – B
Parabol
çözüm
kavrama sorusu
Grafiğe bakıldığında (0, 2) ve (– 2, 0) noktaları f(x) parabolü
üzerindedir. O halde bu noktalarparabol denklemini sağlar.
2
(0, 2) ve y=– 2x +mx+n için
2
2=– 2.0 +m.0+n
2=n
2
(– 2, 0) ve y=– 2x +mx+n için
2
2
Yukarıda f(x)=– 2x +mx+n fonksiyonunun grafiği verilmiştir.
0=– 2.(– 2) +m.(– 2)+2
m+n toplamı kaçtır, bulunuz.
0=– 8 – 2m+2
6=– 2m
– 3=m
Cevap: – 1
m+n=– 3+2=– 1 dir.
çözüm
kavrama sorusu
Grafiğe bakıldığında (1, 0) ve (2, 5) noktaları f(x) parabolü
üzerindedir. O halde bu noktalar parabol denklemini sağlar.
(1, 0)
2
ve
y=x +mx – n için
0=1+m – n
– 1=m – n
(2, 5)
2
Yukarıda f(x)=x +mx – n fonksiyonunun grafiği verilmiştir.
ve
2
5=2 +2m – n
1=2m – n
m – n=– 1
m.n çarpımı kaçtır, bulunuz.
2
y=x +mx – n için
2m – n=1
14243
denklem sistemini çözersek
m=2
,
n=3 olur.
m.n=2.3=6 dır.
Cevap: 6
çözüm
kavrama sorusu
Grafiğe bakıldığında (0, – 2) ve (2, 0) noktaları f(x) parabolü
üzerindedir. O halde bu noktalar parabol denklemini sağlar.
(0, – 2)
y=x +mx+n için
2
– 2=0 +m.0+n
– 2=n
(2, 0)
2
ve
2
ve
y=x +mx+n için
2
2
Yukarıda f(x)=x +mx+n fonksiyonunun grafiği verilmiştir.
0=2 +2m – 2
A noktasının apsisi kaçtır, bulunuz.
– 1=m
2
2
f(x)=x +mx+n=x – x – 2 ve A noktası x ekseni üzerinde olduğu için ordinatı y=0 dır.
2
O halde 0=x – x – 2
0=(x – 2)(x+1) ise x=2 veya x=– 1 dir.
A noktasının apsisi – 1 olur.
38
Cevap: – 1
Parabol
soru 1
soru 5
1 2
x +mx+n
4
fonksiyonunun grafiği
2
Yanda f(x)=– x +mx+n
fonksiyonunun grafiği verilmiştir.
C) 11
D) 12
E) 13
7
4
soru 6
2
Yanda f(x)=x +mx – n
fonksiyonunun grafiği
B) x = -
C) – 8
D) – 7
değeri kaçtır?
A) 1
soru 7
B)
4
5
C)
3
5
2
5
D)
E)
1
5
2
Yanda f(x)=– x +mx+n
fonksiyonunun grafiği verilmiştir.
verilmiştir. f(2) kaçtır?
verilmiştir.
E) – 6
Yanda f(x)=
7
2
a – c+b ifadesinin
1 2
x – mx+n
2
fonksiyonunun grafiği
E) x =
fonksiyonunun grafiği
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) – 9
7
4
C) x = 7
2
m.n çarpımı kaçtır?
7
2
Yanda f(x)=ax +bx+c
verilmiştir.
olan doğru aşağıdakilerden hangisidir?
D) x =
A) – 10
f(x) in simetri ekseni
A) x = -
soru 2
verilmiştir.
B) 10
Yanda f(x)= -
3m+4n toplamı kaçtır?
A) 9
f(x) fonksiyonunun alabileceği
en büyük değer kaçtır?
A) 2
B) 3
C) 4
D) 5
E) 6
A) 10
soru 4
soru 8
B) 9
C) 8
fonksiyonunun grafiği verilmiştir.
m+n toplamı kaçtır?
verilmiştir.
1 – C
2 – D
C) – 4
D) – 3
3 – B
1
3
B)
2
3
A noktasının apsisi kaçtır?
A)
B) – 5
Yanda f(x)=
A) – 6
E) 5
1 2
x +mx+n
3
fonksiyonunun grafiği
2
Yanda f(x)=2x +mx+n
D) 7
C) 1
D) 2
E) 3
E) – 2
4 – A
5 – E
39
6 – A
7 – B
8 – C
Parabol
çözüm
kavrama sorusu
f(x) parabolünün y eksenini kestiği nokta C'dir. x=0 için C nok2
tası bulunur. y=– 0 +2.0+3=3 dür.
f(x) parabolünün x eksenini kestiği noktalar A ve B dir. y=0 için
A ve B noktaları bulunur.
2
0=– x +2x+3=(– x+3)(x+1) ise
x=3 veya
x=– 1 dir.
|AB|=4 br
2
|OC|=3 br
Yukarıda f(x)=– x +2x+3 fonksiyonunun grafiği verilmiştir.
2
ABC üçgeninin alanı kaç br dir, bulunuz.
Alan(ABC)=
| AB|.|OC|
2
4.3
= 6 br 2
2
=
Cevap: 6
çözüm
kavrama sorusu
OABC kare olduğu için |OA|=|AB|=a olsun. O halde B noktasının koordinatları B(a, a) olur. B noktası parabol denklemini
sağlar.
2
B(a, a) ve y=x – 4x+4 için
2
a=a – 4a+4
2
0=a – 5a+4=(a – 4)(a – 1) ise
a=4 veya a=1 dir. f(x) parabolünün x eksenini kestiği nokta
2
2
x – 4x+4=(x– 2) =0 , x=2 ve
2
Yukarıda f(x)=x – 4x+4 fonksiyonunun grafiği verilmiştir.
|OA|<2 olduğu için a=1 dir.
2
OABC karesinin alanı kaç br dir, bulunuz.
2
2
O halde Alan(OABC)=1 =1 br dir.
Cevap: 1
çözüm
kavrama sorusu
|AB|=4|OA| olduğu için |OA|=a ve |AB|=4a dır. O halde B noktasının koordinatları B(a, 4a) olur. B noktası parabol
denklemini sağlar.
2
B(a, 4a) ve y=x – 6x+9 için
2
4a=a – 6a+9
2
0=a – 10a+9=(a – 1)(a – 9) ise
a=1 veya a=9 dur. f(x) parabolünün x eksenini kestiği nokta
2
2
x – 6x+9=(x – 3) =0 , x=3 ve |OA|<3 olduğu için a=1 dir.
2
Yukarıda f(x)=x – 6x+9 fonksiyonunun grafiği verilmiştir.
O halde Alan(OABC)=|OA|.|AB|
OABC dikdörtgen ve |AB|=4|OA| olduğuna göre,
=1.4
=4 br dir.
2
Alan(OABC) kaç br dir, bulunuz.
2
Cevap: 4
40
Parabol
soru 1
soru 5
2
Yanda f(x)=– x – 2x+8
Yanda f(x)=4x – 4x+1
fonksiyonunun grafiği
ABC üçgeninin
soru 2
C) 32
D) 24
1 2
Yanda f(x)= (x – 6x – 16)
4
fonksiyonunun grafiği
verilmiştir.
A)
1
256
soru 6
B)
1
64
C)
1
36
1
16
E)
1
9
2
Yanda f(x)=x – 12x+36
ABC üçgeninin
fonksiyonunun grafiği
OABC karesinin
2
2
alanı kaç br dir?
alanı kaç br dir?
C) 60
D) 80
E) 100
2
Yanda f(x)=– x +6x+7
fonksiyonunun grafiği
verilmiştir.
OAC üçgeninin
A) 25
KARTEZYEN EĞİTİM YAYINLARI
B) 40
D)
verilmiştir.
A) 20
2
verilmiştir.
soru 3
alanı kaç br dir?
E) 12
fonksiyonunun grafiği
OABC karesinin
2
B) 36
alanı kaç br dir?
A) 48
2
verilmiştir.
D) 4
E) 1
2
Yanda f(x)=x – 8x+16
fonksiyonunun grafiği
OABC dikdörtgen ve
2
alanı kaç br dir?
C) 9
verilmiştir.
soru 7
B) 16
|AB|=2|OA| olduğuna göre,
2
49
B)
2
A) 49
soru 4
C) 28
E) 7
A) 2
Alan(AÿOB)=12 br
2 – A
verilmiştir.
OABC dikdörtgen ve
n
kaçtır?
m
D) 4
E) 8
Yanda f(x)=x – 12x+36
|AB|=3.|OA| olduğuna göre,
Çevre(OABC) kaç br dir?
C) – 3
D) 3
E) 4
A) 30
1 – D
C) 2
fonksiyonunun grafiği
B) – 4
B) 1
2
verilmiştir.
olduğuna göre,
1
2
soru 8
1 2
Yanda f(x)= - x +mx+n
3
fonksiyonunun grafiği
A) – 6
Alan(OABC) kaç br dir?
49
D)
4
3 – B
4 – C
5 – D
41
B) 27
C) 24
6 – B
D) 16
7 – E
E) 12
8 – C
Parabol
çözüm
kavrama sorusu
OABC kare olduğu için |OA|=|AB|=a olsun. O halde B noktasının koordinatları B(– a, – a) olur. (B noktasının III. bölgede
olduğuna dikkat ediniz.) B noktası parabol denklemini sağlar.
2
B(– a, – a) ve y=x – 20 için
2
– a=(–a) – 20
2
0=a +a – 20=(a+5)(a – 4) ise a=– 5 veya a=4 dür.
Kenar uzunluğu pozitif olacağından a=4 olur.
2
Çevre(OABC)=4a=4.4=16 br
Yukarıda f(x)=x – 20 fonksiyonunun grafiği verilmiştir.
Cevap: 16
OABC karesinin çevresi kaç br dir, bulunuz.
çözüm
kavrama sorusu
Yukarıda f(x) parabolü verilmiştir.
f(x) parabolünün simetri ekseni x=r doğrusudur.
2
OABC kare olduğuna göre, Alan(OABC) kaç br dir, bulunuz.
-6 + 2
= -2 dir.
2
2
2
|OA|=2+2=4 için Alan(OABC)=4 =16 br dir.
O halde x=r=
Cevap: 16
çözüm
kavrama sorusu
2
2
Yukarıda f(x)=24 – x fonksiyonunun grafiği verilmiştir.
f(x)=24 – x parabolünün simetri ekseni y ekseni olduğundan
|OA|=|OB|=a ve ABCD kare olduğundan |AB|=|BC|=2a
olur. O halde C noktasının koordinatları C(a, 2a) olur. C noktası
parabol denklemini sağlar.
2
ABCD karesinin alanı kaç br dir, bulunuz.
C(a, 2a) ve y=24 – x
2
için
2
2a=24 – a
2
a +2a – 24=(a+6)(a – 4)=0 ise
a=– 6 veya a=4 dür.
Kenar uzunluğu pozitif olacağından a=4 olur.
2
2
2
2
Alan(OABC)=(2a) =4a =4.4 =64 br dir.
Cevap: 64
42
Parabol
soru 1
soru 5
2
Yanda f(x)=x – 30
fonksiyonunun grafiği
verilmiştir.
OABC karesinin
Yanda f(x) parabolü verilmiştir.
OABC kare olduğuna göre,
2
Alan(OABC) kaç br dir?
çevresi kaç br dir?
A) 8
soru 2
B) 12
C) 16
D) 20
A) 64
E) 24
soru 6
2
Yanda f(x)=x – 8
fonksiyonunun grafiği
verilmiştir.
OABC dikdörtgen ve
2
1
2
(– x +4x+12)
4
fonksiyonunun grafiği
verilmiştir.
C) 8
D) 18
E) 32
2
Yanda f(x)=x – 2
fonksiyonunun grafiği
verilmiştir.
A) 3
B) 6
soru 7
Yanda f(x)=15 – x
2
verilmiştir.
çevresi kaç br dir?
çevresi kaç br dir?
soru 4
E) 1
2
A) 40
Yanda f(x) parabolü verilmiştir.
OABC kare olduğuna göre,
Çevre(OABC) kaç br dir?
C) 24
D) 20
2
Yanda f(x)=x +m
verilmiştir.
ABCD karesinin
E) 12
fonksiyonunun grafiği
B) 32
soru 8
E) 15
fonksiyonunun grafiği
D) 1
D) 12
ABCD karesinin
C) 2
C) 9
OABC karesinin
B) 4
2
A) 8
Alan(OABC) kaç br dir?
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) 2
E) 16
olduğuna göre,
Alan(OABC) kaç br dir?
1
2
D) 25
OABC dikdörtgen
|AB|=2|OA| olduğuna göre,
A) C) 36
Yanda f(x)=
B) 49
2
alanı 64 br
A) 8
B) 12
C) 16
D) 20
olduğuna göre, m kaçtır?
E) 24
A) – 24
1 – D
2 – C
3 – B
4 – E
5 – A
43
B) – 15
C) – 12
6 – D
D) – 8
7 – C
E) – 4
8 – A
Parabol
Parabol Denklemi Yazma
 Herhangi üç noktası bilinen parabol denklemi
2
f(x)=ax +bx+c
biçiminde yazılır.
2
Verilen noktaların koordinatları f(x)=ax +bx+c denklemini sağlar.
çözüm
kavrama sorusu
2
A(0, – 5), B(1, – 8) ve C(– 1, 0)
A, B ve C noktaları y=ax +bx+c denklemini sağlar.
noktalarından geçen parabol denklemini yazınız.
A(0, – 5) için – 5=a.0+b.0+c ise – 5=c
2
B(1, – 8) için – 8=a.1 +b.1+c
– 8=a+b – 5 ise – 3=a+b
C(– 1, 0)
için
2
0=a.(– 1) +b.(– 1)+c
0=a – b – 5 ise 5=a – b
a+b=– 3
denklem sistemini çözersek
a – b=5
14243
a=1
,
b=– 4 bulunur.
2
2
O halde y=f(x)=ax +bx+c=x – 4x – 5 dir.
2
Cevap: f(x)=x – 4x – 5
çözüm
kavrama sorusu
A(2, 4),
yazınız.
2
B(1, 3) ve orijinden geçen parabol denklemini
A, B ve orijin noktaları y=ax +bx+c denklemini sağlar.
2
O(0, 0) için 0=a.0 +b.0+c ise 0=c
2
A(2, 4) için 4=a.2 +b.2+c
4=4a+2b+0 ise 2=2a+b
2
B(1, 3) için 3=a.1 +b.1+c
3=a+b+0 ise 3=a+b
2a+b=2
a+b=3
14243
denklem sistemini çözersek
a=– 1
,
2
b=4 bulunur.
2
O halde y=f(x)=ax +bx+c=– x +4x dir.
2
Cevap: f(x)=– x +4x
çözüm
kavrama sorusu
f(x) in grafiği (0, 4), (– 1, 0) ve (– 2, – 6) noktalarından geçiyor.
2
y=ax +bx+c eşitliğinde
(0, 4)
için
2
4=a.0 +b.0+c ise 4=c
2
(– 1, 0) için 0=a.(– 1) +b.(– 1)+c
0=a – b+4 ise – 4=a – b
2
(– 2, – 6) için – 6=a.(– 2) +b.(– 2)+c
Yukarıda grafiği verilen f(x) parabolünün denklemini yazınız.
a – b=– 4
2a – b=– 5
– 6=4a – 2b+4
– 10=4a – 2b ise – 5=2a – b
14243
denklem sistemini çözersek
a=– 1
2
ve
b=3 bulunur.
2
O halde y=f(x)=ax +bx+c=– x +3x+4 dir.
2
Cevap: f(x)=– x +3x+4
44
Parabol
soru 1
soru 5
A(0, – 3), B(3, 0) ve C(– 2, 5) noktalarından geçen parabol
denklemi aşağıdakilerden hangisidir?
2
A(1, 0), B(2, 0) ve C(– 1, 6) noktalarından geçen parabolün y eksenini kestiği noktanın ordinatı kaçtır?
2
A) f(x)=x – 2x – 3
B) f(x)=x – 4x – 3
2
A) – 2
B) – 1
C) 0
D) 1
E) 2
2
C) f(x)=– x +2x – 3
D) f(x)=x – 3x
2
E) f(x)=2x – x – 3
soru 2
soru 6
A(0, – 4), B(1, 0) ve C(4, 0) noktalarından geçen parabol
denklemi aşağıdakilerden hangisidir?
2
2
A) f(x)=– x – 5x – 4
B) f(x)=– x +5x – 4
2
2
C) f(x)=x – 5x+4
D) f(x)=– x +4x – 4
2
E) f(x)=– 2x +5x – 4
KARTEZYEN EĞİTİM YAYINLARI
soru 3
Yukarıda grafiği verilen f(x) parabolünün denklemi aşağıdakilerden hangisidir?
2
2
A) f(x)=– 2x +x
B) f(x)=– 2x +4x
2
2
C) f(x)=– x +2x
D) f(x)=– x +3x
2
E) f(x)=– x +x
A(1, – 4), B(3, 0) ve orijinden geçen parabol denklemi
aşağıdakilerden hangisidir?
2
2
A) f(x)=– 2x +5x
B) f(x)=x – 3x
2
2
C) f(x)=– x +3x
D) f(x)=2x +6x
2
E) f(x)=2x – 6x
soru 7
soru 4
A(1, 2), B(2, 6) ve orijinden geçen parabol denklemi aşağıdakilerden hangisidir?
2
Yukarıda f(x) parabolünün grafiği verilmiştir. f(5) in değeri
kaçtır?
2
A) f(x)=x +2x
B) f(x)=x +4x
2
2
C) f(x)=2x +2x
D) f(x)=x +x
A) 4
2
B) 5
C) 6
D) 7
E) 8
E) f(x)=x +3x
1 – A
2 – B
3 – E
4 – D
45
5 – E
6 – C
7 – C
Parabol
f(x)=a.(x – x1).(x – x2)
 Parabol x eksenini iki farklı noktada kesiyorsa bu parabolün denklemi
biçiminde yazılır.
çözüm
kavrama sorusu
Parabolün x eksenini kestiği noktaların apsisleri
x1=– 1 ve x2=3 için
y=f(x)=a.(x – x1).(x – x2) ise y=a.(x+1).(x – 3) tür.
Parabol (0, – 1) noktasından geçtiğinden
– 1=a.(0+1).(0 – 3) ise – 1=– 3a
1
= a bulunur.
3
O halde parabol denklemi
Yukarıda grafiği verilen ikinci dereceden f(x) fonksiyonunun denklemini yazınız.
f(x)=
1
1 2
1 2 2x
- 1 dir.
(x+1)(x – 3)= (x – 2x – 3)= x 3
3
3
3
1 2 2x
−1
Cevap: x −
3
3
çözüm
kavrama sorusu
Parabolün x eksenini kestiği noktaların apsisleri
x1=– 4 ve x2=2 için
y=f(x)=a.(x – x1).(x – x2) ise y=a.(x+4).(x – 2) dir.
Parabol (0, 2) noktasından geçtiğinden
2=a.(0+4).(0 – 2) ise 2=– 8a
1
a= bulunur.
4
O halde parabol denklemi
Yukarıda f(x) parabolü veriliyor. f(4) kaçtır, bulunuz.
f(x)= -
1
(x+4)(x – 2) için
4
f(4)= -
1
1
(4+4)(4 – 2)= - .8.2 = -4 tür.
4
4
Cevap: – 4
çözüm
kavrama sorusu
Parabolün x eksenini kestiği noktaların apsisleri
x1=– 1 ve x2=4 için
y=f(x)=a.(x – x1).(x – x2) ise y=a.(x+1).(x – 4) tür.
Parabol (1, 6) noktasından geçtiğinden
6=a.(1+1).(1 – 4) ise 6=– 6a
– 1=a bulunur.
2
O halde parabol denklemi f(x)=– 1(x+1)(x – 4)=– x +3x+4 tür.
Yukarıda grafiği verilen ikinci dereceden f(x) fonksiyonunun alabileceği en büyük değer kaçtır, bulunuz.
f(x) in alabileceği en büyük değer için k bulunur.
k=
4ac - b2
4.(-1).4 - 32 -16 - 9
25
=
=
=k =
tür.
4a
4.(-1)
-4
4
Cevap:
46
25
4
Parabol
soru 1
Yanda grafiği verilen
f(x) fonksiyonunun denklemi
verilmiştir.
Buna göre, f(7) kaçtır?
aşağıdakilerden hangisidir?
Yanda f(x) parabolü
ikinci dereceden
soru 5
2
A) – 9
2
A) f(x)=x – x – 5
B) f(x)=x +4x – 5
2
B) – 8
C) – 7
D) – 6
E) – 5
2
C) f(x)=x – 6x – 5
D) f(x)=x – 4x – 5
2
E) f(x)=x +6x – 5
soru 2
soru 6
Yanda grafiği verilen
ikinci dereceden
Yanda f(x) parabolü verilmiştir.
f(18)
oranı kaçtır?
Buna göre,
f(8)
f(x) fonksiyonunun denklemi
aşağıdakilerden hangisidir?
A) 6
-x 2 + 2x + 3
3
-x 2 - 2x + 3
-x 2 + 2x - 3
C) f(x) =
D) f(x) =
3
3
-x 2 + 4x - 3
E) f(x) =
3
A) f(x) = -x 2 + 2x + 3
Yanda grafiği verilen
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) f(x) =
B) 12
soru 7
ikinci dereceden
f(x) fonksiyonunun denklemi
f(x) fonksiyonunun
2
2
D) f(x)=x – 4x
A) -
2
E) f(x)=x +3x – 4
soru 4
soru 8
13
2
Yanda f(x) parabolü verilmiştir.
değer kaçtır?
2
C) f(x)=x +4x
alabileceği en küçük
B) f(x)=x – 3x – 4
2
E) 30
Yanda grafiği verilen
A) f(x)=2x – 8x
D) 24
ikinci dereceden
aşağıdakilerden hangisidir?
C) 18
B)- 6
C) -
11
2
D) - 5
E) -
9
2
Yanda grafiği verilen
Buna göre, f(2) kaçtır?
ikinci dereceden
f(x) fonksiyonunun
alabileceği en büyük
değer kaçtır?
A) 5
B) 6
C) 8
D) 10
E) 12
A) 7
1 – D
2 – B
3 – D
4 – E
B) 8
5 – C
47
C) 9
6 – B
D) 10
7 – E
E) 11
8 – C
Parabol
 Parabolün tepe noktası T(r, k) biliniyorsa bu parabolün denklemi
2
f(x)=a.(x – r) +k
biçiminde yazılır.
çözüm
kavrama sorusu
Tepe noktası T(r, k) bilinen parabol denklemi,
2
y=f(x)=a(x – r) +k ve T(2, – 1) için
2
y=a.(x – 2) – 1 dir.
Parabol (0, 3) noktasından geçtiğinden
Yukarıda grafiği verilen tepe noktası T(2, – 1) olan f(x) parabolünün denklemini yazınız.
2
3=a.(0 – 2) – 1
3=4a – 1
4=4a ise a=1 bulunur.
O halde parabol denklemi
2
2
2
f(x)=1.(x – 2) – 1=x – 4x+4 – 1=x –4x+3 dür.
2
Cevap: f(x)=x – 4x+3
çözüm
kavrama sorusu
Tepe noktası T(r, k) bilinen parabol denklemi,
2
y=f(x)=a(x – r) +k ve T(1, 0) için
y=a.(x – 1) +0 dır.
2
Parabol (0, 4) noktasından geçtiğinden
2
4=a.(0 – 1)
4=a bulunur.
O halde parabol denklemi
2
2
2
f(x)=4(x – 1) =4(x – 2x+1)=4x – 8x+4 tür.
Yukarıda grafiği verilen ikinci dereceden f(x) parabolünün
denklemini yazınız.
2
Cevap: f(x)=4x – 8x+4
çözüm
kavrama sorusu
Tepe noktası T(r, k) bilinen parabol denklemi,
y=f(x)=a(x – r) +k ve T(– 1, 2) için
y=a.(x+1) +2 dir.
2
Parabol (0, 4) noktasından geçtiğinden
2
2
4=a.(0+1) +2
4=a+2
2=a bulunur.
O halde parabol denklemi
Yukarıda f(x) parabolü veriliyor. f(2) kaçtır, bulunuz.
2
f(x)=2(x+1) +2 için
2
f(2)=2(2+1) +2=20 dir.
Cevap: 20
48
Parabol
soru 1
soru 5
Yanda grafiği verilen
aşağıdakilerden hangisidir?
2
B) f(x)=2x +8x+6
2
D) f(x)=x – 2x+3
A) – 3
2
A) f(x)=x – 4x+3
Buna göre, f(5) kaçtır?
f(x) parabolünün denklemi
Yanda f(x) parabolü verilmiştir.
tepe noktası T(– 2, –1) olan
B) – 6
C) – 9
D) – 12
E) – 18
2
C) f(x)=x +4x+3
2
E) f(x)=x +2x+3
soru 2
soru 6
Yanda grafiği verilen
Yanda f(x) parabolü verilmiştir.
tepe noktası y ekseni
Buna göre, f(6) kaçtır?
aşağıdakilerden hangisidir?
2
A) 6
B) 9
C) 12
D) 14
E) 26
2
A) f(x)=12 – 3x B) f(x)=12 – 4x
2
2
D) f(x)=12+3x
KARTEZYEN EĞİTİM YAYINLARI
C) f(x)=12 – 2x – x 2
E) f(x)=– 12 – 3x
soru 3
üzerinde olan
f(x) parabolünün denklemi
Yanda grafiği verilen
ikinci dereceden
f(x) fonksiyonunun denklemi
2
Buna göre, f(x)=– 9 eşitliğini
A) – 10
B) f(x)=x +4x+4
2
Yanda f(x) parabolü verilmiştir.
çarpımı kaçtır?
2
A) f(x)=x +2x+4
sağlayan x değerlerinin
aşağıdakilerden hangisidir?
soru 7
B) – 5
C) – 1
D) 1
E) 5
2
C) f(x)=2x +4x+4
D) f(x)=x – 4x+4
2
E) f(x)=x +4x+3
soru 4
soru 8
Yanda grafiği verilen
ikinci dereceden
1 – C
-x 2 - 6x - 9
3
-x 2 + 6x + 9
3
-x 2 + 6x - 9
2
C) f(x) = -x + 6x - 3
D) f(x) =
3
E) f(x) = -x 2 - 6x - 3
A) f(x) =
2 – A
Buna göre, (fof)(– 2) kaçtır?
aşağıdakilerden hangisidir?
B) f(x) =
3 – B
Yanda f(x) parabolü verilmiştir.
f(x) fonksiyonunun denklemi
A)
4 – D
19
4
5 – C
49
B)
17
4
C) 4
6 – D
D)
7 – E
13
4
E) 3
8 – B
Parabol
2
Bu bölümde grafiği verilen f(x)=ax +bx+c fonksiyonunun katsayıları a, b, c ve diskriminant ( ) işareti incelemesini yapacağız.
çözüm
kavrama sorusu
2
Grafik x eksenini 2 farklı noktada kestiği için
=b – 4ac>0
Parabolün kolları aşağı doğru olduğu için a<0
Parabol y eksenini pozitif tarafta kestiği için c>0
Parabolün tepe noktasının apsisi r = olduğu için b>0 dır.
a<0 , b>0 , c>0 ve
b
> 0 ve a<0
2a
>0 dır.
2
Yukarıda f(x)=ax +bx+c fonksiyonunun grafiği verilmiştir.
a, b, c ve
nin işaretlerini inceleyiniz.
çözüm
kavrama sorusu
2
Grafik x eksenini 2 farklı noktada kestiği için
=b – 4ac>0
Parabolün kolları yukarı doğru olduğu için a>0
Parabol y eksenini negatif tarafta kestiği için c<0
Parabolün tepe noktası y ekseni üzerinde olduğu için apsisi
b
= 0 ve b = 0 dır.
2a
>0 dır.
a>0 , b=0 , c<0 ve
r=-
2
Yukarıda f(x)=ax +bx+c fonksiyonunun grafiği verilmiştir.
a, b, c ve
nin işaretlerini inceleyiniz.
çözüm
kavrama sorusu
Grafik x eksenine teğet olduğuna göre
2
=b – 4ac=0
Parabolün kolları aşağı doğru olduğu için a<0
Parabol y eksenini negatif tarafta kestiği için c<0
Parabolün tepe noktasının apsisi r = olduğu için b<0 dır.
a<0 , b<0 , c<0 ve
b
< 0 ve a<0
2a
=0 dır.
2
Yukarıda f(x)=ax +bx+c fonksiyonunun grafiği verilmiştir.
a, b, c ve
nin işaretlerini inceleyiniz.
çözüm
kavrama sorusu
Grafik x eksenini kesmediği için
2
=b – 4ac<0
Parabolün kolları yukarı doğru olduğu için a>0
Parabol y eksenini pozitif tarafta kestiği için c>0
Parabolün tepe noktasının apsisi r = olduğu için b>0 dır.
a>0 , b>0 , c>0 ve
2
Yukarıda f(x)=ax +bx+c fonksiyonunun grafiği verilmiştir.
a, b, c ve
nin işaretlerini inceleyiniz.
50
<0 dır.
b
< 0 ve a>0
2a
Parabol
soru 1
soru 5
2
fonksiyonunun grafiği verilmiştir.
Yanda f(x)=ax +bx+c
fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdakilerden
Buna göre aşağıdakilerden
hangisi yanlıştır?
A) a>0
B) c<0
2
C) b – 4ac>0
D) b<0
E) a.b.c<0
soru 6
Yanda f(x)=ax +bx+c
Buna göre aşağıdakilerden
hangisi yanlıştır?
hangisi yanlıştır?
A) a<0
2
D) b >4ac
2
Yanda f(x)=ax +bx+c
fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdakilerden
soru 7
soru 4
B) b=0
2
fonksiyonunun grafiği verilmiştir.
E) a<0
soru 8
fonksiyonunun grafiği verilmiştir.
hangisi yanlıştır?
A) a.b.c<0
3 – D
Buna göre aşağıdakilerden
B) (a+b)(c – b)>0
C) a+b>0
2
D) b>c E) b – 4ac>0
2 – C
fonksiyonunun grafiği verilmiştir.
hangisi yanlıştır?
C) a.b.c<0 D) a+c>0 E) b<0<a
2
Buna göre aşağıdakilerden
1 – E
a+c
>0
b-a
Yanda f(x)=ax +bx+c
Yanda f(x)=ax +bx+c
A) c=0
2
Yanda f(x)=ax +bx+c
A) b < 4ac B) a.c
<0
D) b-c
E) f(a)>f(b)
hangisi yanlıştır?
C) c>0
2
D) b =4ac
2
A) b – 4ac>0
C) c=0
Buna göre aşağıdakilerden
hangisi yanlıştır?
2
B) b=0
E) b<0
KARTEZYEN EĞİTİM YAYINLARI
C) a.c+b.c>0
fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdakilerden
soru 3
2
E) b =4ac
2
verilmiştir.
B) c>0
D) a.b<0
Yanda f(x)=ax +bx+c
fonksiyonunun grafiği
A) a<0
a
c
2
C) b <
B) (a – b).c>0
hangisi yanlıştır?
A) b.c>0
soru 2
2
Yanda f(x)=ax +bx+c
4 – B
B) a +b
<0
a+c
D) a.(c+b)>0 5 – A
51
6 – E
E) C) a+b+c<0
4ac
>1
b2
7 – B
8 – B
Parabol
Parabol ile Doğrunun veya Parabol ile Parabolün Kesişim Noktalarını Bulma
Bir parabol ile doğrunun veya parabol ile parabolün kesişim noktalarını bulmak için iki denklem ortak çözülür. (İki fonksiyon
birbirine eşitlenir.)
çözüm
kavrama sorusu
2
f(x)=x – 5x+3 parabolü ile y=x – 2 doğrusunun kesişim
noktalarını bulunuz.
İki fonksiyon birbirine eşitlenir.
2
2
x – 5x+3=x – 2 ise x – 6x+5=0
2
x – 6x+5=(x – 1)(x – 5)=0 ise x=1 veya x=5 dir.
x=1 için y=x – 2=1 – 2=– 1 ⇒ (1, – 1)
x=5 için y=x – 2=5 – 2=3 ⇒ (5, 3)
O halde kesişim noktaları (1, – 1) ve (5, 3) dür.
çözüm
kavrama sorusu
2
2
f(x)=x – 6x+7 parabolü ile g(x)=x +1 parabolünün kesiştikleri noktayı bulunuz.
İki fonksiyon birbirine eşitlenir.
2
2
x – 6x+7=x +1 ise – 6x=– 6 ⇒ x=1
2
2
x=1 ise y=x +1=1 +1=2
O halde kesişim noktası (1, 2) dir.
çözüm
kavrama sorusu
2
m reel sayı olmak üzere f(x)=(m – 2)x +2x – m+6 parabollerinin geçtiği sabit noktaların koordinatlarını bulunuz.
m'ye vereceğimiz iki değerle elde edeceğimiz iki fonksiyonun
kesişim noktaları istenen noktalardır.
2
m=2 için y=(2 – 2)x +2x – 2+6 ⇒ y=2x+4
2
2
m=3 için y=(3 – 2)x +2x – 3+6 ⇒ y=x +2x+3
2
2
x +2x +3=2x +4 ise x =1
2
x =1 ise x=1 veya x=– 1 dir.
x=1 için y=2x+4=2.1+4=6 ⇒ (1, 6)
x=– 1 için y=2x+4=2.(– 1)+4=2 ⇒ (–1, 2)
O halde sabit noktaların koordinatları (1, 6) ve (– 1, 2) dir.
(m'ye vereceğimiz başka iki değer yine aynı noktaları verir.)
çözüm
kavrama sorusu
2
2
f(x)= x – (2m – 3)x – 8 ve g(x)=x +7x – n+4 fonksiyonlarının
grafikleri x eksenini aynı noktalarda kestiklerine göre, m+n
toplamı kaçtır, bulunuz.
x ekseni üzerindeki noktaların y=0 olduğundan f(x)=0 ve
g(x)=0 denklemlerinin çözüm kümeleri aynıdır.
2
O halde x – (2m – 3)x – 8=0
2
x +7x – n+4=0
denklemlerini birbirine eşitlersek
2
2
x – (2m – 3)x – 8=x +7x – n+4
Polinomların eşitliğinden,
– 2m+3=7
ve
m=– 2
– 8=– n+4
n=12
m+n=– 2+12=10
Cevap: 10
52
Parabol
soru 1
soru 5
2
2
f(x)=x – 3x+7 parabolü ile y=3x – 2 doğrusunun kesişim
noktası aşağıdakilerden hangisidir?
A) (3, 9)
B) (3, 7)
C) (3, 6)
D) (3, 2)
m reel sayı olmak üzere f(x)=(m – 3)x +3x – m+4 parabollerinin geçtiği sabit noktaların koordinatlarından biri aşağıdakilerden hangisidir?
E) (3,0)
A) (– 1, 2)
soru 2
soru 6
2
B) (1, – 4)
C) (– 1, 4)
D) (– 1, – 2)
E) (1,– 1)
2
f(x)=– x +5x – 2 parabolü ile y=x+1 doğrusunun kesişim
noktalarının ordinatlar toplamı kaçtır?
m reel sayı olmak üzere f(x)=(m+2)x +x – m – 5 parabollerinin geçtiği sabit noktaların ordinatları toplamı kaçtır?
A) 4
A) – 8
soru 3
C) 6
D) 7
E) 8
KARTEZYEN EĞİTİM YAYINLARI
B) 5
2
2
B) – 7
soru 7
C) – 6
D) – 5
E) – 4
2
2
f(x)=x – 4x+5 parabolü ile g(x)=x – 3 parabolünün kesiştikleri nokta aşağıdakilerden hangisidir?
f(x)=x +(2m+5)x – 6 ve g(x)=x – 3x+n+2 fonksiyonlarının grafikleri x eksenini aynı noktalarda kestiğine göre, m – n kaçtır?
A) (2, 1)
A) 8
soru 4
B) (2, 0)
C) (2, – 1)
D) (1, – 2)
E) (1,2)
soru 8
Yandaki grafiğe göre
y=– x +mx+n parabolü
A) – 3
1 – B
B) – 2
2 – C
C) -
A) 10
kesişmektedir. m.n çarpımı kaçtır?
3
2
D) – 2
3 – A
E) -
D) – 2
E) – 4
2
f(x)=x +(m+2)x – 5 ve g(x)=2x – 8x+3n+2 fonksiyonlarının
grafikleri x eksenini aynı noktalarda kestiğine göre, m+n toplamı kaçtır?
2
C) 2
2
x – 2y+2=0 doğrusu ile
A ve B noktalarında
B) 4
B) 4
C) – 6
D) – 8
E) – 10
1
2
4 – C
5 – D
53
6 – C
7 – B
8 – E
Parabol
Parabol ile Doğrunun veya Parabol ile Parabolün Birbirine Göre Durumları
Parabol ile doğrunun veya parabol ile parabolün kesişip kesişmediğini anlamak için ortak çözüm denklemi bulunur. (denklemleri
birbirine eşitlenir) Ortak çözüm denkleminin;
1)
2)
3)
>0 ise parabol ile doğru veya parabol ile parabol iki
farklı noktada kesişir.
=0 ise parabol ile doğru veya parabol ile parabol
birbirine teğettir.
<0 ise parabol ile doğru veya parabol ile parabol
kesişmez.
çözüm
kavrama sorusu
2
2
f(x)=x – 3x+m – 4 parabolü ile y=x+2 doğrusu iki farklı noktada kesiştiklerine göre, m nin değer aralığını bulunuz.
y=x – 3x+m – 4 ile y=x+2 nin ortak çözümünden elde edeceğimiz denklemde >0 olmalıdır.
2
2
x – 3x+m – 4=x+2 ise x – 4x+m – 6=0
2
2
=b – 4ac=(– 4) – 4.(m – 6)>0 ise 16 – 4m+24>0
Cevap: m<10
40>4m ve 10>m bulunur.
çözüm
kavrama sorusu
2
2
f(x)=x – 5x+m+2 parabolü ile y=3x+4 doğrusu birbirine teğet olduğuna göre, m kaçtır, bulunuz.
y=x – 5x+m+2 ile y=3x+4 ün ortak çözümünden elde edeceğimiz denklemde =0 olmalıdır.
2
2
x – 5x+m+2=3x+4 ise x – 8x+m – 2=0
2
2
=b – 4ac=(– 8) – 4.1.(m – 2)=0 ise 64 – 4m+8=0
Cevap: 18
72=4m ve 18=m bulunur.
çözüm
kavrama sorusu
2
2
2
f(x)=2x – mx – 3 parabolü ile g(x)=x – 4x – 12 parabolü birbirine teğet olduğuna göre, m nin alabileceği değerleri bulunuz.
2
y=2x – mx – 3 ile y=x – 4x – 12 ün ortak çözümünden elde
edeceğimiz denklemde =0 olmalıdır.
2
2
2
2x – mx – 3=x – 4x – 12 ise x +(4 – m)x+9=0
2
2
2
=b – 4ac=(4 – m) – 4.1.9=0 ise (4 – m) =36
4 – m=6 ise m=– 2
4 – m=– 6 ise m=10
Cevap: – 2 veya 10
çözüm
kavrama sorusu
2
2
f(x)=– 2x +3x – m+5 parabolü ile y=– x+3 doğrusu kesişmediğine göre, m nin değer aralığını bulunuz.
y=– 2x +3x – m+5 ile y=– x+3 ün ortak çözümünden elde
edeceğimiz denklemde <0 olmalıdır.
2
2
– 2x +3x – m+5=– x+3 ise – 2x +4x – m+2=0
2
2
=b – 4ac=4 – 4.(– 2).(– m+2)<0 ise 16 – 8m+16<0
32<8m ve 4<m bulunur.
54
Cevap: m>4
Parabol
soru 1
soru 5
2
2
f(x)=x +5x – m+3 parabolü ile y=– x+1 doğrusu iki farklı noktada kesiştiklerine göre, m'nin değer aralığı aşağıdakilerden
hangisidir?
2
f(x)=2x – x – m+2 parabolü ile g(x)=x +3x+m – 6 parabolünün birbirine teğet olduğuna göre, m kaçtır?
A) – 4
A) m> – 7
soru 2
B) m< – 7
C) m> – 8
D) m> – 9
B) – 2
soru 6
2
C) 1
D) 2
E) 4
E) m< – 9
2
2
2
f(x)=x +3x+m – 1 parabolü ile g(x)=– x – x – m+5 parabolü iki
farklı noktada kesiştiklerine göre, m'nin değer aralığı aşağıdakilerden hangisidir?
f(x)=2x +mx+5 parabolü ile g(x)=x +3x+1 parabolü birbirine teğet olduğuna göre, m'nin alabileceği değerler çarpımı
kaçtır?
A) m>4
A) – 8
C) m<5
D) m<3
E) m>3
KARTEZYEN EĞİTİM YAYINLARI
soru 3
B) m<4
2
11
2
B)
soru 4
11
4
C)
17
4
D)
19
4
E)
21
4
soru 8
B) – 80
C) – 60
D) – 40
2 – B
3 – E
B) m>0
C) m<0
D) m>3
E) m>6
2
2
f(x)=3x – 4x – m+5 parabolü ile g(x)=2x – 4x+m – 1 parabolü
kesişmediğine göre, m'nin alabileceği en büyük tam sayı
değeri kaçtır?
E) – 20
A) 5
1 – A
E) – 4
A) m<6
2
D) – 5
f(x)=3x – 5x+m – 2 parabolü ile y=x+1 doğrusu kesişmediklerine göre, m'nin değer aralığı aşağıdakilerden hangisidir?
f(x)=x +mx+3 parabolü ile y=2x – 13 doğrusu birbirine teğet
olduğuna göre, m'nin alabileceği değerler çarpımı kaçtır?
A) – 100
soru 7
C) – 6
2
f(x)=x +4x+m – 4 parabolü ile y=3x+1 doğrusu birbirine teğet olduğuna göre, m kaçtır?
A)
B) – 7
4 – C
B) 4
5 – D
55
C) 3
6 – B
D) 2
7 – E
E) 1
8 – D
Parabol
çözüm
kavrama sorusu
2
f(x)=x +7x+m parabolü ile y=x+4 doğrusu A ve B noktalarında kesişmektedir. [AB] doğru parçasının orta noktasının
koordinatlarını bulunuz.
İki fonksiyonun birbirine eşitlenir.
2
2
x +7x+m=x+4 ise x +6x+m – 4=0
2
x +6x+m – 4=0 denkleminin kökleri x ve x2 olmak üzere
A(x1, y1), B(x1, y1) ve C; [AB] nin orta noktası olmak
æ x + x 2 y1 + y 2 ö÷
,
üzere C nin koordinatları C çç 1
÷ olduğuèç 2
2 ø÷
nu hatırlayınız.
x1+x2= -
b
6
= - = -6 bulunur.
a
1
C noktasının apsisi
x1 + x 2
6
= - = -3
2
2
C noktası y=x+4 doğrusu üzerinde olduğundan
x=– 3 için y=– 3+4=1
O halde C noktasının koordinatları (– 3, 1) dir.
Cevap: (– 3, 1)
çözüm
kavrama sorusu
2
f(x)=x – 3x+1 parabolünün y=x – 5 doğrusuna en yakın
noktasının koordinatlarını bulunuz.
Parabolün üzerinde aldığımız y=x – 5 doğrusuna en
yakın nokta A'dan teğet geçen y=x – 5 doğrusuna paralel y=x+m doğrusudur.
2
O halde y=x – 3x+1 ile
Paralel doğruların eğimlerinin birbirine eşit olduğunu
hatırlayınız.
y=x+m birbirlerine teğettir.
2
2
x – 3x+1=x+m ise x – 4x+1 – m=0
2
2
=b – 4ac=(– 4) – 4.(1 – m)=0
16 – 4+4m=0
m=– 3 bulunur.
2
2
m=– 3 ve x – 4x+1 – m=0 ise x – 4x+4=0
↓
– 3
2
2
x – 4x+4=(x – 2) =0 ise x=2
2
2
x=2 ise y=x – 3x+1=2 – 3.2+1=– 1 dir.
O halde A(2, – 1) elde edilir.
Cevap: (2, – 1)
çözüm
kavrama sorusu
d doğrusunun denklemini yazalım. Orijinden geçen doğruların
denklemi y=mx şeklindedir. A(a, 2a) denklemi sağlar. O halde
2a=m.a için m=2 bulunur. d doğrusunun denklemi y=mx=2x
2
y=x +k ile y=2x in ortak çözümünden elde edeceğimiz
2
2
denklemde =0 olmalıdır. x +k=2x ise x – 2x+k=0
2
2
=b – 4ac=(– 2) – 4.1.k=0
2
Yukarıdaki grafiğe göre, f(x)=x +k parabolü ile orijinden ve
A(a, 2a) noktasından geçen d doğrusu birbirine A noktasında
teğettir, k kaçtır, bulunuz.
56
4 – 4k=0
1=k dir.
Cevap: 1
Parabol
soru 1
soru 5
2
2
f(x)=x – 5x+m parabolü ile y=– x+9 doğrusu A ve B noktalarında kesişmektedir. [AB] nin orta noktasının koordinatları
aşağıdakilerden hangisidir?
f(x)=x – 5x+11 parabolünün y=x – 4 doğrusuna en yakın
noktasının koordinatları aşağıdakilerden hangisidir?
A) (3, – 1)
A) (– 2, 11)
soru 2
B) (2, 11)
C) (2, 7)
D) (– 2, – 7)
B) (3, 5)
soru 6
2
f(x)=x +6x+1 parabolünün y=– 2x – 16 doğrusuna en yakın noktasının koordinatları aşağıdakilerden hangisidir?
D) (– 3, 3)
2
y=mx+n doğrusunun f(x)=x +5x – 4 parabolünü (2, – 3) noktasına göre, simetrik iki noktada kestiğine göre, n kaçtır?
A) – 18
B) – 19
C) – 20
D) – 21
B) (– 4, 7)
C) (– 4, 8)
D) (– 4, – 9)
E) (– 4, – 7)
E) (– 3, – 13)
E) – 22
KARTEZYEN EĞİTİM YAYINLARI
soru 3
C) (– 3, 11)
E) (3, 6)
A) (– 4, – 8)
B) (3, – 5)
D) (– 2, 25)
2
f(x)=x +3x+m – 2 parabolü ile y=– 3x+4 doğrusu A ve B noktalarında kesişmektedir. [AB] nin orta noktasının koordinatları aşağıdakilerden hangisidir?
A) (– 3, 13)
C) (2, 5)
E) (2, – 2)
soru 7
Yandaki grafiğe göre
2
f(x)=x – 2x+k parabolü ile
orijinden ve A(a, 4a)
noktasından geçen
d doğrusu birbirine
A noktasında teğettir. k kaçtır?
A) 1
soru 4
soru 8
f(x)=x +3x – 2 parabolünün y=x – 6 doğrusuna en yakın
noktasının apsisi kaçtır?
B) – 2
C) – 1
D) 1
C) 9
D) 16
E) 25
Yandaki grafiğe göre
2
A) – 3
B) 4
2
f(x)=x +k parabolü ile orijinden
ve A(a, 6a) noktasından
E) 2
geçen d doğrusu birbirine
A noktasında teğettir.
A noktasının apsisi kaçtır?
A) 2
1 – C
2 – A
3 – D
4 – C
B) 3
5 – B
57
C) 4
6 – E
D) 6
7 – C
E) 9
8 – B
Parabol
Eşitsizlik Grafikleri
Eşitsizlik grafiği çizilirken, grafik eşitlik var gibi çizilir ve grafiğin uygun kısmı grafik üzerinde olmayan bir nokta test edilerek taranır.
çözüm
kavrama sorusu
y=3x – 3 doğrusunun grafiğini çizelim.
y≥3x – 3 eşitsizliğinin grafiğini çiziniz.
x=0 için y=3.0 – 3=– 3 , (0, – 3)
y=0 için 0=3x – 3 , (1, 0)
(0, 0) noktasını y≥3x – 3
eşitsizliğinde test ettiğimizde 0≥– 3 ifadesinin
doğru olması, (0, 0) noktasının olduğu tarafı taramamızı sağladı.
çözüm
kavrama sorusu
y= – 2x doğrusunun grafiğini çizelim.
y< – 2x eşitsizliğinin grafiğini çiziniz.
x=0 için y=– 2.0=0 , (0, 0)
x=1 için y=– 2.1=– 2 , (1, – 2)
(1, 0) noktasını test edelim. (1, 0) ve y≤– 2x için
0≤– 2 yanlış olduğu için
(1, 0) noktasının olduğu
tarafı taramadık.
Grafiğin kesik kesik çizilmesi eşitliğin olmamasındandır.
çözüm
kavrama sorusu
2
y≥x eşitsizliğinin grafiğini çiziniz.
2
y=x parabolünün grafiğini
çizelim.
(0, 1) noktasını test edelim.
2
(0, 1) ve y≥x için 1≥0 doğru olduğu için (0, 1) noktasının olduğu tarafı taradık.
çözüm
kavrama sorusu
2
2
y=– x parabolünün grafiğini çizelim.
y> – x eşitsizliğinin grafiğini çiziniz.
58
(0, – 1) noktasını test ede2
lim. (0, – 1) ve y>– x için
– 1>0 yanlış olduğu için
(0, – 1) noktasının olduğu
tarafı taramadık.
Parabol
soru 1
soru 3
2
y<2x – 4
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
y<2x
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
KARTEZYEN EĞİTİM YAYINLARI
soru 4
2
y≥– 3x
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
y≥3x
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
soru 2
1 – B
2 – C
3 – A
59
4 – E
Parabol
çözüm
kavrama sorusu
2
2
y=– x +4 parabolünün grafiğini çizelim.
y< – x +4 eşitsizliğinin grafiğini çiziniz.
(0, 0) noktasını test edelim.
2
(0, 0) ve y<– x +4 için 0<4
doğru olduğu için (0, 0) noktasının olduğu tarafı taradık.
çözüm
kavrama sorusu
2
2
y=x – 2x – 8 parabolünün grafiğini çizelim.
y≤ x – 2x – 8 eşitsizliğinin grafiğini çiziniz.
(0, 0) noktasını test edelim.
2
(0, 0) ve y≤x – 2x – 8 için
0≤ – 8 yanlış olduğu için
(0, 0) noktasının olduğu tarafı taramadık.
çözüm
kavrama sorusu
2
2
y=– x +3x parabolünün grafiğini çizelim.
y>– x +3x eşitsizliğinin grafiğini çiziniz.
(0, 1) noktasını test edelim.
2
(0, 1) ve y>– x +3x için 1>0
doğru olduğu için (0, 1) noktasının olduğu tarafı taradık.
çözüm
kavrama sorusu
2
2
y=x – 2x+4 parabolünün grafiğini çizelim.
y≥ x – 2x+4 eşitsizliğinin grafiğini çiziniz.
(1, 0) noktasını test edelim.
2
60
(1, 0) ve y≥x – 2x+4 için
0≥3 yanlış olduğu için (1, 0)
noktasının olduğu tarafı taramadık.
Parabol
soru 1
soru 3
2
2
y≥– x +2
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
y≤x – 2x
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
soru 2
KARTEZYEN EĞİTİM YAYINLARI
2
y<– x +3x+4
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
soru 4
2
y>x – 4x+5
eşitsizliğinin grafiği aşağıdakilerden hangisidir?
1 – E
2 – D
3 – C
61
4 – A
Parabol
çözüm
kavrama sorusu
2
y>x ve y≤x+2 eşitsizliklerinin sağlandığı ortak bölgeyi
koordinat düzleminde gösteriniz.
İki grafiği aynı koordinat düzleminde çizelim ve ortak bölgeyi
tarayalım.
çözüm
kavrama sorusu
2
2
y>x +1 ve y≤3 – x eşitsizliklerinin sağlandığı ortak bölgeyi koordinat düzleminde gösteriniz.
İki grafiği aynı koordinat düzleminde çizelim ve ortak bölgeyi
tarayalım.
çözüm
kavrama sorusu
2
y≤x – 8 eşitsizliğini sağlayan noktalar N, H, G, C, B, A
2
Yandaki grafiğe göre, y≤x – 8 ve y≥– 2x eşitsizliklerinin
sağlandığı noktaları bulunuz.
y≥– 2x eşitsizliğini sağlayan noktalar A, I, M, N, H
O halde ortak noktalar A, H ve N dir.
62
Parabol
soru 1
soru 3
2
2
2
y≥x ve y<x+6 eşitsizliklerinin sağlandığı bölge aşağıdakilerden hangisidir?
y≤x +1 ve y>x – 3 eşitsizliklerinin sağlandığı ortak bölge
aşağıdakilerden hangisidir?
soru 2
2
2
y<x – 2x – 3 ve y≤4 – x eşitsizliklerinin sağlandığı bölge
aşağıdakilerden hangisidir?
KARTEZYEN EĞİTİM YAYINLARI
soru 4
Yandaki grafiğe göre
2
y≤x – 2, y≤x eşitsizliklerinin
A) {C, D, E, F}
aşağıdakilerden hangisidir?
B) {D, E}
D) {C, D, E} C) {C, D}
E) {A, B, C, D, E, F}
soru 5
sağlayan eşitsizlik sistemi
aşağıdakilerden hangisidir?
2
2
A) y>x +x – 2 B) y>x – x – 2
y≤– x+2 y<– x+2
2
2
C) y>x – x – 2 D) y≥x – x – 2
y≤x+2 y≤– x+2
2
E) y>x – x – 2
y≤– x+2
2 – C
Yandaki grafikte taralı bölgeyi
1 – B
sağladığı noktalar
3 – A
63
4 – D
5 – E