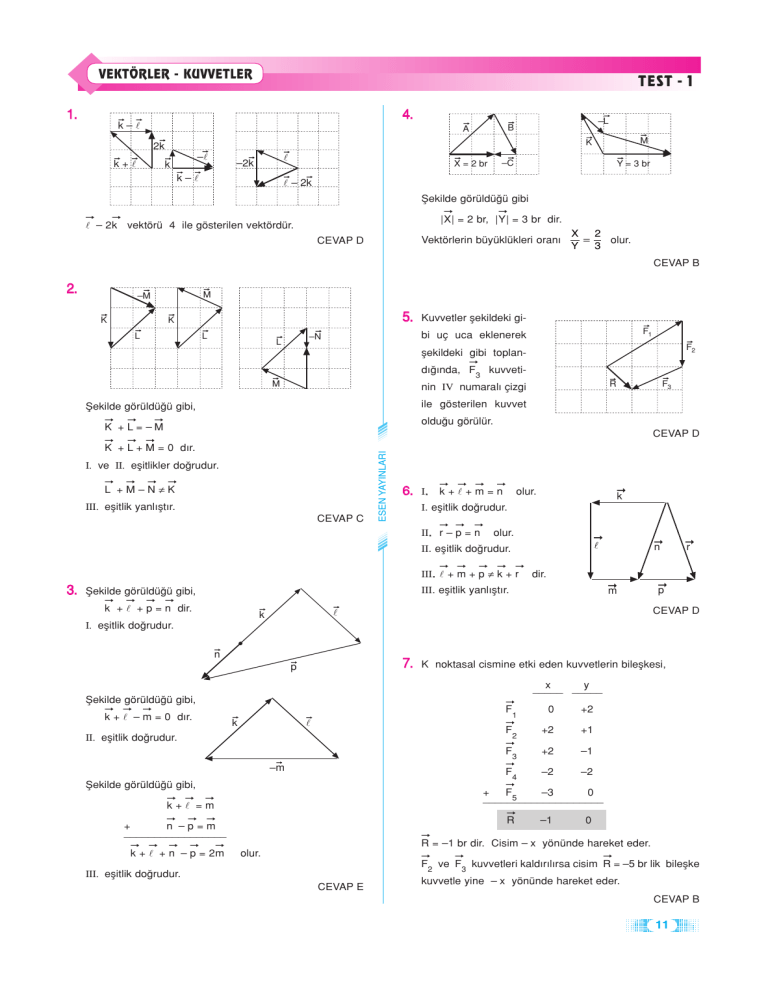
VEKTÖRLER - KUVVETLER
1.
TEST - 1
4.
k–l
M
K
2k
k+l
–L
B
A
–l
k
l
–2k
k–l
X = 2 br
–C
Y = 3 br
l – 2k
fiekilde görüldü¤ü gibi
➞
➞
➞
➞
| X| = 2 br, | Y| = 3 br dir.
l – 2 k vektörü 4 ile gösterilen vektördür.
Vektörlerin büyüklükleri oran›
CEVAP D
X 2
olur.
=
Y
3
CEVAP B
2.
M
–M
K
5.
K
L
L
F1
bi uç uca eklenerek
–N
L
Kuvvetler flekildeki giF2
flekildeki gibi toplan➞
d›¤›nda, F3 kuvvetiM
ile gösterilen kuvvet
fiekilde görüldü¤ü gibi,
➞
➞
➞
oldu¤u görülür.
K +L= –M
➞
CEVAP D
➞
K + L + M = 0 d›r.
I. ve II. eflitlikler do¤rudur.
➞
➞
➞
➞
L +M–N≠K
III. eflitlik yanl›flt›r.
CEVAP C
ESEN YAYINLARI
➞
F3
R
nin IV numaral› çizgi
6.
➞
I..
➞
➞
➞
k+l+m=n
olur.
k
I. eflitlik do¤rudur.
➞
➞
➞
II.. r – p = n
olur.
n
II. eflitlik do¤rudur.
➞
➞
➞
➞
➞
III.. l + m + p ≠ k + r
3.
➞
➞
➞
dir.
III. eflitlik yanl›flt›r.
fiekilde görüldü¤ü gibi,
r
m
p
➞
k + l + p = n dir.
l
k
CEVAP D
I. eflitlik do¤rudur.
n
7.
p
K noktasal cismine etki eden kuvvetlerin bileflkesi,
x
y
_____
_____
fiekilde görüldü¤ü gibi,
➞
➞
➞
➞
k + l – m = 0 d›r.
l
k
F1
0
+2
F2
+2
+1
F
+2
–1
–2
–2
➞
II. eflitlik do¤rudur.
➞
3
➞
–m
F4
fiekilde görüldü¤ü gibi,
➞
➞
➞
+
F5
–3
0
____________________
➞
k+l =m
➞
➞
➞
➞
R
+
n –p=m
_________________
➞
➞
➞
➞
0
R = –1 br dir. Cisim – x yönünde hareket eder.
➞
k + l + n – p = 2m
–1
➞
olur.
➞
➞
➞
F ve F kuvvetleri kald›r›l›rsa cisim R = –5 br lik bileflke
2
III. eflitlik do¤rudur.
CEVAP E
3
kuvvetle yine – x yönünde hareket eder.
CEVAP B
11
Vektörler - Kuvvetler
8.
11.
x
y
_____
_____
:
1
2
F2 :
2
–1
1
II
F1
➞
F
➞
F2 + F3
➞
+
F3 : –1
–1
____________________
➞
➞
F2 + F3
IV
R
➞
F1 + F2 + F3 : 2
0
➞
➞
➞
➞
R = F1 + F2 + F3
1
2
F3 :
–1
–1
➞
olur.
x
y
_____
_____
➞
➞
F1 :
➞
oldu¤una göre F2 + F3 flekildeki gibi
➞
II ve IV numaral› kuvvetlerin bileflkesi F + F bileflke2
3
sine eflittir.
➞
CEVAP B
➞
+
F4 :
3
1
____________________
➞
➞
➞
F1 + F3 + F4 : 3
2
x
y
_____
_____
➞
F3 :
–1
–1
➞
+
F4 :
3
1
____________________
➞
F3 + F4 : 2
➞
➞
k vektörü ile l vektörünün
bileflkesi m vektörü oldu¤u-
0
➞
na göre m vektörünün yatay
➞
Bu durumda I ve III vektörleri F vektörüne eflittir.
CEVAP E
➞
bilefleni mx = 9 br, düfley bi➞
➞
➞
➞
m› +x yönünde IRI = 27 br
–k = 12
➞
➞
➞
➞
2l = 18
➞
m – k + 2l vektörünün topla-
➞
➞
m–k=l
fiekilde görüldü¤ü gibi
➞
k + l + m = – 4 k d›r.
mx = 9
•
lefleni ise my = 12 br olur.
olur.
9.
m y = 12
➞
ESEN YAYINLARI
➞
12.
➞
k+l
➞
➞
➞
m – k + 2l = 3l
k+m
➞
➞
➞
m
–k
3l = 3.9 = 27 br
–k
.
k + l + m = –4k
➞
l
CEVAP A
CEVAP C
10. P
cismi x do¤rultu-
sunda hareket etti¤ine
➞
göre, F3 kuvvetinin y
F2
F1
bilefleni –1 br olmal›d›r.
Buna göre,
II. yarg›
P
x
kesin do¤rudur.
I. ve III. yarg›lar için kesin birfley söylenemez.
CEVAP B
12
VEKTÖRLER - KUVVETLER
1.
TEST - 2
l
5.
k
l
k
m
k+m
k+l
l+m
➞
➞
➞
➞
➞
L
m
M
N
—
2
➞
Ik + lI ≠ I l + mI
I. ifade yanl›flt›r.
➞
➞
➞
I..
II. ifade do¤rudur. Ik + mI < I k + lI
➞
➞
➞
➞
III. ifade yanl›flt›r. 2I k + mI ≠ I lI
➞
N
= 0 olur.
2
L+M+
➞
II.. K ≠ 2N
➞
CEVAP B
➞
➞
➞
III.. IK – NI = 6 br, IL – MI = 5 br oldu¤undan III. ifade
yanl›flt›r.
CEVAP A
2.
F3
2F1 – F2
6.
F2
– F2
➞
➞
➞
➞
R=K+L+M
M
➞
R
oldu¤una göre M vektörü,
R
L
K
F1
2F1
➞
➞
➞
➞
2F1 – F2 ve 2F1 vektörleri kullanarak – F2 vektörünü
flekildeki gibi buluruz.
➞
➞
➞
➞
Bileflke vektör; R = F1 + F2 + F3
olup 2 yönündedir.
ESEN YAYINLARI
I ile gösterilen vektördür.
CEVAP A
CEVAP B
7.
➞
➞
➞
➞
F1, F2, F3 ve F4 ün bilefl-
F1
kesi +x yönünde 1 br olur.
3.
➞
➞
➞
Cismin y do¤rultusunda ha-
➞
F1 + F2 + F3 + F4 = 0 dir.
➞
➞
➞
➞
➞
reket edebilmesi için II ve-
F2
F1
K R
F2
F3
ya III kuvvetleri uygulan-
➞
F1 + F2 + F3 + F4 + F5 = F5
F4
mal›d›r.
F5
CEVAP E
olur.
F3
F4
CEVAP E
8.
➞
Bileflke vektör: R
➞
4.
➞
➞
➞
➞
➞
➞
➞
➞
➞
➞
➞
➞
➞
R = (a + 2b) + (a – 2b) + c
➞
a + b = (K + L + M) + (–K – M + 2L) = 3L
➞
a – 2b
a + 2b
➞
a + b 3L
=
= L olaca¤›ndan 3 vektörüdür.
3
3
c
➞
= 2a + c
R
➞
2a + c vektörü II numaral› vektördür.
CEVAP C
CEVAP B
13
Vektörler - Kuvvetler
9.
➞
➞
➞
12.a + d vektörü –b
Cismin dengede kalmas› için
II
bileflke kuvvet s›f›r olmal›d›r.
vektörüne
eflittir.
IV
a
I. eflitlik do¤rudur.
II ve IV kuvvetlerinin bilefl➞
d
K
kesi F kuvvetine eflit ve z›t
–F
a+d
yöndedir.
➞
CEVAP E
➞
➞
➞
a + e vektörü b + c vektörünün tersine eflittir. II. eflitlik
yanl›flt›r.
➞
➞
➞
a
e
➞
–e – b = a + c
➞
➞
➞
a+e
➞
–b – c = a + e
➞
➞
➞
oldu¤undan III. eflitlik do¤rudur.
10. Düfley
üç bölme oldu-
F2 = 6N
➞
¤undan F = 6N veril2
di¤inden düfley bir bölme
2N
F3y = 4N
al›nd›¤›nda,
➞
kuvvetinin düfleyi
F1 = 5N
4N, yatay› ise 5N olur.
F3x = 5N
Bu durumda bileflke
kuvvet 10 2 N olur.
R = 10 2N
10N
Cismin hareketsiz kalmas› için 3 yönünde
10 2 N luk kuvvet uy-
45°
45°
gulanmal›d›r.
10N
CEVAP D
11. Bileflke kuvvet
➞
➞
R, F ile ayn›
➞
F5
5
do¤rultudad›r. F5 kuvveti kal-
F1
R
d›r›l›nca K cisminin hareket
K
yönü de¤iflmez.
F4
F2
F3
CEVAP E
14
ESEN YAYINLARI
F3
b+c
➞
– (b + c) = a + e
b
c
CEVAP D
VEKTÖRLER - KUVVETLER
1.
TEST - 3
Kuvvetleri eflkenar üçgenin
4.
3f
➞
Bileflke vektör: R
➞
merkezinde gösterelim.
➞
➞
➞
➞
F1
R = F1 + F2 + F3 + F4 olur.
f
➞
O
Bileflke kuvvet, F2 ile F3
120°
F2
➞
F4
kuvvetlerinin bileflkesi ile
R
ayn› yöndedir.
F3
4f
5f
4f ile 4f aras›ndaki aç› 120° dir.
3f
Bu iki kuvvetin bileflkesi 4f dir.
CEVAP B
4f ile 3f z›t yönde ve bileflke
O
4f – 3f = f olur.
120°
4f
5f – f = 4f
4f
5.
➞
➞
CEVAP A
➞
➞
K + N + P = 0 olur.
➞
K
➞
L + M = – P dir.
P
Buna göre,
➞
➞
➞
➞
➞
➞
K + N + P + L + M = –P
2.
olur.
l
s
k
➞
➞
➞
➞
➞
➞
ESEN YAYINLARI
r
m
n
N
p
L
M
CEVAP B
k + l + m = 0 olur.
p + r + s = 0 olur.
➞
➞
➞
➞
➞
➞
➞
➞
k + l + m + n + p + r + s = n dir.
➞
Bu bileflke vektörün s›f›r olmas› için eflitli¤in soluna – n
6.
➞
➞
Duran m kütleli cisme F1 , F2
F2
ile birlikte III numaral› kuvvet
vektörü eklenmelidir.
etki ederse cisim –y yönünde
CEVAP D
hareket eder.
F1
m
III
R
y
3.
d2
F
CEVAP C
F2
d1
F1
K
Bu tür sorularda paralel kenar çizilir. fiekilde görüldü¤ü gibi
➞
➞
7.
Rmax = 4 + 5 + 11 = 20 N
➞
F1 ile F2’nin bileflkesi F olmaktad›r. Bu durumda
Rmin = 11 – 5 – 4 = 2 N olur.
IF2I > IF1I = IFI olur.
Rmax 20
=
= 10 olur.
Rmin
2
➞
➞
➞
CEVAP E
CEVAP D
15
Vektörler - Kuvvetler
8.
➞
➞
➞
11. F1 , F2 , F3
P cismine etki eden befl
➞
kuvvetin bileflkesi R dir.
kuvvetlerine
I numaral› kuvvet ekle-
➞
min hareket yönü de¤ifl-
➞
F5
P R
F5 kuvveti kald›r›l›nca cis-
nirse bileflke kuvvet R
F3
olur.
F1
F4
F1
F2
mez.
F2
F3
cisim
I
R
CEVAP E
CEVAP A
9.
1 nolu kuvvet kullan›ld›¤›nda
12.
L
y
cisim L noktas›ndan geçer.
F3
F3y
K
1
F1
F1y
F3
α
F1
α
θ
CEVAP A
•
x
F1x
F3x
ESEN YAYINLARI
F2
θ
F2
Cisim sabit h›zla hareket etti¤ine göre,
➞
➞
➞
F + F + F = 0 olur.
1
2
3
III. eflitlik do¤rudur.
➞
➞
➞
2
= 2 2 f.
2
= 2f
➞
➞
I T I = I TI . cos60°
y
= 4f.
1
2
Fy
➞
➞
F1 ile F3 aras›ndaki aç› 90° oldu¤undan α + θ = 90° dir.
2f
➞
45°
Tx
➞
= I F I.sinθ + I F I.sinα olur.
1
3
F = 2 2f
•
F
2
kuvveti ayn› zamanda,
➞
Fx
60°
•
x
➞
➞
F2 = I F 1 I.cosα + I F 3 I.cosθ olur.
Ty
I. eflitlik do¤rudur.
T = 4f
➞
➞
IF 1 I = IF 3 I
x
➞
I T x I = I TI . sin60°
II. eflitlik do¤rudur.
3
2
CEVAP E
2f
2f
x
2f
2 3f
fiekildeki befl kuvvetin
x
➞
I F 1 I.cosθ = I F 3 I.cosα olur.
y
= 2 3f
2f
bileflkesi 2 3 f olur.
CEVAP C
16
y
➞
➞
= 4f.
➞
y
y
= 2f
➞
➞
IF I = IF I + IF I
2
1
3
➞
10. IF x I = IF y I = IFI . cos45°
VEKTÖRLER - KUVVETLER
1.
TEST - 4
➞➞➞
a, b, c vektörlerinin fliddet-
5.
K
M=a
•
ki aç› 120° oldu¤undan K
a
s›ndaki aç› 120° dir.
➞
➞
➞
leri eflittir. Bu vektörler ara-
➞
➞
K ile M vektörleri aras›nda-
➞
➞
30°
K=a
ile M nin toplam› a d›r.
L
➞
Buna göre, a + b + c = 0
120°
olur.
120°
60°
120°
fiekildeki üçgenden,
b
L
•
c
30°
R
sin 30° = a
1
R
= a
2
M
CEVAP A
K+M=a
R=
(
L
a
2
•
R
olur.
CEVAP C
2.
Üç vektörün bileflkesi s›f›rd›r.
➞
➞
➞
A + B + C = 0 d›r.
A
C
I. eflitlik kesinlikle do¤rudur.
•
Vektörler flekildeki gibi dik üçgenin
B
kenarlar› olsayd›,
➞
➞
2
➞
2
6.
2
y
y
IAI = IBI + ICI do¤ru olurdu.
için kesin birfley söylenemez.
R
di¤imiz için III. eflitlik için kesin birfley söylenemez.
CEVAP A
3.
➞
➞
➞
➞
➞
➞
F2
fiekil - I de bileflke vektör F1 e yak›n oldu¤u için
➞
fiekil - II de bileflke vektör F e yak›n oldu¤u için
3
x
y
_____
_____
F3 > F1 dir.
➞
3
Bu durumda kuvvetlerin büyüklükleri aras›nda,
➞
F > F > F iliflkisi vard›r.
3
1
2
+
M
1
–1
____________________
CEVAP D
➞
X–Y
➞
fiekil - II
➞
F1 > F2 dir.
–1
x
R
F3
fiekil - I
➞
K
60°
30°
60°
x
K
=K+M
➞
60°
30°
X – Y= K + L– L+ M
➞
60°
30
➞
ESEN YAYINLARI
➞
IBI + ICI = IAI olur. Fakat vektörlerin konumunu bilme-
°
K
Vektörler bir do¤ru üzerinde olsayd›,
➞
F1
F1
Vektörlerin bu flekilde oldu¤unu bilmedi¤imiz için II. eflitlik
0
2
➞
X–Y
bileflke vektörünün koordinatlar›
2
(0, 1) olur. Bu vektör, I numaral› vektördür.
oldu¤una göre,
CEVAP A
7.
➞ ➞
α = θ oldu¤u için;
k
➞
A
k
l
➞
l
Ak
= 1 dir.
Al
➞
K – 2M
➞
•
➞
I A I = I A I olur.
2K + L
•
4.
➞
3K
Ak
α θ
➞
–(L – 2M)
➞
Al
➞
➞
➞
➞
➞
➞
(2K + L) – (L – 2M) + (K – 2M) = 3K olur.
➞
➞
I3KI = 6 br ise K nin büyüklü¤ü 2 br olur.
CEVAP D
CEVAP C
17
Vektörler - Kuvvetler
8.
11.
F2
kuzey
F1
F
F2 + F3 = – —–1
2
K
K
bat›
•
F2
.
do¤u
45°
F3
➞
➞
➞
➞
F
⇒ F2 + F3 = – —1
2
➞
➞
➞
F
F1 + F2 + F3 = —1
2
dir.
F1
Bileflke kuvvet s›f›r olursa K cismi sabit h›zla hareket eder.
güney
➞
I.
F1 kuvvetinin fliddeti yar›ya inerse bileflke kuvvet s›f›r
olur.
➞
➞
olabilir.
➞
➞
➞
I. yarg› yanl›flt›r.
➞
F4 ün yönü kuzey-bat›ya do¤rudur.
➞
III. F ile F fliddeti iki kat›na ç›karsa, 2(F + F ) = –F olur.
2
3
➞
2
➞
3
II. yarg› yanl›flt›r.
1
➞
F + 2F + 2F = 0 olur.
1
➞
I F 4 I > I F 3 I olur.
➞
II. α aç›s› azalt›l›rsa F2 + F3 fliddeti artar ve bileflke s›f›r
➞
F3
F4
2
➞
3
➞
➞
➞
I F 1 + F 2 + F 3 I = I F 4 I olur.
CEVAP E
III. yarg› do¤rudur.
ESEN YAYINLARI
CEVAP C
9.
K–L
K
–L
K
P
12.
➞
L
III
II
IV
➞
M
L
➞
➞
➞
➞
➞
K + L + P = 0 oldu¤una göre P , V numaral› vektördür.
CEVAP E
➞
θ
θ
α
α
➞
➞
K
I
➞
K + L bileflkesi I. bölgede ise I KI > I LI olur.
➞
➞
➞
➞
M + L bileflkesi III. bölgede ise I LI > I MI olur.
Vektörlerin büyüklükleri aras›ndaki iliflki K > L > M olur.
CEVAP B
10.
X
2X
–Z
–M
X
Y
L
K
L
K
➞
➞
➞
K =
X+Y
➞
➞
L =
X–Z
➞
➞
➞
➞
+ mM=mY!Z
________________
➞
➞
➞
➞
M vektörü (–) ile çarp›l›rsa
➞
K + L – M = 2X
Buna göre, Z > X > Y olur.
CEVAP B
18
VEKTÖRLER - KUVVETLER
1.
➞
TEST - 5
➞
A ve B vektörleri aras›n-
4.
y
daki aç› 90° dir.
➞
➞
➞
➞
➞
➞
A + B = 0 ise Ax = – Bx ve IAI = IBI olur.
I ve III ifadeleri do¤rudur.
CEVAP D
A
B
•
x
CEVAP D
5.
fiekildeki üçgenden
R = 6N
R
cos 30° =
F2
2.
3
6
=
2
F2
12
= 4 3N
F2 =
3
➞
Befl kuvvetin bileflkesi R
➞
➞
F1
R
dir. R kuvveti F1 ile ayn›
M
F2
do¤rultudad›r.
30°
•
F1
bulunur.
CEVAP C
F3
F5
F4
F2
3.
fiekil - I için
1N
1N
120°
2N
1N
1N
1N
60°
120°
60°
120°
2N
|F1|= 3N
ESEN YAYINLARI
CEVAP A
6.
➞
➞
➞
I K + L + MI = 2 N
y
+y yönünde ise
➞
➞
L
K
I K + LI = 6 N +y
yönünde olmal›d›r.
30°
2α + α = 90°
60° 60°
30°
x
α = 30° olur.
1N
2N
➞
➞
IMI = 4N
I KI = I LI ≠ 2 N
I. eflitlik yanl›flt›r.
fiekil - II için
➞
➞
I KI = I LI = 6 N olur.
5N
1N
5N
5N
120°
1N
|F2|= 3N
➞
1N
60°
➞
II. eflitlik do¤rudur.
60°
1N
➞
I M – K – LI = 4 + 6 = 10 N olur.
➞
➞
I L . cosαI ≠ I K . sinαI olur.
4N
III. eflitlik yanl›flt›r.
4N
CEVAP B
fiekil - III için
8N
7N
7N
60°
1N
120°
1N
8N
1N
1N
7.
➞
➞
olur.
|F3|= 3N
➞
➞
➞
➞
a – b + c = (2c) + c = 3c
➞
➞
➞
a – b + c vektörünün bü-
8N
Görüldü¤ü gibi aralar›nda 120° aç› olacak flekilde kesiflen
3c = 60
c = 20 br olur.
1N, 2N, 3N veya 4N, 5N, 6N
.......... n, n + 1, n + 2 fleklinde olan vektörlerin bileflkesi
➞
her zaman |R| = v3 N olur.
CEVAP A
–b
a
yüklü¤ü 60 br oldu¤undan,
θ
c
c
θ
a – b
CEVAP B
19
Vektörler - Kuvvetler
8.
➞
➞
➞
➞
➞
➞
11. K
➞
F1
F1 + F2 + F3 = 0 d›r.
➞
➞
F3
I. yarg› do¤rudur.
➞
➞
L
numaral› kuvvet uygu-
olur.
➞
➞
kuvvetleriyle birlikte II
– F + F + F = –2F
1
2
3
1
➞
➞
cismine F1 , F2 , F3
R
F2
lan›rsa cisim L noktaII
s›ndan geçer.
➞
K
F1 – F2 – F3 = 2F1 olur.
II. yarg› do¤rudur.
➞
➞
➞
➞
F2
➞
F1
F3
– F1 – F2 + F3 = 2F3 olur.
CEVAP B
III. yarg› do¤rudur.
CEVAP E
➞
➞
➞
➞
12. K
S+T–L=K
oldu¤undan I. eflitlik
do¤rudur.
➞
➞
K
➞
P
➞
➞
➞
➞
➞
F2
➞
➞
L
➞
➞
olur.
T
II. eflitlik do¤rudur.
➞
➞
F3
F1 + F2 + F3 + F4 = 0
M
➞
➞
–P – S = – K olur.
➞
➞
➞
S
L+M=–K
➞
➞
➞
➞
cismi sabit h›zla hare-
ket etti¤ine göre,
➞
➞
K + L + M ≠ S + P + T dir.
III. eflitlik yanl›flt›r.
CEVAP C
ESEN YAYINLARI
9.
K
F1 kuvveti ters çevrilirse,
cisim yavafllar durur ve
➞
–F1 yönünde h›zlan›r.
➞
F1
I. yarg› do¤rudur.
➞
F4
➞
Cisim F2 yönünde hareket etmez.
II. yarg› yanl›flt›r.
➞
Bileflke kuvvetin fliddeti 2I F1 I olur.
III. yarg› do¤rudur.
CEVAP D
➞
10.F3
➞
ile F1 in bileflke-
sinin fliddeti,
50 – 20 = 30 N olur.
IF2I = 40N
IF3 + F1I = 30N
Aradaki aç› 90°
α
oldu¤unda,
K
R2 = (30)2 + (40)2
R = 50 N olur.
➞
➞
➞
➞
0° < α < 90° oldu¤u için F + F + F bileflke fliddeti R,
1
2
3
➞
50 > I RI > (40 + 30)
➞
50 > I RI > 70 olur.
➞
I RI = 60 olabilir.
CEVAP C
20
VEKTÖRLER - KUVVETLER
1.
TEST - 6
➞
5.
C vektörü II ve III
B
kesikli çizgileri oldu➞
C
A
‹lk durumda cismin üzerine uygulanan net kuvvet,
➞
➞
¤unda B + C bilefl-
➞
➞
➞
F1
➞
➞
F2
R1 = F1 + F2 + F3 = 2 br
➞
kesi A vektörüne dik
B+C
olur.
•
–x yönünde 2 birimdir.
C
•
➞
K
F1 kuvveti kald›r›d›¤›nda uygulanan net kuvvet;
B+C
➞
B
➞
➞
R2 = F2 + F3 = 2 br
➞
–y yönünde 2 birim olur. Kuv-
CEVAP D
F3
vetin büyüklü¤ü de¤iflmede➞
2.
➞
➞
I F1 I > I F2 I > I F3 I ise
y
büyük kuvvet karfl›s›nda küçük aç›,
Cismin hareket yönü de¤iflir. ‹lk durumda –x yönünde,
ikinci durumda –y yönünde gider.
F1
küçük
➞
¤inden ( |R | = |R | ) ivme ve h›z›n büyüklü¤ü de¤iflmez.
1
2
➞
CEVAP A
kuvvet karfl›s›nda büyük aç› olmal›d›r.
➞
α
➞
x
2α
F II nolu, F III nolu
2
3
kuvvetler olabilir.
F3
F2
CEVAP D
3.
➞
6.
ESEN YAYINLARI
1
F2
2
0
F3
1
–3
➞
➞
d
d+e =f
➞
–2
➞
➞
x
y
_____
_____
F1
➞
a+b+c =0
➞
➞
➞
➞
➞
➞
➞
➞
e
f
h+l =g
l
a
f =g
b
h
Buna göre, tüm vektör➞
lerin toplam›
➞
+
F4
–1
–2
____________________
4f
olur.
g
c
I f I = 4 br oldu¤una gö➞
➞
R
0
re 4f = 16 br olur.
–4
CEVAP E
Cisim – y yönünde hareket eder.
➞
➞
➞
F3 ve F4 kuvvetlerinin bileflkesi y do¤rultusunda, F1 ile
➞
F2 kuvvetlerinin bileflkesi de y do¤rultusundad›r.
➞
➞
Bu durumda, F ve F seçeneklerde olmad›¤›ndan Cevap
3
4
A d›r.
CEVAP A
4.
7.
K
R
80°
K
L
70°
30°
•
30°
70°
L
fiekil - I
fiekil - II
➞
L
K vektörünü fiekil - II deki gibi parelel tafl›yacak olursak
vektörlerin karfl›lar›ndaki aç›lar;
–M
➞
IK + LI = 3IMI oldu¤undan I. yarg› do¤rudur.
80°
L
L–M
K+L
80° K
R
K
K ile L – M vektörleri birbirlerine diktir. III. yarg› do¤rudur.
➞
➞
R → 70° , K → 30° , L → 80° olur.
Büyük aç›n›n karfl›s›ndaki vektör büyük olaca¤›ndan,
➞
➞
➞
I LI > I RI > I KI olur.
Bu durumda verilen her üç ifade de do¤ru olur.
K ≠ 2M oldu¤undan II. yarg› yanl›flt›r.
CEVAP D
CEVAP E
21
Vektörler - Kuvvetler
8.
➞
➞
➞
➞
➞
11.
K = a + b + c = 2c ise,
l
➞
I KI =20 cm olur.
➞
➞
➞
I LI = a – b
➞
10
I LI = 2 (5 3 ) cm dir.
20
2 3
=
=
3
2 (5 3 )
ILI
60°
Al
5 3
20°
30°
b
IKI
130°
A
a
5
30°
k
Ak
•
c
Büyük aç› karfl›s›nda büyük kenar, küçük aç› karfl›s›nda
olur.
küçük kenar vard›r.
CEVAP B
Buna göre, A > A > A olur.
k
l
CEVAP C
9.
➞
➞
12. IMI
= IKI. cos 60°
l
1
2
= 15 br
= 30 .
k
•
m
m
R1 = k + l
R3 = l + m
R2 = k + m
Aç› büyüdükçe bileflke vektörün fliddeti azal›r.
➞
➞
➞
I R I > I R I > I R I olur.
1
2
3
CEVAP A
10.
y
10N
y›
10N
8N
6N
x›
53°
37°
53°
x
37°
16°
8N
6N
x - y koordinat düzlemi ok yönünde 16° döndürülünce
flekildeki gibi yatay bileflen 8 N, düfley bileflen 6 N olur.
CEVAP B
22
L
IKI=30br
Uç uca ekleme metodu-
R3
120°
l
30°
150°
➞
ESEN YAYINLARI
R1
k
R2
➞
➞
na göre K + L = 2M dir.
Öyleyse bileflke vektör
➞
➞
➞
➞
60°
•
➞
M
R = K + L + M = 3.M = 3.15 = 45 br dir.
CEVAP C