final sınavının konuları - Dokuz Eylül Üniversitesi

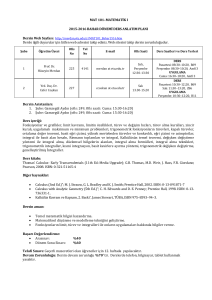
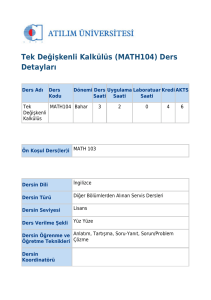
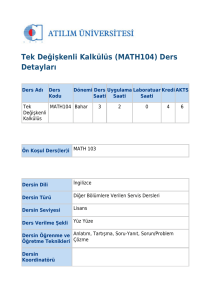
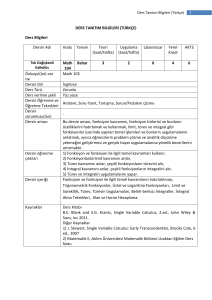
MAT1009 MATEMATİK I
05.01.2010
Dokuz Eylül Üniversitesi Fen-Edebiyat Fakültesi Matematik Bölümü
Öğretim Üyesi: Engin Mermut
FİNAL SINAVININ KONULARI
Öğretim Üyesi: Engin Mermut
e-posta: engin.mermut@deu.edu.tr
Tel: (232) 412 85 82
web: http://kisi.deu.edu.tr/engin.mermut/
Asistan: Buğurcan Rüzgar
Tel: (232) 412 285 69
DERSİN WEB SAYFASI:
http://kisi.deu.edu.tr/engin.mermut/MAT100-Matematik-I-Jeoloji_2009g.html
•
Ders kitabı: Kalkülüs: Kavram ve Kapsam, Diferansiyel ve Integral Hesap, James Stewart, 2001,
Brooks/Cole, ikinci baskı, Türkçe çevirisi TÜBA Yayınları, 2007.
•
FİNAL SINAVINIZIN KONULARI, limit, türev ve integraldir (ve tabi zaten bunlar
icin gerekli olan temel önbilgiler, fonksiyonlar ile ilgili temel bilgilerdir). Ders kitabınızın ilk altı bölümündeki (ve eklerindeki) aşağıdaki konulardan finalde sorumlusunuz. Önbilgiler ve fonksiyonlarla ilgili
giriş konularını geçersek, esas olarak final sınavınızda limit, türev, integral ve türev ve integralin uygulamalarından sorular olacaktır. Limit, türev ve integral hesapları, optimizasyon
problemleri, bir fonksiyonun grafiğinin türev yardımı ile çizimi, eğrilerle sınırlı bölgelerin
alanını bulma, cisimlerin hacimlerini bulma, eğrilerin uzunluğunu bulma final sınavınızda
karşılacağınız ana konulardır.
• Önbilgiler: Temel cebir, geometri ve trigonometri formulleri; Gerçel (reel) sayılar; Karmaşık sayılar (Kompleks sayılar), karmaşık sayıların kutupsal biçimi, De Moivre teoremi, karmaşık sayıların
kökleri, karmaşık üsteller; Aralıklar, eşitsizlikler ve mutlak değer; Koordinat Geometrisi, doğrular,
paralel ve dik doğrular, çemberler, konik kesitler, paraboller, elipsler, hiperboller; Trigonometri,
açılar, trigonometrik fonksiyonlar,Ptrigonometrik özdeşlikler, trigonometrik ve ters trigonometrik
fonksiyonların grafikleri; sigma ( ) gösterimi; Kutupsal koordinatlar, kutupsal koordinatlarda
eğriler.
−→ Ekler A, B, C, F, H.1, I.
• Fonksiyonlar ve Modeller: Bir fonksiyonun dört farklı gösterimi; Matematiksel modeller; Eski
fonksiyonlardan yeni fonksiyonlar elde etme; Grafik çizen hesap makineleri ve bilgisayarlar; Üstel
fonksiyonlar; Ters fonksiyonlar ve logaritma; Parametrik eğriler.
−→ Bölüm 1’in tümü (kısım 1.4 hariç).
• Limit ve Türevler: Teğet ve hız problemleri; Bir fonksiyonun limiti; Limit kuralları ile limit
alma; Süreklilik; Sonsuzluk içeren limitler; Limitlerin kesin tanımları; Teğet, hız ve diğer değişim
hızları; Türevler; Bir fonksiyon olarak türev; Doğrusal yaklaştırımlar; f nin türevi f hakkında ne
söyler?; Kutupsal eğrilere teğetler; Fermat teoreminin kanıtı.
−→ Bölüm 2’nin tümü ve Ekler D, E, H.1.
• Türev alma kuralları: Polinomların ve üstel fonksiyonların türevleri; Çarpım ve bölüm kuralları; Doğal ve sosyal bilimlerde değişim hızları; Trigonometrik fonksiyonların türevleri; Zincir
kuralı; Kapalı fonksiyonların türevi; Logaritma fonksiyonlarının türevleri; Doğrusal yaklaştırımlar
ve diferansiyeller.
−→ Bölüm 3’ün tümü.
• Türevin uygulamaları: Bağımlı hızlar; Maksimum ve minimum değerler; Türev ve eğrilerin
biçimi; Belirsizlik durumları ve L’Hospital Kuralı; Optimizasyon problemleri; Newton yöntemi;
İlkeller.
−→ Bölüm 4’ün tümü (kısım 4.4 ve 4.7 hariç).
• İntegral: Alanlar ve uzaklıklar; Belirli integral; Belirli integrallerin hesabı; Kalkülüsün temel
teoremi; Yerine koyma kuralı; Kısmi integral alma; Diğer integral alma teknikleri; Trigonometrik
integraller; Trigonometrik değişken değiştirme; Rasyonel fonksiyonların kısmi kesirlerle integralini
alma; Has olmayan integraller.
−→ Bölüm 5’in tümü (kısım 5.8 ve 5.9 hariç) ve Ek G.
• İntegralin Uygulamaları: Alanlar hakkında ek bilgi; Hacimler; Yay uzunluğu; Kutupsal koordinatlar, kutupsal koordinatlarda eğriler; Kutupsal eğrilere teğetler; Kutupsal koordinatlarda alan
ve uzunluk; Bir fonksiyonun ortalama değeri.
−→ Bölüm 6’nın tümü (kısım 6.5, 6.6 ve 6.7 hariç) ve Ekler H.1, H.2.