BLM441 örnek sorular ve çözümleri. 1. (2009 final sınavından) 2

BLM441 örnek sorular ve çözümleri.
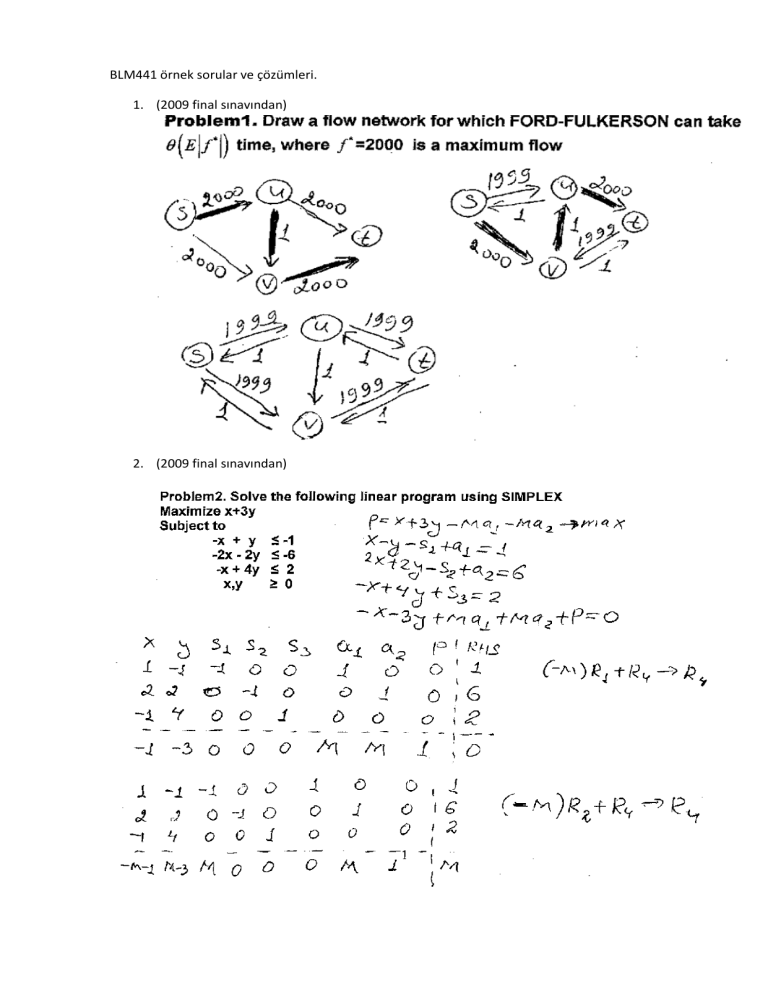
1. (2009 final sınavından)
2. (2009 final sınavından)
Soru3.(2009 final sınavından)
Soru4. (2009 arasınav2 den)
Soru5. (2009 arasınav 2 den)
Soru6. (2010 final sınavından)
1
3
x
3
x
x
2
1
6
2
x
x
2
x
1
Yukarıdaki şekilde içinde x olmayan karelere pozitif tam sayılar yazılmıştır.
Şekildeki her kareden bu kareyle ortak kenarı veya ortak köşesi olan her kareye gidilebilir ve gidişin
bedeli karelerin içindeki sayıların toplamına eşittir. İçinde x yazılan karelere gidilemez ve bu karelerden
çıkış yoktur. Sol üst köşeden sağ alt köşeye en az bedelle gelinmesi isteniyor. Karelerin içindeki sayılar
ne olursa olsun( pozitif tam sayılar olmak koşuluyla) bu soruyu çözen bir algoritma yazınız ve
algoritmanızın çalıştığını yukarıdaki veriler üzerinde gösteriniz.
Çözüm.
a
4
4
4
3
4
e
3
h
c
5
3
d
b
8
9
7
5
f
7
8
3
i
g
Soruyu Dijkstra algoritması çözüyor.
Örnek üzerinde açıklaması:
adım
1
2
3
4
5
6
7
8
9
a
0
b
∞
4
4
Soru7 (2010 final)
c
∞
∞
∞
∞
10
10
d
∞
3
e
∞
∞
6
6
f
∞
∞
∞
∞
13
13
13
g
∞
∞
∞
∞
∞
∞
15
15
h
∞
∞
7
7
7
i
∞
∞
∞
∞
∞
∞
∞
20
18
Soru8(2010 final)
Soru9 (2010 final)
Soru10. (2011 final) Aşağıdaki doğrusal programlama sorusunu Simpleks yöntemle çözünüz.
3 x1
2 x2
x1
2 x2
x1
x2
x1
0, x 2
x3
max
10
x3
12
0, x3
0
Çözüm.
x1
x2
x3
s1 s 2 P RHS
s1 1
2
0
1 0
0 10
s2 1
1
1
0
1
0 12
P 3
2
1
0
0
1 0
10:1=10 min
12:1=12
s1 çıkan x1 giren değişken
R1
3R1
R2
R3
R2
R3
x1
x2
x3
s1 s 2 P RHS
x1 1
2
0
1 0
0 10
s2 1
1
1
1 1
0 2
P 0
4
1
3
1 30
0
2:1=2 min
s 2 çıkan x 3 giren değişken
x1
x2
x3
s1 s 2 P RHS
x1 1
2
0
1 0
0 10
x3 0
1
1
1 1
0 2
0
2
P 0
x1
3
10, x 2
1 1 32
2 ve en büyük değer 32 bulundu.
0, x3
Soru1 2. (2011 final)
x1
2 x2
3 x3
x1
2 x3
7
2 x1
x2
x3
3x2
2 x3
5
0, x 2
0
x1
max
2
doğrusal programlama sorusu veriliyor.
a) Soruyu standart biçime dönüştürmeden sorunun eşleniğini yazınız.
b) Soruyu Büyük M yöntemi ile çözülebilecek biçime dönüştürünüz.
Çözüm. a)
7 y1
y1
2 y2
2 y2
y2
5 y3
min
1
3 y3
2
2 y1
y2
2 y3
y2
0, y 3
0
3
b)
x1
2 x2
3 x3
3x 4
x1
2 x3
2 x4
a1
2 x1
x2
x3
3x 2
2 x3
x1
0, x 2
0, x3
Ma2
max
7
x4
2 x4
Ma1
s1
s2
a2
2
5
0, x 4
0, a1
0, a 2
0, s1
0, s 2
0
Soru13. (2011 final) Bir evlilik programına katılan 5 erkek (A, B, C, D ve E) ve 5 kadının (X,
Y, Z, W, V ) her birinin sıralı tercih listesi aşağıdaki gibidir:
A nın tercih listesi: X, Y, Z, W, V
B nin tercih listesi
X, Z, Y, V, W
C nin tercih listesi
Y, Z, X, V, W
D nin tercih listesi
W, Y, Z, X, V
E nin tercih lsitesi
Y, X, W, Z, V
X in tercih listesi
D, B, A, E, C
Y nin tercih listesi
A, B, C, D, E
Z nin tercih lsitesi
C, E, D, A, B
W nin tercih listesi A, B, E, C, D
V nin tercih listesi
B, E, D, C, A
a) (A,Y), (B,V), (C,X), (E,Z) ve (D,W) evlilikleri istikrarlı( stable) mıdır? Değilse
nedenini açıklayınız.
b) İstikrarlı( Stable) evlilik algoritmasını adım adım uygulayınız.
Çözüm. a) (C,X) ve (E,Z) evlilikleri kararlı değil.
b)
A
B
1. adım
X
X
2. adım
Y
C
D
E
Y
3. adım
Z
W
Y
4. adım
X
5. adım
W
6. adım
Y
7. adım
Z
8. adım
X
9. adım
Z
10. adım
Y
11. adım
V
Soru 14 ve 15 (2011 final)
Soru 16(2011 final)