Uploaded by
gulocakismail79
Modelleme: Sistemlerin Matematiksel Modellenmesi

Modelleme
Bir sistemin matematik modeli : sistemin
dinamik davranışının matematiksel olarak
ifade edilmesidir.
Elde edilen model ile sistemin davranışı
ve uygulanacak kontrolörün performansı
önce simülasyon ortamında test edilir
sonra gerçek sistem üzerinde çalışılır.
Model Türleri
•Fiziki Modeller
– Ölçekli modeller
– Analog (deneysel) modeller
•Mathematiksel Modeller
– Analitik tabanlı
– Deney tabanlı
Model Türleri
Bir tasarım modeli genellikle analitik yöntemlerin
kullanılmasına izin verecek bir çok kabül ve
basitleştirmelere sahiptir. (Genellikle doğrusal,
zamanla değişmeyen modeller gerekir).
Doğruluğunu göstermek için bütün modelleme
ayrıntıları verilip, model denklemleri sayısal olarak
çözülür. Yani bilgisayarda.
Modelleme Süreci
1.
Modellemenin nedeni ve amacı belirtilmeli
Sistem sınırları, fonksiyonel bloklar, birbirine bağlantılı
değişkenler, girişler ve çıkışlar belirtilmeli. Fonksiyonel
bir blok diyagramı oluşturulmalı.
2. Sistem içindeki her bir elemanın modeli belirlenmeli
Mümkünse fizik kurallarını, değilse deneysel verileri
kullanarak giriş-çıkış ilişkilerini belirleyiniz.
Modelleme Süreci
3.
Her bir eleman modeli, bir bütün sistem olacak şekilde
birleştirilmeli
Denklemler birleştirilip, değişkenler sadeleştirilmeli,
çözüm için yeterli denklem olup olmadığına bakılmalı.
4. Modelin geçerliliği ve doğruluğu kontrol edilmeli.
Model denklemlerinin bir simülasyonu yapılıp, aynı
koşullarla yapılan deneysel verilerle karşılaştırılmalıdır.
Modelleme Süreci
5. Kontrol sistem tasarımına uygun bir yaklaşık model elde
edecek şekilde gerekli sadeleştirmeler yapılmalı.
– Model denklemleri doğrusallaştırılmalı
– Önemsiz dinamikler sadeleştirilerek sistem modelinin
derecesi azaltılmalı.
– Dağınık parametreli, sistemler için birleşik parametreli
yaklaşımlar kullanılmalı.
Elektriksel Eleman Modelleri
i
+
v
_
i
+
v
_
i
+
v
_
Mekanik Modeller
x
f
M
x
f
B
f
x
Mekanik Döner Hareketli Modeller
Moment/Hız
Moment/Konum
Atalet
T = J dω/dt
2 2
θ
T = J d /dt
Viscous
Sürtünme
(Amortisör)
T=Bω
T = B dθ/dt
Burulma
T = s ∫ ω dt
T=s θ
J
T, θ
T, θ
B
s
T, θ
Transformasyon Modeller
i1
i2
v1
Transformatör
v2
v1
N1
i1
N2
i2
L2
x1
L1
x2
=
v2
N2
=
N1
N1 N2
f2 , x2
Kaldıraç
f1 , x1
L2
f1
=
f2
=
L1
L2
L1
T2 , θ2
N1
T1 , θ1
Dişli
N2
T1
T2
=
N1
θ1
N2
θ2 N1
=
N2
ÖRNEK: RC Devresi
Vo(s) / Vi(s) Transfer fonksiyonunu bulunuz .
vi = R i +
1
1
=
i dt , vo
i dt
∫
∫
C
C
Laplace dönüşümü alınırsa
1
1
I ( s) , Vo ( s) =
Vi ( s ) = R +
I ( s)
sC
sC
I(s) sadeleştirilebilir.
1
Vo ( s )
1
=
Vo ( s) =
Vi ( s) or
1 + RCs
Vi ( s) 1 + τ s
Burada, τ = RC
R
vi
i
vo
Örnek: Op Amp
vi = Ri i , vo = − R f i −
Rf
1
i dt
∫
C
Ri
vi i
Laplace alınıp çözülürse;
Vi ( s ) = Ri I ( s ) , Vo ( s ) = −( R f +
Vo ( s ) = −
1
) I ( s)
sC
1
)
sC V ( s ) = − X f ( s ) V ( s ) = G ( s ) V ( s )
i
i
i
Ri
X i ( s)
(R f +
Transfer Fonksiyonu, G(s)
C
_
+
vo
Örnek: Mekanik sistem
Yay kuvveti f s = k x
dx
dt
Kütledeki net kuvvet = u − f s − f b
Kayma kuvveti f b = B v = B
x(t)
k
d 2x
dx
=
−
−
=
−
−
M 2 u f s f b u k x B , or
dt
dt
d 2x
dx
Ve çözülürse
+
M 2 B +k x =u
dt
dt
X(s) = 2 1
Laplace alınırsa;
Ms2 X(s) + BsX(s) + k X(s) =U(s)
u(t)
M
B
Ms + Bs+k
U(s)
Transfer Fonksiyonu: G(s)
Örnek : Elektrik Devresi
vi = ∑ Herbir elemanın gerilimi
di 1
= R i + L + ∫ i dt
dt C
L
R
vi
i
C
vo
Laplace alınırsa
Vi ( s ) = R I ( s ) + Ls I ( s ) +
1
I (s)
Cs
Çözülünce
s
I (s) =
Vi ( s ) = G ( s )Vi ( s )
1
+
+
Ls Rs
C
Transfer fonksiyon , G(s)
2
Mekanik ve Elektrik devresi
örneklerindeki elemanlar
arasında benzerlikler
bulunmaktadır.
• L <=> M
• R <=> B
• 1/C <=> k
Model Denklemlerinin Türleri
• Sürekli diferansiyel denklemler.
• Ayrık fark denklemleri.
• Cebirsel denklemler
Her model denklemi sınıfında alt model
sınıfları bulunur. Diferansiyel denklemlere ait
alt sınıflar aşağıdaki gibidir.
Diferansiyel Denklemler
Kısmi
Adi (Sıradan)
Doğrusal
Zamanla Değişmeyen
Doğrusal Olmayan
Zamanla Değişen
LTI - Linear Time Invariant Ordinary (Doğrusal, zamanla değişmeyen,
sıradan) diferansiyel denklemler kontrol sistemlerinin analiz ve tasarımı için
gereklidir.
Denklem
Doğrusallaştırma
y = g (x)
slope =
∂g
∂x
x = xo
y=g(x)
yo
Fonksiyonunu alalım.
Bu fonksiyonu x = xo , çalışma
noktasında Taylor Serisine açalım.
xo
∂g
y = g ( xo ) +
∂x
1 ∂2 g
( x − xo ) +
2
∂
x
2
!
x = xo
( x − xo ) 2 + Y .D.T
x = xo
Doğrusallaştırmak için, 2. ve daha yüksek dereceli
terimleri ihmal edelim
∂g
∆y =
∂x
∆x , burada ∆y = ( y − yo ) , yo = g ( xo ) , ∆x = ( x − xo )
x = xo
Sabit eğim
Çok değişkenli bir fonksiyonun doğrusallaştırılması
Eğer y = g(x1,x2, … xn ),
yo = g(x1o,x2o, … xno ). Çalışma noktasında açılırsa;
∂g
y = g ( x1o , x2 o , L xno ) +
∂x1
∂g
L +
∂xn
∂g
∆y =
∂x1
x= xo
x= xo
∂g
( x1 − x1o ) +
∂x2
( x2 − x 2 o )
x= xo
( xn − xno ) + Y .D.T .
x= xo
∂g
∆x1 +
∂x2
∆x 2
x= xo
T
[
]
=
burada, x x1 , x2 , L xn
∂g
L +
∂xn
∆x n
x= xo
Sabit eğimler
Bu, n-boyutlu
uzayda bir
hyper-düzlemi
tanımlar.
Modelleme Örneği: DA Servomotor
DA Servomotor:
Endüvi akımı, uygulanan
gerilim ve zıt emek’e
bağlıdır.
Elektromanyetik moment,
endüvi ve uyarma
akımlarının ortak etkileri ile
üretilir.
Jm
R
+
ea
--
ia
L
Tm, θm
Bm
+
eb
if
--
ef
Elektromanyetik moment ile yük momenti veya denetimsiz giriş arasındaki
fark başlangıç yükünü sürer.
DA Servomotor: Fonksiyonel Block Diyagram
ef
ea
+
--
eb
Uyarma
devresi
Endüvi
devresi
ia
ϕ
Tm Manyetik
devre
+
Ty
Mekanik
Yük
ωm
∫
θm
Zıt
e.m.k.
Bu diyagram, sistemin fonksiyonel çalışmasını ve anahtar sistem değişkenleri
aracılığıyla fonksiyonel blokların birbirine nasıl bağlandığını göstermektedir.
DA Servomotor: Model Denklemleri
Motor Momenti:
Tm = K mϕ ia ,
burada ϕ = K f i f Uyarma akısıdır.
Eğer uyarma akımı sabitse, if (t) = If böylece
Tm = K m K f I f ia = K i ia ,
burada Ki motor moment sabitidir.
Endüvi Devresi:
eb = Zıt emk = K bω m , ve ea − eb = Ra ia + La
Mekanik Yük:
d 2θ m
dθ m
= net moment = Tm − Ty − Bm
Jm
2
dt
dt
dia
dt
DA Servomotor: Model Denklemleri
(Değişkenler)
• Denklemlerde 7 değişken bulunmaktadır.
(θm , ωm , Tm , Ty , ia , ea , eb )
• 1 tane motor moment denklemi, 2 tane endüvi devresi denklemi,
1 tane mekanik yük denklemi, ve bir tane de hız denklemi
bulunmaktadır,
• 7 değişken ve 5 denklemle çözüm olabilmesi için, iki değişkenin
giriş olarak verilmesi gerekir (ea , Ty) .
DA Servomotor:Transfer Fonksiyon Modeli
Denklemlerin Laplace dönüşümleri alınıp Ea(s) ve Td(s) ye bağlı
olarak θm (s) için çözülürse;
θm (s) için çözülürse;
DA Servomotor:Transfer Fonksiyon Modeli
Setting Td(s) = 0 , the transfer function is
G(s)
Ea(s)
G(s)
θm (s)
DA Servomotor: Block Diyagram
Td(s)
Ia(s)
Ea(s)
Tm(s)+
Ki
+
+
--
Eb(s)
Kb
Not: Eğer endüvi zaman sabiti, La/Ra mekanik
zaman sabiti Jm/Bm den çok küçükse, ilk iki blok
sadeleştirilebilir.
ωm(s)
θm(s)
Servomotor Blok Diyagram İndirgemesi
Td(s)
Ea(s)
G1(s)
G2(s)
Ki
+
--
+-
G3(s)
G4(s)
+
H1(s)
Kb
Td(s)=0 , için önce iç ileri yol üzerindekiler birleştirelim.
Ea(s)
+ _
G1 G2 G3(s)
H1(s)
G4(s)
θm(s)
θm(s)
Servomotor Blok Diyagram İndirgemesi
Geri besleme çevrimini birleştirelim.
Ea(s)
G4(s)
θm(s)
Son olarak seri durumdaki blokları birleştirelim.
Ea(s)
θm(s)
Not: Elemanların son değerleri yerlerine konarak sonuç transfer
fonksiyonu sistem parametrelerine bağlı olarak elde edilebilir.
Mekanik Sistem: Durum Değişken Modellemesi
Yay kuvveti f s = k x
dx
dt
Kütledeki net kuvvet = u − f s − f b
Kayma kuvveti f b = B v = B
x(t)
k
Ms2 X(s) + BsX(s) + k X(s) =U(s)
M
B
d 2x
dx
=
−
−
=
−
−
M 2 u f s f b u k x B , or
dt
dt
d 2x
dx
Ve çözülürse
+
M 2 B +k x =u
dt
dt
X(s) = 2 1
Laplace alınırsa;
u(t)
Ms + Bs+k
U(s)
Transfer Fonksiyonu: G(s)
Mekanik Sistem: Durum Değişken Modellemesi
d 2x
dx
M 2 +B +k x =u
dt
dt
2. Dereceden bir denklem, 2 tane
1. Derce denklem olarak
yazılabilir.
Mekanik Sistem: Durum Değişken Modellemesi
A: Sistem matrisi
B: Giriş matrisi
C: Çıkış matrisi
Durum
vektörü
Çıkış
vektörü
Durum
değişkenleri
END OF THIS CHAPTER
Simülasyon Diyagramları
Dif. Denklemlerden,
Durum denklemlerinden,
Transfer fonksiyonlarından
Elde edilebilirler.
Blok diyagramları veya işaret akış grafikleri ile temsil edilirler.
Simülasyon diyagramının en basit elemanı INTEGRATÖR dür.
Başlangıç koşulları
ihmal ediliyor.
Bu denklemler, blok diyagramları veya işaret akış grafikleri ile aşağıdaki
gibi temsil edilirler.
Simülasyon Diyagramları
y(t)
X(s)
X(s)
Y(s)
s-1
X(s)
Y(s)
Y(s)
Simülasyon Diyagramları
ÖRNEK
2
d x
dx
+
M 2 B +k x =u
dt
dt
+
Transfer Fonksiyonundan Simülasyon Diyagramına
U(s)
U(s)
Y(s)
Z(s)
Y(s)
Transfer Fonksiyonundan Simülasyon Diyagramına
ÖRNEK
(Başlangıç koşulları sıfır)
Transfer Fonksiyonundan Simülasyon Diyagramına
ÖRNEK
Durum
denklemleri
Çıkış
denklemi
Transfer Fonksiyonundan Simülasyon Diyagramına
ÖRNEK
+ +
+
+
Kontrol
Kanonik
Biçim
Simülasyon Diyagramından durum denklemine
ÖRNEK
Şekilden;
++
+
+
Transfer Fonksiyonundan Simülasyon Diyagramına
olsun
İle çarpalım
Bu yapıdaki bir transfer fonksiyonunun genel kazanç bağıntısı (Mason kazanç
bağıntısı) kullanılarak elde edilebileceği dikkate alınıp, genel kazanç bağıntısı
hatırlanırsa;
Transfer Fonksiyonundan Simülasyon Diyagramına
Girişi çıkışa aktaran ileri yol kazançları
∆ nın işaret akış diyagramlarında i inci ileri yolu ile temas etmeyen kısmı
1 - (tüm bireysel çevrim kazançlarının toplamı
+ (temas etmeyen çevrimlerin ikili gruplar halinde çarpımlarının toplamı)
- (temas etmeyen çevrimlerin üçlü gruplar halinde çarpımlarının toplamı)
+ ................
Transfer Fonksiyonundan Simülasyon Diyagramına
Buradaki denklemlerden,
Olduğu görülmektedir. Bu, girişten çıkışa 3 tane yol var demektir.
u
y
Transfer Fonksiyonundan Simülasyon Diyagramına
y
u
+
+
+
+
+
+
+
Transfer Fonksiyonundan Simülasyon Diyagramına
Paydayı temsil eden denklemlerden,
0
y
Transfer Fonksiyonundan Simülasyon Diyagramına
y
+
+
-
-
-
Transfer Fonksiyonundan Simülasyon Diyagramına
+
+
+
+
+
+
+
+
-
-
Paydadan elde
edilen diyagram
+
-
Paydan elde
edilen diyagram
Bu iki simülasyon diyagramı birleştirilerek genel simülasyon diyagramı elde edilir.
Transfer Fonksiyonundan Simülasyon Diyagramına
x3 +
+
x1
x2 +
-
-
Gözlemci
kanonik
biçim
+
-
+
Simülasyon Diyagramından durum denklemine
Gözlemci
kanonik
biçim
Durum
denk.
+
x3 +
-
+
+
x2 +
-
Şekilden:
x1
Transfer Fonksiyonundan Durum denklemine
Kontrol
kanonik
biçim
İki farkli simülasyon diyagramı
N-adet simülasyon
diyagramı elde edilebilir.
İki farkli
durum
denklemi
Gözlemci
kanonik
biçim
Transfer Fonksiyonundan Durum denklemine
Transfer fonksiyonuna sahip bir sistem için en az üç
tane farklı durum değişken modeli elde edininiz.
Aşağıda bir DA motoru hız denetimine ait açık çevrim blok
diyagramı verilmektedir. Bu sistemin durum denklemlerini elde
ediniz.
Uyarma
Uyarma
gerilimi
akımı
Hız
R(s)
U(s)
Denetleyici
I(s)
Y(s)
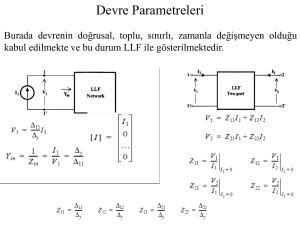
Durum denkleminden Transfer Fonksiyonuna
U(s)
SISO bir sistemin durum
değişkenlerini alalım.
alınırsa
Y(s)
Durum denkleminden Transfer Fonksiyonuna
A, B, C ve D matris ve vektörleri aşağıdaki gibi verilen sistemin
kutuplarını, sıfırlarını, karakteristik denklemişni ve transfer
fonksiyonunu bulunuz.
Durum denkleminden Transfer Fonksiyonuna
Sıfırlar: -(-2+j1.7321)
-(-2-j1.7321)
Kutuplar:
-1 ve -2
Durum denkleminden Transfer Fonksiyonuna
Matlab komut penceresi
Durum_tf.m dosyası
% durum denkleminden
% transfer fonksiyonuna
A=[0 1;-2 -3];
B=[1;2];
C=[1 0];
D=1;
[pay, payda]=ss2tf(A,B,C,D)
sifirlar=roots(pay)
Kutuplar=roots(payda)
pay =
1
4
7
payda =
1
3
2
sifirlar =
-2.0000 + 1.7321i
-2.0000 - 1.7321i
Kutuplar =
-2
-1
Aşağıdaki konuları gözden geçirip, verilen problemi çözünüz.
Durum denklemlerinin Laplace dönüşümü ile çözümü
Durum geçiş matrisinin ters Laplace dönüşümü ile çözümü
Denkleminin genel çözüm biçimlerini araştırınız.
Durum geçiş matrisinin sonsuz serilerle çözümü
A, B, C ve D matris ve vektörleri aşağıdaki gibi verilen sistemin durum
denklemlerini yukarda sıralanan yöntemlerle çözerek x(t) değerlerini
bulunuz
Bir sistemin durum denklemleri o sistemin diferansiyel denklemlerinden veya
transfer fonksiyonundan elde edilebilir. Durum denklemlerinin çözümü için
farklı yöntemler uygulanmaktadır.
Laplace
Aynı işlemler 2. Denklem seti için de yapılırsa;
Bütün denklemlerin Laplace dönüşümleri benzer şekilde alınıp bir araya
getirilirse aşağıdaki genel yapı elde edilir.
Bu denklem X(s) için düzenlenirse;
Bu denklemin ters Laplace dönüşümü alınarak x(t) durum vektörü elde edilir.
DURUM GEÇİŞ MATRİSİ
(temel matris olarak da isimlendirilir.)
NOTLAR:
Derecesi n olan bir sistemin durum geçiş matrisinin derecesi de n dir.
Bir matrisin ters Laplace dönüşümü, o matrisin elemanlarının ters Laplace
dönüşümleri olarak tanımlanır.
Verilen son denklemin ters Laplace dönüşümünü bulmak oldukça zor, zaman
alıcı, ve hata yapma olasılığı fazladır.
Durum vektörü x(t) nin hesaplanması için en pratik yol bilgisayar
simülasyonudur.
Transfer fonksiyonuna sahip sistemin durum denklemlerini gözlemci kanonik
biçimde yazarak çözünüz.
Devam...
Durum geçiş matrisi:
Devam...
Genel çözüm denkleminin ikinci kısmını u(t)=1 basamak giriş için çözünüz.
Devam...
Böylece
Denkleminin çözümü:
s-domeninde iki terimin
çarpımından oluşan bu
terimin ters Laplace
dönüşümü bir Konvolüsyon
integrali olarak ifade
edilebilir.
Konvülasyon teoremine göre bu çözüm aşağıdaki gibi yazılabilir:
Durum geçiş
matrisi, durum
denklemlerinin
çözümünde bir
merkez teşkil
etmektedir.
Başlangıç koşullarını
içeren sıfır giriş kısmı
Giriş işaretine bağlı sıfır durum
(zorlanmış kısım)
Bir önceki örnekte elde edilen durum geçiş matrisini ve B giriş
vektörünü basamak giriş işareti ile birlikte kullanarak x(t)
bağıntısının sağ tarafında verilen konvolüsyon integralini
hesaplayınız.
Devam...
Elde edilen bu zorlanmış çözüm daha önce elde edilen çözümle aynıdır. Toplam
çözümü elde etmek için durum geçiş matrisinin sıfır giriş kısmındaki Φ(t)x(0)
çözümünün de buna eklenmesi gerekir.
Şu ana kadar yapılan çözümler ya Laplace dönüşümü, ya da Laplace dönüşümü
ile konvolüsyon integralinin birleştirilmesiyle elde edildi. Bu yöntemlerin her ikisi
de uzun ve hata yapmaya açıktır.
Bütün sistem girişlerinin sıfır olduğu durum için durum denklemleri:
U(t)=0
Böylece;
Denkleminde U(s)=0 yani u(τ)=0 için
Denkleminin çözümü bir vektör olarak elde edilir. Öyle ki vektör
aşağıdaki gibi bir seriyle ifade edilebilir.
Ai : Bilinmeyen katsayılar
t : zaman ölçeği
Bu denklemin türevi alınırsa;
Şimdi aşağıdaki işlemleri gerçekleştirelim:
Yukardaki son denklemi t=0 için elde edelim
Bu son denklemin türevini alıp, sonucu t=0 için yazalım
Tekrar türevini alıp, t=0 için yeniden yazalım
Bu işlemin her tekrarlanmasında bilinmeyen Ai matrisinde bir
denklem elde edilir.
Bu işlemin etkisiyle yukarıdaki son denklemde ti katsayıları
eşitlenmektedir.
Bu işlemler yapılırsa:
t=0
Türev alıp, t=0 için düzenlenirse
Tekrar türev alıp, t=0 için düzenlenirse
T=0 için aşağıdaki denklem yeniden yazılırsa;
Olduğu görülür. Ve diğer matrisler
bağıntısından elde edilir.
Olarak elde edilince,
Olarak
belirlenir.
Böylece durum geçiş matrisi aşağıdaki gibi
yazılabilir.
Bu ifade Taylor serisine benzemekte olup, skaler bir exponansiyel olarak ifade
edilebilir.
Kullanılan notasyona uygun olması bakımından durum geçiş matrisi için;
Yazılabilir.
Serisinin sonlu bir sayıda sıfır olmayan terimlere sahip olduğu durum için transfer
fonksiyonu
Olan bir sistemi ele alalım.
Verilen sistem aşağıdaki işaret akış grafiği ile temsil edilebilir.
U(s)
Böylece durum denklemleri:
Y(s)
U(s)
Y(s)
Devam...
Şekilden:
Benzer şekilde;
Devam...
Böylece
denkleminden
Durum geçiş matrisi;
Bu örnekte durum geçiş matrisi kolayca elde edildi. Ancak her zaman
böyle kolay olmayabilir.
İkinci dereceden bir sistem aşağıdaki matrislerle temsil
edilmektedir.
Aşağıdaki koşullar için çözümleri bulunuz.
Önce durum geçiş matrisi hesaplanmalı.
Devam...
Aşağıdaki sistem için Φ(t) durum geçiş matrisini hesaplayınız.
Olduğuna göre
Devam...
% MATLAB Program› kontrol1.m
% transfer fonksiyonundan
% durum degiskenlerine donusum
% pay ve payda verileri
num=[2 8 6];
den=[1 8 16 6];
[A,B,C,D]=tf2ss(num,den);
printsys(A,B,C,D)
» kontrol1
a=
x1
x2
x3
x1
x2
x3
-8.00000 -16.00000 -6.00000
1.00000
0
0
0
1.00000
0
b=
x1
x2
x3
u1
1.00000
0
0
y1
x1
2.00000
y1
u1
0
c=
d=
x2
x3
8.00000
6.00000
% kontrol2.m
% Durum matrisi ve
% diger veriler
A=[0 -2; 1 -3]; B=[2;0];
C=[1 0];
D=[0];
dt=0.2;
DGM=expm(A*dt);
DGM
» kontrol2
DGM =
0.9671
0.1484
-0.2968
0.5219
lsim fonksiyonu
% program kontrol3.m
% lsim fonksiyonu ile durumlarin
% ve cikisin elde edilmesi
% Durum matrisi ve diger veriler
A=[0 -2; 1 -3]; B=[2;0]; C=[1 0];
D=[0];
x0=[1 1];
t=[0:0.01:1];
u=0*t;
[y,x]=lsim(A,B,C,D,u,t,x0);
subplot(211), plot(t,x(:,1))
xlabel('time[sec]'), ylabel('x1')
subplot(212), plot(t,x(:,2))
xlabel('time[sec]'), ylabel('x2')
ÖRNEK
Aralarında yay bulunan iki kütleli bir sistemin
simülasyonu (ref. Modern Control Systems by Dorf
and Bishop page 160)
% program Ornek01.m
% Ornek simulasyon programi .Aralarinda yay bulunan iki kutleli bir sistem
% Model parametreleri
k=10; M1=0.02;
M2=0.0005; b1=410e-03; b2=4.1e-03;
t=[0:0.001:1.5];
% durum degisken modeli verileri
A=[0 0 1 0; 0 0 0 1; -k/M1 k/M1 -b1/M1 0; k/M2 -k/M2 0 -b2/M2 ];
B=[0; 0; 1/M1; 0]; C=[0 0 0 1]; D=0;
u=1; % Birim basamak simulasyonu
y=step(A,B,C,D,u,t);
plot(t,y)
birimler
xlabel('time[sec]'), ylabel('hareket hizi (m/s)')
k : kg/m
grid
b : kg/m/s
m : kg
ÖRNEK
Aralarında yay bulunan iki kütleli bir sistemin
simülasyonu (ref. Modern Control Systems by Dorf
and Bishop page 160)
ÖRNEK
Sürekli Miknatisli Dogru Akim motorunun
Simulasyonu - 01
% Program Kontrl04.m
% PMDC motor denklemleri
% veriler
Va=36;
Ia=15; Inl=1.62;
Ra=1.4;
La=0.00805;
Ka=0.095;
Km=Ka;
Nn=3400;
Bm=4.31e-4;
Jm=7.432e-4;
K0=0.106309;
K1=8.4e-5;
K2=1.1e-6;
A=[ -(Ra/La)
-(Ka/La)
Km/Jm -(Bm/Jm) ];
B=[ 1/La
0
0
-(1/Jm) ];
» kontrl04
»A
A=
-173.9130 -11.8012
127.8256 -0.5799
»B
B=
1.0e+003 *
0.1242
0
0
-1.3455
Sürekli Miknatisli Dogru Akim motorunun
Simulasyonu - 02
% PMDC motor denetimsiz tepkesi
% veriler
Va=36;
Ia=15;
Inl=1.62;
Nn=3400;
Ra=1.4;
La=0.00805;
Ka=0.095;
Km=Ka;
Bm=4.31e-4;
Jm=7.432e-4;
K0=0.106309; K1=8.4e-5;
K2=1.1e-6;
A=[ -(Ra/La)
-(Ka/La)
Km/Jm
-(Bm/Jm) ];
B=[ 1/La; 0]; C=[0 1]; D=[0 ] ;
TL=0;
% Birim basamak simulasyonu
u=1; t=[0:0.01:2];
y=step(A,B,C,D,u,t);
plot(t,y,'r')
xlabel('ZAMAN (s)');
ylabel('Motor Hizi (rad/s)')
ÖRNEK
ÖRNEK
Sürekli Miknatisli Dogru Akim motorunun
Simulasyonu - 02
Jm=7. 432×10-4
ÖRNEK
Sürekli Miknatisli Dogru Akim motorunun
Simulasyonu - 02
Jm=7. 432×10-6
ÖRNEK
Sürekli Miknatisli Dogru Akim motorunun
Simulasyonu - 02
Jm=7. 432×10-3
SÜREKLI MIKNATISLI DA MOTORUNUN
ZAMAN TEPKELERI
% Program Kontrl04.m
% PMDC motor denetimsiz tepkesi. Transfer Fonksiyonu (TL=0 icin)
% Birim basamak tepkesi, Birim darbe tepkesi, birim rampa tepkesi
% veriler
Va=36;
Ia=15;
Inl=1.62;
Nn=3400;
Ra=1.0;
La=0.08;
Ka=0.095;
Km=Ka; %
La=0.00805;
Bm=4.31e-4;
Jm=7.432e-4;
% Jm=7.432e-6; % Jm=7.432e-3;
K0=0.106309; K1=8.4e-5;
K2=1.1e-6;
A=[ -(Ra/La)
-(Ka/La)
Km/Jm
-(Bm/Jm) ];
B=[ 1/La; 0 ];
C=[0 1];
D=[0 ] ; TL=0;
SÜREKLI MIKNATISLI DA MOTORUNUN
ZAMAN TEPKELERI
[num, den]=ss2tf(A,B,C,D); % Transfer fonksiyonu
% Bulunan transfer fonkiyonu:
% num = 1597.8;
den = S^2 +13.0799 S + 159.0420
% Birim basamak tepkesi
u=1; t=[0:0.01:1];
[ys1,xs1,ts1]=step(A,B,C,D,u,t);
[ys2,xs2,ts2]=step(num,den,t);
% Birim darbe tepkesi
[yi1,xi1,ti1]=impulse(A,B,C,D);
[yi2,xi2,ti2]=impulse(num,den,t);
% Birim rampa tepkesi
num2=[0 num];
den2=[den 0];
[yr1,xr1,tr1]=step(num2,den2,t);
AA=[A zeros(2,1);C 0]; BB=[B;0];
CC=[0 0 1]; DD=0; % y=x3=z alinirsa
[yr2,xr2,tr2]=step(AA,BB,CC,DD);
SÜREKLI MIKNATISLI DA MOTORUNUN
ZAMAN TEPKELERI
% Grafikler
subplot(211)
plot(ts1,ys1)
xlabel('ZAMAN (s)'); title('Birim Basamak Tepkesi (rad/s)'); grid
subplot(212)
plot(ts2,ys2); xlabel('ZAMAN (s)'); title('Birim Basamak Tepkesi (rad/s)'); grid;pause
subplot(211)
plot(ti1,yi1); xlabel('ZAMAN (s)'); title('Birim Darbe Tepkesi (rad/s)'); grid
subplot(212)
plot(ti2,yi2); xlabel('ZAMAN (s)'); title('Birim Darbe Tepkesi (rad/s)'); grid;pause
subplot(211)
plot(tr1,yr1,'o',t,t,'-'); xlabel('ZAMAN (s)'); title('Birim Rampa Tepkesi (rad/s)');grid
subplot(212)
plot(tr2,yr2,'o',t,t,'-'); xlabel('ZAMAN (s)'); title('Birim Rampa Tepkesi (rad/s)'); grid
SÜREKLI MIKNATISLI DA MOTORUNUN
ZAMAN TEPKELERI
SÜREKLI MIKNATISLI DA MOTORUNUN
ZAMAN TEPKELERI
SÜREKLI MIKNATISLI DA MOTORUNUN
ZAMAN TEPKELERI