Kapılardaki gecikme

Kapılardaki gecikme
•
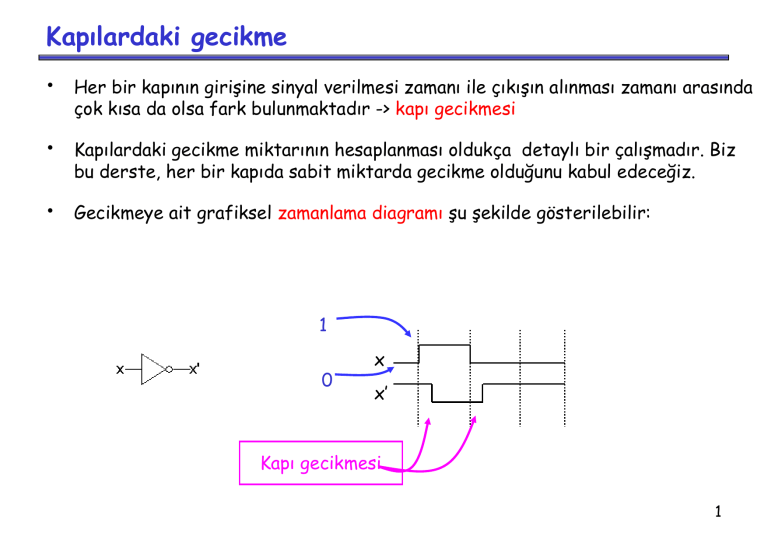
Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında
çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi
•
Kapılardaki gecikme miktarının hesaplanması oldukça detaylı bir çalışmadır. Biz
bu derste, her bir kapıda sabit miktarda gecikme olduğunu kabul edeceğiz.
•
Gecikmeye ait grafiksel zamanlama diagramı şu şekilde gösterilebilir:
1
0
x
x’
Kapı gecikmesi
1
Elde eklemede gecikmeler: (Dalgalı Elde Toplayıcı)
1
9
8
7
6
5
4
3
2
2
•
•
•
4-bitlik toplama devresine ait diyagram incelenirse:
Buna dalgalı elde toplayıcı ismi verilebilir. Çünkü A0, B0 ve EG girişleri sola
doğru dalgalanmaktadır; ta ki EÇ ve T3 hesaplanabilinceye kadar!
Dalgalı elde toplayıcı yavaştır!
– A0, B0 ve EG değerlerinin sisteme verilmesinden EÇ ve T3’ün
hesaplanmasına kadar geçen yol oldukça uzundur.
– n-bitlik bir dalgalı elde toplayıcıda en uzun yol: 2n+1 kapıdır.
– Bu örnekteki 4-bitlik toplama için en uzun yol 9 kapıdır.
– Örneğin 64-bitlik toplayıcıda, en uzun yol 129 kapıdır!
1
9
8
7
6
5
4
3
2
3
Eldeyi hesaplamak için daha hızlı bir yöntem:
•
•
Çıkıştaki eldeyi hesaplayabilmek için önceki bütün
aşamalardaki eldelerin hesaplanmasını beklemek
yerine, 2-seviyeli bir devre ile doğrudan
hesaplayabiliriz. Böylece ana devredeki gecikmeyi
azaltmış oluruz.
Öncelikle iki fonksiyon tanımlayalım:
– “üreteç” (generate) fonksiyonu gi , i inci
aşamada elde çıkışı olduğunda 1 olsun.
(Yani, Ai ve Bi 1 olduğunda).
–
•
gi = AiBi
“yayılım” (propagate) fonksiyonu pi , gelen bir
elde olduğunda (Eg=1) 1 olsun.
(Yani, Ai=1 veya Bi=1, ama ikisi birden değil).
pi = Ai ⊕ Bi
Bu durumda elde çıkış fonksiyonunu yeniden
yazabiliriz:
ei+1 = gi + piei
pi
gi
Ai
Bi
Ei
Ei+1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
1
0
1
1
1
4
Cebirsel olarak elde ifadesi
•
i inci aşama için hesapladığımız ei+1 = gi + piei fonksiyonu yardımıyla bazı elde
çıkışları yazılırsa:
e1 = g0 + p0e0
e2 = g1 + p1e1
= g1 + p1(g0 + p0e0)
= g1 + p1g0 + p1p0e0
e3 = g2 + p2e2
= g2 + p2(g1 + p1g0 + p1p0e0)
= g2 + p2g1 + p2p1g0 + p2p1p0e0
e4 = g3 + p3e3
= g3 + p3(g2 + p2g1 + p2p1g0 + p2p1p0e0)
= g3 + p3g2 + p3p2g1 + p3p2p1g0 + p3p2p1p0e0
•
Bu ifadelerin hepsi çarpımlar toplamı olduğundan, sadece 2-seviyeli gecikme
olacaktır.
5
4-bitlik İleri bakmalı elde devresi (Look Ahead Carry)
6
•
Bu bir ileri bakmalı elde devresi dir.
•
Ne kadar hızlı?
–
–
–
Tasarlamış olduğumuz 4-bit toplayıcı için belki çok fazla değil:
9 kapıdan 4 kapıya indi.
Ancak bir 16-bitlik toplayıcı için: 33 -> 8
Günümüzdeki yeni mikroişlemcilerde kullanılan 64-bitlik toplayıcılar için: 129
-> 12 !
•
Normal elde toplayıcıdaki gecikme toplayıcının boyutu ile doğrusal olarak
artarken, ileri bakmalı elde toplayıcıda logaritmik olarak artmaktadır.
•
Karmaşıklık ve performans açısından bir Trade-off söz konusudur: Normal elde
toplayıcı basit ancak yavaştır. Öte yandan, ileri bakmalı elde toplayıcı ise hızlı
ancak daha karmaşıktır.
7
İşaretli Sayılar
•
Şu ana kadar kullandığımız binary sayıların tamamı işaretsiz (pozitif) sayılardır.
•
“Negatif sayılar” ve ardından da “Çıkarma İşlemi” ?
•
İşaretli sayılar‘ın gösterimi için 3 farklı yöntem inceleyeceğiz.
•
Çıkarma işlemi: x - y
i. Her iki sayıyı da işaretli sayıya dönüştürmek
ii. İşaretli bir sayının negatifini almak: y -> -y
iii. İki işaretli sayıyı toplamak: x + (-y)
•
•
Not-1: Bir işaretli sayı için “Negatifini alma” kavramı: x -> -x
Not-2: Değişkenler için “Toplama işlemi”: x+y (VEYA işlemi ile karıştırılmamalı!)
8
1) İşaretli Büyüklük Gösterimi
•
Normal matematikte bir büyüklüğün pozitif veya negatif olduğunu belirtmek için
sayının önüne + veya – işareti eklenir.
•
Binary sayılarda da sayının önüne bir bitlik ekstra bir işaret biti eklenebilir:
–
–
•
0 işaret biti sayının pozitif
1 işaret biti ise sayının negatif olduğunu gösterir.
Örnekler:
11012 = 1310
0 1101 = +1310
1 1101 = -1310
(4-bitlik bir işaretsiz sayı)
(5-bitlik bir işaretli pozitif sayı)
(5-bitlik bir işaretli negatif sayı)
01002 = 410
0 0100 = +410
1 0100 = -410
(4-bitlik bir işaretsiz sayı)
(5-bitlik bir işaretli pozitif sayı)
(5-bitlik bir işaretli negatif sayı)
9
İşaretli Büyüklükte Toplama
•
Bir sayının negatifini almak için doğrudan işaret bitini tersine çevirmek yeterlidir.
•
Bu yöntemde sayıları toplamak ise zordur. Ortaokulda öğretilen toplama yöntemi
geçerlidir:
–
–
•
Eğer sayılar aynı işaretli ise, büyüklükleri topla ve işaret aynı kalsın.
Eğer sayıların işaretleri farklı ise, büyüklükler içinden büyük olanından küçüğü
çıkar ve büyük olan büyüklüğün işaretini sonucun işareti olarak al.
Bu çıkarma yöntemi oldukça karmaşık yapıda bir devre ile gerçekleştirilebilir.
+ 3
+ -6
-2
7
4
6
9
7
8
çünkü:
-
5
6
3
2
13
4
7
6
17
7
9
8
10
2) 1’e Tümleme Gösterimi
•
•
•
Bir başka yaklaşım olan 1’e tümleme yönteminde, sayının negatifinin alınması
sayıdaki her bir bitin tümleyeninin alınması ile gerçekleştirilir: 1 -> 0 ve 0 -> 1
Pozitif için 0, negatif için 1 olan işaret bitinin de diğerleri ile birlikte tümleyeni
alınır.
Örnekler:
11012 = 1310
0 1101 = +1310
1 0010 = -1310
(4 bitlik bir işaretsiz sayı)
(5 bitlik bir pozitif 1’e tümleme sayısı)
(5 bitlik bir negatif 1’e tümleme sayısı)
01002 = 410
0 0100 = +410
1 1011 = -410
(4 bitlik bir işaretsiz sayı)
(5 bitlik bir pozitif 1’e tümleme sayısı)
(5 bitlik bir negatif 1’e tümleme sayısı)
11
1’e Tümlemede Toplama
•
1’e tümlemede sayıların toplamı:
–
–
•
Öncelikle sayılar işaretsizmiş gibi toplanır. (İşaret bitleri de dahil olarak)
Ardından Elde çıkışı alınarak toplama eklenir.
Örneğin:
0111
+
1011
1 0010
0010
+
1
0011
•
(+7)
+ (-4)
(+3)
0011
+
0010
0 0101
0101
+
0
0101
(+3)
+ (+2)
(+5)
İşaretli büyüklükte toplamaya göre bu daha basit bir yöntemdir.
12
3) 2’ye Tümleme Gösterimi
•
Son yaklaşım ise 2’ye tümleme. Sayının negatifini almak için öncelikle her bitin
tümleyeni alınır (1’e tümlemede olduğu gibi); Ardından, elde edilen sayıya 1 eklenir.
•
Örnekler:
11012
0 1101
1 0010
1 0011
= 1310
= +1310
= -1310
= -1310
01002 = 410
0 0100 = +410
1 1011 = -410
1 1100 = -410
(4-bitlik bir işaretsiz sayı)
(5 bitlik bir pozitif 2’e tümleme sayısı)
(5 bitlik bir negatif 1’e tümleme sayısı)
(5 bitlik bir negatif 2’e tümleme sayısı)
(4-bitlik bir işaretsiz bir sayı)
(5 bitlik bir pozitif 2’e tümleme sayısı)
(5 bitlik bir negatif 1’e tümleme sayısı)
(5 bitlik bir negatif 2’e tümleme sayısı)
13
2’ye Tümlemede Toplama
•
2’ye tümleme alma diğerlerine göre biraz daha fazla iş gerektiriyor ancak buna
karşılık, toplama işlemi diğer iki yönteme göre daha kolay.
•
A + B için:
–
–
A ve B’yi işaretsiz sayı toplamı yap (işaret bitleri de dahil)
Elde çıkışını önemseme, at.
• Örnek: 0111 + 1100 için (yani (+7) + (-4)):
–
–
Öncelikle 0111 + 1100 toplamını işaretsiz sayılarmış
gibi yap:
Elde çıkışını (1) at. Sonuç: 0011 (+3).
• Örnek: iki negatif sayının toplamı: 1101 + 1110 ((-3) + (-2))
– Elde çıkışı (1)’i at. Sonuç: 1011 (-5).
01 1 1
+ 1 1 00
1 001 1
1 1 01
+ 1110
1 1 01 1
14
İşaretli sayı sistemlerinin karşılaştırılması
• Pozitif sayılarda her üç gösterim
de aynı.
•
İşaretli büyüklükte ve 1’e
tümlemede 0 a karşılık gelen iki
gösterim var. Bu karmaşıklığa
sebep olabilir.
•
2’ye tümlemede ise asimetrik bir
aralık söz konusudur. Negatif
sayılarda pozitiflere göre 1 tane
fazla sayı var. -8 var ama +8 yok.
•
Buna rağmen, 2’ye tümleme tercih
edilir. Çünkü tek bir 0 var ve
toplama algoritması en basiti.
Decimal
İ.B.
1’e tüm.
2’ye tüm.
7
6
5
4
3
2
1
0
-0
-1
-2
-3
-4
-5
-6
-7
-8
0111
0110
0101
0100
0011
0010
0001
0000
1000
1001
1010
1011
1100
1101
1110
1111
—
0111
0110
0101
0100
0011
0010
0001
0000
1111
1110
1101
1100
1011
1010
1001
1000
—
0111
0110
0101
0100
0011
0010
0001
0000
—
1111
1110
1101
1100
1011
1010
1001
1000
15
İşaretli sayı sistemlerinin aralıkları
•
3 yöntemden her birinde pozitif ve negatif kaç tane sayının gösteriminin söz
konusu olduğuna bakılırsa:
En küçük
En büyük
•
İşaretsiz
İşaretli
Büyüklük
1’e
Tümleme
2’ye
Tümleme
0000 (0)
1111 (15)
1111 (-7)
0111 (+7)
1000 (-7)
0111 (+7)
1000 (-8)
0111 (+7)
Genel olarak, n-bitlik sayı (işaret biti dahil) için, aralıklar:
En küçük
En büyük
İşaretsiz
İşaretli
Büyüklük
1’e
Tümleme
2’ye
Tümleme
0
2n-1
-(2n-1-1)
+(2n-1-1)
-(2n-1-1)
+(2n-1-1)
-2n-1
+(2n-1-1)
16
İşaretli sayıları decimale çevirme - Örnek:
•
110101 sayısını decimale çevirelim:
İşaret biti 1 olduğundan, bu bir negatif sayıdır. En kolay yöntem öncelikle
bulunduğu formatta pozitif haline çevirmektir.
(a) eğer sayı işaretli büyüklük formatında ise,
Orjinal sayının (110101) negatifi alınırsa: 010101. Bu sayı decimal olarak +21 dir.
Öyleyse, 110101 sayısı -21 e karşılık gelir.
(b) eğer sayı 1’e tümleme formatında ise,
110101 sayısını 1’e tümlemede negatifi alınırsa: 001010 = +1010. Öyleyse,
orjinal sayı -1010.
(c) eğer sayı 2’ye tümleme formatında ise
110101 sayısını 1’e tümlemede negatifi alınırsa: 001011 = 1110. Öyleyse, orjinal
sayı = -1110.
! Binary işaretli sayılar gösterildikleri sisteme bağlı olarak farklı bir sayıya karşılık
gelirler.
17
Çıkarma Devresi Tasarımı
•
Bir çıkarma devresini işaretsiz sayı toplama devresinde olduğu gibi doğrudan
tasarlayabiliriz.
•
Ancak, eğer 2’ye tümleyen yöntemi kullanılırsa çıkarma problemi toplama
problemine dönüşmektedir. Cebirsel olarak,
A - B = A + (-B)
•
Böylece A’dan B’yi çıkarmak yerine A’ya B’nin 2’ye tümleyenini eklenebilir.
•
Böylece işaretsiz toplama devresi donanımını tekrar kullanabiliriz.
18
2’ye tümleme çıkarma devresi
•
•
•
•
A – B’yi bulmak için:
–
–
B nin her bir bitinin tümleyeni alınır
Eg Elde girişi 1 olarak set edilir.
Sonuç: A + B’ + 1 (B’ + 1: B’nin 2’ye tümleyenidir.)
Not: A3, B3 ve S3 işaret bitleridir.
Toplama ve çıkarma devreleri arasındaki tek fark:
– Çıkarılan sayının (B3 B2 B1 B0) tümleyeni alınmalı
– İlk elde girişi 0 yerine 1 olarak set edilmeli
19
“Toplama ve Çıkarma” Devresi
•
•
Toplama ve çıkarmayı tek bir devrede tasarlamak çok da zor değildir!
XOR kapısı B girdisinin tümleyenini alma şansı verir:
X⊕0=X
X ⊕ 1 = X’
•
Ç = 0 ise, XOR kapılarının çıkışları B3 B2 B1 B0 ve elde girişi 0.
Devrenin çıkışı: A + B + 0 (=A + B).
•
Ç = 1 ise, XOR kapılarının çıkışları B3’ B2’ B1’ B0’ ve elde girişi 1.
Böylece, devrenin çıkışı: 2’ye tümleyen çıkarmadır: A - B
20