MATLAB ile Sembolik Analiz

MATLAB ile Sembolik
Analiz
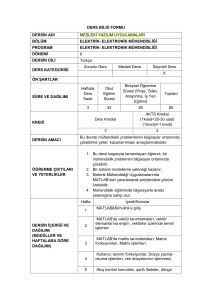
MATRİSLER VE MATRİSLERLE İŞLEMLER
DİZİLER – Bir Boyutlu Dizi (Vektör)
 Liste şeklinde dizi oluşturma
Değişken_adı = [ Vektör Elemanları]
Satır Vektör: x = [ 1 5 7 -3 6 4 5 8 ] veya x = [ 1, 5, 7, -3, 6, 4, 5, 8 ]
Sütun Vektör: x = [ 1; 5; 7; -3; 6; 4; 5; 8 ] veya x=[2
3
5]
DİZİLER – Bir Boyutlu Dizi (Vektör)
• Belli bir kurala göre sıralı giden diziler
•
İlk eleman, artım miktarı, son eleman ile belirlenen diziler
Değişken_adı = [ m:q:n] veya Değişken_adı = m:q:n
m=dizinin ilk elemanı, q=artım miktarı, n=dizinin son elemanı
•
İlk eleman, son eleman ve terim sayısı ile belirlene diziler
Değişken_adı = linspace(xi, xf, n)
xi=ilk eleman, xf=son eleman, n=eleman sayısı (Bu değer girilmezse, varsayılan olarak 100 kabul edilir.)
MATRİSLER
• Matris Oluşturma
Değişken_adı=[ilk satır elemanları; ikinci satır elemanları; … ; son satır elemanları]
VEYA
Örnek
A matrisini oluşturan komutu yazınız.
Zeros, Ones ve Eye
Sıfır Matrisi
‘ : Transpoze İşleci
Bir Matrisi
Birim Matris
Dizi Adresleme
• V bir vektör ise V(n) ile vektörün n inci elemanına erişilir.
• A bir matris ise A(m,n) ile matrisin m inci satır n inci sütun elemanına erişilir.
Dizi Adresleme – Kolon Operatörü (:)
• Vektörler
•
•
V(:) – Vektörün tüm elemanlarını ifade eder. (Yani, V ile aynıdır)
V(m:n) – Vektörün m ile n arasındaki elemanlarını ifade eder.
Dizi Adresleme – Kolon Operatörü (:)
• Matrisler
•
•
•
•
•
A(:,n) – Matrisin n inci sütunundaki tüm elemanlar
A(m,:) – Matrisin n inci satırındaki tüm elemanlar
A(:,m:n) – Matrisin m ve n arasındaki (m ve n dahil) tüm sütun elemanları
A(m:n,:) – Matrisin m ve n arasındaki (m ve n dahil) tüm satır elemanları
A(m:n, p:q) – Matrisin m ve n satırları ile p ve q sütunları arasındaki tüm elemanlar
Dizi Adresleme – Kolon Operatörü (:)
Dizi Adresleme – Daha Fazlası
v vektörünün 3 üncü, 5 inci ve 7-10
arası elemanlarını nasıl alırız?
A matrisinin 1 inci, 3 üncü satırı, 1 inci 3 üncü
sütunu ve 5 ile7 inci sütun arası elemanlarını nasıl
alırız?
Var olan değişkenlere elemanlar ekleme
• Bir Vektöre Elemanlar Ekleme
DF vektörünün sonuna 10 15 20 25 30 35 elemanlarını ekleme
Var olan değişkenlere elemanlar ekleme
• İki Vektörü Birleştirme ve bir vektöre yeni vektör ilave etme
Var olan değişkenlere elemanlar ekleme
• Matrise eleman ekleme
Var olan değişkenlere elemanlar ekleme
Eleman Silme
6 ıncı elemanı siler
3-6 arasındaki tüm elemanı siler
Var Olan Diziler İçin Yerleşik (Built-in) Fonksiyonlar
A vektörünün uzunluğunu verir
A matrisinin boyutunu verir
A matrisinin elemanlarından mxn tipinde
yeni bir matris oluşturur.
Var Olan Diziler İçin Yerleşik (Built-in) Fonksiyonlar
v bir vektör ise köşegen elemanları v nin
elemanları olan skaler matris oluşturur.
A bir matris ise A nın köşegen
elemanlarından oluşan bir vektör oluşturur.
Problem 1
• ones ve zeros komutlarını kullanarak aşağıdaki matrisi oluşturunuz.
VEYA
Problem 2
• ones ve zeros komutlarını kullanarak aşağıdaki matrisi oluşturunuz.
Problem 3
• Aşağıdaki matrisleri oluşturan Matlab komutlarını yazınız.
Problem 4
• Tek komutla aşağıdaki matrisleri oluşturunuz.
Problem 5
• Yukarıdaki vektör için aşağıdaki komutların ekran görüntüsü ne olur?
• Aşağıdaki komutlar çalıştırılırsa ekran görüntü ne olur?
Problem 6
• zeros, ones ve eye komutları ile aşağıdaki matrisleri oluşturunuz.
•
Tüm elemanları 1 olan 2x2 lik bir A matrisi oluşturduktan sonra matrisin kendisini
kullanarak (gerekirse birkaç kez) aşağıdaki matrisi oluşturunuz.
Diziler ve Matrislerle Matematiksel İşlemler
• Toplama ve Çıkarma
Bölme ve Matris Tersi
Bir A matrisinin tersini bulmak için inv(A)
komutu veya A^-1 komutu kullanılabilir.
/ (Sol Bölme) ve \ (Sağ Bölme)
işleçleri
VEYA
VEYA
Eleman Bazlı İşleçler
*, ^ ve /, \ işleçleri matrissel anlamda işlem yapar.
Eleman Bazlı İşleçler
*
Matris Anlamında Çarpma
.*
Eleman eleman çarpma
^
Matris Anlamında Üs Alma (A^2=A*A)
.^
Eleman eleman üs alma
/
Matris Anlamında Sol Bölme
./
Eleman eleman sol bölme
\
Matris Anlamında Sağ Bölme
.\
Eleman eleman sağ bölme
Eleman Bazlı İşleçler
fonksiyonunun x=1,2,…,8 için değerlerini hesaplayınız.
fonksiyonunun x=1,3,5,7,9,11 için değerlerini hesaplayınız.
Matlabde yerleşik matematik fonksiyonları eleman bazlı çalışırlar.
Dizi Analizleri için Yerleşik Fonksiyonlar
Fonksiyon
Görevi
C=mean(A)
A bir vektör ise C, A nın elemanlarının ortalama
değeridir. A bir matris ise C, A nın her sütunun
ortalama değerlerinden oluşan bir satır vektördür.
C=max(A)
A bir vektör ise C, A daki en büyük elemandır. A bir
matris ise C, A nın her sütununun en büyük
elemanlarından oluşan bir satır vektördür.
[d,n]=max(A)
A bir vektör ise d, A daki en büyük eleman, n ise en
büyük elemanın indis numarasıdır. A bir matris ise d,
A nın her sütunun en büyük elemanından oluşan satır
vektör, n ise en büyük elemanların sütundaki yerine
gösteren satır vektördür.
C=min(A)
C=max(A) ile aynıdır. En büyük eleman yerine en
küçük eleman için çalışır.
[d,n]=min(A)
[d,n]=max(A) ile aynıdır. En büyük eleman yerine en
küçük eleman için çalışır.
Örnek
Dizi Analizleri için Yerleşik Fonksiyonlar
Fonksiyon
Görevi
C=sum(A)
A bir vektör ise C, A nın elemanlarının toplamıdır. A
bir matris ise C, A nın her sütunundaki elemanların
toplamından oluşan bir satır vektördür.
C=sort(A)
A bir vektör ise C, A nın elemanlarının sıralı
(küçükten büyüğe) halidir. A bir matris ise C, A nın
her sütunun sıralı halidir.
C=median(A)
A bir vektör ise C, A daki elemanların medyan
değeridir. A bir matris ise her sütunun medyan
değerinden oluşan bir satır vektördür.
C=std(A)
A bir vektör ise C, A daki elemanların standart
sapmasıdır. A bir matris ise her sütunun standart
sapmasından oluşan bir satır vektördür.
Örnek
Dizi Analizleri için Yerleşik Fonksiyonlar
Fonksiyon
Görevi
det(A)
A kare matrisinin determinantı
dot(a,b)
a ve b vektörlerinin skaler çarpımı (iç çarpımı)
cross(a,b)
a ve b vektörlerinin vektörel çarpımı
inv(A)
A kare matrisinin tersini verir.
Örnek
Rasgele (Random) Sayı Üretme
Komut
Görevi
rand
0 ile 1 arasında rasgele bir sayı üretir.
rand(m,n)
Tüm elemanları 0 ile 1 arasında rasgele sayı olan
mxn boyutunda bir matris üretir.
rand(n)
Tüm elemanları 0 ile 1 arasında rasgele sayı olan
nxn boyutunda bir kare matris üretir.
randperm(n)
1 ve n arasındaki tam sayıların rasgele diziliminden
(permütasyonundan) oluşan bir vektör oluşturur.
Örnek
a ile b arasında rasgele sayı nasıl üretirsiniz?
Düzgün dağılmış rasgele sayı üretme (randi)
Komut
Görevi
randi(imax)
1 ve imax arasında rasgele bir sayı üretir.
(imax bir tamsayıdır)
randi(imax,n)
1 ve imax arasında rasgele sayılardan oluşan nxn
tipli bir matris üretir.
randi(imax,m,n)
Tüm elemanları 0 ile 1 arasında rasgele sayı olan
mxn boyutunda bir kare matris üretir.
Yukarıdaki komutlarda imax
yerine [imin imax] kullanılırsa
imin ile imax arasında sayılar
üretilir.
Örnek
Normal dağılmış rasgele sayı üretme (randn)
Normal standart dağılımda ortalama 0, varyans ise 1 dir.
rand(m,n) komutu 0 ortalamalı, 1 varyanslı normal dağılmış sayılardan
oluşan mxn boyutunda rasgele bir matris oluşturur.
50 ortalamalı, 6 varyanslı normal dağılmış sayılardan oluşan bir matris nasıl
oluşturursunuz?
Normal dağılmış tamsayı üretmek
Problem 7 (Vektörlerin Toplanması)
Şekilde gösterilen bir dirseğe üç kuvvet etki etmektedir. Dirseğe etki eden
net kuvveti bulunuz?
Bir kuvvet bir vektördür (yönü ve büyüklüğü olan fiziksel bir niceliktir).
Kartezyen koordinat sisteminde iki boyutlu bir F vektörü
clear
F1M=400; F2M=500; F3M=700;
Th1=-20; Th2=30; Th3=143;
F1=F1M*[cosd(Th1) sind(Th1)];
F2=F2M*[cosd(Th2) sind(Th2)];
F3=F3M*[cosd(Th3) sind(Th3)];
Ftot=F1+F2+F3;
FtotM=sqrt(Ftot(1)^2+Ftot(2)^2);
Th=atand(Ftot(2)/Ftot(1));
şeklinde yazılabilir.
F : Kuvvetin büyüklüğü
: Kuvvetin x ekseni ile yaptığı açı
Eğer Fx ve Fy bilinirse F ve belirlenebilir.
Dirseğe etki eden toplam kuvvet, dirseğe etki eden kuvvetlerin toplamıdır.
Buna göre aşağıdaki üç adımı takip ederek, çözümün matlab kodunu
yazınız.
• Her kuvveti iki elemanlı bir vektör olarak yaz. Vektörün ilk elemanı
vektörün x bileşeni, ikinci elemanı ise vektörün y bileşeni olacaktır.
• Vektörleri toplayarak toplam vektörünü oluştur.
• Toplam vektörünün büyüklüğü ve yönünü bul.
Problem 8 (Eleman Eleman Hesaplama)
m
F
Sürtünme ( )
Sürtünme katsayısı bir kütleyi hareket ettirmek için uygulanması gereken
kuvvetin ölçüsüyle belirlenebilir. Eğer m kütleli bir cismi hareket ettirmek
için uygulanması gereken kuvve F ise
formülü hesaplanır. Buna göre aşağıda verilen kütle ve kuvvet
değerlerine göre sürtünme katsayısını ve bu katsayıların ortalamasını
hesaplayan matlab komutlarını yazınız.
Problem 9 (Lineer denklem sistemi çözme)
Şekildeki elektrik devresinde dirençler ve voltaj kaynakları gözükmektedir. Kirchoff’un
Voltaj Kanunu üzerine kurulan ızgara akım yöntemine (mesh current method) kullanarak
herbir direnç üzerindeki akımı belirleyen matlab script dosyasını yazınız.
Kirchoff’un Voltaj Kanunu: Kapalı bir devre üzerindeki toplam voltaj sıfırdır.
Izgara akım yöntemine göre, ilk olarak her bir ızgara için bir akım (i1, i2, i3, i4) belirlenir.
Kirchoff Kanunu her bir ızgara için uygulanırsa, akımlar için bir lineer denklem sistemi elde
edilir.
İki ızgaraya ait bir dirençteki akım, ilgili ızgaralardaki akımların toplamıdır. O halde bütün
akımların aynı yönde olduğunu varsaymak uygundur.
O halde problemdeki 4 ızgara için denklemler:
Problem 10 İki Parçacığın Hareketi
Bir tren ve bir otomobil bir geçide yaklaşmaktadır. Tren geçidin güneyinden
400 ft uzaklıkta sabit 54mi/h hızla kuzeye doğru, otomobil ise geçidin
batısından 200 ft uzaklıkta 28mi/h hız ve 4 ft/s^2 ivme ile doğuya doğru
gitmektedir. Gelecek 10 saniye için tren ve otomobilin pozisyonlarını,
aralarındaki mesafeyi, otomobilin hızını, trenin otomobile göre hızını 11x6
lık bir matriste saklayan ve ekrana yazan matlab komutlarını yazınız.
Sabit bir ivmeyle düz bir çizgi boyunca hareket eden bir parçacığın konum
denklemi
ile verilir.
Problemler
1) Aşağıda verilen fonksiyonların, verilen noktalardaki değerlerini bulan matlab komutlarını yazınız.
2)
vektörü yönündeki birim vektör
olduğunu biliyoruz. Buna göre
yönündeki birim vektörü tanımlayan matlab komutunu yazınız.
3)
olduğunu gösteriniz. Bunu göstermek için x= 1.5, 1.0, 0.5, 0.1, 0.01, 0.001, 0.0001 vektörünü ve buna
karşılık y=sinx/x değerlerinden oluşan y vektörünü oluşturunuz.
4)
5)
serisinin 1 e yakınsadığını n=10, n=20, n=30, n=40 için seri değerlerini hesaplayarak gösteriniz.
serisinin
ye yakınsadığını n=10, n=20, n=30, n=40 için seri değerlerini hesaplayarak gösteriniz.
Kaynaklar
• MATLAB ile Sembolik Analiz ders notları, Prof.Dr. Erhan ÇOŞKUN, Karadeniz Teknik
Üniversitesi
• MATLAB, An Introduction with Applications, Amos Gilat, The Ohio State University