Isı Taşınımına Giriş

BÖLÜM 6
TAŞINIMIN FİZİKSEL MEKANİZMASI
2
Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu
Newton’un soğuma yasasıyla ifade edilir.
or
Taşınımla ısı transferi dinamik viskosite μ, ısıl
iletkenlik k, yoğunluk ρ, ve özgül ısı Cp gibi
akışkan özellikleri ve akışkan hızına, V bağlıdır.
:yüzeydeki sıcaklık gradyanı
3
ÖRNEK 6.1
Yerel ve ortalama taşınım katsayısının değişimi
Hız (Hidrodinamik) sınır tabaka
Bir düz levha üzerindeki akış bölgesi δ ile gösterilen hız sınır tabakası ile
sınırlandırılır.
8







Birim yüzeydeki sürtünme kuvvveti kayma
gerilmesi olarak adlandırılır ve τ ile gösterilir.
Birçok akışkan için kayma gerilmesi hız
gradyanı ile orantılı değişmektedir.
Bu sıvılar için, yüzeydeki kayma gerilmesi
aşağıdaki gibi ifade edilebilir.
Yukarıdaki doğrusal ilişkiye uyan akışkanlar
Newton tipi akışkanlar olarak adlandırılır.
Bir akışkanın viskositesi deformasyona
gösterdiği direncinin ölçüsüdür.
Sıvıların viskositesi sıcaklıkla azalırken, gazların
viskositesi sıcaklıkla artar.
Yüzey kayma gerilmesi ve sürtünme kuvveti:
9
ISIL SINIR TABAKA
Isıl Sınır Tabaka: yüzey normali yönündeki sıcaklık değişiminin önemli olduğu,
yüzey üzerindeki akış bölgesi.
Yüzey boyunca herhangi bir yerdeki ısıl
sınır tabaka kalınlığı δt,T - Ts sıcaklık
farkının 0.99 (T∞ - Ts) ’e eşit olduğu yerin
yüzeyden uzaklığı olarak tanımlanır.
Isıl sınır tabaka kalınlığı, akış yönünde
artar. Bunun sebebi, ısı transfer etkisinin
akış yönünde azalmasıdır.
10
Prandtl Sayısı (Pr)
Bir akışkanın Prandtl sayısı 0.01 değerinden (sıvı metallerde) 100,000 den daha
büyük değerlere (ağır metallerde) kadar değişmektedir. Su için Prandtl sayısı
yaklaşık 10 mertebesindedir.
11
Laminer akış ─ akış
düzgün akım çizgileri
ve son derece düzgün
hareketle
karekterize edilir.
 Türbülanslı akış ─
akış hız
dalgalanmalarıyla
 ve son derece
düzensiz hareketle
 karekterize edilir.
laminerden türbülanslı
akıma geçiş aniden
olmaz.

12


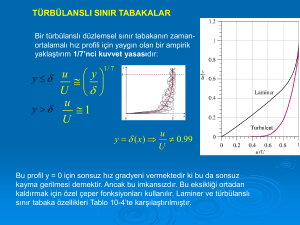
Türbülanslı akıştaki hız profili yüzey civarındaki ani düşüşle, laminer
akıma göre daha doludur.
Türbülanslı sınır tabaka dört bölgeden oluştuğu düşünülebilir :
• Viscous alttabaka
• Tampon tabaka
• Overlap tabakası
• Türbülanslı tabaka

Türbülanslı akışta yoğun karışım, ısı ve momentum transferini artırır.
13






Laminerden türbülansa geçiş yüzey geometrisi, yüzey pürüzlüğü,
akış hızı, yüzey sıcaklığı ve akışkan türüne bağlıdır.
Akış rejimi akışkandaki atalet kuvvetinin viskoz kuvvetine oranına
bağlıdır.
Bu oran Reynolds sayısı, olarak adlandırılır ve dış akış için aşağıdaki
gibi ifade edilir:
Yüksek Reynolds sayılarında (türbülanslı akış) atalet kuvveti viskoz
kuvvetlere göre göreceli olarak daha büyüktür.
Düşük Reynolds sayılarında (laminer akış), viskoz kuvvetler
büyüktür ve bu kuvvetler akıştaki çalkantları önler.
Kritik Reynolds sayısı ─ Akışın türbülanslı olduğu Reynolds sayısı
14
Bir düz levha üzerinde hız (hidrodinamik)
sınır tabakanın gelişimi
Hız sınır tabaka kalınlığı
Ortalama yüzey sürtünme katsayısı
Yerel Nusselt sayısı
Isıl sınır tabaka kalınlığı
Reynold analojisi
Düzeltilmiş Reynold analojisi
17
İki boyutlu hız sınır tabakası içindeki bir
kontrol hacmi için normal ve kayma
sürtünme gerilmeleri
İki boyutlu hız sınır tabakası içindeki bir
kontrol hacmi için momentum akıları
İki boyutlu ısıl sınır tabaka içindeki bir
kontrol hacmi için enerjinin korunumu




Elde edilen korunum denklemlerinin (süreklilik, momentum ve
enerji) analitik çözümleri zordur.
Çoğu kez denklemlerinin basitleştirilmiş biçimleriyle çalışılır.
Genellikle akışkanın sıkıştırılamaz (ρ sabit ve sabit özelliklere
sahip olduğu, gövde kuvvetleri (X=Y=0) ve enerji üretiminin
olmadığı varsayılır.
Bunlara ek olarak, sınır tabaka kabulleri olarak bilinen
basitleştirmeler yapılır. Sınır tabaka kalınlıkları genellikle çok
küçüktür ve aşağıdaki kabuller yapılabilir.

Basitleştirmeler ve yaklaşımlar ışığında, süreklilik ve xmomentum denklemi:

Sınır tabaka kabulleri ile, y momentum denklemi:

Benzer şekilde enerji denklemi:
Sürtünme kayıpları terimi ihmal edildiğinde,
sıkıştırılamaz, kararlı ve laminer akış için korunum
denklemleri:
Sınır koşulları:
Sınır tabaka denklemleri aşağıda tanımlanan boyutsuz
parametreler ile boyutsuzlaştırılabilir.
Böylece korunum denklemleri:
Sınır koşulları:
Denklemlerin boyutsuzlaştırılmasındaki asıl amaç, elde
edilecek bağımlı değişkenlerin bağlı olacakları bağımlı
değişken sayısını azaltmaktır. Yani:
 * *
dP * 
u = f1  x , y , Re L , * 
dx 

*
Eğer hız dağılımı biliniyorsa, yüzeydeki kayma gerilmesi:
∂u
τs = µ
∂y
y =0
 µV
=
 L
 ∂u
 *
 ∂y
*
y* =0
τs
2 ∂u *
=
Cf =
2
ρV / 2 Re L ∂y *
Böylece,
∂u
∂y *
*
y* =0
y* =0
 *
dP * 
= f 2  x , Re L , *  ve
dx 

 *
2
dP * 
Cf =
f 2  x , Re L , * 
Re L 
dx 
Korunum denklemlerinin çözülmesiyle boyutsuz sıcaklık
aşağıdaki parametrelere bağlıdır.
*


dP
*
*
*
T = f 3  x , y , Re L , Pr, * 
dx 

Taşınım katsayısının tanımından:
k f  T∞ − Ts  ∂T *
k f ∂T *
 * y* =0 = +
h = − 
L  Ts − T∞  ∂y
L ∂y *
y* =0
Nusselt sayısı:
h.L ∂T *
= *
Nu =
∂y
kf
y* =0
(
Nu = f 4 x* , Re L , Pr
hL
Nu =
= f 5 (Re L , Pr )
kf
)
Nusselt Sayısı (Nu)
Nusselt sayısı (Nu):
k : akışkanın ısı iletim katsayısı
Lc : karekteristik uzunluk.
Isı akısı (birim yüzeyden birim zamanda transfer
edilen ısı miktarı):
ve
Bir akışkan tabakasında Nu = 1 olması durumu tabakadaki ısı transferinin
sadece iletimle olmasını ifade eder.
35
Reynolds Benzeşimi
dP*/dx*=0 ve Pr=1 olması durumunda tüm
momentum ve enerji denklemleri benzerdir. Sınır
koşulları da aynı olduğundan, u*,v* ve T* çözümleri
birbirine eşittir. Dolayısıyla,
Re L
Cf
= Nu
2
Reynolds benzeşimi
Eğer Pr sayısı 1’den farklıysa:
Düzeltilmiş Reynods veya
Chilton- Colburn benzeşimi
Cf
2
= St. Pr 2 / 3 = jH
Burada St : Stanton sayısı (Nu/(Re.Pr))