E - unıverse of ali övgün

FİZK 104-202
Ders 6
Gauss Kanunu
Dr. Ali ÖVGÜN
DAÜ Fizik Bölümü
Kaynaklar:
-Fizik 2. Cilt (SERWAY)
-Fiziğin Temelleri 2.Kitap (HALLIDAY & RESNIK)
-Üniversite Fiziği (Cilt 2) (SEARS ve ZEMANSKY)
http://fizk104.aovgun.com
www.aovgun.com
1
Gauss Kanunu
Gauss kanunu:Tanım
q Kapalı bir yüzey boyunca toplam elektrik akısı, yüzeydeki
net elektrik yükünün ε0 a bölümüne eşittir.
q Gauss
kanunu Coulomb kanununa eşdeğerdir.
Gauss kanunu : Tanım
qBir yük dağılımını düşünelim
•Yüklerle kaplı hayali bir yüzeyle kuşatılmış olsun
• Hayali yüzey üzerindeki çeşitli noktalarda elektrik alana bakalım
!
E
!
E
+
q
• Hayali yüzeydeki yük dağılımını ortaya çıkarmak
için, özellikle yüzeydeki elektrik alanı ölçmemiz
gerekmektedir.
Hayali yüzey •Bunu yapmak için yük miktarı bilinen bir deneme
yükü yerleştirilir ve elektrik kuvvet ölçülür.
!
E
+
q0
! Deneme yükü
F
!
! F
E=
q0
Yük ve Elektrik Akısı
q Farklı
Dışa doğru
akı
İçe doğru
akı
yüklerin elektrik alanları
+q
+
−q
-
+ 2q
+ +
− 2q
-
-
Dışa doğru akı
İçe doğru akı
Yük ve Elektrik Akısı
qElektrik akısı
Dışa doğru
akı
+q
+ 2q
+
+ +
+q
+
Dışa doğru akı
Yüzeye uzaklık iki katına çıktığında
Yüzey alanı dört katına çıkar
Elektrik alan 1/4 olur.
Yük ve Elektrik Akısı
q
Elektrik akısının tanımı
Yüzeyde küçük bir alan üzerindeki herhangi bir nokta için, yüzeye dik
elektrik alan bileşenini ve yüzey alanı bileşenin çarpımını alırız.
Böylece yüzey boyunca toplanan bu nicelik net elektrik akısını verir.
q
Gauss kanununun nitel ifadesi
•Kapalı bir yüzey boyunca elektrik akısının dışa doğru mu yoksa içe doğru
mu olduğu ,yüzeyi kaplayan yükün işaretine bağlıdır.
•Yüzeyin dışındaki yükler yüzey boyunca net elektrik akısı vermez.
• Net elektrik akısı yüzeyle kuşatılmış olan net yük miktarıyla doğru
Orantılıdır fakat bunu yanında kapalı yüzeyin boyutlarından bağımsızdır.
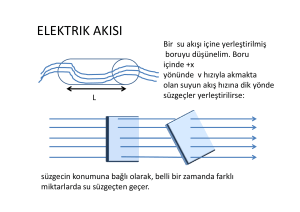
Elektrik Akısının Hesaplanması
q
Hız alan vektörü ile elektrik akı arasındaki analoji
Akan sıvı içindeki hız alan vektörü ve elektrik akı arasında iyi bir anoloji
kurulabilir.
A (alan)
Hacim akış oranı:
!
dV
≡ υA
dt
! υ Hız vektörü (akış hızı)
A Alan düzlemini belirten bir vektör alan,
düzleme diktir.
!
A
φ
A⊥
υ⊥
Hacim akış oranı:
!
υ
! !
dV
= υA cos φ = υ ⊥ A = υ ⋅ A
dt
= υA⊥
!
!
υ ⊥ = υ cos φ ; A⊥ = A cos φ ; A = An
Elektrik Akısının Hesaplanması
q Hız
alan vektörü ile elektrik akı arasındaki analoji
A (area)
Hacim akış oranı:
dV
≡ υA
dt
Elektrik akısı:
Φ E = EA
!
E
Hız vektörü (akış hızı)
!
A Bir alanın düzlemini tanımlayan vektör alan düzleme
diktir.
!
A
φ
!
E
Elektrik akı:
! !
dV
= υA cos φ = υ ⊥ A = υ ⋅ A
dt
! !
Φ = EA cos φ = E⊥ A = E ⋅ A
E⊥ = E cosφ ; A⊥ = A cosφ
Elektrik Akısının Hesaplanması
q
Küçük bir alan unsuru ve Akı
! !
dΦ E = E ⋅ dA
q
Bir alan için toplam akı
! ! ! !
Φ E = ∫ dΦ E = ∫ E⊥ dA = ∫ E cosφ dA = ∫ E ⋅ dA ; dA = ndA
qÖrnek 22.1: Bir disk boyunca elektrik akısı
r = 0.10 m !
2
2
A
=
π
(
0
.
10
m)
=
0
.
0314
m
A
φ = 30°
!
E
Φ E = EA cos φ = (2.0 ×103 N/C)(0.0314 m 2 ) cos 30°
= 54 N ⋅ m 2 / C
Elektrik Akısının Hesaplanması
q
n̂3
Örnek 22.2: Bir küp boyunca elektrik akısı
n̂5
!
E
n̂2
n̂1
n̂4
n̂6
L
!
Φ E1 = E ⋅ nˆ1 A = EL2 cos180° = − EL2
!
Φ E2 = E ⋅ nˆ2 A = EL2 cos 0° = + EL2
Φ E3 = Φ E4 = Φ E5 = Φ E6 = EL2 cos 90° = 0
Φ E = ∑i =1 Φ Ei = 0
i =6
Elektrik Akısının Hesaplanması
qÖrnek 22.3: Bir küre boyunca elektrik akısı
!
dA
r=0.20 m
+
+q
!
!
E⊥ = E , E // nˆ // dA
−6
3
.
0
×
10
C
9
2
2
E=
=
(
9
.
0
×
10
N
⋅
m
/
C
)
4πε 0 r 2
(0.20m)2
q
= 6.75 × 10 5 N/C
Φ E = ∫ EdA = EA = (6.75 ×10 5 N/C)(4π )(0.20m) 2
q=3.0 µC
A=2πr2
= 3.4 × 10 5 N ⋅ m 2 / C
Gauss kanunu
q
Öncelikle :
Herhangi bir kapalı yüzey boyunca toplam elektrik akısı (belirli bir hacimle
kaplanan yüzey) yüzeydeki toplam elektrik yüküyle orantılıdır.
q
Durum 1: Bir tek pozitif q yükünün alanı
!
E
r=R olan bir küre
r=R
+
+q
!
E
q
at r=R
2
4πε 0 R
1 q
q
Φ E = EA =
(4πR 2 ) =
4πε 0 R
ε0
E=
1
Akı R yüzey yarıçapından bağımsızdır .
!
E ⊥ surface
Gauss Kanunu
q
Durum1: Bir tek pozitif q yükünün alanı
!
1 !
E2 R = E R
4
dA2 R = 4dA
r=R
+
+q
r=2R
!
ER
dAR = dA
Küçük bir küreden geçen her alan çizgisi aynı
zamanda daha büyük bir küreden de geçer
Her bir küre boyunca toplam akı
aynıdır.
Benzerlik dA gibi yüzeyin her bir parçası
için doğrudur.
dΦ ER = ER dAR =
1
ER 4dAR = E2 R dA2 R = dΦ E2 R
4
! ! q
Φ E = ∫ E ⋅ dA =
ε0
Yükü kaplayan kapalı yüzeyi sağlayan her boyut veya her
şekil için bu doğrudur.
Gauss Kanunu
q
Durum 2: Bir tek pozitif yükün alanı (Genel yüzey)
!
E
dA
! !
E⊥ = n ⋅ E
!
E dA
= E cos φ
φ
dA cosφ
!
+
+q
+
Yüzeye dik E
dΦE = E⊥dA = E cosφdA
! ! q
Φ E = ∫ E ⋅ dA =
ε0
Gauss kanunu
qDurum 3: İçinde yük bulunmayan kapalı bir yüzey
! !
Φ E = ∫ E ⋅ dA = 0
İçeri giren elektrik alan çizgileri, dışarı çıkar.
Elektrik alan çizgilerinin alanın bir bölgesinde
başlayabilmesi ya da bitebilmesi ancak o bölge
içinde yük mevcutken olur.
+
q
Bir başka örnek 22.4
Gauss kanunu
! ! Qencl
!
!
Φ E = ∫ E ⋅ dA =
; Qencl = ∑i qi , E = ∑i Ei
ε0
Kapalı yüzey boyunca toplam elektrik akı yüzey içindeki net elektrik yükünün
ε0 a bölümüne eşittir
Gauss kanununun uygulamaları
q
Tanım
• Yük dağılımı
Alan
• Simetri uygulamanın prosedürünü kolaylaştırır.
q
Bir iletken üzerindeki yük dağılımını elektrik alanı
• Fazla yük katı iletken üzerine yerleşmişken ve sabitken,
tamamen yüzeyde bulunur, bu metalin iç yükü değildir.
(fazla yük = metali iletken yapan serbest elektron ve iyonlar dışındaki yüktür.)
İletken içindeki gauss yüzeyi
Yüzeydeki yük
iletken
Gauss kanununun uygulamaları
qİletken üzerindeki yük dağılımının elektrik alanı
İletken içindeki gauss yüzeyi
Yüzeydeki yükler
İletken
İletken metal içerisinde her noktadaki elektrik alan
bir elektrostatik konumda sıfırdır. (bütün yükler hareketsizdir
Şayet E sıfır olmasaydı, yükler hareket ederdi.
•İletken içerisindeki gauss yüzeyi çizilir
• Bu yüzeyde her yerde E=0 dır (iletken içinde)
Gauss kanunu
• Yüzey içindeki net yük sıfırdır.
• Katı iletken içerisinde herhangi bir noktada hiçbir fazla yük olmayabilir.
• Her bir fazla yük iletken yüzeyinde bulunmalıdır.
• Yüzeydeki E yüzeye diktir.
Sayfa 84 deki problem çözüm stratejisini okuyun
Gauss kanununun uygulamaları
qörnek 22.5: Yüklü iletken kürenin alanı
Gauss yüzeyi
+
+
+
1
q
4πε 0 R 2
ER / 4
ER / 9
R<r:
+
R
+
ER =
+
!
r < R: E =0
+
Küre dışında bir Gauss yüzeyi
çizilir
+
R
2R
3R
1
q
r = R: E =
4πε 0 R 2
Gauss kanununun uygulamaları
q
Örnek 22.6: Çizgi yükün alanı
!
Simetriye göre seçilen Gauss yüzeyi
E , E⊥ = E !
dA
Çizgi yük
yoğunluğu
Qencl = !λ
λ!
Φ E = E (2π r!) =
ε0
1 λ
E=
2πε 0 r
Gauss kanununun uygulamaları
qÖrnek 22.7: Yüklü sonsuz düzgün bir levhanın alanı
!
E
+ +
+
+
+
+ +
+
+ +
+
Gauss yüzeyi
!
E
Qencl = σA
İki sonlu yüzey
σA
Φ E = 2( EA) =
ε0
σ
E=
2ε 0
Gauss kanununun uygulamaları
q
Örnek 22.8: Zıt yüklü paralel iletken plakalar arasındaki alan
! ! plate 1 !
E1 E 2
+ b E1
!
+
a
E2
+
S1 +
+
+
+
S2
+
+
!
E
plate 2 ! !
- E 2 E1
c
- S4
S3
-
Çözüm 1:
Dışa doğru akı
İçe doğru akı
Çözüm 2:
!
!
! ! ! !
Noktada a : E1 = − E2 → E = E1 + E2 = 0
Bu yüzeyler üzerinde
!
!
!
b : E1 = E2 → E = 2 σ = σ
elektrik akı yok
2ε 0 ε 0
!
!
! ! ! !
c : E1 = − E2 → E = E1 + E2 = 0
Gauss kanununun uygulamaları
qÖrnek 22.9: Düzgün bir şekilde yüklü kürenin alanı
Gauss yüzeyi
+
+
+
+
+ +
+r=R
+
+
+
+
+
R
4 3
r < R : EA = ρ ( π r ) / ε 0
3
4
2
E (4π r ) = ρ ( π r 3 ) / ε 0
3
1 Qr
→E=
4πε 0 R 3
1 Q
r = R: E =
4πε 0 R 2
Q
2
R < r : E (4π r ) =
ε0
1 Q
→E=
4πε 0 r 2
Gauss kanununun uygulamaları
qÖrnek 22.10: Yüklü içi boş kürenin alanı
r=0.300 m
!
E
E = 1.80 ×10 2 N/C
E⊥ = − E
Φ E = ∫ E⊥ dA = − E (4π r 2 ) =
R=0.250 m
İçi boş yüklü küre
q
ε0
q = − E (4πε 0 r 2 ) = −0.801 nC
Gauss yüzeyi
İletkenler üzerindeki yükler
Durum 1: Katı iletken üzerindeki yük elektrostatik bir durumdaki
İletken yüzeyinde bulunur.
q
+ + +
+
+
+
+
+
+ ++
+
++
+ +
İletken içerisinde her noktada elektrik alan sıfırdır ve
Katı iletken üzerindeki her bir fazla yük
onun yüzeyi üzerine yerleşir.
qDurum 2: Oyulmuş iletken üzerindeki yük
+ + +
+
+
+
+
+
+ ++
+
++
+ +
Oyuk içinde yük yoksa, oyuk yüzey üzerindeki net
yük sıfırdır.
Gauss yüzeyi
İletkenler üzerindeki yükler
qDurum 3: Oyuklu bir iletkenin yükü ve oyuk içindeki q yükü
+ + +
+
+
- - +
+
- +
- +
+
- - +
+ ++
+
++
Gauss yüzeyi
•İletken yüklenmemiştir ve q yükünden yalıtılmıştır.
•Gauss yüzeyindeki toplam yük Gauss kuralı ve yüzeyde
E=0 olduğundan sıfır olmalıdır.Bu yüzden boşluğun
yüzeyinde yüzeye dağılmış –q yükü olmalıdır
•Benzer tartışma başlangıçta qC yüküne sahip iletken
durumu için kullanılabilir.Bu durumda dış yüzeydeki
toplam yük oyuk içine koyulan q yükünden sonra
q+qC olmalıdır
İletkenler üzerindeki yükler
q
Faraday ın buz kovası deneyi
Yüklü iletken top
iletken
(1) Faraday yüksüz metal buz kovası(metal kova) ve yüksüz elektroskop ile işe
başladı
(2) Daha sonra, dikkatli bir şekilde kovanın yanlarına dokundurmadan buz kova
içerisine metal topu sarkıttı. Elektroskop’ un yaprakları ayrıldı.
Bununla birlikte, ayrılma derecesi metal topun yerleşiminden bağımsızdır. Sadece metal
top tamamen geri çekildiğinde yaprakları eski pozisyonuna geri döner.
İletkenler üzerindeki yükler
q
Faraday ın buz kovası deneyi
Yüklü iletken top
iletken
(3) Faraday şayet metal topun buz kovanın yüzeyi içine kontak etmesine müsaade
edilseydi elektroskop’un yapraklarının ayrı kalacağına dikkat çekti.
(4) Daha sonra , buz kova içerisinden topu tamamen çıkardığında, yapraklar ayrı
kaldı. Bununla birlikte, metal top artık yüksüzdür.
Bunun için küreye dıştan bağlı olan elektroskobun yaprakları, top kürenin içerisine
dokundurulduğunda, hareket etmedi , böylece Faraday topu nötürleştirmek için iç
yüzeyin yeterince yüke sahip olduğunu buldu.
İletkenler üzerindeki yükler
q
•
Bir İletken yüzeyindeki alan
İletken dışındaki elektrik alanın büyüklüğü σ /ε0
dır ve yüzeye dik yönlendirilmiştir.
İletken içine ilerleyen küçük bir hap kutu çizilir.
içerde alan olmadığı için , bütün akılar üst
taraftan çıkar.
EA=q/ε0= σA/ ε0,
E= σ / ε0
Alıştırmalar
q Alıştırma
1
Alıştırmalar
q Alıştırma 1
Alıştırmalar
qAlıştırma 2: Bir küre ve bir iletken kabuk
Q2=-3Q1
Q2
• Gauss kanunundan iletken içerisinde net yük olmaz,
ve yük küre yüzeyi dışında bulunmalıdır.
Q1
R1
R2
• Küre içinde net yük olmaz.
Bu yüzden kabuk yüzeyine –Q1 net yükü götürülmelidir ve
yüzeyin dışına +Q1+Q2 net yükü götürülmelidir. Böylece
kabuk üzerinde net yük Q2 ye eşittir. Bu yükler düzenli
bir şekilde dağılır.
σ inner
Q1
=−
4πR22
σ outer
Q2 + Q1 − 2Q1
=
=
2
4πR2
4πR22
Alıştırmalar
qAlıştırma 2: Bir küre ve bir iletken kabuk
Q2=-3Q1
Q2
r < R1 :
Q1
R1
R2
R1 < r < R2 :
R2 < r :
!
E=0
!
Q1
E = k 2 rˆ
r
!
Q1 + Q2
2Q1
E=k
rˆ = −k 2 rˆ
2
r
r
Alıştırmalar
qAlıştırma 3: Silindir
Sonsuz bir çizgi yük yarıçapı R olan içi boş yüklü iletken sonsuz bir
silindiriksel kabuğun tam olarak ortasından geçer. Şimdi uzunluğu h olan
silindirik kabuğun bir parçasına odaklanalım. Çizgi yük λ lineer yük
yoğunluğuna sahiptir, ve silindirik kabuk σtotal yüzey yük yoğunluğuna
sahiptir.
σtoplam
λ
R
σiç
σdış
h
Alıştırmalar
qAlıştırma 3: Silindir
Silindirik kabuk içinde elektrik alan sıfırdır. Bu yüzden silindirde silindir kabuk
içinde bulunan bir gauss yüzeyi seçersek , kuşatılmış net yük sıfır olur. Çizgi
boyunca dış yükü dengelemek için silindir duvar içinde bir yüzey yük yoğunluğu
mevcuttur.
σtoplam
λ
R
σiç
σdış
h
Alıştırmalar
q Alıştırma 3: Silindir
λh
Qinner = −λh
•Çizgi yükün kuşatılmış parçası ( h uzunluğu) üzerindeki toplam yük :
• İletken silindir kabuğun yüzeyi içindeki yük:
σ inner
λ
− λh
λ
=
=−
2πRh
2πR
σtoplam
R
σiç
σdış
h
Alıştırmalar
q Alıştırma 3: Silinidir
σ total
• Silindir üzerindeki net yük yoğunluğu:
•Harici yük yoğunluğu :
σ outer = σ total − σ inner
λ
σ outer
λ
= σ total +
2πR
σtoplam
R
σiç
σdış
h
Alıştırmalar
q Alıştırma 3: Silindir
• r (>R) yarıçaplı çizgi yükle çevrelenen Gauss yüzeyini çizelim;
2πrhEr =
qencl
ε0
, qencl
λ
= λh → Er =
for r < R
2πε 0 r
σtotal
λ
R
σiç
σdış
h
Alıştırmalar
qAlıştırma 3: Silindir
•r (>R) yarıçaplı çizgi yükle çevrelenen Gauss yüzeyini çizelim;
•Çizgi üzerindeki net yük:
2πrhEr =
λ
qencl
ε0
λh
kabuk boyunca net yük:
, qencl = Q + λh → Er =
σiç
σdış
σ total R
λ
+
for r > R
ε 0 r 2πε 0 r
σtotal
R
h
Q = 2πRhσ total