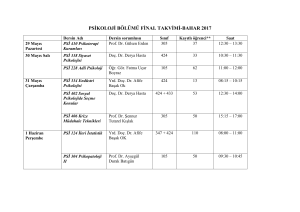
MATLAB ile Sembolik
Analiz
SERİLER
SERİLER
Sembolik Toplama
symsum(f) VEYA symsum(f,var) VEYA syssum(f,var,a,b)
symsum(f,var) : f ile tanımlanan bir serinin terimlerini, var isimli değişkene göre toplar. Değişken
değerleri 0 dan (var-1)’e değişir. Eğer var değişkeni belirtilmez ise varsayılan değişkene göre işlemler
yapılır.
n−1
n−1
𝑘
𝑘=1
>> syms k
>> symsum(k) % VEYA symsum(k,k)
ans =
k^2/2 - k/2
𝑘=1
1
𝑘2
>> syms k
>> symsum(1/k^2)
ans=
-psi(1, k)
𝑑
𝑝𝑠𝑖 𝑥 = 𝑑𝑖𝑔𝑎𝑚𝑚𝑎 𝑥 =
ln Γ 𝑥
𝑑𝑥
𝑑
Γ 𝑥
𝑑𝑥
=
Γ 𝑥
psi(n,x): psi fonksiyonunun n-türevidir. psi(0,x) digamma
(poligamma), psi(1,x) trigamma, psi(2,x) tetragamma
fonksiyonudur.
Sembolik Toplama
symsum(f) VEYA symsum(f,var) VEYA syssum(f,var,a,b)
symsum(f,var,a,b) : f ile tanımlanan bir serinin terimlerini, var isimli değişkene göre toplar. Değişken
değerleri a dan b’ye değişir. Eğer var değişkeni belirtilmez ise varsayılan değişkene göre işlemler yapılır.
∞
10
𝑘
𝑘=1
𝑘=0
>> syms k
>> symsum(k^2, 0, 10)
ans =
385
∞
𝑥𝑘
𝑘=0
1
𝑘2
>> syms k
>> symsum(1/k^2,1,inf)
ans=
pi^2/6
∞
𝑘=0
𝑥𝑘
𝑘!
>> syms k x
>> symsum(x^k/sym('k!'), k, 0, Inf)
ans =
exp(x)
>> syms k x
>> s2 = symsum(x^k, k, 0, inf)
s2 =
piecewise([1 <= x, Inf], [abs(x) < 1, -1/(x - 1)])
Taylor Serisi
taylor(f)
f yi , 5. dereceye kadar Maclaurine
serisine açar.
taylor(f,v)
f nin, v ye göre seri Maclaurine seri açılımı
taylor(f,v,a)
f nin, v ye göre a noktasındaki Taylor seri
açılımı
>> syms x
>> taylor(exp(x))
ans =
x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1
>> syms x
>> taylor(sin(x))
ans =
x^5/120 - x^3/6 + x
>> syms x
>> taylor(cos(x))
ans =
x^4/24 - x^2/2 + 1
Taylor Serisi
taylor(f,özellik_1,değer_1,özellik_2,değer_2,…,özellik_n,değer_n)
>> syms x
>> taylor(log(x), x, 'ExpansionPoint', 1) % VEYA taylor(log(x),x,1)
ans=
x - (x - 1)^2/2 + (x - 1)^3/3 - (x - 1)^4/4 + (x - 1)^5/5 - 1
>> syms x
>> f = sin(x)/x;
>> t6 = taylor(f)
t6=
x^4/120 - x^2/6 + 1
>> t8 = taylor(f, 'Order', 8)
t8 =
- x^6/5040 + x^4/120 - x^2/6 + 1
>> t10 = taylor(f, 'Order', 10)
t10 =
- x^8/362880 - x^6/5040 + x^4/120 - x^2/6 + 1
Örnek
plotT6 = ezplot(t6, [-4, 4]);
hold on
set(plotT6,'Color','red')
sin(x)/x için Taylor Seri Açılımları
1
0.8
plotT8 = ezplot(t8, [-4, 4]);
set(plotT8,'Color','magenta')
plotT10 = ezplot(t10, [-4, 4]);
set(plotT10,'Color','cyan')
plotF = ezplot(f, [-4, 4]);
set(plotF,'Color','blue','LineWidth', 2)
title(‘sin(x)/x için Taylor Seri
Açılımları')
hold off
0.6
0.4
0.2
0
-0.2
-4
-3
-2
-1
0
x
1
2
3
4
Örnek
>> syms x y z
>> f = sin(x) + cos(y) + exp(z);
>> taylor(f)
ans =
x^5/120 - x^3/6 + x + cos(y) + exp(z)
>> taylor(f, [x, y, z])
ans =
x^5/120 - x^3/6 + x + y^4/24 - y^2/2 + z^5/120 +
z^4/24 + z^3/6 + z^2/2 + z + 2
Örnek
Taylor Yaklaşımı ve Gerçek Fonksiyon
Taylor
Fonksiyon
6
>> syms x
>> g = exp(x*sin(x));
>> t = taylor(g, 'ExpansionPoint', 2, 'Order', 12);
>> xd = 1:0.05:3; yd = subs(g,x,xd);
>> ezplot(t, [1, 3]); hold on;
>> plot(xd, yd, 'r-.')
>> title('Taylor Yaklaşımı ve Gerçek Fonksiyon');
>> legend('Taylor',‘Fonksiyon')
5
4
3
2
1
1
1.2
1.4
1.6
1.8
2
x
2.2
2.4
2.6
2.8
3
Taylortool
taylortool veya taylortool(f)
Taylor Series Approximation
20
10
0
-10
-20
-10
-5
0
5
10
TN(x) = x - x 3/2 + x 5/24 - x 7/720 +...- x 23/1124000727777607680000
taylortool('sin(tan(x)) - tan(sin(x))')