Dinamik sistemler nasıl modellenir ?
Dinamik sistemlerin modellenmesinden kasıt, sistemlerin matematik
modelinin oluşturulmasıdır.
Dinamik bir sistemin matematik modeli, incelenen sistemin dinamik
özelliklerini belirten matematiksel
ifadeler bütünü olarak
tanımlanabilir.
Sistemlerin sadece bir tek matematik modeli yoktur. Sistemler, farklı
yöntemler kullanarak modellenebilirler (doğrusal modelleme,
doğrusal olmayan modelleme, durum değişkenleri yöntemi
kullanarak modelleme, yapay sinir ağları yardımıyla modelleme vs.)
Sistem Dinamiği ve
Modellemesi
Dinamik Sistemlerin Modellenmesi ve Analizi
2
Dinamik sistemler nasıl modellenir ?
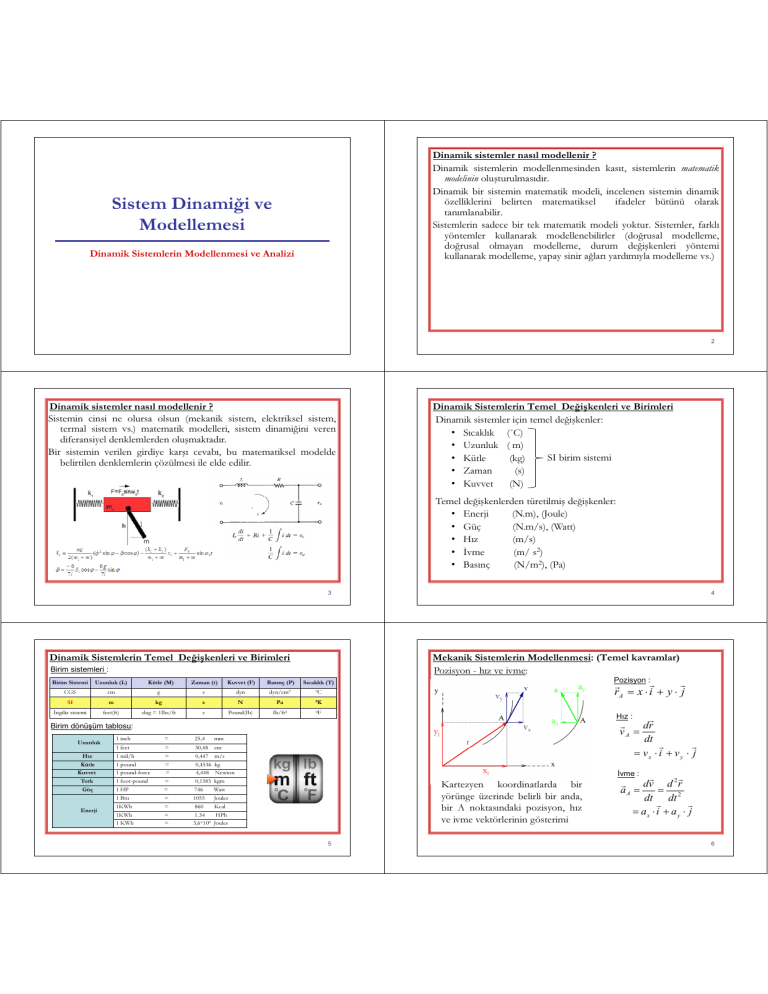
Sistemin cinsi ne olursa olsun (mekanik sistem, elektriksel sistem,
termal sistem vs.) matematik modelleri, sistem dinamiğini veren
diferansiyel denklemlerden oluşmaktadır.
Bir sistemin verilen girdiye karşı cevabı, bu matematiksel modelde
belirtilen denklemlerin çözülmesi ile elde edilir.
Dinamik Sistemlerin Temel Değişkenleri ve Birimleri
Dinamik sistemler için temel değişkenler:
• Sıcaklık (˚C)
• Uzunluk ( m)
SI birim sistemi
• Kütle
(kg)
• Zaman
(s)
• Kuvvet
(N)
Temel değişkenlerden türetilmiş değişkenler:
• Enerji
(N.m), (Joule)
• Güç
(N.m/s), (Watt)
• Hız
(m/s)
• İvme
(m/ s2)
• Basınç
(N/m2), (Pa)
3
Dinamik Sistemlerin Temel Değişkenleri ve Birimleri
Mekanik Sistemlerin Modellenmesi: (Temel kavramlar)
Pozisyon - hız ve ivme:
Birim sistemleri :
Birim Sistemi
Uzunluk (L)
CGS
cm
Kütle (M)
g
4
Zaman (t)
Kuvvet (F)
Basınç (P)
Sıcaklık (T)
s
dyn
dyn/cm2
0C
SI
m
kg
s
N
Pa
0K
İngiliz sistemi
feet(ft)
slug = 1Ibs/ft
s
Pound(Ib)
Ib/ft2
0F
Pozisyon :
r
r
r
rA = x ⋅ i + y ⋅ j
Hız :
r
r
dr
vA =
dt
r
r
= vx ⋅ i + vy ⋅ j
Birim dönüşüm tablosu:
Uzunluk
Hız
Kütle
Kuvvet
Tork
Güç
Enerji
1 inch
=
25,4
mm
1 feet
1 mil/h
1 pound
1 pound-force
1 foot-pound
1 HP
1 Btu
1KWh
1KWh
1 KWh
=
=
=
=
=
=
=
=
=
=
30,48
0,447
0,4536
4,448
0,1383
746
1055
860
1.34
3,6*106
cm
m/s
kg
Newton
kgm
Watt
Joules
Kcal
HPh
Joules
İvme :
Kartezyen koordinatlarda bir
yörünge üzerinde belirli bir anda,
bir A noktasındaki pozisyon, hız
ve ivme vektörlerinin gösterimi
5
r
r
r
dv d 2 r
= 2
aA =
dt dt
r
r
= ax ⋅ i + a y ⋅ j
6
Mekanik Sistemlerin Modellenmesi: (Temel kavramlar)
Mekanik Sistemlerin Modellenmesi: (Temel kavramlar)
Newton’un ikinci yasası :
Mekanik sistemlerin hareketi öteleme (translation), dönme (rotation) veya
bunların birleşimi şeklinde sınıflandırılır ve modelleme buna uygun
şekilde yapılır.
Hareketi ifade eden denklemler genellikle doğrudan veya dolaylı yollar
ile Newton’un ikinci yasasından türerler.
“Bir cismin momentumundaki değişim, cisim üzerine uygulanan itme ile
orantılıdır ve itmenin uygulandığı düz doğru boyunca meydana gelir.”
Ötelenen sistemler için:
Dönen sistemler için:
Fnet
Tnet =
d (m ⋅ v )
=
dt
Fnet = m ⋅
d (v )
= m⋅a
dt
Fnet
d (J ⋅ w )
dt
d (w )
=J⋅
= J ⋅α
dt
“Bir cismin ivmesi, üzerine uygulanan kuvvet ile doğru, cismin kütlesi ile
ters orantılıdır.”
7
Mekanik Sistemlerin Modellenmesi: (Temel kavramlar)
Öteleme Hareketi (Translational Motion):
Üç boyutlu uzayda rijit bir cismin x,y,z eksenlerinde doğrusal hareketi
öteleme hareketi olarak tanımlanır. Öteleme hareketinde dikkate
alınacak hareket değişkenleri çizgisel yer değiştirme, çizgisel hız ve çizgisel
ivmedir.
8
Mekanik Sistemlerin Modellenmesi: (Öteleme Hareketi)
1. Kütle :
Bir cismin değişmeyen nicel bir özelliğidir ve maddenin doğrusal
harekete karşı gösterdiği direnç miktarıdır. (Bknz. Newton
kanunları)
M =
r
r
∑F = m ⋅a
Rijit cisme etki eden
toplam kuvvet
W
g
W : cismin ağırlığı
g : yer çekimi ivmesi (m/s2)
g = 32,174 (ft/s2)
g = 9,8066 (m/s2)
Rijit cismin ivmesi
F (t ) = M ⋅ a (t ) = M ⋅
Rijit cismin kütlesi
d2y
dv
=M⋅
dt 2
dt
9
Mekanik Sistemlerin Modellenmesi: (Öteleme Hareketi)
2. Lineer Yay :
Potansiyel enerjiyi depolayan bir eleman olarak tanımlanır. Yaylar
doğrusal olmayan bir karakteristikte sahip olsalar da dar bir
çalışma alanında doğrusal kabul edilebilirler.
f (t ) = K ⋅ y (t )
10
Mekanik Sistemlerin Modellenmesi: (Öteleme Hareketi)
2. Sürtünme Etkisi:
İki fiziksel eleman arasında bir hareket olduğunda veya sistem hareket
etme eğilimi gösterdiğinde sürtünme etkisi oluşur ve bu etki
genelde doğrusal olmayan bir karakteristiktedir.
İki yüzey arasında sürtünme etkisinin oluşma nedenleri:
Birim
Yay Sabiti K
SI birim sistemi
N/m
İngiliz birim sistemi
lb/ft
yay sabiti
Yüzeylerin yapısı
Yüzeyler arası basınç oluşumu
Yüzeyler arası bağıl hız vs.
Genelde sistemlerde üç çeşit sürtünme etkisi görülür:
Yaya Fön gibi bir kuvvet ile ön
yükleme uygulanmış ise :
f (t ) − Fön = K ⋅ y (t )
11
Vizkoz sürtünme
Statik sürtünme
Coulomb sürtünmesi
12
f (t ) = B ⋅
dy
dt
Mekanik Sistemlerin Modellenmesi: (Öteleme Hareketi)
Vizkoz Sürtünme:
Uygulanan kuvvet ile hız arasındaki doğrusal ilişkidir. Sönüm elemanı
bu etkiyi oluşturan en temel elemandır.
f (t ) = B ⋅
f (t ) = ± ( Fs ) | y& =0
dy
dt
. Sürtünme etkisinin işareti, hareket
yönüne veya başlangıç hız yönüne
ters yöndedir.
Vizkoz sönüm sabiti
Hareket başladığı anda statik
sürtünme etkisi biter ve varsa
diğer sürtünme etkileri devreye
girer.
Vizkoz sönüm sabiti B
Birim
Mekanik Sistemlerin Modellenmesi: (Öteleme Hareketi)
Statik Sürtünme:
Temas halinde olan iki cisim birbirlerine göre durgun haldeyken,
oluşacak bağlı harekete karşı koyan etki.
SI birim sistemi
N.s/m
İngiliz birim sistemi
lb.s/ft
13
Mekanik Sistemlerin Modellenmesi: (Öteleme Hareketi)
Coulomb Sürtünmesi:
Hızın değişimine bağlı olarak sabit genliği olan, fakat hızın yönünün
değişimine ters yönde kuvvetin işaretinin değiştiği sürtünme etkisi
türüdür.
14
Mekanik Sistemlerin Modellenmesi: (Temel kavramlar)
Dönme Hareketi(Rotational Motion):
Üç boyutlu uzayda rijit bir cismin sabit x,y,z eksenleri etrafında yaptığı
hareket olarak tanımlanır. Dönme hareketinde dikkate alınacak
hareket değişkenleri açısal yer değiştirme, açısal hız ve açısal ivmedir.
∑ T = I ⋅α
r
r
.
f (t ) = µ c Fc ⋅ sign(
dy ((tt )
)
dt
Rijit cisme etki eden
toplam tork
Rijit cismin açısal
ivmesi
Rijit cismin ataleti
15
Mekanik Sistemlerin Modellenmesi: (Dönme Hareketi)
1. Atalet :
Bir cismin değişmeyen nicel bir özelliğidir ve maddenin dönel
harekete karşı gösterdiği direnç miktarıdır.
16
Mekanik Sistemlerin Modellenmesi: (Dönme Hareketi)
2. Torsiyon yayı :
Cismin ataleti geometriye ve hangi eksene göre ataletin
hesaplandığına göre farklılık gösterir.
Farklı geometrilere sahip cisimlerin atalet momenti değerleri
tabloda verilmiştir.
Birim
Atalet Tork Açısal yer değiştirme
SI
kg.m2
N.m
rad
İngiliz
slug.ft2
lb.ft
rad
dw(t )
d 2θ (t )
=I⋅
T (t ) = I ⋅ α (t ) = J ⋅
dt
dt 2
17
Birim
Yay Sabiti K
SI birim sistemi
N/m
İngiliz birim sistemi
lb/ft
TP ön yüklemesi uygulanırsa :
T (t ) = K θ ⋅ θ (t )
T (t ) − TP = K θ ⋅ θ (t )
3. Dönme Hareketinde Sürtünme :
dθ
dt
Vizkoz Sürtünme
: T (t ) = Bθ ⋅
Statik Sürtünme
:
T (t ) = ± (Ts ) |θ = 0
Coulomb Sürtünmesi
:
T (t ) = Tc ⋅
dθ (t ) / dt
dθ (t ) / dt
18
Mekanik Sistemlerin Hareket Denklemlerinin Çıkartılması:
Mekanik Sistemlerin İndirgenmeleri ve Eşdeğer Bağıntıları:
Örnek 1 : Şekil 1’deki sistemin hareket denklemlerini çıkartınız.(m=0 kütlesiz
farzedilecektir.)
Mekanik sistemlerin dinamik çözümlemelerinde pek çok durumda
sistemin dinamik parametreleri (kütle, atalet, yay katsayısı, sönüm
katsayısı vs.) sabit veya belirli bir noktada topaklanmış
(indirgenmiş) olarak düşünülebilir.
Örnek 2 : Şekil’de görülen ve biribirlerine bir halatla bağlı makara- kütle-yay
sisteminde, kütlenin kendisine etki eden bir F(t) kuvvetinin etkisi altında
yapacağı titreşimlerin hareket denklemini çıkarınız. (makara ile halat arasında
kayma olmadığı farzedilecektir.)
Mekanik Sistemlerde Kütle İndirgemesi :
Dağılmış parametreli bir sistem, aşağıdaki kabullerle belirli bir noktada
topaklanmış eşdeğer bir sisteme dönüştürülebilir:
Eşdeğerlik şartları:
Aynı toplam kütle
Aynı kütle atalet merkezi (veya ağırlık merkezi)
Aynı dönme atalet momenti
Şekil 1
Aynı toplam enerji veya enerji kaybı
Şekil 2
19
20
Yayılmış Kütleli bir Çubuğun Kütle ve Atalet Eşdeğeri:
Yayılmış Kütleli bir Çubuğun Kütle ve Atalet Eşdeğeri:
M
dM = ⋅ x
L
M
dM = ⋅ x
L
1
dEk = . dM .Vx2
2
1 M
dEk = . dx.( w. x ) 2
2 L
Vx = w ⋅ x
Vx = w ⋅ x
1
dEk = . dM .Vx2
2
1 M
dEk = . dx.( w. x ) 2
2 L
1
2
M A .V A =
2
L
∫ dEk
=
1 M 2 2
ω x dx ;
L
V A = ω .a
∫2
0
L
1
1 M 2
ω ∫ x 2 dx → M
M Aω 2 a 2 =
2
2 L
x=0
A
=
M L2
3 a2
21
22
Yayılmış Kütleli bir Çubuğun Kütle ve Atalet Eşdeğeri:
Yayılmış Kütleli bir Çubuğun Kütle ve Atalet Eşdeğeri:
M
dM = ⋅ x
L
M
dM = ⋅ x
L
Vx = w ⋅ x
Vx = w ⋅ x
L
L
1
1
1 M
I Oω 2 = ∫ dEk = ∫ dM .x 2 .ω 2 = ∫ . .dx.x 2ω 2
2
2
x =0
x =0 2 L
IO =
ML2
3
SORU ! Steiner Teoremi ile tekrar hesaplayınız
23
24
Çok Kütleli Sistemlerin İndirgenmesi:
Eeq = (1 / 2).M eq .Veq
Çok Kütleli Sistemlerin İndirgenmesi:
Eeq = (1 / 2).M eq .Veq
2
2
Eeq = (1 / 2).M 1.V1 + (1 / 2).M 2 .V2
2
M 1.V1 + M 2 .V2
2
Veq
2
M eq =
2
2
25
26
Bir Nokta Etrafında Dönen Rijit İki Kütlenin İndirgenmesi:
Bir Nokta Etrafında Dönen Rijit İki Kütlenin İndirgenmesi:
Eşdeğer atalet indirgemesi :
Eşdeğer atalet indirgemesi :
1
1
1
2
2
2
Eeq = .I eq .θ&eq = .I1.θ&1 + .I 2 .θ&2
2
2
2
2
2
I .θ& + I .θ&
I eq = 1 1 2 2 2
θ&
1
1
1
2
2
2
Eeq = .I eq .θ&eq = .I1.θ&1 + .I 2 .θ&2
2
2
2
2
2
I .θ& + I .θ&
I eq = I1 + I 2
I eq = 1 1 2 2 2
θ&
eq
θ&1 = θ&2 = θ&eq = w
eq
27
28
Bir Nokta Etrafında Dönen Rijit İki Kütlenin İndirgenmesi:
Bir Nokta Etrafında Dönen Rijit İki Kütlenin İndirgenmesi:
Eşdeğer kütle indirgemesi :
Eşdeğer kütle indirgemesi :
1
1
1
2
2
2
Eeq = .M eq .Veq = .M 1.V1 + .M 2 .V2
2
2
2
M 1.V1 + M 2 .V2
2
Veq
2
M eq =
1
1
1
2
2
2
Eeq = .M eq .Veq = .M 1.V1 + .M 2 .V2
2
2
2
2
M 1.V1 + M 2 .V2
2
Veq
2
M eq =
2
M eq = M 1 + M 2 .( L2 / L1 ) 2
V2 = V1.( L2 / L1 )
29
30
Dönme ve Öteleme Hareketi Yapan Sistemlerin İndirgenmesi :
Dönme ve Öteleme Hareketi Yapan Sistemlerin İndirgenmesi :
Öteleme Eşdeğeri :
Öteleme Eşdeğeri :
1
1
1
2
E = .M eq .Veq = .M .V 2 + .I .θ& 2
2
2
2
1
1
1
2
E = .M eq .Veq = .M .V 2 + .I .θ& 2
2
2
2
V
Veq = V , θ& =
R
31
32
Dönme ve Öteleme Hareketi Yapan Sistemlerin İndirgenmesi :
Dönme ve Öteleme Hareketi Yapan Sistemlerin İndirgenmesi :
Öteleme Eşdeğeri :
Dönme Eşdeğeri :
1
1
1
2
E = .M eq .Veq = .M .V 2 + .I .θ& 2
2
2
2
V
Veq = V , θ& =
R
1
1
1
.I eq .θ& 2 = .I .θ& 2 + .M .(θ&.R) 2
2
2
2
1
1
1
.M eq .V 2 = .M .V 2 + .I .(V / R) 2
2
2
2
I
M eq = M + 2
R
33
Dönme ve Öteleme Hareketi Yapan Sistemlerin İndirgenmesi :
34
Dişli Sistemlerin Atalet İndirgmesi :
N 1 D1 W 2
=
=
N 2 D2 W 1
Dönme Eşdeğeri :
1
1
1
.I eq .θ& 2 = .I .θ& 2 + .M .(θ&.R) 2
2
2
2
2
I eq = I + M .R
θ&eq = θ&, V = θ&.R
35
36
Dişli Sistemlerin Atalet İndirgmesi :
Dişli Sistemlerin Atalet İndirgmesi :
N1 D1 W 2
=
=
N 2 D2 W 1
N 2 D2 W 1
=
=
N 1 D1 W 2
1
1
1
E eq = .Ieq .θ& eq 2 = .I1 .θ& 12 + .I2 .θ& 2 2
2
2
2
θ& eq = θ& 1
N
θ& 2 = θ& 1 . 1
N2
θ& eq = θ& 1
D
θ& 2 = θ& 1 . 1
D2
Ieq = I1 + I2 .( N1 / N 2 )2
SORU! İndirgeme I2 ‘nin şaftına yapılırsa eşdeğer atalet ne olur?
37
38
Yay Sistemlerinde İndirgeme:
Yay Sistemlerinde İndirgeme:
Eşdeğer torsiyon yay sabitinin bulunması :
Eşdeğer torsiyon yay sabitinin bulunması :
T
F
K t = s , K = s , Ts = Fs .L
θ
x
39
40
Yay Sistemlerinde İndirgeme:
Yay Sistemlerinde İndirgeme:
Eşdeğer torsiyon yay sabitinin bulunması :
T
F
K t = s , K = s , Ts = Fs .L
θ
x
x
θ = , x << L
L
Fs . L Fs 2
Kt =
=
. L = K . L2
x/ L
x
Eşdeğer torsiyon yay sabitinin bulunması :
T
F
K t = s , K = s , Ts = Fs .L
θ
x
x
θ = , x << L
L
Fs . L Fs 2
Kt =
=
. L = K . L2
x/ L
x
Bir yayda depolanan potansiyel enerji :
Ep =
x max
x max
x=0
0
∫ F . dx = ∫ K. x. dx = (1 / 2). K. x
θ max
Ep =
41
2
θ max
∫ T . dθ = ∫ K .θ . dθ = (1 / 2). K .θ
θ =0
max
s
t
t
2
max
0
42
Yay Sistemlerinde İndirgeme:
Dönme hareketine çalışan yaylar :
Yay Sistemlerinde İndirgeme:
Dönme hareketine çalışan yaylar :
N 2 D2 W 1 θ1
=
=
=
N1 D1 W 2 θ2
N1 D1 W 2 θ2
=
=
=
N 2 D2 W 1 θ1
1
1
1
2
2
2
Eeq = .K eq .θ eq = .K1.θ1 + .K 2 .θ 2
2
2
2
2
2
K .θ + K .θ
K eq = 1 1 2 2 2 ,
θ eq
K eq = K 1 + K 2 .( N1 / N 2 )2
43
Yay Sistemlerinde İndirgeme:
Ötelemeye ve dönmeye çalışan yaylar :
44
Yay Sistemlerinde İndirgeme:
Ötelemeye ve dönmeye çalışan yaylar :
Öteleme Eşdeğeri :
1
1
1
.K eq .x 2 = .K .x 2 + .K t .θ 2
2
2
2
Öteleme Eşdeğeri :
1
1
1
.K eq .x 2 = .K .x 2 + .K t .θ 2
2
2
2
K .x 2 + K t .θ 2
→θ = x / R
K eq =
x2
1
K eq = K + K t . 2
R
45
Yay Sistemlerinde İndirgeme:
Ötelemeye ve dönmeye çalışan yaylar :
46
Damper Sistemlerinde İndirgeme:
Öteleme Eşdeğeri :
1
1
1
.K eq .x 2 = .K .x 2 + .K t .θ 2
2
2
2
K .x 2 + K t .θ 2
→θ = x / R
K eq =
x2
1
K eq = K + K t . 2
R
Dönme Eşdeğeri :
K .x 2 + K t .θ 2
K eq =
x2
K eq = K .R 2 + K t
→ x = θ .R
47
48
Damper Sistemlerinde İndirgeme:
Damper Sistemlerinde İndirgeme:
Damperde yutulan enerji :
Damperde yutulan enerji :
Ed =
vmax
vmax
∫ F .dv = ∫ D.v.dv
d
0
0
Ed =
öteleme hareketi için
vmax
vmax
∫ F .dv = ∫ D.v.dv
d
0
1
2
Ed = .D.vmax
2
0
öteleme hareketi için
1
2
Ed = .D.vmax
2
Ed =
dönme hareketi için
ω max
ω max
∫ T .dω = ∫ D .ω.dω
d
0
t
0
1
2
Ed = .Dt .ωmax
2
49
Yay Sistemlerinde İndirgeme:
Dönme hareketine çalışan damper :
50
Yay Sistemlerinde İndirgeme:
Dönme hareketine çalışan damper :
N 1 D1 W 1 θ1
=
=
=
N 2 D2 W 2 θ 2
N1 D1 W 2 θ2
=
=
=
N 2 D2 W 1 θ1
1
1
1
2
2
2
Eeq = .Deq .weq = .D1.w1 + .D2 .w2
2
2
2
2
2
D .w + D .w
Deq = 1 1 2 2 2 ,
weq
51
Yay Sistemlerinde İndirgeme:
Dönme hareketine çalışan damper :
52
Yay Sistemlerinde İndirgeme:
Ötelemeye ve dönmeye çalışan damperler :
Öteleme Eşdeğeri :
N 1 D1 W 1 θ1
=
=
=
N 2 D2 W 2 θ 2
1
1
1
.Deq .w 2 = .D.v 2 + .Dt .w 2
2
2
2
1
1
1
2
2
2
Eeq = .Deq .weq = .D1.w1 + .D2 .w2
2
2
2
2
2
D .w + D .w
Deq = 1 1 2 2 2 ,
weq
Deq = D1 + D2 .( N1 / N 2 ) 2
53
54
Yay Sistemlerinde İndirgeme:
Ötelemeye ve dönmeye çalışan damperler :
Yay Sistemlerinde İndirgeme:
Ötelemeye ve dönmeye çalışan damperler :
Öteleme Eşdeğeri :
Öteleme Eşdeğeri :
1
1
1
.Deq .w 2 = .D.v 2 + .Dt .w2
2
2
2
D.v 2 + Dt .w2
→ w= v/R
Deq =
v2
1
Deq = D + Dt . 2
R
1
1
1
.Deq .w 2 = .D.v 2 + .Dt .w2
2
2
2
D.v 2 + Dt .w2
→ w= v/R
Deq =
v2
1
Deq = D + Dt . 2
R
Dönme Eşdeğeri :
D.v 2 + K .Dt .w2
→ v = w.R
v2
2
Deq = D.R + Dt
Deq =
55
Yay ve Damperlerin Paralel-Seri Bağlanmaları:
Paralel Bağlanan Yaylar : (iki yay)
K eq = K a + K b
56
Örnek 1 :
Seri Bağlanan Yaylar : (iki yay)
1
1
1
=
+
K eq K a K b
Paralel Bağlanan Damper : (İki damper)
Örnek 2 :
Deq = Da + Db
Seri Bağlanan Damper : (İki damper)
Deq =
Da .Db
Da + Db
57
58