yayılı kuvvetler

İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
YAYILI KUVVETLER
(DISTRIBUTED FORCES)
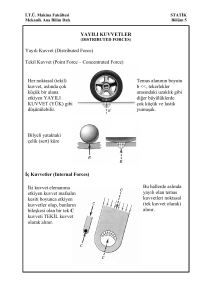
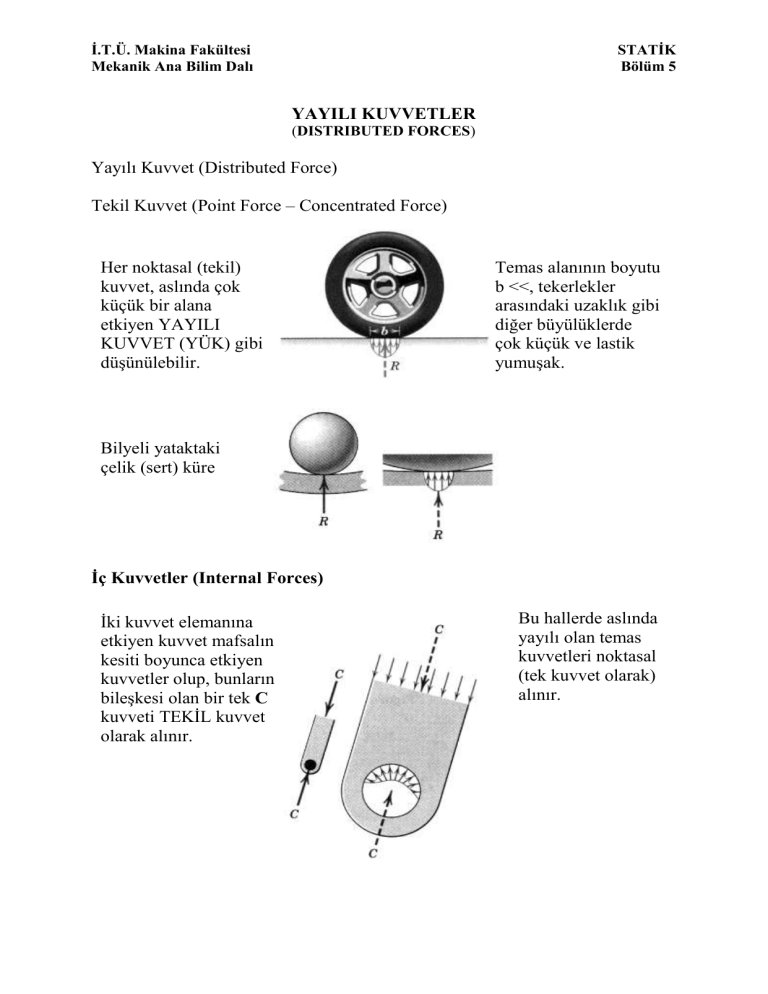
Yayılı Kuvvet (Distributed Force)
Tekil Kuvvet (Point Force – Concentrated Force)
Her noktasal (tekil)
kuvvet, aslında çok
küçük bir alana
etkiyen YAYILI
KUVVET (YÜK) gibi
düşünülebilir.
Temas alanının boyutu
b <<, tekerlekler
arasındaki uzaklık gibi
diğer büyülüklerde
çok küçük ve lastik
yumuşak.
Bilyeli yataktaki
çelik (sert) küre
İç Kuvvetler (Internal Forces)
İki kuvvet elemanına
etkiyen kuvvet mafsalın
kesiti boyunca etkiyen
kuvvetler olup, bunların
bileşkesi olan bir tek C
kuvveti TEKİL kuvvet
olarak alınır.
Bu hallerde aslında
yayılı olan temas
kuvvetleri noktasal
(tek kuvvet olarak)
alınır.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Çizgisel Yayılı Kuvvetler (Line Distributed Forces)
 : yayılı yükün şiddeti
Kuvvetlerin
cisme etkidiği
alanın boyutu
diğer boyutlar
yanında çok
küçük değilse
kuvvetleri yayılı
kuvvetler olarak
alırız.
= birim uzunluğa
etkiyen kuvvet
[ ]=
N
m2
Alana Yayılı Kuvvetler (Area Distributed Forces)
  Birim alana
Baraj kapağına suyun
etkisi (yayılı yük)
etkiyen kuvvet
N
P
m2
 Basınç=Pascal
[ ]=
Kuvvetlerin katı cisim içerisindeki dağılımı STRESS olarak adlandırılır.
Hacme Yayılı Kuvvetler (Volume Distributed Forces)
   g birim ağırlık
Body force (yerçekimi kuvveti)
Birimi :  :
m
 kg   m 
, Sonuç :  3   2 
2
s
 m  s 
N
kg.m
, N: 2
2
m
s
g:
Kütle Merkezi (Mass Center)
T
ip
A
m 1g
G
ip
W
Ser. Cis. Diag.
ip
.. . . m g .. . . .
.. . . . . . .m g m g
m g .
1
n
n
kg
m3
1
A,B, ve C asmalarında
T ile W aynı
doğrultulu olup,
doğrultular bir G
noktasında kesişirler.
G ağırlık merkezidir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Bağlı ve paralel kuvvet sisteminin MERKEZİ:
D1
n
OC 
 F OA
i
D6
i=1
R (Bil.)
F6
F1
i
z
n
F
A1
i
A2
i=1
O
y
O (0, 0, 0)
C (xc, yc, zc)
x
Dn
C (xc, yc, zc)
F2
D2
A5
Fn
u
F5
D
D5
 Fx
F
xc 
i
i
; yc 
i
Fy
F
i
i
; zc 
i
 Fz
F
i i
i
Şeklinde paralel ve bağlı kuvvet sisteminin BİLEŞKESİNİN TATBİK
NOKTASINI (KUVVET SİSTEMİNİN MERKEZİNİ) elde etmiştik.
Bu sonuçları AĞIRLIK VE KÜTLE MERKEZİNİN hesabında kullanacağız.
W OA
W
W x

W
W y

W
W z

W
OG 
i
i
A1
i
xG
z
zG
G
Ai
i i
i
i
y
x
mi
mi g  Wi
m2 A
2
O
i
yG
m1
m1g =w 1
m 2 g =w 2
W  mg
i
W  m1g  m 2 g  ...  m n g
i i
W  (m1  m 2  ...  m n )g
i
W   mi g
W  mg
 mi  m
Bu bağlantılar sürekli cisimler için birer integral ile temsil edilebilirler.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
xG
yG
xdw


 dw
ydw


 dw
STATİK
Bölüm 5

 dw  toplam ağırlık 

 Ağırlık Merkezi
zdw


, zG 

dw


G cismin ağırlık merkezidir.
Dw = gdm ; w = (m1 + m2 +…+ mn)g = mg alınarak,
xG
yG
zG
xgdm  xgdm  xdm 





m 
 gdm gm

 ygdm   ygdm   ydm 

m 
 gdm gm

zgdm
zgdm
zdm





gm
m
gdm


Kütle Merkezi
xG  x , yG  y , zG  z alınabilir.
Sürekli ve Homojen cisimlerde Kütle Merkezi ile Ağırlık merkezi çakışıktır.
dm =  dV ;  : yoğunluk, dV hacim elemanı konulursa, G kütle merkezinin
ifadesi ;
 x dV
  dV
x  xG 
y  yG
 y  dV

  dV
z  zG 
 z  dV
  dV
şeklini alır.
x  xG
 ve eğer
   sb

ise




y  yG
z  zG
xdV  xdV 




V

 dV

ydV  ydV   Geometrik Merkez 





Centroid  Sentroid 
V

dV



zdV
zdV

 


V 
 dV

İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Eksenlere göre Varignon Teoremi uygulanırsa;
Ağırlık
merkezi
bulunur. dW = g.dm ve W = m.g yazılırsa;
Kütle
merkezi
bulunur.
Yukarıdaki skaler bağıntılar vektörel formda yazılabilir. Bunun için;
r  x i  yj  z k
r  xi  yj  zk
olduğu düşünülerek;
Kütle merkezinin
yer vektörü
bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
dm = dV ve m = V yazılırsa;
bulunur.
Çizgisel Elemanların Kütle Merkezi :
xG  x 
x
 xdm
 dm
 x(  AdL)
  AdL
ρ ve A kesiti sabit ise
Yukarıdaki çizgisel eleman için,
yerleştirilirse;
yukarıdaki formüllerde
dm=AdL
Sentroid
bulunur.
Yüzeysel Cisimlerin Kütle Merkezi :
Yukarıdaki formüllerde dm = .t.dA yerleştirilirse (t yüzeyin kalınlığı);
t ve  sabit ise
ρ ve t sabit değilse
 xtdA
x
  tdA
 y tdA
;y
 tdA
z  tdA 

;z 


tdA


Kütle Merkezi olur.
   ( x, y, z ) ve t  t ( x, y, z ) olabilir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Hacimlerin Kütle Merkezi :
x 
 xdm
 dm
;y 
 ydm
 dm
;z 
 zdm
 dm
Yukarıdaki formüllerde dm = .dV yerleştirilirse;
x
 x dV
  dV
ve   sb. ise
bulunur.
Integrasyon Elemanının Seçimi : 1) Elemanın mertebesinin seçimi
Alan elemanı dA = l.dy seçilebilir. dA = dx.dy şeklinde seçilmemelidir.
Hacim elemanı dV = r2.dy seçilebilir. dV = dx.dy.dz şeklinde seçilmemelidir.
2) Elemanı seçerken, integrasyon boyunca sürekliliğe dikkat etmek gerekir.
Bir tek sürekli işlem ile bölgede integral alınabilmeli.
y
.
.
.
.......
... ..
. ..
. .... .
.. .. .
... Seçilmeli dy
... . için tek işlem
. ..
x1
x
Seçilmemeli
x=x1 de
yükseklikte
süreksizlik
var.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
3) Yüksek mertebeden küçük terimler ihmal edilebilir.
dA=ydx
dxdy
 1
2
dx  1
in yanında
ds 
dsdy
2
ihmal edilir
dy  1
ds=
Limit halde hata yoktur.
ihmal edilebilir.
4) Verilen alanın sınırlarını en iyi temsil eden eksen takımı seçilir.
x, y dik
eksen
takımı
uygun
r,  polar
koordinat
uygun.
5) Alan veya hacim elemanı seçildiğinde, değişken koordinatın, elemanın kütle
merkezi olduğuna dikkat etmek gerekir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Bileşik Cisimlerin Kütle Merkezi :
Kütle merkezinin konumunun bulunması istenen cisim karmaşık bir geometriye
sahip ise ve cisim, geometrik merkezi kolayca bulunabilen birçok parçaya
ayrılabiliyorsa, karmaşık geometrili (bileşik cisim) cismin kütle merkezinin
koordinatları, diğer basit cisimlerin kütle merkezlerinin koordinatlarından
yararlanılarak bulunabilir.
 m OG
OG 
m
i
i
m1OG 1  ...  mn OG n
m1  m2  ...  mn
i i
i
i

m x
m
m y

m
m z

m
xG 
yG
i
i
i
zG
i i
i
Varignon teoremi kullanılarak,
ve
bulunur. NOT: m yerine L, A veya V’nin kütlesi alınarak eğrilerin
(uzunlukların), Alanların ve Hacimlerin kütle merkezleri yazılır.
Bazı Kabuller : Karmaşık (bileşik) cisim basit cisimleri kütle merkezi kolay
hesaplanan basit bölümlere ayrılamıyorsa, bu tip cisimlerin kütle merkezinin
koordinatlarının belirlenmesi için bazı kabuller ve yaklaşımlar yapılır.
Örneğin; Karmaşık A alanı aşağıdaki şekilde görüldüğü gibi h.x şeklinde ince
dikdörtgen şeritlere ayrılarak (Bu şeritlerin kütle merkezi xc ve yc ise) kütle
merkezinin koordinatları bulunabilir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Karmaşık bir hacmin kütle merkezinin koordinatları da benzer şekilde x
kalınlığında hacim elemanlarına ayrılarak bulunabilir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
PAPPUS Teoremi
Bir eğrinin veya bir alanın kendisini kesmeyen bir eksen etrafında döndürülmesi
ile elde edilen dönel yüzey veya dönel hacimlerin kütle merkezinin koordinatları
Pappus Teoremi ile kolayca bulunabilir.
Bir Eğrinin x-ekseni etrafında dönmesiyle oluşan üç boyutlu yüzeyin kütle
merkezi için, şekildeki halkanın alanı olan dA = 2ydL ifadesinden yararlanılır.
NOT: y eksen
etrafında dönme
halinde
dA  2πxdL
ydL

y
idi
A  2π  x dL
ve x 
L
 x dL den
 ydL  Ly
L
A=2π x L
konularak
bulunur
Bir A alanının x ekseni etrafında dönmesiyle oluşan hacmin kütle merkezinin
koordinatları da, şekildeki dA alanının dönmesiyle oluşan halka hacmin
integrali ile bulunabilir.
dV = 2ydA
Toplam hacim
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
x etrafında dönme:
dV = 2 ydA
V  2
y
 ydA
 ydA
A
 ydA  yA konulursa
V=2 yA
Varignon teoreminden,
NOT: y ekseni
yA   ydA
etrafında dönme:
dV  2 xdA
yukarıdaki bağıntı kullanılarak, toplam hacim;
V  2π  xdA
x
 xdA dan
A
V  2πxA
şeklinde yazılabilir.
Eğer dönme açısı 2 den daha küçük bir  açısı kadar ise, bu durumda,
yukarıdaki bağıntılardan da yararlanarak, dönel yüzeyin A alanı ve dönel
hacmin V değeri,
NOT: y ekseni
etrafında dönme
halinde:
A   xL
ve
V   xA
şeklinde bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Problem: Verilen paralel ve bağlı kuvvet sisteminin bileşkesini, O
noktasına göre momentini ve bileşkenin oxy düzlemini kestiği (Sistemin
merkezini) noktayı belirleyiniz.
z
R  (75  30  120)k  (80  150)k
R, 95N
R  95k N
80 N
75N O
120N
M 0  4i  75k  (6i  2 j)  30k
y (2i  2 j)  ( 80k )
50N
30N
2m
2m
(4i  4 j)  (50k )  (2i  6 j)  (120k )
M 0  420i  360 j
2m
2m
x
2m
2m
R.M0 = İnvaryant  0 bulunur. Sistem bir tek kayan vektöre indirgenebilir. Bu
bir tek kayan vektör r = R olup tesir çizgisi sistemin eksenidir.
OC 
 F OA
F
i
i

i
xC 
F1 x1 +F2 x2 +...+Fn xn 75(4)  30(6)  80(2)  50(4)  120(2)

F1 +F2 +...+Fn
95
360
 3, 79m
95
F y  F2 y2  ...  Fn yn 75(0)  30(2)  80(2)  50(4)  120(6)
yC  1 1

F1 +F2 +...+Fn
95
xC 
yC  4, 42m
veya:
M 0  r  R  OC  R
420i -360j = (xC i +yC j)  95k
420
 4, 42m
i : 420  95 yC 
95
aynı sonuç.
 
j :  360  95 xC 
360
xC 
 3, 79m
95
yC 
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Problem: Şekildeki taralı alanın ağırlık merkezini belirleyiniz.
n
OC 
 FiOAi
6m
i=1
7,5m
n
F
II
i
III
I
i=1
7,5m
xC 
gm1 x1  gm2 x2  gm3 x3
gm1  gm2  gm3
xC 
m1 x1  m2 x2  m3 x3  s1 x1   s2 x2   s3 x3 s1 x1  s2 x2  s3 x3


m1  m2  m3
 s1   s2   s3
s1  s2  s3
Eleman
I
Üçgen
Alan
xCi
Si
(18)(15)/2 2h/3 =
= 135
2(18)/3 = 12
21x15
II
Dikdörtgen = 315
III
Daire
.r2 = .9
=28,26
Top
421,74
18m
yCi
13m
xCi Si
yCi Si
h/3=15/3 135x12
=5
=1620
135x5
=675
18 + 21/2
=28,5
h/2 = 7,5 315x28,5
= 8977,5
315x7,5
=2362,5
18+13=31
7,5
28,26x31
=876,06
28,26x7,5
=212
9721,44
2825,5
1620  8977,5  876, 06 9721, 44

 23, 05m
135  315  28, 26
421, 74
675  2362,5  212 2825,5
yC 

 6, 7m
421, 74
421, 7
xC 
8m
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Problem : Yoğunluğu bir ucundan uzaklığının  katı olan L
uzunluğundaki doğrusal ince bir telin kütle merkezini bulunuz.
 x ekseni simetri 
y C  0, 

 ekseni seçildi 
xC 
y
 xdm   x dL
 dm  dL
A
L
O
L
x3 L
 |
2
0
xC  L
 32 L0  L
x
3

|

x
dx
0
2 0
 x( .x)dx
x
dx
dm   dL
  x dx
2
C( L, 0)
3
dL
Örnek Problem:
2 merkez açılı r yarıçaplı çember yayının (düzgün) kütle merkezini bulunuz.
x C simetri eskeni
y
d
seçildi  yC  0
3dL=rd
 xdm   x rd
 dm   rd
 xrd   r cos  d

 rd
 rd
xC 
 
x

2
xC
dm   dL
+α
2
r
xC 
r
sin  |
-α
+α
 |

r sin 
dm   rd

x  r cos 
-α
NOT:  =

2
ise x C 
 = ise x C 
C(0,0)
r sin 

r sin


2  2r yarım çember

2
 0 çember
r
x
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Problem: Merkez açısı 2 olan daire parçasının kütle merkezini
bulunuz.
x simetri ekseni seçildi
d
yC  0
xC 
 xdm   x rdrd
 dm   rdrd
dr

O

x

3dL=rd
x
r +α
xC 
  2cos d dr
0 -α
r
xC 
rd
  rd dr
r
+α
2
 r sin  | dr
-α
0
r
+α
 2sin .r dr
2

0
r
  | dr
 2 dr
0
0
-α
dA  rd dr
dm   rd dr
x  r cos 
3 r
r
|
sin 3 0 2r sin 
xC 

 r2 r 3 
|
20
NOT:  =


2
ise ( yarım daire) x C 


2  4r

3
2
4  2r 2 4  4 2 ( Dörtte bir daire)

4
3 2 
3
4
2r sin 
   ise x C 
 0 ( daire)
3 

ise x C 
2r
3
sin
2r
3
sin
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Problem: Şekildeki yarım kürenin kütle merkezini hesaplayınız.
z
z ekseni simetri eksenidir.
. r.
xc ve yc sıfır.
z
zC
a
.O
zdm


dm
z  r dz


  r dz
x
2
zC
2
a
zC 
 z(a
2
2
-z )dz
0
a
2
2
(
a
-z
)dz

0
z2 a z4 a
a
| |
2
4 0  3a
0
zC 
a
z3 a
8
2
a z | |
30
0
3a
C(0,0, )
8
2
dm   ( r 2 )dz
a2  z2  r 2
r 2  a2  z2
dz
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Problem: Şekildeki homojen koninin ağırlık merkezinin koordinatlarını
belirleyiniz.
Z ekseni simetri eksenidir.
z
G (xG=0, yG=0, zG=0)
r
zG 
dw   dV
 zdw
r
dw   ( y 2 dz )
 dw
y
dw   y dz
2
dz
z y dz


  y dz
2
zG

h
2
z
2
zy
 dz
y
 y dz
2
h
3
rz 2
) dz  z dz
z y
h
^0
zG 


h
r2 z2
h
r
2
dz
z
dz
 h2
0
 z(
r3
y
h
z4 h
|
3h
z G  43 h0 
z
4
|
3 0
z
x
O
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek problem. Şekildeki üçgenden dörtte bir daire alanı kesilerek
çıkartılıyor. Geriye kalan alanın geometrik merkezini Pappus –
Guldinus teoremine göre elde ediniz.
Çözüm. Geriye kalan alanı ox ekseni etrafında döndürelim.
Dörtte bir dairenin Ox ekseni etrafında döndürülmesinden
Ortaya çıkan yarım kürenin hacmi
2
y
vK   b3
3
ve üçgenin Ox etrafında
b
döndürülmesinden ortaya çıkan
koninin hacmi
b
1
vKon  (2b)2 (3b)  4b3
3
x
O
b
2b
Taralı alanın Ox etrafında döndürülmesinden ortaya çıkan dönel
cismin hacmi
10b3
v x  v K  v Kon 
3
ekle edilir.
Vx  2yCST olduğuna göre;
=
2
2
12b  b
4
yC 
V
x
2ST

ST = üçgenin alanı -
1
4
dairenin alanı
ifadesi ve Vx değerleri yerlerine yazılırsa
20b
3(12  )
bulunur.Benzer işlemleri Oy ekseni etrafında döndürerek taralı alanın
Oy ekseni etrafında döndürülmesinden ortaya çıkan dönel cismin
hacmi
xC
Vy
2ST

bulunur.
32b
3(12  )
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek problem . Şekilde verilen dörtte bir çember yayının Oy
ekseninin etrafında döndürülmesinden ortaya çıkan dönel yüzeyin
alanını hesaplayınız.
Çözüm . Çember yayının geometrik merkezinin apsisini şekilden
2r
xC  a  r 

2r
şeklinde elde ederiz. Çember yayının uzunluğu L 
dır. Bu
4
değerleri Sy  2Lx C formülünde yerine yazarsak
2r 
2r 
2 a  r   _ 2   bulunur.
a

r



r


 
 
 4 

Sy  2 
y
a
r
xC
O
C
r
x
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Kirişler (Beams) :
Dış kuvvetlerin etkisindeki taşıyıcı sistem olarak kirişler, mühendislik
uygulamalarında çok sık kullanılırlar.
Değişik sınır şarlarında kirişler;
BASİT
ÇIKMA
SÜREKLİ
ÜÇ DESTEKLİ ÇIKMA KİRİŞ
SABİT KİRİŞ
STATİK OLARAK ÇÖZÜLEBİLİR
STATİK OLARAK ÇÖZÜLEMEZ
Yayılı Yükler :
Birim uzunluğa etki eden yayılı yükün büyüklüğüne, o yayılı yükün şiddeti (
veya q) adı verilir.
Yayılı yükün şiddeti sabit, lineer değişen veya bir fonksiyon şeklinde
değişebilir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Şiddeti sabit olan yayılı yük ;
R=L=ALAN
R, Geometrik
merkezden geçer
Şiddeti sıfırdan başlayıp, lineer (doğrusal) değişen yayılı yük ;
= Üçgenin Alanı
R, Sentroidden
(Geometrik
merkez)geçer.
Şiddeti belirli bir değerden başlayıp, lineer (doğrusal) değişen yayılı yük ;
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Şiddeti belirli bir değerden başlayıp, bir fonksiyon şeklinde değişen yayılı yük ;
dx uzunluğuna etki eden kuvvet dR = .dx olduğuna göre, toplam kuvvet,
Yayılı yükün eşdeğeri olan toplam R kuvvetinin uygulama konumu,
şeklinde bulunur.
İç Etkiler
Dış kuvvetlerin etkisindeki bir kiriş, belirli bir konumundan kesildiğinde, kesitte
oluşan etkiler;
- Eksenel Kuvvet (Axial Force)
- Kesme Kuvveti (Shear Force)
- Eğilme Momenti (Bending Moment)
- Burulma Momenti (Torque)
şeklindedir.
:H
:V
:M
:T
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Taşıyıcı sisteme bir dış kuvvet etkidiği zaman sistemde (elemanda) bu dış
kuvveti dengelemeye çalışan bir iç kuvvetler sistemi oluşur.
F1
F3
F1
sol
Kablo Eksen
F2
Fn
F3
sağ
F2
Fn
Dış kuvvetler çekme veya basınç olabilir. Elemanda iç kuvvetler sistemi oluşur.
Elemanın eksenine dik olan bir kesit üzerinde iç kuvvetleri inceleriz. Ortaya
çıkan hayali iki parça da dengede varsayımı yapılır. Birim alana etkiyen iç
kuvvetlerin büyüklüğüne STRESS (Gerilme) denir.
F3
F1
R
F2
Sol serbest cisim diyagramı
M
Fn
Sağ serbest cisim diyagramı
Sol parça
Sol parçadaki iç kuvvetler sistemini kesitin sentroidi olan noktaya taşırsak
Bileşke R ve toplam moment M elde ederiz.
Kesme Kuvveti (Shear Force)
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
Eğilme Momenti (Bending Moment)
Burulma Momenti (Torsion)
Bileşik Etki (Combined Loading)
STATİK
Bölüm 5
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Düzlemsel kuvvetlerin etkisindeki bir kirişte, genellikle, kesme kuvveti ve
eğilme momentinin etkileri önemlidir.
Kesme kuvveti ve Eğilme momentinin işaret notasyonu literatürde, genellikle,
aşağıda görüldüğü gibi seçilir.
Eğilme momentinin etkisi için örnek: Kesiti H-profili olan kirişe pozitif eğilme
momenti etki ederse, alt ve üst flanşlarda şekilde görüldüğü gibi, çekme ve
basınç kuvvetleri oluşur.
Kesit Tesirleri Arasındaki Diferansiyel Bağıntılar:
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Yukarıdaki ifade integre edilerek, Kesme kuvveti ile yayılı kuvvetin şiddeti
arasında bağıntı bulunur.
V = V0 + A
(A : x0 ile x arasında, yayılı yük eğrisinin altındaki alanın negatif değeri)
Şekildeki dx uzunluğundaki elemanın moment dengesi yazılısa;
ve ikinci dereceden küçük terimler ihmal edilerek,
bulunur.
Eğilme momenti ile yayılı kuvvetin şiddeti arasındaki bağıntıyı bulmak için,
yukarıdaki bağıntının türevi alınıp, kesme kuvvetinin  cinsinden ifadesi
yerleştirilirse,
bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Soru:
Şekilde görülen 4KN yükü taşıyan basit kiriş için kesme ve moment dağılımını
belirleyiniz
Çözüm:
Serbest cisim diagramından mesnet tepki kuvvetleri
olarak bulunur.
Öncelikle kirişin başlangıçtan x uzaklığında ve tekil kuvvetin solunda kalan bir
kesit alınır. Üzerinde kesme kuvveti (V) ve momenti (M) pozitif yönlerde
gösterilir ve serbest cisim diagramı çizilir. Denge denklemlerinden aşağıdaki
ifadeler yazılır:
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Bu V ve M değerleri yalnızca kirişin 4 kN`luk tekil kuvvetin solunda kalan
kesitler için uygulanabilir.
İkinci olarak tekil kuvvetin sağ tarafından bir kesit alınır. Dengeden:
sonuçları tekil kuvetin sağ tarafı için bulunur.
Maksimum eğilme momenti kesme kuvvetinin değiştiği yönde ortaya çıktı. V-x
diagramında x=0 dan hareket ettiğimizde an be an taradığımız alan M
momentine eşittir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Soru:
Şekilde ankastre kiriş şiddeti w  wo sin(
x
l
) fonksiyonu ile tanımlı yayılı yüke
maruzdur. Kesme kuvveti ve eğilme momentini
x
oranının fonksiyonları
l
olarak yazınız.
Çözüm:
Ankastre mesnetteki tepki kuvveti ( Vo ) ve momentini ( M o ) hesaplayabilmek
için öncelikle tüm kiriş için serbest cisim diagramı çizilir. Standart olarak Vo ve
M o pozitif yönlerinde gösterilmiştir. Düşey dengeden kesme kuvveti,
şeklinde bulunur. Sol uçtaki (x=0) moment dengesinden M o aşağıdaki gibi
bulunur:
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Başlangıçtan x mesafesindeki keyfi bir kesit için w  
dV
denklemi
dx
kullanılarak kiriş içindeki kesme kuvveti aşağıdaki gibi bulunabilir:
yada boyutsuz formda:
Eğilme momenti ise V 
dM
formülü kullanılarak aşağıdaki gibi bulunur:
dx
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
yada boyutsuz formda:
V
M
ve
nin değişimi şekillerde gösterilmiştir.
wol
wol 2
M
nin negatif değerleri fiziksel eğilme momentinin şekildeki yönün tersi
wol 2
yönde etkidiğini gösterir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Örnek Soru:
Şekildeki gibi yüklenmiş bir kiriş için kesme kuvveti ve eğilme momenti
diagramlarını çiziniz ve oluşacak maksimum momentin sol uçtan mesafesini
hesaplayınız.
Çözüm:
Tüm kiriş için çizilen serbest cisim diagramında yayılı yükler için bileşke tekil
kuvvetler konularak mesnet tepki kuvvetleri rahatlıkla bulunabilir.
Önce ilk aralık (0<x<2) analiz edilir. Düşey denge ve moment eşitliklerinden
aşağıdaki sonuçlar bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
V ve M nin bu değerleri yalnızca (0<x<2) arasında geçerlidir ve diagramlarda
yalnızca bu aralık için çizilmişlerdir.
ikinci aralık (2<x<4) için çizilen serbest cisim diagramı için düşey denge ve
moment dengesi yazılır ise
elde edilir.
Kirişin diğer kısmının incelenmesine üçüncü aralıkta alınan bir kesitin sağ
bölümü için çizilen serbest cisim diagramından devam edilebilir. Şekilde V ve
M nin pozitif doğrultuda gösterildiğini hatırlatalım.
Düşey denge ve moment toplamından aşağıdaki ifadeler elde edilir.
yine bu V ve M değerleri yalnızca ilgili aralıkta (4<x<5) geçerli olduğunu ve
şekilde bu aralık için çizildiğini vurgulayalım.
Son kısımda basit bir gözlem ile analiz gerçekleştirilebilir. Kesme kuvvetinin
her kesitte sabit ve 1.5 kN olduğu görülmektedir. Moment ise kirişin sağ
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
ucunda sıfır olmalı ve verev (çapraz) bir doğru şeklinde bir önceki kısımdaki son
moment değerine kadar azalan x değerleri ile artmalıdır.
Maksimum moment kesme kuvvetinin sıfır eksenini kestiği noktadadır
(x=2.23m). Değeri 2. aralık için bu değerin M ifadesine konulması ile
olarak hesaplanır.
Ayrıca herhangi bir aralık (kısım) için momentin (M) kesme kuvveti
diagramının altındaki alan olduğunu vurgulayalım. Mesela x<2 için bu yolla
moment:
bulunur ki bu yukarıda bulduğumuz ifade ile aynıdır.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Kablo ve Sicimler
Bükülebilen taşıyıcı sistem olarak kablolar ve sicimler, iç etki olarak, sadece
çekme kuvveti taşıyabilirler. Basınç kuvveti, kesme kuvveti, eğilme ve burulma
momentleri taşıyamazlar.
Genel Bağıntılar
Şiddeti değişken bir yayılı yükün etkimesi durumunda, düşey doğrultudaki
bileşke kuvvet,
şeklindedir. Varignon teoremi uygulanarak, bileşke kuvvetin geçtiği konum
bulunabilir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Şekilde c deki elemanın dengesinden,
yazılır. sind =  ve cosd = 1 yazılacak olursa,
İkinci dereceden küçük terimler ihmal edilirse,
veya
bulunur.
Burada 2. bağıntı, T nin yatay bileşeninin sabit olduğunu gösterir. Bu sabit
değeri T0 ile gösterecek olursak ve 1. bağıntıda T = T0 / cos yerleştirirsek,
d (T0 tan  )   .dx
tan  
dy
dx
yerleştirilirse,
bulunur.
Bu ifade, kablonun diferansiyel denklemidir. İntegre edilip, sınır şartları
kullanılarak, kablonun formunu veren y = y(x) fonksiyonu bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Parabolik Kablolar
Kabloya etki eden düşey yayılı kuvvetin şiddeti sabit olsun. Genel olarak,
kablonun iki ucunun aynı yatay doğrultuda bulunmadığını kabul edelim.
Kablo denkleminin integrasyonu ile,
bulunur. Seçilen koordinat sistemi için, x = 0 da eğim, dy/dx = 0 olacağından,
yazılır. Bir kere daha integral alınırsa,
bulunur. Bu ifade düşey parabol denklemidir. Kablo kuvvetinin sabit olan yatay
bileşeni, orijindeki kablo kuvvetidir.
x = lA için y = hA yazılırsa,
bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Şeklin b bölümündeki elemanın dengesinden,
yazılır ve T0 yok edilirse,
bulunur. Maksimum kablo kuvveti x = lA konumundadır ve değeri,
dir.
Kablonun orijin ile A noktası arasındaki uzunluğunun bulunması istenirse,
ds  (dx) 2  (dy) 2
bağıntısı integre edilir.
İntegrasyon için,
seri ifadesi, kullanılırsa,
bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Asma köprülerde kablonun iki ucu genellikle aynı yatay konumdadır. Bu
durumda kablonun iki ucu arasındaki mesafe L = 2 lA ve toplam kablo uzunluğu
S = 2 sA dır.
Bu değerler kullanılarak, maksimum kablo kuvveti ve toplam kablo uzunluğu,
şeklinde bulunur.
Zincir Eğrisi
Kabloya etki eden dış kuvvetin sadece üniform olan kablo ağırlığı olduğunu
düşünelim. Bu durumda, şekildeki elemanın serbest cisim diyagramı
değişecektir.
Kablonun birim uzunluğunun ağırlığı  ise, bileşke kuvvet R = .s dir. .dx
kuvveti ise, .ds değerine eşit olacaktır.
Bu durumda kablo diferansiyel denklemi,
formundadır.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
(ds)2 = (dx)2 + (dy)2
bağıntısı kullanılarak,
dy/dx = p yazılacak olursa, diferansiyel denklem,
şeklini alır ve integrasyon sonucunda,
yazılır. X = 0 konumunda dy/dx = p = 0 olduğundan C = 0 dır. dy/dx = p
yazılırsa,
bulunur. Tekrar integre edilirse,
bulunur. K integral sabiti, x = 0 da y = 0 yazılarak hesaplanır.
Bu durumda,
K = - T0 / 
yazılarak,
bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Bu bağıntı iki ucundan asılan, kendi ağırlığının etkisindeki kablonun aldığı
formdur ve Zincir Eğrisi olarak bilinir.
Şekildeki elemanın serbest cisim diyagramından,
dy
 tan   s / T0
dx
bağıntısı kullanılarak, kablo uzunluğu,
şeklinde bulunur. Şekildeki elemanın kuvvet dengesinden,
veya
veya
veya
bulunur.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
TEKİL YÜKLÜ KABLOLAR
y
AB=a=Kablo Açıklığı
H=çökme
By
Ay
Bx
1
L1
y1
2
x1
L2
F1
4
y3
h  y2
L3
L4
4
3
x2
F3
F2
Not: Diğer taşıma sistemlerinde
olduğu gibi tüm sistemin serbest
cisim diagramından  Fx  0 ,
 Fy  0 ve  M  0 yazılır. Ax, Ay,Bx , By çözülmeye çalışılır. Ancak üç
denklem ve dört bilinmeyen olduğundan sistem çözülemez. Kablonun çeşitli
kesimlerinin serbest cisim diagramları çizilerek denklem sayısı artırılır.
x3
By
Ay
Ax
T1
4
1
T1
T4
2
T2
T2
3
F3
F1
F2
T4
4
T3
T3
Bx
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Tüm sistem için:
 M A = 0  aBy  F1x1  F2 x2  F3 x3  0
1
By  ( F1 x1  F2 x2  F3 x3 ) bulunur.
a
1
 Fx  0  Ay  By  F1  F2  F3  0  Ay F1  F2  F3  a (F1x1  F2 x2  F3 x3 )
bulunur.
A noktasında:
 Fx  0   Ax  T1 cos1  0
 Ax  T1 cos1 bulunur.
F1`in etkidiği noktada:
 Fx  0  T1 cos1  T2 cos2  0 yazılır.
Ax  T1 cos1  T2 cos 2  ......  T4 cos 4  Bx elde edilir.
SONUÇ
*Kablo kuvvetininyatay bileşeni sabit olup mesnet noktalarındaki bağ
kuvvetinin yatay bileşenine eşittir.
*θ büyüdükçe cos θ küçüleceği için maksimum kablo kuvveti θ`nın en
büyükolduğu mesnet civarında çıkar.
Ax  T1 cos1 , Ay  T1 sin 1 ve Bx  T4 cos 4 , By = T4 sin 4
T1  Ax 2  Ay 2 , T2  Bx 2  By 2
Bunlar en büyük kablo kuvvetleridir.
A
A
B
tan 1 y  1  tan 1 y ve  4  tan 1 y
Ax
Ax
Bx
Not: Eğer maksimum T veya θ biliniyor ise bu son denklemden mesnetlerdeki
Ax=By elde edilir.
Not: Ax ve Bx bilindikten sonra T1, T2,T3,T4,y1,y2,y3 büyüklükleri (b)serbest ciim
diagramından elde edilir.
Not: kablonun herhangi bir noktsının koordinatlarının bilinmesi halinde mesnet
kuvvetlerinin yatay bileşenlerini bulabiliriz. Örneğin kabloyu herhangi bir D
noktasında kesip srbest cisim diagramını çizersek:
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
 M D  0  Ay xD  F1( xD  x1)
y
 F2 ( xD  x1 )  Ax yD  0
1
Ax 
 [ Ay xD  F1 ( xD  x1 )  F2 ( xD  x1 )]
yD
 Bx elde edilir.
Ay
Ax
x
y1
y2
yD
T3
x1
D
F1
x2
F2
xD
Not: kablo uzamaz olduğundan L=toplam uzunluk= L1+L2+L3
L  x12  y12  ( x2  x1)2  ( y2  y1)2  ( x3  x2 )2  ( y3  y2 )2  (a  x3 )2  y32
Bulunur. El ile çözüm çok emek ister. Bilgisayar tercih edilir.
Örnek Problem: Maksimum 1000N kablo kuvvveti olan bir kabloda 1) Ax, Ay,
Dx, Dy bağ kuvvetlerini 2) T1, T2 ,T3 kablo kuvvetlerini 3) yB, yC düşey
uzunluklarını (çökmelerini) 4) Kablonun L uzunluğunu bulunuz.
Çözüm:
A
10
12
12
yB
D
yC
C
B
200N
500N
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
1)Tüm Sistem:
Dy
Ay
Ax
1
A
Dx
3
D
3
1
B
2
C
200N
MD  0
 Ay *34  500*22  200*10  0
Ay  382 N
500N
Maksimum çökme B de ve maksimum kablo kuvveti θ1 açısında ortaya çıkar.
Tmaks  Ax 2  Ay 2  Ax  Tmaks 2  Ay 2  10002  3822
Ay
Ay  924 N
A
382
tan 1  y  1  tan 1
 22.280
Ax
924
A
Ax
1
Tekrar tüm sisteme dönersek:
 Fx  0   Ax  Dx  0  Ax  Dx  924 N
 Fy  0  Dy  500  200  Ay  0  Dy  700  Ay
 Dy  318 N
2) B ve C nin serbest cisim diagramlarından
T1
1
T2
2
500N
 Fx  0  T2 x  T1x  0  T2 cos2  T1 cos1  0
T2 x  T2 cos2  T1 cos1  1000*cos 22.480
T2 x  924 N
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
 Fy  0  T2 y  T1y  500  0  T2 sin 2  T1 sin 1  500  0
T2 y  T2 sin  2  T1 sin 1  500  1000sin 22.480  500
T2 y  117.6 N
2  tan 1 
T2 y
117.6
 tan 1
 7.2560
T1 y
924
T2  T2 x 2  T2 y 2  9242  117.62  931.4 N
C Noktası :
T3
2
T2
3
200N
 Fx  0  T3x  T2 x  0 
T3 x  T2 x  T2 cos 2  931.4 cos 7.256
T3 x  T2 x  923.7 N
 Fy  0  T3 sin 3  T2 sin 2  200  0
T3 y  T3 sin 3  200  T2 sin 2  200  931.4sin 7.2560
 317.6 N
T3  T3 x 2  T3 y 2  977 N Not: D noktasını kontrol için kullanabiliriz
3  tan 1
3)
T3 y
 18.9740
T3 x
yB  12 tan 1  12 tan122.480  4.97cm
yC  10 tan 3  10 tan18.9740  3.44cm
2
2
2
2
2
2
4) L  L1  L2  L3  12  4.966  12  (4.966  3.439)  10  3.439
L  35.7cm
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
UYGULAMA
Problem 5/141
Şekilde görüldüğü gibi, yatayda üniform (şiddeti sabit) yayılı yük taşıyan
kabloda T0 kablo kuvvetini bulunuz. Kablonun B mesnetinde yatayla yaptığı
açıyı hesaplayınız.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Problem 5/143
Kütlesi ihmal edilebilen kablo şekilde görüldüğü gibi iki noktadan tespit
edilmiştir. Kablonun bağlandığı alt mesnette kablo teğeti yatay olacak kadar bir
kablo kuvveti oluşmuştur. Kabo şiddeti x=0 da 1000 N/m den başlayarak, x2 ile
orantılı olarak azalmaktadır. Kablonun aldığı formu, y = y(x), bulunuz.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Problem 5/150
A ve B noktalarından şekildeki gibi tespit edilmiş olan kablonun uzunluğunu
hesaplayınız.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Akışkanların Statiği
Bu bölümde, akışkan basıncından kaynaklanan kuvvetlerin etkisindeki
cisimlerin dengesi incelenecektir.
Akışkan Basıncı
Pascal kanununa göre, akışkan içinde herhangi bir noktadaki basınç her
doğrultuda aynı değerdedir. Bu, aşağıdaki elemanın dengesinden kanıtlanabilir.
Elemanın yüzlerine etki eden basınç p1, p2, p3, ve p4 olsun. Bu durumda,
ds.sin = dy ve ds.cos = dx olduğuna göre,
bulunur.
Elemanın 90 derece döndürülmesi durumunda, diğer yüze etki eden basıncın da
eşit olduğu görülür.
dh kalınlığındaki elemanın kuvvet dengesinden,
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Yukarıdaki ifadenin integrasyonundan,
bulunur. Burada p0 değeri, h = 0 daki akışkan yüzeyinin basıncıdır (atmosfer
basıncı).
Basınç ölçüm cihazları, atmosfer basıncından değişimi ölçtüğü için, h
derinliğindeki ölçüm basıncı,
p = gh
olacaktır.
Basınç için en fazla kullanılan SI birimi kilopascal (kPa) dır.
Su İçine Daldırılmış Dikdörtgen Levha
Su içine daldırılmış dikdörtgen levha düşey ile  açısı yapsın ve su yüzeyi x –y’
düzlemi olsun.
2 noktasına etki eden basınç, .g ile 2 noktasının su yüzeyinden derinliğinin
çarpımına eşittir (6-2 vektörü). b kenarı boyunca (su yüzeyine paralel 2-3
doğrultusu) bütün noktalardaki basınç aynıdır. Benzer şekilde, 1-4
doğrultusundaki noktalardaki basınçlar aynı ve .g ile 1 noktasının su
yüzeyinden derinliğinin çarpımına eşittir (5-1 vektörü).
Dikdörtgen üzerine etki eden basıncın oluşturduğu bileşke kuvvet R dir ve
basınç merkezi denen bir noktaya etki eder.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
1-2 kenarı boyunca basınç değişimi trapezoid şeklindedir.
Levhanın üst kenarına paralel, dy kalınlığındaki bir alan elemanına etki eden
kuvvet,
dR = p.dA = p.b.dy
Ancak p.dy şekildeki dA’ alanına eşittir. Dolayısıyla yüzeye etki eden
bileşke kuvvet,
Buradaki A’ alanı, levha kenarı boyunca basınç değişimini tanımlayan
trapezoidin alanıdır.
Port. = (p1 + p2) / 2 olduğu düşünülürse,
Burada,
h  y.cos
dir.
R bileşke kuvvetinin etki ettiği konumu belirlemek için, akışkan yüzeyindeki B
noktasına göre moment alarak Varignon teoremi uygulanırsa,
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
bulunur.
Silindirik Yüzeylere Etki Eden Hidrostatik Basınç
Sıvı içine daldırılmış eğrisel yüzeylere etki eden basınç kuvvetlerinin hesabı
düzlem levhalara etki eden kuvvetlerin hesabından daha değişik ve zordur.
Şekilde böyle bir eğrisel yüzey elemanı görülmektedir. Elemanın düşey kesitleri
hep AB eğrisi formundadır ve aynı basınç değişiminin etkisindedir. Düşey kesit
aşağıdaki şekilde görülmektedir.
R bileşke kuvvetinin doğrultusu devamlı değişeceğinden, x ve y bileşenlerinin
integrasyonu uygun olacaktır.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
R nin etki ettiği konum için moment denge denklemi gerekecektir.
R nin bulunması için daha basit bir başka yol, yüzey üzerindeki ABC su
blokunun dengesinin incelenmesidir.
Herhangi bir Geometrideki Yüzeye Etki Eden Hidrostatik Basınç
Cismin yüzeyi düşey ile  açısı yapsın. Şekilden, dR = p.dA = g.dA
olacağında, bileşke kuvvet
şeklindedir.
h A   hdA
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
bağıntısı kullanılarak,
bulunur.
R bileşke kuvveti, ayrıca şekildeki V’ hacmi ile de tanımlanabilir.
Varignon teoremi kullanılarak,
yazılır. Bu değer, R bileşke kuvvetinin geçtiği konumu tanımlar.
Kaldırma Kuvveti (Buoyancy)
Archimedes Prensibine göre, bir akışkan içine daldırılmış bir cisme, cismin
hacmi kadar akışkan ağırlığına eşit bir kaldırma kuvveti (buoyancy) etki eder.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
Kaldırma kuvvetinin sonucu olarak, önemli bir nokta, akışkan içine daldırılmış
olan cismin stabilitesidir.
Aşağıdaki su içinde bulunan gemide, B noktası geminin akışkan içindeki
bölümünün kütle merkezi (kaldırma merkezi), G ise cismin bütününün kütle
merkezidir.
Kaldırma kuvveti F, B kaldırma merkezinden geçer, cismin W ağırlığına eşit ve
zıt yöndedir.
Geminin bir  açısı kadar yan yatması durumunda, geminin batan kısmının
hacmi değişecektir ve kaldırma merkezi B’ gibi bir nokta olacaktır.
B’ den geçen düşey doğrultunun, geminin merkez eksenini kestiği M noktasına
Metasenter (metacenter) adı verilir. M ile G arasındaki mesafe metasentric
yükseklik olarak adlandırılır.
M noktası G nin üstünde ise, şekilden de görüleceği gibi oluşan kuvvet çifti,
gemiyi düzeltecek yöndedir.
M noktası G nin altında ise, oluşan kuvvet çifti gemiyi daha fazla yana yatıracak
yöndedir ve geminin stabilitesi bozulmuş demektir.
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5
UYGULAMA PROBLEMLERİ
İ.T.Ü. Makina Fakültesi
Mekanik Ana Bilim Dalı
STATİK
Bölüm 5