Document

Bazı Kesikli Olasılık Dağılımları
Hatırlatma: ( U  P ) bir olasılık uzayı ve
X 

R


X ( )
olmak üzere,  a  R için,
{    X ( )  a}  U
oluyorsa X fonksiyonuna bir Rasgele Değişken denir.
DX = X ()  {x : x  R ,    için X ( )  x}
olmak üzere, DX kümesi sonlu veya sayılabilir sonsuz elemanlı olduğunda X e kesikli rasgele
değişken (discrete random variable) denir. Bu ders döneminde kesikli dağılımlardan sırasıyla
Bernoulli, Binom, Hipergeometrik, Geometrik, Negatif Binom (Pascal), Poisson ve Düzgün Dağılımı
göreceğiz.
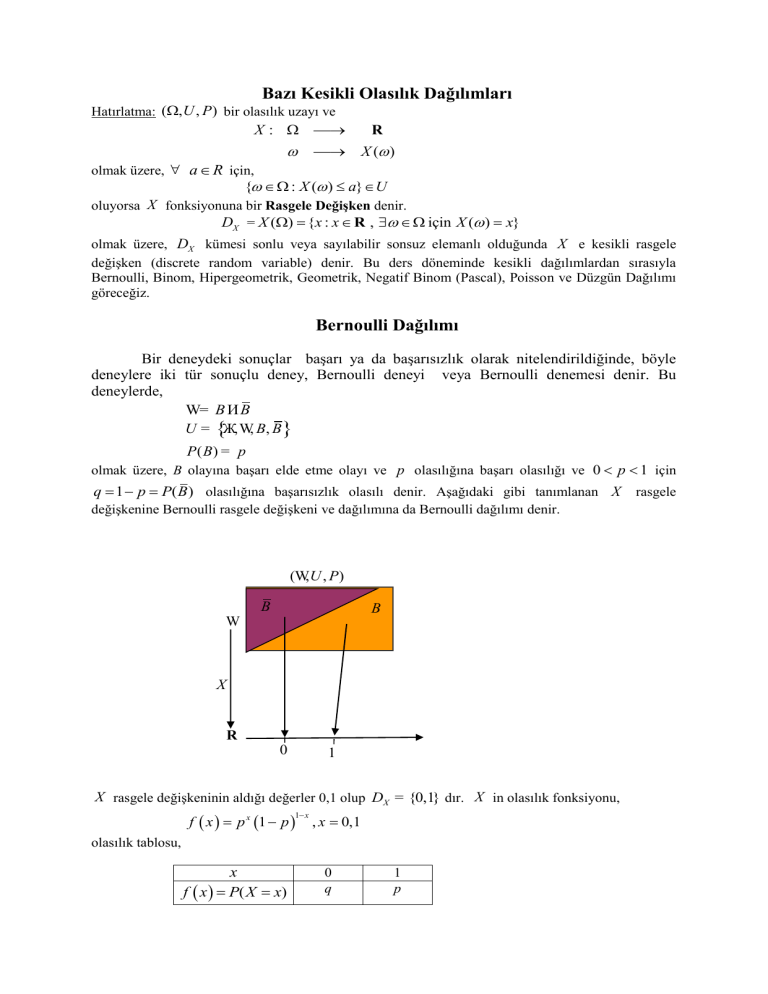
Bernoulli Dağılımı
Bir deneydeki sonuçlar başarı ya da başarısızlık olarak nitelendirildiğinde, böyle
deneylere iki tür sonuçlu deney, Bernoulli deneyi veya Bernoulli denemesi denir. Bu
deneylerde,
W= B И B
U = {Ж, W, B, B }
P( B) = p
olmak üzere, B olayına başarı elde etme olayı ve p olasılığına başarı olasılığı ve 0  p  1 için
q  1  p  P( B ) olasılığına başarısızlık olasılı denir. Aşağıdaki gibi tanımlanan X
değişkenine Bernoulli rasgele değişkeni ve dağılımına da Bernoulli dağılımı denir.
(W,U , P)
B
B
w
W
X
R
0
1
X rasgele değişkeninin aldığı değerler 0,1 olup DX = {0,1} dır. X in olasılık fonksiyonu,
f  x   p x 1  p 
1 x
, x  0,1
olasılık tablosu,
x
f  x   P( X  x )
0
q
1
p
rasgele
dağılım fonksiyonu,
x0
0 ,

F  x   q , 0  x  1
1 ,
x 1

ve
E  X    x. f  x   0.q  1. p  p
E  X 2    x 2 . f  x   02.q  12. p
Var  X   E  X 2   E  X   p  p2  p 1  p   p.q
2
M X  t   E  etX    etx f  x   et .0 .q  et .1. p  q  p.et  1  p  p.et
x
dır. Bernoulli dağılımında, beklenen değer başarı elde etme olasılığına eşittir.
Bernoulli dağılımındaki p ( 0  p  1 ) sayısına dağılımın parametresi denir. Bernoulli
dağılımları arasında varyansı en büyük olan dağılım hangisidir ? Bernoulli Dağılımının
varyansı p ’nin bir fonksiyonudur.
g ( p) = pq = p(1- p) = p - p 2 , 0 < p < 1
g '( p ) = 1- 2 p
g ''( p ) = - 2
1
olmak üzere, p = olan Bernoulli dağılımının varyansı en büyüktür. Parametresi ½ olan
2
Bernoulli dağılımı en büyük varyanslıdır.
Bernoulli dağılımını iki tür sonuçlu deneylerinin modellenmesinde (anlatımında)
kullanırız. Örneğin 200 kişilik bir kitlede 120 kişi sigara içmiyor ve 80 kişi içiyor, yani %60’ı
sigara içmiyor olsun. Bu kitleden rasgele bir kişi seçildiğinde Örnek Uzay,
W= {sigara içiyor, sigara içmiyor}
olmak üzere, seçilen kişinin sigara içmiyor olması olayının olasılığı p=0.6 olup, X rasgele
değişkeni sigara içmeyen için 1, içen için 0 değerini alsın. X bir Bernoulli rasgele değişkenidir.
p
Bir olayın olasılığı p olmak üzere,
sayısına, bu olayın değiline göre karşıtlığı diyelim.
1- p
p
Kısaca
sayısına karşıtlık (odds) diyelim. (Odds: the ratio of the probability of one event to
1- p
that of an alternative event.) Karşıtlık (0, Ґ ) aralığında bir sayıdır. Yukarıda sözü edilen kitlede,
0.60
120
= 1.5 =
= 120 : 80 = 3 : 2 dır. Sigara içmeyen 3
sigara içmemenin içmeye karşıtlığı
1- 0.60
80
kişiye karşılık 2 kişi sigara içmektedir. Ölümcül bir tür kanser tedavisinde %80 olasılıkla başarı elde
ediliyorsa,
Karşıtlık =
0.80
= 4 :1
1- 0.80
dır.
Bir olay için karşıtlık
olay için
p1
p2
ve başka bir olay için karşıtlık
olmak üzere, bu iki
1 - p1
1 - p2
p1
1- p1
p (1- p2 )
Karşıtlık Oranı (Odds Ratio, OR) =
= 1
p2
p2 (1- p1 )
1- p2
olarak tanımlanmaktadır. Ölümcül bir tür kanser tedavisinde başarı olasılığı, bayanlar için p1 =%80,
erkekler için p2 =%40 olduğunda, bir bayanın kurtulma olasılığı erkeğin iki katıdır. Bayanlar için
Karşıtlık B =
p1
0.80
4
=
= = 4
1- p1 1- 0.80 1
olmak üzere, 4 kurtulan bayana karşılık 1 bayan ölmektedir. Erkekler için,
Karşıtlık E =
p2
0.40
4 2
=
= =
1- p2 1- 0.40 6 3
olup, 4 kurtulan erkeğe karşılık 6 erkek ölmektedir. Bu karşıtlıkların oranı,
p1
0.80
4
1- p1 1- 0.80 1
OR =
=
= = 6
p2
0.40
4
1- p2 1- 0.40 6
dır. Tedavi sonrası bir bayanın kurtulma olasılığı erkeğin kurtulma olasılığının iki katı, Karşıtlık Oranı
ise OR=6 dır.
Bir tedavide başarı oranı (olasılığı), sigara içme oranı, bozuk ürünlerin oranı, 80 yaşın
üzerindekilerin oranı, kısaca bir kitlede belli bir özelliğe sahip nesnelerin oranı kitleyi karakterize
etmede önemli parametrelerden birisidir. Ayrıca bu parametreye bağlı olarak Karşıtlık ve Karşıtlık
Oranı gibi kavramlar söz konusudur. Bir kitlede belli bir özelliğe sahip nesnelerin oranı, bir Bernoulli
denemesinde başarı olasılığı p ( 0  p  1 ) olmak üzere, p parametresi bilinmediğinde tahmin edilmesi
gerekmaktadir. Bernoulli Dağılımının p parametresinin tahmin edilmesi problemini bu dersin sonunda
ve önümüzdeki derste ele alacağız.
Binom Dağılımı
Başarı olasılığı p olan bir Bernoulli denemesinin aynı şartlar altında, bağımsız olarak n kez
tekrarlanmasıyla oluşan deneye Binom Deneyi denir.
1. Tura gelmesi başarı sayılan bir para atışının 10 kez tekrarlanması,
2. Kusursuz parça üretme olasılığı p  0.99 olan bir makinada 10 tane parça üretilmasi,
3. Bir atışta başarı olasılığı p  0.80 olan bir basketbolcunun 5 atış yapması,
4. 6 Kırmızı ve 4 siyah top içeren bir kavanozdan iadeli olarak 3 top çekilmesi,
birer Binom Deneyidir.
Binom Deneyinde örnek uzay,
м
ь
п
п
п
W= п
BB
...
B
,
BB
...
B
,
BBB
...
B
,...,
BB
...
B
,
BB
...
B
,...
BB
...
BBB
,
BBBB
...
B
,...,
BB
...
BBBB
,...,
BB
...
B
н14
э
42 443 1442 443 1442 443 1442 443 1442 443 14442 4443 14442 4443 144442 44443 1442 443п
п
n tane
n tane
n tane
n tane
n tane
n tane
n tane
n tane п
п n tane
о
ю
olmak üzere, X rasgele değişkeni n denemede elde edilen başarı sayısı olsun.
X
0 başarı
1başarı
2 başarı
n- 1 başarı
n başarıь
пм
пп6447 448 64444444444447 4444444444448 64444444447 4444444448 644444444447 44444444448 6447 448ппп
W= н14
BB...44B3, 14
BB
BBB
BB42...44
BB
BBB
B ,..., 14442
BB...BBB
BB
BB
BB
BB
42...44B3, 144
42 ...
444B3,..., 144
43, 144
42 ...
4443
4443,..., 14
42...44B3, 14
42...44B3,..., 14
42...44B3, 14
42...44B3эп
пп 42
n tane
n tane
n tane
n tane
n tane
n tane
n tane
n tane
n tane
n tane п
п
оп
ю
R
0
1
2
...
n-1
n
X rasgele değişkeninin aldığı değerlerin kümesi,
DX = {0,1, 2,..., n - 1, n}
ve
P( X = 0) = P( BB
...B ) = qq
...q = q n
{
{
n tane
n tane
жц
n 1 n- 1
P( X = 1) = P( BB
...B veya BBB
B veya ... veya BB
BB3) = nq n- 1 p = зз ч
чp q
{
1442 ...
443
1442...44
ч
з ч
n tane
n tane
n tane
жц
зnч p 2 q n- 2
P( X = 2) = P( BBB
B veya ... vaya BB
...BBB
1442 ...
443
14442
4443) = зз ч
ч
ч
n tane
n tane
...
P( X = n) = P( BB
...B) = p n
{
n tane
olup, X in olasılık fonksiyonu,
n
f  x     p x q n  x , x  0,1,..., n
 x
dır. Moment çıkaran fonksiyon,
M X  t   E  etX    etx f  x 
n
x 0
x
n
     pet  q n  x
x 0  x 
n
  q  pet 
olmak üzere,
n
и2ш
и1 ш
EX  
EX
2
dM X  t 
t 0
dt

 n  q  pet 
d 2 M X t 
dt
2
t 0
n 1
pet
 np
t 0
 n  n  1  q  pet 
n2
 pe 
t
2
 n  q  pet 
n 1
pet
t 0
 n  n  1 p2  np
Var  X   E ( X 2 )  ( E ( X )) 2  n  n  1 p 2  np   np 
2
 np2  np  np 1  p   npq
dır.
Başarı olasılığı p olan bir Bernoulli denemesinin aynı şartlar altında, bağımsız olarak n kez
tekrarlanması deneyinde, yani bir Binom Deneyinde elde edilen başarı sayısı X rasgele değişkeni
olmak üzere, X e Binom Dağılımına sahiptir denir ve X : b(n, p) biçiminde gösterilir. n =1
için Binom Dağılımı bir Bernoulli dağılımıdır. Bernoulli Dağılımını b(1, p) biçiminde
gösterebiliriz.
Binom Dağılımında iki parametre bulunmaktadır. Birisi n (n О Z+ = {1, 2,3,...}, diğeri
p ( p О (0,1)МR) dir. Bu parametreleri bildiğimiz zaman, Binom Dağılımına sahip bir X rasgele
değişkeni ile ilgili olasılık, beklenen değer, varyans ve başka hesaplamalar yapabiliriz. Binom
Dağılımında parametre tahmini konusunu burada ele almayacağız. Parametre tahmini konusuna bu
ders yılı içinde sıkça değineceğiz, ancak parametre tahminini Lisans Eğitimi düzeyinde İST202
dersinde göreceksiniz. n =1 için Binom Dağılımı bir Bernoulli dağılımıdır. Bernoulli Dağılımını
b(1, p) biçiminde gösterebiliriz.
Örnek 1 Düzgün bir paranın üç kez atılışında örnek uzay,
  {YYY  YYT  YTY  TYY  YTT  TYT  TTY  TTT }
olmak üzere, X rasgele değişkeni üç atışta gelen turaların sayısı olsun. Böyle tanımlanan X
1
p=
rasgele değişkeni n = 3 ve
olan Binom Dağılımına sahiptir, yani
2
1
X : b(n = 3, p = ) dır. X rasgele değişkenin aldığı değerlerin kümesi,
2
DX  X ()  {01 2 3}
olmak üzere, X in olasılık fonksiyonu,
 3 1   1 
f  x       
 x 2   2 
x
3 x
, x  0,1, 2,3
ve olasılık tablosu
x
f ( x)  P( X  x)
0
1/8
1
3/8
dır. X rasgele değişkeninin dağılım fonksiyonu,
2
3/8
3
1/8
F : R ® [0,1]
м
0
п
п
п
п
1
п
п
п
8
п
п
п
4
x ® F ( x) = P( X Ј x) = п
н
п
8
п
п
п
7
п
п
п
8
п
п
п
п
о1
,
x< 0
, 0Ј x< 1
, 1Ј x < 2
, 2Ј x< 3
xі 3
,
dır. Olasılık fonksiyonu ile dağılım fonksiyonunun grafikleri,
f(x)
3/8
1/8
x
0
1
2
3
F(x)
1
7/8
o
4/8
1/8
o
o
o
0 1
x
2
3
ve
E  X   np =
3
= 1.5
2
Var  X   E ( X 2 )  ( E ( X )) 2  npq 
3
 0.75
4
dır.
Bir torbada eşit sayıda beyaz ve kırmızı top bulunsun. Çekileni yine torbaya atarak ardı
ardına üç top çekilmesi deneyinde gelen beyaz topların sayısı X rasgele değişkeni olsun.
1
X : b(n = 3, p = ) dır.
2
Aşağıdaki Matlab programını gözden geçiriniz.
>>x=0:3
x= 0
1
2
3
>> binopdf(x,3,1/2)
ans =
0.125
0.375
0.375
0.125
>> binocdf(x,3,1/2)
ans =
0.125
0.5
0.875
1
>> stairs(x,ans)
1
0.8
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
Örnek 2 Bir torna makinası bir günde 5 parça işlemektedir. Bir parçayı kusursuz olarak
4
işlemesi olasılığının p = olduğu bilinsin. Bir günde kusursuz olarak işlenen parça sayısı X
5
4
rasgele değişkeni olsun. X : b(n = 5, p = ) dağılımına sahiptir. X in olasılık fonksiyonu,
5
x
5 x
 5 4   1 
f  x         x  01 2 3 4 5
 x 5   5 
olasılık tablosu,
x
0
1
2
3
4
5
x
5 x
1
20
160
640
1280
1024
 5 4   1 
f  x       
3125
3125
3125
3125
3125
3125
 x 5   5 
>> x=0:5
x=
0
1
2
3
4
5
>> binopdf(x,5,4/5)
0.00032
0.0064
0.0512
0.2048
0.4096
0.32768
4
ve E ( X ) = np = 4 , Var ( X ) = npq = = 0.8 dır.
5
İşlenmemiş parçanın alış değeri a =100 TL, işleme masrafı b =100 TL, kusurlu işlenmiş
parçanın hurda değeri c =10 TL ve kusursuz işlenmiş parçanın satış değeri d =310 TL
olduğunda,
K  5(c  a  b)  (d  c) X  950  300 X
E ( K )  950  300 E ( X )  950  300  4  250
Var ( X )  3002Var ( X )  3002 
 X  72000  268.3
4
 72000
5
dır. Günlük kazancın beklenen değeri 250 TL dir. Günlük kazancın olasılık dağılımı,
x
0
1
3125
-950
1
3125
P( X  x)
k  950  300x
P( K  k )
1
20
3125
-650
20
3125
2
160
3125
-350
160
3125
3
640
3125
-50
640
3125
4
1280
3125
250
1280
3125
5
1024
3125
550
1024
3125
olmak üzere, bazı günlerde 550 TL kazanç olduğu gibi, 950, 650 ya da 350 TL kayıp söz
konusu olabilir.
Örnek 3 5 seçenekli 20 soruluk bir test sınavında sorular rasgele işaretlendiğinde,
a) En az 10 doğru cevap tutturma olasılığı nedir?
b) Tutturulan doğru cevap sayısının beklenen değeri nedir?
c) Her doğru cevap için 1 ve 4 yanlış cevap için -1 puan verildiğinde 20 soru
için beklenen puan nedir?
X-rasgele değişkeni işaretlenen 20 sorudan doğru cevaplananların sayısı olsun.
1
b(n=20, p = )
5
x
20  x
 20   1   4 
f  x         x  01 2 ..., 20
 x  5   5 
X
E ( X ) = np = 4
Var ( X ) = npq =
80
= 3.2
25
olmak üzere,
20
a) P( X і 10) =
е
x= 10
20- x
x
ж20ц
ж1 ц
ж4 ц
ч
з
ч
з
з ч
f ( x) = е з ч
ч
ч
з
чзи5 ши
ч зз 5 ш
ч
ч
з
x
и
ш
x= 10
20
= 0.0025948
Matlab kodu:
>>x=10:20;
>>sum(binopdf(x,20,1/5))
ans = 0.0025948
P( X і 10) = 1- P( X < 10) = 1- P( X Ј 9) = 1- F (9) =0.0025948
>> 1-binocdf(9,20,1/5)
ans = 0.0025948
b) E ( X ) = np = 4
c) K rasgele değişkeni 20 sorudan elde edilen puanı göstersin.
K = 1ґ X - 1/ 4ґ (20 - X ) =
5
X- 5
4
ve
E(K ) =
5
5
E( X ) - 5 = ґ 4 - 5 = 0
4
4
dır.
Örnek 4 4 çocuklu bir ailede kız çocukların sayısı X rasgele değişkeni olsun.
1
X b(n  4, p  )
2
olmak üzere,
x
4 x
 4 1   1 
1  4
f  x             x  01 2 3 4
16  x 
 x 2   2 
dır. Olasılık tablosu,
x
1  4
f  x   
16  x 
0
1
16
1
4
16
2
6
16
3
4
16
4
1
16
ve
E ( X ) = np = 2
,
Var ( X ) = npq = 1
dır. 4’er çocuklu 160 ailenin kız çocuk sayısı bakımından dağılışı ne olur?
kız çocukların sayısı
0
1
2
3
4
aile sayısı (teorik sıklık , frekans)
10=160  P(X=0)
40=160  P(X=1)
60=160  P(X=2)
40=160  P(X=3)
10=160  P(X=4)
160
Örnek 5 3 beyaz ve 2 siyah top bulunan bir kavanozdan iadeli olarak 10 kez top çekildiğinde,
a) Gelen siyah topların sayısının beyazlardan çok olması olasılığı nedir?
b) Siyah topların beklenen sayısı nedir?
c) Siyah top için 100 TL kazanılsa, beyaz top için 50 TL kaybedilse, böyle bir oyunda
kazancın beklenen değeri nedir?
X-rasgele değişkeni 10 çekilişte gelen beyaz topların sayısı olsun.
X
3
b(n=10, p = )
5
10   3 
f  x     
 x  5 
x
10  x
2
 
5
 x  01 2 ...,10
E ( X ) = np = 6
Var ( X ) = npq = 2.4
>>x=0:10
>> binopdf(x,10,3/5)
ans =
0.00010486 0.0015729
0.010617
0.042467
0.11148
0.20066
0.25082
0.21499
0.12093
0.040311 0.0060466
olmak üzere,
10- x
ж10ч
цж3 цx ж2 ц
з
з ч
з ч
a) P( X < 5) = P( X Ј 4) = е з ч
ч
ч
чззи5 ши
ч зз 5 ш
ч
з ч
x= 0 иx ш
4
= 0.00010486+0.0015729+0.010617+0.042467+0.11148
=0.16624
>>x=0:4;
>> sum(binopdf(x,10,3/5))
ans =
0.16624
10- x
ж10ч
цж3 цx ж2 ц
з
з ч
з ч
P( X < 5) = P( X Ј 4) = F (4) = е з ч
ч
ч
чззи5 ши
ч зз 5 ш
ч
з ч
x= 0 иx ш
4
>> binocdf(4,10,3/5)
ans =
0.16624
b) E ( X ) = np = 6
c) K rasgele değişkeni kazanç olsun.
K = - 50 X + 100(10 - X ) = - 150 X + 1000
ve
E ( K ) = - 150 E ( X ) + 1000 = 100
dır.
= 0.16624
Oran Tahmini
(Bernoulli Dağılımında Parametre Tahmini)
(İadeli Çekilişler)
Buraya kadar çözdüğümüz problemlerde başarı olasılığı p’nin bilindiğini varsaydık.
Bir Bernoulli denemesinde p ( 0  p  1 ) başarı olasılığı bilinmediğinde ne yapacağız? Örneğin,
içinde bilinmeyen sayıda beyaz ile siyah top bulunan ve içine bakmamıza müsaade edilmeyen
bir torbadan (kitleden) rasgele bir top çekilişinde beyaz top gelmesi olasılığı p (kitle oranı)
bilinmemektedir. Torbadan iadeli olarak (çekileni geri atarak) birer birer top çekilmesine
müsaade edilse ne yaparız? Torbadan n kez top çekip, gelen beyaz top sayısı X=x değerini
gözleyip, gözlenen x/n oranını bilinmeyen p kitle oranı için bir “tahmin” olarak alırız.
Örneğin 20 çekilişte 8 kez beyaz top gelirse, p için bir “tahmin”=8/20=0.40 olur. Yeniden 20
çekiliş yapıldığında gelen beyaz top sayısı yine 8 mi olur? Muhtemelen farklı olur. Sezgimiz,
20 yerine 100 çekiliş yapılırsa p için elde edilecek “tahmin” ‘in daha “iyi” olacağını
söylemektedir. Şimdilik sezgimize güvenelim ve bilinmeyen bir p başarı olasılığını (oranını)
“tahmin” etmek için
X
Başarı Sayısı
=
n
Deneme Sayısı
rasgele değişkenini kullanalım. Bununla birlikte, sezgimizin ötesinde bazı değerlendirmeler
yapabiliriz. Örneğin, torbada 3 beyaz (300 beyaz)ve 2 sarı (200 sarı) top bulunduğunda, iadeli
3
olarak yapılan n=20 çekilişte gelen beyaz top sayısı X olmak üzere, X : b(n = 20, p = )
5
olup, X rasgele değişkenin olasılık dağılımı,
>> x=0:10
x=0
1
2
3
4
5
6
7
8
9
10
>> binopdf(x,20,3/5)
0.0000
0.0000
0.0000
>> x=11:20
x = 11
12
13
>> binopdf(x,20,3/5)
0.1597
0.1797
0.165 9
0.0000
14
0.1244
0.0003
0.0013
0.0049
0.0146
15
16
17
0.0747
0.0350
0.0124
0.0355
18
0.0031
0.0710
0.1171
19
20
0.0005
0.0000
X
dır.
rasgele değişkeninin [0.50,0.70] aralığında çıkması olasılığı, X rasgele değişkeninin
n
[10,14] aralığında çıkması olasılığı kadar olup, bu olasılık 0.7469 dır.
X
P(0.50 Ј
Ј 0.70) = P(10 Ј X Ј 14) = 0.7469
n
olmak üzere, gerçekte p=3/5=0.60 olan değer %75 olasılıkla 0.50, 0.55, 0.60, 0.65, 0.70
değerlerinden biri olarak tahmin edilecektir.
X
P(0.45 Ј
Ј 0.75) = P(9 Ј X Ј 15) = 0.8925
n
olmak üzere, gerçekte p=3/5=0.60 olan değer %89 olasılıkla 0.45, 0.50, 0.55, 0.60, 0.65, 0.70,
0.75 değerlerinden biri olarak tahmin edilecektir.
20 çekiliş yerine 100 çekiliş yapılırsa,
X
P(0.55 Ј
Ј 0.65) = P(55 Ј X Ј 65) = 0.9685
n
>> x=50:70; sum(binopdf(x,100,3/5))
ans = 0.96846
olmak üzere, gerçekte p=3/5=0.60 olan değer %97 olasılıkla 0.50, 0.51, 0.52, ..., 0.68, 0.69,
0.70 değerlerinden biri olarak tahmin edilecektir.
X : b(n = 100, p = 3 / 5) rasgele değişkeni ile
X
n
rasgele değişkeninin olasılık
fonksiyonlarının grafikleri aşağıdadır.
0.1
0.08
0.06
0.04
0.02
0
0
10
20
30
40
50
60
70
80
90
100
0.5
0.6
0.7
0.8
0.9
1
>> x=0:100 ; plot(x,binopdf(x,100,3/5),'.')
0.1
0.08
0.06
0.04
0.02
0
0
0.1
0.2
0.3
0.4
>> x=0:100 ; plot(x/100,binopdf(x,100,3/5),'.')
Bilinmeyen bir p kitle oranını, iadeli çekilişler yaparak
X
Başarı Sayısı
=
ile
n
Deneme Sayısı
X
rasgele değişkeninin alacağı değerlerin p değerine “yakın
n
X
düşmelerini” isteriz. Yukarıda bunu irdelemeye çalıştık.
rasgele değişkenine p için bir
n
X
tahmin edici diyelim.
tahmin edicisi için
n
жX ц 1
жX ц 1
1
1
pq
E зз ч
= E ( X ) = ґ np = p = 0.60 , Var зз ч
= 2 Var ( X ) = 2 ґ npq =
ч
ч
ч
ч
зи n ш n
зи n ш n
n
n
n
olmak üzere, tahmin edicinin beklenen değeri p parametresine eşittir. Böyle bir tahmin
ediciye yansız tahmin edici diyeceğiz. Oran tahmininde yapmaya çalıştığımız bu düşünceleri
ileride Parametre Tahmini olarak göreceğiz. İstatistikçilerin yaptığı işlerden biri Parametre
Tahmini diğeri de Hipotez Testidir. Biraz da ikincisine değinelim.
tahmin etmek istediğimizde,
Oran İle İlgili Hipotez Testi
Bir torbada 2:3 oranında iki renkten (beyaz ve siyah) toplar bulunmaktadır. İki kişiden
biri beyazların tüm toplara oranının 3/5, diğeri ise 2/5 olduğunu iddia etmektedir. Torbaya
bakmaksızın, iadeli olarak top çekerek hangisinin haklı olduğu nasıl söylenebilir? Öne sürülen
iddialar (hipotezler),
3
H 0 : Torbadaki beyaz topların tüm toplara oranı p = dır.
5
2
H1 : Torbadaki beyaz topların tüm toplara oranı p = dır.
5
şeklinde yazılsın. Hangi hipotezin doğru olduğunu ortaya çıkarmak için iadeli olarak 20 top
çekip, gelen beyaz top sayısı olan X rasgele değişkenine bağlı olarak:
* X і 10 olursa H 0 kabul edilsin
* X < 10 olursa H1 kabul edilsin
başka bir ifade ile,
X
* і 0.50 olursa H 0 kabul edilsin
20
X
* < 0.50 olursa H1 kabul edilsin
20
gibi bir karar kuralı oluşturulsun. Bu karar kuralına göre, H 0 doğru ( X : b(n = 20, p =
3
))
5
iken, gözlemlerdeki rasgelelikten dolayı reddedilmesi olasılığı,
P( X < 10) = %13
>> x=0:9;
>> sum(binopdf(x,20,3/5))
ans = 0.12752
ve H1 doğru ( X : b(n = 20, p =
2
) ) iken, gözlemlerdeki rasgelelikten dolayı reddedilmesi
5
olasılığı,
P( X і 10) = %24
>> x=10:20;
>> sum(binopdf(x,20,2/5))
ans = 0.24466
dır. H 0 doğru iken reddedilmesi olayına 1. tip hata, H1 doğru iken reddedilmesi olayına 2.
tip hata denir. Buna göre, yukarıdaki karar kuralı için 1. tip hata yapma olasılığı,
P( H 0 ' ın reddedilmesi / H 0 doğru) =%13
ve 2. tip hata yapma olasılığı,
P( H1 ' in reddedilmesi / H1 doğru) =%24
dır.
100 kez çekiliş yapıp, gelen beyaz top sayısı olan X rasgele değişkenine bağlı olarak:
* X і 50 olursa H 0 kabul edilsin
* X < 50 olursa H1 kabul edilsin
gibi bir karar kuralı oluşturulursa,
x=0:49;
>> sum(binopdf(x,100,3/5))
ans = 0.016762
P( H 0 ' ın reddedilmesi / H 0 doğru) =%2
>> x=50:100;
>> sum(binopdf(x,100,2/5))
ans = 0.027099
P( H1 ' in reddedilmesi / H1 doğru) =%3
olur.
Örnek 6 Bir portakal üreticisi işçilerine 800 kasa vaşington portakalı ile 200 kasa başka bir
portakalı karıştırarak harmanlamalarını söylemiştir. Bir alıcı, işçilerin 700 kasa vaşington
portakalının arasına 300 kasa diğer portakaldan karıştırdıklarını iddia etmektedir. Ortaya,
H 0 : p = 0.80
H1 : p = 0.70
hipotezleri atılmıştır. Dış görüntüleri aynı olan portakalları ayırt etmek için laboratuar
kontrolü gerekmektedir. Rasgele seçilen 100 portakal kontrol edilecektir. X rasgele
değişkeni, seçilen 100 portakal içinde vaşington olanların sayısı olsun. (Önümüzdeki derste
göreceğimiz gibi, çekilişler iadeli yapılmamış olsa bile yığındaki portakal sayısı çok fazla
olduğundan X rasgele değişkeninin Binom Dağılımına sahip olduğunu söyleyebiliriz.
Şimdilik, çekilişler iadeli gibi yapılmış sayılsın.)
X rasgele değişkenine bağlı olarak:
* X і c olursa H 0 kabul edilsin
* X < c olursa H1 kabul edilsin
gibi bir karar kuralı üzerinde durulmaktadır. Satıcı: “Ben haklı isem, gözlemlerdeki
rasgelelikten dolayı haksız çıkarılmam olasılığı %5 i geçmesin” demektedir. Kısaca,
P( H 0 ' ın reddedilmesi / H 0 doğru) Ј %5 = a
yani, X : b(n = 100, p = 0.80) iken,
P( X < c) Ј 0.05
olacak şekilde bir c sayısı belirleyin demektedir.
>> x=75:100 ; sum(binopdf(x,100,.70))
ans = 0.16313
>> x=0:74 ; sum(binopdf(x,100,.80))
ans = 0.087475
>> x=0:73 ; sum(binopdf(x,100,.80))
ans = 0.055833
>> x=0:72 ; sum(binopdf(x,100,.80))
ans = 0.034152
olmak üzere,
P( X < 73) Ј 0.034152
dır. c=73 alınıp,
* X і 73 olursa H 0 kabul edilsin
* X < 73 olursa H1 kabul edilsin
gibi bir karar kuralı oluşturulursa, satıcının isteği yerine gelmektedir. Birinci tip hata yapma
olasılığı,
P( H 0 ' ın reddedilmesi / H 0 doğru) =0.034152
olup, %5 den küçüktür. İkinci tip hata yapma olasılığına gelince, H1 doğru, yani
X : b(n = 100, p = 0.70) ) iken, gözlemlerdeki rasgelelikten dolayı H1 in reddedilmesi
olasılığı,
P( H1 ' in reddedilmesi / H1 doğru) = P( X і 73) = 0.29637
>> x=73:100; sum(binopdf(x,100,.70))
ans = 0.29637
dır.
H 0 : p = 0.80 ve H1 : p = 0.70 hipotezleri altında, X rasgele değişkeninin olasılık
fonksiyonun grafikleri aşağıdaki gibidir.
>> x=0:100;
>> plot(x,binopdf(x,100,.7),'.')
>>hold on
>> plot(x,binopdf(x,100,.8),'.r')
0.1
0.08
0.06
0.04
0.02
0
0
10
20
30
40
50
60
0.034152
70
80
90
100
0.29637
Hipotez testinde öne sürülen iki hipotez söz konusu olup, belli bir karar verme
kuralına göre, gözlemlere dayalı olarak, hangisinin reddedileceğine karar verilmektedir. Karar
kuralı, önceden belirlenmiş hata yapma olasılıkları çerçevesinde bir rasgele değişken (test
istatistiği) üzerine kuruludur. Hipotez testine önümüzdeki derslerde de değineceğiz. Lisans
Eğitimi düzeyinde hipotez testini İST202 dersinde göreceksiniz.