STATİK

1
STATİK- MUKAVEMET
Düzlem ve Uzay Kuvvetler
2.1 Kuvvet vektörü ve kuvvein Tanımı
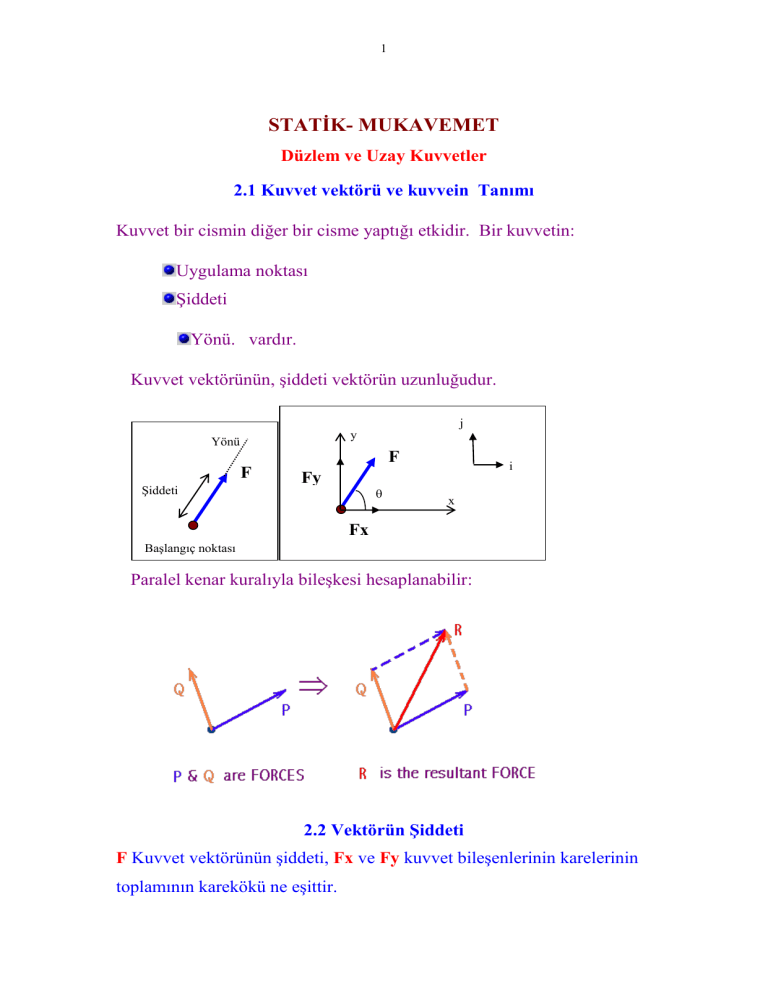
Kuvvet bir cismin diğer bir cisme yaptığı etkidir. Bir kuvvetin:
Uygulama noktası
Şiddeti
Yönü. vardır.
Kuvvet vektörünün, şiddeti vektörün uzunluğudur.
j
y
Yönü
F
F
Şiddeti
Fy

i
x
Fx
Başlangıç noktası
Paralel kenar kuralıyla bileşkesi hesaplanabilir:
2.2 Vektörün Şiddeti
F Kuvvet vektörünün şiddeti, Fx ve Fy kuvvet bileşenlerinin karelerinin
toplamının karekökü ne eşittir.
2
Fx=F cos Fy=F sins
tan=Fy/Fx,
F  Fx2  Fy2  
2.3 Vektörlerin Toplamı
P ve Q vektörünün toplamı R vektörü aşağıdaki gibi hesaplanabilir.
  
PQ  R
Px i  Py j  Q x i  Q y j  R x i  R y j
( Px  Q X )i  ( PY  Q y ) j  R x i  R y j
Rx=Px+Qx,
Ry=Py+Qy
Rx   Fx ,
R y   Fy
R  Rx i  R y j
R 2  F12  F22  2F1 F2 cos 
2.4 Üç Boyutlu Uzayda Kuvvet Bileşenleri
3
Üç Boyutlu uzayda F kuvvetinin bileşenleri, Fx, Fy, Fz kuvvetleridir.
F  Fy2  Fh2 , Fh  Fx2  Fz2
4
F  Fx2  Fy2  Fz2
i, j, k vektörler ; x,y,z eksenlerinin birim vektörleridir.

F  Fxi  Fy j  Fz k

F  F cos  x i  cos  y j  cos  z k 

F  F  x i   y j   z k 


F  F
Landa birim vektördür
2  cos 2  x  cos 2  y  cos 2  z
 1
cos 2  x  cos 2  y  cos 2  z  1
Iki açı bağımsız, 3. açı diğer açılara bağımlı
Üç boyutlu uzayda F kuvveti aşağıdaki şekilde tanımlanabilir.
5




AB  d xi  d y j  d z k
dx=x2-x1,
dy=y2-y1, dz=z2-z1
d, AB doğrusunun uzunluğu




AB 1

 (d x i  d y j  d z k )
AB d

AB  d x2  d y2  d z2
 F




F  F  (d x i  d y j  d z k )
d
Fx 
cos  x 
Fd z
Fd y
Fd x
, Fy 
, Fz 
d
d
d
dy
dx
 y ,
  x , cos  y 
d
d
cos  z 
dz
 z
d
2.5 Üç boyutlu uzayda kuvvetlerin toplamı, ve denge denklemleri


R  F ,
6
Rx   Fx ,
R y   Fy ,
Rz   Fz
R  Rx2  R y2  Rz2


R  F  0,
Rx   Fx  0 , Ry   Fy  0 ,
Rz   Fz  0
7
Örnek:
8
Örnek:
Cevap
1. adım
:
Serbest cisim diyagramı
Eleman uzunlukları
9
2. Adım
Her elemanın x , y, z yönündeki kuvvetleri
3. Adım
Denge denklemleri ve sonuçlar
10
2.6 Bir Kuvvetin Bir Noktaya Göre Momenti
Kuvvet vektörü F, konum vektörü r ile vektörel çarpımdır.

 
M 0  r xF
Momentin şiddeti
M0=FrsinF.d
F Kuvvetinin Ekseni
O
F
r
d
F


F||
11
Örnek 1. Diagram 3, te 10 foot uzunluğundaki kiriş, P noktasında
bağlıdır, 100 lb. Kuvvet kirişe yukarı doğru etkimektedir
Moment = F x d = 100 lb. x 10 ft = 1000 ft-lb.
2.5 foot mesafeden etkirse
Moment = F x d = 100 lb. x 2.5 ft. = 250 ft-lb.
Örnek 2: Bu örnekte kuvvet 37 derece açı ile etkimektedir.
Moment = Kuvvet x dik mesafe
d = 10 sin 37o = 6 ft,
Moment = 100 lb. x 6 ft = 600 ft-lb.
Veya kuvvet iki bileş ene ayrı lı r
12
Moment = 100 lb. sin 37o x 10 ft. = 600 ft-lb
2.7 Vektörel Çarpım:
  
V  PxQ
Özellikleri
-1 V vektörü, P ve Q vector düzlemine diktir.
-2 V nin Şiddeti V=PQsin
-3 V vektörünün yönü sağ el kuralına uyuyor.
 
 
PxQ  (QxP)
13
2.8 Birim vektörlerin vektörel çarpımları:
14
15
2.9 VARIGNON prensibi:
16
2.10 Momentin üç boyutlu uzaydaki gösterimi
17
2.11 iki vektörün skaler çarpımı:
Şekil Skaler çarpımın geometrik anlamı
18
19
2.12 Bir kuvvetin, bir eksene gore momenti
F Kuvvetinin a-a eksenine gore Momenti
20
2.13 Kuvvet Çifti
M=F.d
21
22
2.13 Bir Kuvvetin Tesir Çizgisi Dışında Bir Noktaya Taşınması
2.15 Kuvvetler Sisteminin Bir Noktaya İndirgenmesi
n
R x   ( Fi ) x ,
i 1
n
M o   (M i ) x
i 1
23
ÖRNEK SORULAR
Öğrenci No 010030403
---------------xaxxbxcde
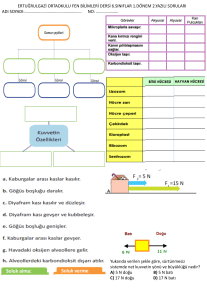
1Şekildeki kuvvetler sisteminin bileşkesi
düşey olabilmesi için  ne olmalıdır.
a) F=240N,
120N
60o
80N

F
Çözüm
Rx=0 olmalı
a)
Rx=240cos-120-80cos60=0
Cos=2/3,
=48.20
b) F=140N
24
b)
Rx=140cos-120-80cos60=0
Cos=8/7> 1 olduğundan, bu mümkün değil
2-
Şekildeki blokların boyutları 90cm120cm, ağırlıkları 10kN ve halat
uzunlukları da 150cm olduğuna
göre, her iki durumda da halatlardaki
çekme kuvvetlerini bulunuz
I
II
1. Durum
W
75cm

45cm
S2
S1
Cos=45/75=0.6
=53.13
Yatay Dengeden S1=S2
Sinüs teoreminden
W/(sin(2x53.12))=S1/sin36.87
W=10kN
S1=S2=6.25kN
2. Durum
25
W
75cm

S2
S1
60cm
Cos=60/75=0.8
=36.87
Yatay Dengeden S1=S2
Sinüs teoreminden
W/(sin(2x36.87))=S1/sin53.13
W=10kN
S1=S2=8.33kN
y
A(4;4)
3
C(-2;2)
4
100kN
B(2;2)
80kN
50kN
x
0
D(4;0)
Rx=100-40=60kN
Ry=-80-30=-110
R=125.3kN
Md=80x2-100x4+40x2+30x6
Md=20kNm
M0=xRy-yRx
Mo=-80x2-100x4+30x2+40x2
Şekildeki kuvvetler sistemini D
noktasına indirgeyiniz
Tesir Çizgisinin denklemini
yazınız
26
Mo=-420kNm
60y=-110x+420
x=0 için y=7
y=0 için x=3.82
Herbir yatay çizginin arası a
ise, Aşağıdaki hangi kuvvet
sistemi
yandaki
kuvvet
sistemine eş değerdir.
P
M=Pa
P, Q ve S birer vektör olmak üzere
aşağıdakilerden hangisi yanlıştır
A)
(P+Q)+S=(P+S)+Q
B)
(PxQ)+S=S+(PxQ)
C)
(PxQ)= - (QxP)
D)
(PxQ)xS=Px(QxS)
B)
A)
P
P
P
C)
D)
P
z
M=4 kNcm
A) A noktasına Fy=2kN, B noktasına Fy=-2kN
B) A noktasına Fy=-2kN, B noktasına Fy=2kN
C) B noktasına Fx=2kN, C noktasına Fx=-2kN
D) B noktasına Fx=-2kN, C noktasına Fx=2kN
A
B
C
M momenti için hangi kuvvet
çifti gerekir
y
4
2
x
4
y
x
Kenar uzunlukları 2cm olan altı gen
şekilindeki levhaya etkiyen kuvvetler
sistemini
A) O noktasına indirgeyiniz.
B) Bileşkenin etki çizgisinin x ve y
eksenlerini kestiği noktaları bulunuz.
bulunuz.
P=(a+b+c+d+e) kN
Üç boyutlu uzayda bir vektörün x ve y
eksenleriyle yaptığı açı 45 derece
olduğuna göre z ekseniyle yaptığı açı kaç
derece olabilir.
sin 45  cos 45  2 / 2
A) 0, B) 45 C) 90 D)180