TRiGONOMETRi DERS NOTUHAZIRLAYAN

TRiGONOMETRi DERS NOTU HAZIRLAYAN:
Yemlüha ONAT
www.yemluhaonat.tr.cx
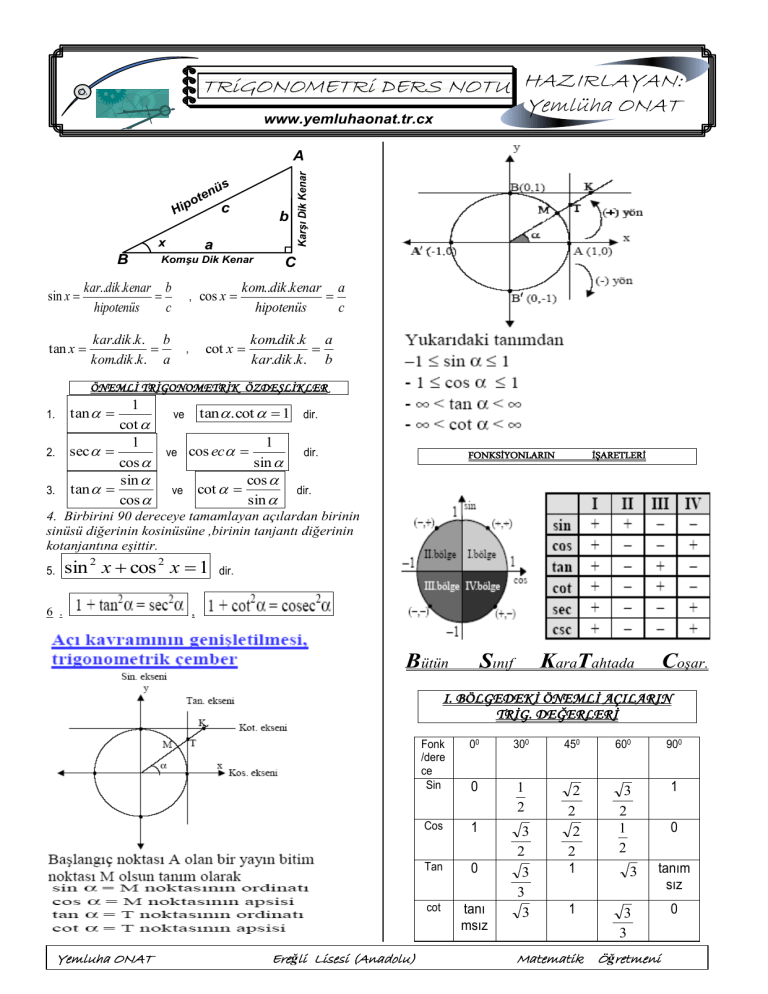
H
üs
ten
o
ip
c
x
B
sin x 
a
Komşu Dik Kenar
kar..dik .kenar b

hipotenüs
c
tan x 
b
kar.dik .k. b

kom.dik .k. a
,
cos x 
C
kom..dik .kenar a

hipotenüs
c
cot x 
,
Karşı Dik Kenar
A
kom.dik .k a

kar.dik .k. b
ÖNEMLİ TRİGONOMETRİK ÖZDEŞLİKLER
1
ve tan  . cot   1 dir.
cot 
1
1
2. sec  
ve cos ec 
dir.
cos 
sin 
sin 
cos 
3. tan  
ve cot  
dir.
cos 
sin 
tan  
1.
FONKSİYONLARIN
İŞARETLERİ
4. Birbirini 90 dereceye tamamlayan açılardan birinin
sinüsü diğerinin kosinüsüne ,birinin tanjantı diğerinin
kotanjantına eşittir.
sin 2 x  cos 2 x  1
5.
6 .
dir.
,
Bütün
Sınıf
KaraTahtada
Coşar.
I. BÖLGEDEKİ ÖNEMLİ AÇILARIN
TRİG. DEĞERLERİ
Yemluha ONAT
Ereğli Lisesi (Anadolu)
Fonk
/dere
ce
Sin
00
300
450
600
0
1
2
Cos
1
3
2
1
2
Tan
0
2
2
2
2
1
cot
tanı
msız
3
2
3
3
3
1
3
900
1
0
tanım
sız
3
3
Matematik Öğretmeni
0
TERS DÖNÜŞÜM FORMÜLLERİ:
1
sin x. cos y  .[sin( x  y )  sin( x  y )]
2
1
cos x. sin y  .[sin( x  y )  sin( x  y )]
2
1
cos x. cos y  .[cos( x  y )  cos( x  y )]
2
1
sin x. sin y   .[cos( x  y )  cos( x  y )]
2
Toplam ve Fark Formülleri:
sin( x  y)  sin x. cos y  cos x. sin y
sin( x  y)  sin x. cos y  cos x. sin y
cos( x  y)  cos x. cos y  sin x. sin y
cos( x  y)  cos x. cos y  sin x. sin y
tana+tanb
tan(a+b)=
1- tana.tanb
tana - tanb
tan(a - b)=
1+tana.tanb
TRİGONOMETRİK ÖZDEŞLİKLER
Yarım Açı Formülleri:
Toplam ve fark formüllerinde y=x yazılırsa
aşağıdaki yarım açı formülleri elde edilir.
1) Cos2 +Sin2 = 1
2) Tan .Cot
3) 1 + Tan2 = Sec2
4) 1 + Cot2 = Csc2
5)
sin 2 x
cos 2 x
tan 2 x
tan  
2.sin x.cos x
2
2
cos x sin x
2
2
2 cos x 1 1 2.sin x
2 tan x
1 tan 2 x
cot 2 x
cot  
6)
cos 
sin 
4Sin3 x
7*) Sin3x
3Sinx
8*) Cos3x
4Cos 3 x 3Cosx
cot 2 x 1
2 cot x
Dönüşüm –Ters Dönüşüm Formülleri:
sin 
cos 
=1
Üçgende Trigonometrik Bağıntılar
Cosinüs teoremi : a2 = b2 + c2 -2bcCosA
Toplam ve fark formülleri taraf tarafa toplanıp çıkarıldığında dönüşüm ve ters –dönüşüm formülleri elde edilir.
DÖNÜŞÜM FORMÜLLERİ:
sin x
sin y
sin x sin y
cos x
cos y
cos x cos y
2.sin
2.cos
x
y
2
x
y
.cos
.sin
y
2
x
A( ABC )
y
2
2
x y
x y
2.cos
.cos
2
2
x y
x y
2.sin
.sin
2
2
sin( x  y )
tan x  tan y 
cos x. cos y
sin( x  y )
tan x  tan y 
cos x. cos y
sin( x  y )
cot x  cot y 
sin x. sin y
sin( x  y )
cot x  cot y 
sin x. sin y
Yemluha ONAT
Üçgenin Alanı:
x
1
.b.c.sin A
2
1
.a.c.sin B
2
1
.a.b.sin C
2
Trigonometrik Denklemlerde Kök formülleri :
1. Sin  Sin      k 2         k 2
2. Cos  Cos      k 2      k 2
3. Tan  Tan ve Cot  Cot      k

4. Sin  Cos   Sin  Sin    
2


5. Sin  Sin  Sin  Sin  
6. Tan  Tan ve Tan  Tan  
7. Cos  Cos ve Cos  Cos     Cos   
Ereğli Lisesi (Anadolu)
Matematik Öğretmeni