4
DENK KUVVET SİSTEMLERİ
BU BÖLÜMDE;
a) Moment kavramının tanımı, bir kuvvetin bir noktaya ve eksene göre momentinin nasıl
belirleneceği,
b) Rijit bir cisim üzerine etki eden kuvvetlerin etkisinden ve verilen bir kuvvet sisteminin daha
basit denk bir sistem ile nasıl değiştirileceğinden bahsedilecektir.t
İKİ VEKTÖRÜN VEKTÖR ÇARPIMI
Bir kuvvetin bir noktaya göre momenti kavramı vektör çarpımı uygulamalarıyla daha iyi
anlaşılabilir. Bu yüzden burada öncelikle vektörel çarpım konusuna değinilecektir.
A ve B vektörlerinin vektör çarpımı aşağıdaki şartları sağlayan C vektörü
olarak tanımlanır:
C vektörünün etki çizgisi A ve B vektörlerinin yer aldığı düzleme diktir
ve doğrultusu sağ el kuralından bulunur.
C vektörünün büyüklüğü; C = AB sinθ
C A B AB sin uC
(0° ≤ θ ≤ 180°)
Vektör çarpımlarının değişme özelliği yoktur.
A B B A
Vektör çarpımlarının dağılma özelliği vardır.
P Q1 Q 2 P Q1 P Q 2
Vektör çarpımlarının birleşme özelliği yoktur.
PQ S P QS
KARTEZYEN VEKTÖRLERİN VEKTÖR ÇARPIMI
k i j
j
i j i. j. sin 90 1.1.1 1
i i i.i. sin 0 1.1.0 0
i
i
i i 0
i j k
i k j
j i k k i j
j j 0
k j i
j k i
k k 0
j
k
A ve B vektörel çarpımı;
A Ax i Ay j Az k
B Bx i B y j Bz k
A B Ax i Ay j Az k Bx i B y j Bz k
A B Ay Bz Az B y i Ax Bz Az Bx j Ax B y Ay Bx k
AXB Ax
j
k
Ay
Az
Bx
By
Bz
i
Bir Kuvvetin Bir Noktaya Göre Momenti – Skaler Gösterim
Bir kuvvetin bir noktaya veya bir eksene göre momenti, kuvvetin bir cismi bu nokta veya eksen etrafında
döndürme eğiliminin bir ölçüsüdür.
Eğer kuvvet düzlem cismi saat
yönünün tersine döndürmeye
eğilimli ise moment vektörünün
yönü düzlem dışına doğrudur ve
pozitif büyüklüktedir.
Eğer kuvvet düzlem cismi saat
yönünde döndürmeye eğilimli ise
moment vektörünün yönü düzlem
içine
doğrudur
ve
negatif
büyüklüktedir.
M o F .d
Aynı noktadan geçen bir çok kuvvetin bileşkesinin belirli bir O
noktasına göre momenti; farklı kuvvetlerin aynı O noktasına göre
olan momentlerinin toplamına eşittir.
M R O Fd
MO 100N 2m 200N m
MO 50N 0.75m 75N m
Örnek 1: Şekilde gösterilen çubuk üzerine dört noktadan
kuvvete maruzdur. Bu kuvvetlerin O noktasında
oluşturacağı bileşke momenti bulunuz.
Bir Kuvvetin Bir Noktaya Göre Momenti – Vektörel Gösterim
F kuvveti, büyüklüğünü ve doğrultusunu tarif eden bir vektör ile
temsil edilebilir. Ancak bir kuvvetin rijit cisim üzerindeki etkisi
uygulanma noktasına da bağlıdır. F’nin O noktasına göre momenti,
MO r F
Momentin yönü sağ el kuralı ile belirlenebilir. MO ‘nun
doğrultu ve yönü, sağ el kuralıyla belirlenir. Buna göre r’yi
kesikli çizgili konuma uzatır ve sağ el parmaklarını r’den F’ye
doğru kıvırırsak, r başparmak yukarıya ya da r ve F’ yi içeren
düzleme dik yönlenir. Büyüklüğü ise,
M O rF sin Fd
Kuvvetin Taşınabilirliği
M O rA F
M O rB F
M O rC F
M O rB F rC F rA F
F kayan vektör özelliğine sahiptir. Yani etki çizgisi üzerinde
herhangi bir noktaya etkiyebilir ve O noktasına göre aynı
momenti üretir.
Bir Kuvvetin Momentinin Dik Bileşenleri
r xi yj zk
MO r F
i
j
k
F Fx i Fy j Fz k
M O M xi M y j M z k
MO x
y
z yFz zFy i zFx xFz j xFy yFx k
Fx
Fy
Fz
F Fx i Fy j Fz k
M B rA / B F
rA / B rA rB x A xB i y A y B j z A z B k
i
M B x A xB
Fx
j
k
Fy
Fz
y A yB z A z B
Kuvvetler Sisteminin Bileşke Momenti
M RO r F
Örnek 1: Şekilde gösterilen ağaç A noktasından bir halatla traktöre
bağlanmıştır. Traktörün halatta oluşturduğu kuvvetin şiddeti 2 kN
olduğuna göre, uygulanan kuvvetin O noktasına göre oluşturacağı
momenti Kartezyen vektör olarak belirleyiniz.
A(0, 0, 12)
rAB xB x A i y B y A j z B z A k
B(4, 12, 0)
4 i 12 j 12 k
rAB
4 i 12 j 12 k
u AB
0.2294 i 0.6881 j 0.6881 k
rAB
4 2 12 2 (12) 2
F F .u AB 2.(0.2294 i 0.6881 j 0.6881 k )
F 0.4588 i 1.376 j 1.376 k
M O rA F
M O rB F
M O rA F
i
j
k
0
0
12
rA 12 k
rB 4i 12 j
0.4588 1.376 1.376
0 (1.376) 12 1.376 i 0 (1,376) 12 0.4588 j
0 1.376 0 0.4588 k
M O 16.5i 5.51 j
M O rB F
i
j
k
4
12
0
0.4588 1.376 1.376
M O 16.5i 5.51 j
Örnek 2: Şekilde gösterilen çubuk üzerine iki adet kuvvet etki
etmektedir. Bu kuvvetlerin O noktasına göre oluşturacağı
moment vektörünü ve doğrultusunu belirleyiniz.
rA 5 j
rB 4i 5 j 2k
M RO r F rA F1 rB F2
i
M RO 0
j
k
i
j
k
5
0 4
5
2
60 40 20 80 40 30
30i 40 j 60 k N.m
M RO
30 i 40 j 60 k
u
0.3841 i 0.5122 j 0.7682 k
M RO
30 2 (40) 2 60 2
cos 0.3841
67.4o
cos 0.5122
121o
cos 0.7682
39.8o
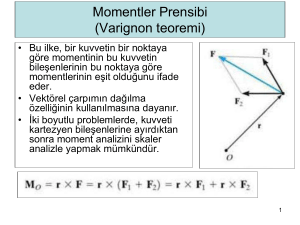
Momentler İlkesi (Varignon Teoremi)
M O r F r F1 F2
M O r F1 r F2
F F1 F2
Bir kuvvetin bir noktaya göre momenti, bu kuvvetin bileşenlerinin
o noktaya göre momentlerinin toplamına eşittir.
Örnek 3: F kuvveti yandaki şekilde gösterilen desteğin
köşesinde etki etmektedir. Bu kuvvetin O noktasına göre
oluşturacağı momenti belirleyiniz.
Skaler Çözüm:
Vektörel Çözüm:
Bir Kuvvetin Belirli Bir Eksene Göre Momenti: Bir kuvvetin bir noktaya göre momenti
hesaplanırken, moment ve moment ekseni, kuvvet ve moment kolunu içeren düzleme daima diktir.
Bazı problemlerde bu momentin söz konusu noktadan geçen belirli bir eksen üzerindeki bileşenini
bulmak önemlidir.
Vektörel Analiz
Skaler Analiz
MO r F
MO F d
M y j MO j r F
M y M O cos F d cos F d x
F F k
r d x i d y j
M y j d x i d y j F k
M y F dx
M a ua M O ua r F
MO r F
i
k
j
i
j
k
M a ua rx
ry
rz ua x i ua y j ua y k rx
ry
rz
Fx
Fy
Fz
Fy
Fz
Fx
uax
M a ua r F rx
Fx
ua y
ua y
ry
rz
Fy
Fz
Örnek 4: F kuvveti yandaki şekilde gösterilen desteğin A
noktasına etki etmektedir. Bu kuvvetin x ve OB
eksenlerine göre oluşturacağı momenti belirleyiniz.
Örnek 5: F kuvvetinin OA eksenine göre oluşturacağı momenti belirleyiniz.
Kuvvet Çiftinin Momenti: Kuvvet çifti, aralarında dik uzaklık d
olan, aynı büyüklükte ve zıt yöndeki paralel iki kuvvet olarak
tanımlanır. Bileşke kuvvet sıfırdır. Bu durumda kuvvet çiftinin
oluşturacağı etki belirli bir yönde dönme veya dönme eğilimi
üretmesidir. Kuvvet çifti ile üretilen momente kuvvet çiftinin
momenti denir.
Kuvvet çifti ile üretilen momente kuvvet çiftinin momenti
denir. Bu Moment uzaydaki herhangi bir keyfi O noktasına
göre belirlenen, iki kuvvetin momentlerinin toplamına
denktir.
M = rA (-F) rB (F) = ( rB - rA ) F
r ( rB - rA )
M = r F
M = Fd
Bileşke Kuvvet Çifti Momenti: Kuvvet çifti momentleri serbest
vektörler olduğundan cisim üzerine herhangi ibr noktaya
uygulanabilir ve vektörel olarak toplanabilirler
M R = M1 M 2
MR =
r F
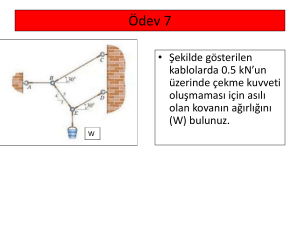
Örnek 6: Kiriş üzerine iki kuvvet çifti etkimektedir. F’nin
büyüklüğünü, bileşke kuvvet çifti momenti saatin tersi
yönde ve 450 N.m olacak şekilde belirleyiniz. Bileşke
kuvvet çifti momenti kiriş üzerinde nereye etkir?
MR M;
450 2000.6 F cos 30o 0.5
F 762 N
Bu bileşke kuvvet çifti momenti serbest vektördür. O kirişin herhangi bir noktasına etki edebilir.
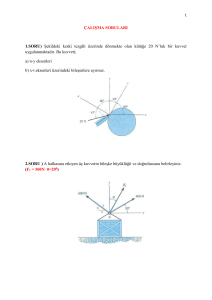
Örnek 7: Şekilde görülen beton bloklara etki eden kuvvet çiftlerinin oluşturacağı momenti
belirleyiniz.
M = -200 4 450 3 - 300 5
M 950 N m
Örnek 8: Boru üzerine etkiyen kuvvet çiftinin momentinin büyüklüğü
400 N.m olduğuna göre, her bir anahtara uygulanan düşey kuvvetin F
büyüklüğünü belirleyiniz.
i
j
M O rAB F k 0.35 0.2
0
0
M O 0.2 Fi 0.35 F j N m
MO
F
0.2 F 2 0.35F 2
k
0
F
400
400 2
992 N
0.22 0.352
Örnek 9: Yandaki şekilde görülen boru üzerine etkiyen iki kuvvet
çiftini, bileşke kuvvet çifti momenti ile değiştiriniz.
D(0, -0.225, 0.475)
M1 rDE FD
M1 0.225 j 0.300k 90 i
M1 27 j 20.25k
C(0, 0.225, 0.475)
M 2 rCD F
D(0, -0.225, 0.475)
rCD 0.450 j
FD 0.135 k
E(0, 0, 0.175)
rDE 0.225 j 0.300k
FD 90 i
M 2 60.75i
M O M1 M 2 60.75i 27 j 20.25k
Eşdeğer Kuvvet Sistemleri: Bir kuvvet bir cismi hem ötelemeye hem de döndürmeye
çalıştığından, kuvvet cisim üzerinde bir noktadan başka bir noktaya taşındığında, bu iki dış
etkinin aynı kalması gereklidir.
O noktası Kuvvetin Etki Çizgisi Üzerinde ise;
O noktası Kuvvetin Etki Çizgisi Üzerinde değil ise;
FR =
Kuvvet ve Kuvvet Çifti Sisteminin Bileşkesi
F
F
F
1
2
MRO = M C M O
M
=
M
M
=
M
M
;
C
C
O
1
2
M R O = M C M1 M 2
Örnek 10: Yandaki şekilde görülen kiriş üzerine etkiyen
kuvvet sistemini, O noktasında eşdeğer kuvvet ve moment
çiftine değiştirin.
Örnek 11: Aşağıda verilen yapı elemanı üzerinde şekilde görüldüğü
gibi M momentine ve F1, F2 kuvvetlerine maruzdur. Bu sistemi, O
tabanından etkiyen bir eşdeğer kuvvet ve kuvvet çifti momenti ile
değiştiriniz.
C(0, 0, 1) ;
B(-0.15, 0.1, 1)
rBC 0.15i 0.1 j
rBC
0.15i 0.1 j
45i 30 j
F2 F2
300
2
2
rBC
0.1803
0.15 0.1
F2 249.6i 166.4 j
F1 800k
FR = F F1 F2 800k 249.6i 166.4 j
FR 249.6i 166.4 j 800k
MRO =
M
M
C O
3
4
M 500 j 500k 400 j 300k
5
5
M R O = M rC F1 rB F2
M R O = 400 j 300k k 800k 0.15i 0.1 j k 249.6i 166.4 j
M R O = 166.4i 649.6 j 300k
Örnek 12: Makara üzerine geçen kayış, her biri 40 N
büyüklüğünde olan F1 ve F2 kuvvetlerine maruzdur. F1
kuvveti z ekseni doğrultusunda negatif yönde
etkimektedir. Bu kuvvetleri A’daki bir eşdeğer kuvvet
ve kuvvet çifti momentiyle değiştiriniz. Sonucu
Kartezyen vektör şeklinde ifade ediniz. =45o
F1 40k ; F2 40 cos 45o j 40 sin 45o k
F2 28.28 j 28.28k
FR F1 F2 F 40k 28.28 j 28.28k
FR 28.28 j 68.28k N
i
j
M RA 0.3 0.08
i
C(0, -0.08.sin45, 0.08.cos45)
rAC 0.3i 0.08 sin 45o j 0.08 cos 45o k
rAC 0.3i 0.05657 j 0.05657 k
j
0
28.28
rAB
B(0, 0.08, 0)
k
0 0.3 0.05657 0.05657
40
0
20.5 j 8.49k N m
0
M RA
k
rAC B
A(0.3, 0, 0)
M RA rAB F1 rAC F2
C
28.28
rAB 0.3i 0.08 j
Kuvvet ve Kuvvet Çifti İçin Ek İndirgeme
Cisim üzerindeki bütün kuvvet ve kuvvet çiftlerini, bizden istenen, bir O noktasına indirgenir. Böylece
O noktasında tek bir bileşke kuvvet FR = ∑F ve tek bir bileşke kuvvet çifti MR = ∑ MO elde edilir.
Daha sonra O noktasındaki bileşke kuvvet ve kuvvet çifti, aralarında olan d = MRo/Fr bağıntısıyla bir
P noktasına tek bir kuvvet olarak indirgenir.
Bir Noktadan Geçen Kuvvet Sistemleri
Düzlemsel Kuvvet Sistemleri
Paralel Kuvvet Sistemleri
Kuvvet ve Kuvvet Çifti Sistemlerinin Kuvvet Vidasına İndirgenmesi: Genel halde cisme
etkiyen kuvvet ve kuvvet çifti momenti sistemi, O noktasında birbirine dik olmayan tek bir FR
bileşke kuvvete ve MRo kuvvet çifti momentine indirgenir. MRo moment vektörü; Fr nin etki
çizgisine dik M┴ ve paralel M║ iki bileşene ayrılabilir.
MRo Kuvvet çiftinin dik bileşeni M┴ daha önceden gösterilen prensiplere göre P noktasına
taşınarak elemine edilir.
Diğer paralel bileşen M║, şiddeti ve doğrultusu değişmediği sürece, Fr
kaydırılabilir.
nin etki çizgisine
Böylece yukarıdaki şekilden de görülebileceği gibi; O noktasına indirgenmiş bir kuvvet sistemi, bir P
noktasında aynı doğrultuya sahip bir bileşke kuvvet ve bir kuvvet çiftiyle gösterilebiliyorsa bu tür
indirgenmiş sistemlere vidaya indirgeme denir.
Örnek 13: Büyük bir tankeri iskeleye yanaştırmak için dört
römorkör kullanılmaktadır. Her biri gösterilen yönde 5 kN ’luk
bir kuvvet uygulamaktadır. a) Baş direği O noktasında eşdeğer
kuvvet ve moment çiftine değiştirin, b) bu dört römorkörün
oluşturduğu etkinin aynısını oluşturacak daha güçlü tek bir
römorkörün omurganın hangi noktasından itmesi gerektiğini
bulunuz.
M R = 310.7k
FR
FR
FR = F F1 F2 F3 F4
2.5i 4.33 j 3i 4 j 5 j 3.54i 3.54 j
9.04i 9.79 j
9.79 j
FR
9.04i
FR 13,33 kN
9.79 j
9.04i
FR 13,33 kN
M R = r F 27i 15 j 2.5i 4.33 j
30i 21 j 3i 4 j 120i 21 j 5 j
90i 21 j 3.54i 3.54 j
M R = 310.7k
r xi 21 j
r FR M R
xi 21 j 9.04i 9.79 j 310.7k
r FR M R
x 9.79k 189.8k 310.7k
x 12.3 m
Basit Yayılı Yüklerin İndirgenmesi: Birçok durumda cismin çok büyük bir yüzey alanı,
rüzgarın, akışkanların neden olduğu veya sadece cismin yüzey aracılığıyla taşınan malzeme
ağırlığı gibi yayılı yüklere maruz kalır.
Bileşke Kuvvetin Büyüklüğü
Bileşke Kuvvetin Konumu: Bileşke kuvvetin konumunu belirlemek için O noktasına göre
moment dengesi yazılır. MR = ∑MO
x FR x dF x w(x) dx x dA
L
A
x
x w(x) dx x w(x) dx x dA
L
FR
L
w(x) dx
L
A
dA
A
Örnek 14: Şekilde görülen kiriş üzerine etki eden yayılı yükü,
tekil bileşke kuvvetin şiddetini ve konumunu bulunuz.
Örnek 15: Yükü, O noktasına etki eden eşdeğer
kuvvet ve kuvvet çifti momenti ile değiştiriniz.
FR Fy ;
FR 22.5 13.5 15
51kN 51 N
M RO M O ;
M RO 500 22.5 5 13.5 9 15 12
914 kN m 914 kN m
Örnek 15: Şekilde görülen kolon tepesinde 30 000 N bir kuvvet
uygulayan döşemeyi tutmaktadır. Kolon boyunca toprak
basıncının etkisi şekilde görüldüğü gibi yayılıdır. Bu yükü
eşdeğer bir bileşke kuvvet ile değiştirin ve kuvvetin kolon
boyunca A’dan itibaren hangi noktaya etkidiğini belirleyiniz.
2400 N
1800 N
FRx Fx ; FRx 2400 1800 4200 N
FRy Fy ;
FR
FRy 30 000 N
42002 30 0002
30 293 N
FR 30.3 kN
30 000
82o
4200
M A ; 4200 x 18001 24001.5
tan 1
M RA
x 2.286 m