14. ÜNİTE BASİT MAKİNALAR

14. ÜNİTE
BASİT MAKİNALAR
KONULAR
1. BASİT MAKİNALAR VE ÇEŞİTLERİ
2. Kaldıraçlar
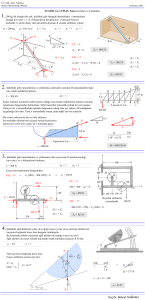
3. Makaralar
4. Sabit Makara
5. Hareketli Makaralar
6. Palangalar
7. Kasnaklar
8. Dişliler
9. Dönme Eksenleri Farklı Olan Dişliler
10. Dönme Eksenleri Aynı Olan Dişliler
11. Eğik Düzlem
12. Çıkrık
13. Vida
14. ÖZET
15. DEĞERLENDİRME SORULARI
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
14.1 BASİT MAKİNALAR VE ÇEŞİTLERİ
İnsanlar ilk günden itibaren işlerini kas kuvveti sayesinde görmüşler, kuv­
vetlerinin yetmediği zaman bunu nasıl yapacaklarını düşünmüşler, zekâları saye­
sinde bu zorlukları da yenmeyi başarmışlardır. Kas kuvvetiyle yapamadığı işi kolaylaştırarak yapan bir takım basit düzenekleri bulmuşlardır. Basit maki nal ar adını alan
bu düzenekler sayesinde bugünkü makinalar medeniyeti doğmuş ve görülen konforlar böylece elde edilmiştir.
Basit makinaların başlıcaları şunlardır
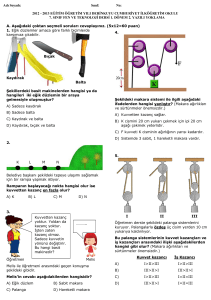
Kaldıraçlar
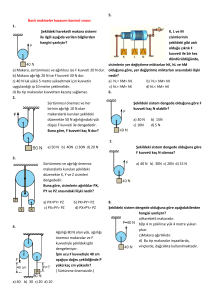
Palangalar
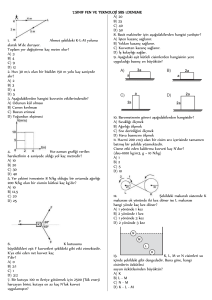
Kasnaklar
Dişliler
Eğik düzlemler
Çıkrıklar
Vidalar
Basit makinalar işi kolaylaştırırlar, fakat kazanç sağlamazlar. Bu kolay­lıktan dolayı biz işten de bir kazanç sağladığımızı zannederiz. Halbuki basit ma­kinalar bir işi;
başka bir işe yani ( kuvvet . yol ) hesabına çevirirler. Bunu ya­parken; kuvvet küçültürse yol artar yolu küçültürse kuvvet artar. Kuv­vetten kazanılanın yoldan kaybedildiği
anlaşılmış olur.
Basit Makine Çeşitleri
14.1.1 Kaldıraçlar
Bir destek üzerinde, sabit bir nokta etrafında dönebilen sis­temlere kaldıraç denir. Kaldıraçlar üç farklı şekilde incelenir;
Destek ortada ise
Şekil 14.1
235
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
F.x=P.y sonucu bulunur.
Ağırlıksız çubuk ve P yükü, F kuvveti ile şekildeki gibi den­gelendiğinde, x ve
y arasındaki ilişkiye göre, düzenekte kuvvetten ya da yoldan kazanç olup olmadığı
anlaşılır. Bu tip düzeneklere ör­nek olarak, pense, kerpeten, makas, tahterevalli, eşit
kollu verilebilir.
Yük ortada ise
Ağırlıksız Çubuk ve P yükü, F Kuvveti ile Şekildeki gibi dengelendiğinde,
x,y den büyük olduğu için F, P den küçüktür. Bu tip düzeneklerde kuvvetten
kazanç, yoldan ise kayıp vardır. Bunlara örnek olarak el arabası ve ceviz kıracağı verilebilir.
F.x=P.y sonucu bulunur.
Şekil 14.2
Kuvvet ortada ise
Ağırlıksız çubuk ve P yükü, F kuvveti ile şekildeki gibi den­gelendiğinde, x, y
den küçük olduğu için F, P den büyüktür bu tip düzeneklerde kuvvetten kayıp, yoldan ise kazanç vardır. Bunlara örnek olarak cımbız, maşa, zımba verilebilir.
F.x=P.y sonucu bulunur.
236
Şekil 14.3
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
ÖRNEK 1:
Ağırlığı 2P olan yük, P ağırlıklı ve eşit
bölmeli türdeş çubuk üzerindeki gibi şekildeki gibi F kuvvetiyle dengelendiğine göre, F
kuvvetinin büyüklüğü kaç P dir?
ÇÖZÜM:
Çubuğun dengede kalabilmesi için,
çubuğa etki eden kuvvetlerin desteğe göre
momentleri eşit olmalıdır.
2P . 1= P . 2 = F . 4
4P = 4F
F = P bulunur.
14.1.2 Makaralar
Makaralar bir eksen etrafında serbestçe dönebilen, etrafından ipin geçebilmesi için oluğu olan basit makinelerdir. İnşa­atlarda yüklerin taşınması, asansörlerin
yukarı yada aşağı hareket ettirilmesi gibi işlerde makaralar kullanılabilir. Makaralı
düzeneklerde cisimler üzerindeki işin daha kolay yapılması için uygulanan kuvvetin
yönü ve şiddeti değiştirilebilir. Makaralar kullanılış şekline göre ikiye ayrılır.
Resim 14.1: Makaralar
14.1.2.1 Sabit Makara
Merkezinden tavana asılan ve merkezi et­rafında dönebilen şekildeki sürtünmesiz makaraya sabit makara denir.
P yükü F kuvveti ile şekildeki gibi denge­lendiğinde, aynı ip üzerindeki gerilme
kuv­vetleri eşit olacağından, T = F dir. Yükün dengesinden,
F = P dir.
237
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Makara şekildeki gibi bir çubukla ta­vana asılıp farklı doğrultulardaki F,
kuvvetleri ile ayrı ayrı dengelen­diğinde,
F = = = P dir.
ve
Şekil 14.4: Sabit Makaralar
Sabit makaralarda
Kuvvetten ve yoldan kazanç yoktur.
İp ne kadar çekilirse, yükte o kadar yükselir.
Kuvvetin uygulama doğrultusunun önemi yoktur.
14.1.2.2 Hareketli Makaralar
Merkezine yük asılan ve etrafına sarılan ip üzerinde dönerek ilerleyen şekildeki maka­raya, hareketli makara denir.
Ağırlığı önemsiz makara ile P yükü, F kuvvetiyle şekildeki gibi dengede ise,
kuvvet dengesinden;
2F = P dir. Aynı zamanda F kuvvetinin değeri mo­ment dengesinden de bulunabilir. K noktasına göre moment alınırsa, F.2r = P.r
2F = P bulunur.
P yükü, ağırlığı G olan hareketli maka­rayla şekildeki gibi dengelenirse, kuvvet
dengesinden;
2F = G + P dir.
238
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Şekil 14.5: Hareketli Makaralar
Ağırlığı ve sürtünmesi önemsiz maka­raya bağlı olan P yükünü şekildeki gibi
h kadar yükseltmek için ipin ucunu F kuvvetiyle h kadar çekmek gerekir. Kuvvet
dengesinden,
2F = P
F=
dir. İş prensibinden, F.h = Rh
.
= P.h
= 2h olur.
Şekil 14.6: Hareketli Makaralar
Buna göre, yükün h kadar yükselmesi için, ipin ucu 2h kadar
çekilmelidir.
Şekil 14.7(a) deki gibi kurulan düzenekte makara ağırlığı önem­siz ise X makarasına etkiyen kuvvetlerin dengesinden,
239
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
2F = P
F=
olur.
Şekil 14.7(b) deki gibi kurulan düzenekte ise makaraların ağır­lığı P ise, Y makarasına etkiyen kuvvetlerin dengesinden,
3F = 2P
F=
olur.
Şekil 14.7(a)
Şekil 14.7(b)
14.1.3 Palangalar
Şekil 14.8
240
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Hareketli sabit makaraların Şekil 14.8 deki gibi aynı doğrultu üzerinde birleştirilmesi ile oluşan düzeneğe palanga denir. Bu sistemde kuvvetten kazanç, yoldan
kayıp vardır.
Ağırlıksız makaralarla kurulan şekildeki düzenekte, P yükü F kuvvetiyle den­
gede ise P, F ve h, arasındaki ilişki aşağıdaki gibi olur.
Kuvvet dengesinden,
4F = P F=
tür.
Yükün h kadar yükselmesi için ipin ucunun h kadar çekilmesi gerekir. İş prensibinden kuvvetin yaptığı iş yü­kün yaptığı işe eşit olmalıdır.
Buna göre,
P.h = F.
P.h =
.
= 4.h olur.
ÖRNEK 2:
Ağırlığı 80N olan yük, ağırlığı önemsiz makaralar
ve F kuvvetiyle şekildeki gibi dengeleniyor.
İpin ucu F kuvvetiyle 40 cm aşağı doğru çekildiğinde P yükü kaç cm yükselir? (Sürtünme önemsiz.)
ÇÖZÜM:
Aynı ipin her noktasında aynı gerilme kuvveti
olacağından iplerdeki gerilme kuvvetleri şekildeki
gibi olur. Basit maki­nelerde kuvvetten ne kadar kazanç varsa yoldan o kadar kayıp vardır.
Buna göre,
4F=80
F=20N olur.
Uygulanan kuvvet yükün dörtte biri kadar olduğundan yükün alacağı yol da kuvvetin aldığı yolun dörtte biri kadar olur. Bu nedenle P yükü 10 cm
yükselir.
241
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
14.1.4 Kasnaklar
Hareketi, birbirine kayışla aktaran düzenektir.
Şekil14.9(a,b): Kasnaklar
Şekil 14.9(a) de kayışla birbirine bağlı, r ve r yarıçaplı K ve L kas­naklarından
K ok yönünde dönerken, kayışın ilerleme yönü­ne bakılarak L nin de aynı yönde
döndüğü görülür. Kayış Şekil 14.9(b) deki gibi çapraz bağlanarak K ok yönünde
döndürül­düğünde, kayışın ilerleme yönüne bakılarak L nin zıt yönde döndüğü
görülür. K ve L kasnakları n ve n tur döndürül­düklerinde, kasnakların üzerinden
geçen kayış uzunlukları eşit olacağından,
Buna göre, tur yarıçapla ters orantılıdır.
Şekil14.10: Dişliler
242
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
14.1.5 Dişliler
4.1.5.1 Dönme Eksenleri Farklı Olan Dişliler
Dönme eksenleri farklı olan, hareketi birbirine dişleri ile aktaran şeklindeki
gibi düzenektir.
Şekil 14.11 de r, yarıçaplı dişli saat yönünde döndürülürse r yarıçaplı dişli saat
yönünün tersi yönde döner. Tur sayıları kasnaklarda olduğu gibi yarıçapla ters oran­
tılı yani
Dişli üzerindeki dişler özdeş olup, dişli sayısı yarıçapla doğru orantılıdır.
Şekil14.11: Dönme ekseni farklı olan dişliler
14.1.5.2 Dönme Eksenleri Aynı Olan Dişliler
Merkezinden perçinli olan dişlilerdir. Şekil 14.12 deki eş merkezli K ve L dişlileri
aynı merkez etrafında döndüklerinden dön­me yönleri ve tur sayıları aynıdır.
Şekil14.12: Dönme ekseni aynı olan dişliler
243
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
ÖRNEK 3:
2r, r ve 3r yarıçaplı K, L ve M
dişlileriyle kuru­lan şekildeki
düzenek­te K dişlisi ok yönünde 6 tur
döndürüldüğün­de M dişlisi hangi
yön­de kaç tur döner?
ÇÖZÜM:
Farklı eksenli dişlilerde tur sayısı
ile yarıçap ters oran­tılı olduğundan,
6.2r= n.3r
n= 4 tur.
Farklı eksenli dişlilerin dönme yönü zıt olduğundan K ile L, L ile de M zıt yönde döner. Buna göre, M dişlisi II
yönün­de 4 tur döner.
14.1.6 Eğik Düzlem
Ağır cisimleri yerden belli bir yüksekliğe, daha küçük kuvvetlerle çıkartmak
için kullanılan düzeneklerdir.
Şekil14.13: Eğik Düzlem
Bu düzeneklerde kuvvet; iş prensibine göre bulunur. Kuvve­tin yaptığı iş, yükün yaptığı işe eşittir. Şekildeki P yükü, düz­leme paralel F kuvveti ile sabit hızla çekildiğinde; F.s = P.h dır.
244
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
ÖRNEK 4:
Sürtünmenin ve makara ağırlığının önemsiz olduğu sistemde,
ve
ağırlıklı cisimler eğik düzlem üze­rinde şekildeki gibi denge­dedir.
İpte oluşan gerilme kuvvetinin büyüklüğü T olduğuna göre; , ve T arasındaki
ilişki nedir? (sin 30 =0,5)
ÇÖZÜM: Aynı ip üzerindeki gerilme kuvveti eşit olacağından ip gerilmesi her
noktada T dir. P yükünün dengesinden , =T olur.
İş prensibinden;
F.s=P.h 2T.2h
Buna göre;
P=4T dir.
> T=
olur.
14.1.7 Çıkrık
Şekil14.14: Çıkrık
245
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Bir kol ve buna bağlı çalışan silindirden oluşan düzenektir.
Kuyudan su çekmeye yarayan şekildeki çıkrıkta, R uzunlu­ğundaki çıkrık kolu
F kuvveti ile çevrildiğinde, her bir turda P yükünün bağlı olduğu ip silindire, silindirin çevre uzunluğu 2nr kadar sarılır ve kova da 2nr kadar yol alır.
Kovaya bağlı ipin sarılı olduğu silindirin merkez doğrusunun geçtiği O noktasına göre moment alınacak olursa, P.r= F.R olur.
Şekil14.15: Çıkrık
ÖRNEK 5:
K, L ve M cisimlerinin
şekildeki gibi asılı olduğu çıkrık
F kuvveti ile bir kez
döndürüldüğünde, cisimlerin
yer de­ğiştirme miktarları ,
ve
olduğuna göre, bunlar
arasındaki ilişki nedir ?
ÇÖZÜM:
Küçük ve büyük silindirler eş merkezli olduğundan ikisi de bir tur döner. L ve
M aynı silindire sarılı olduğu için yer değiştirme miktarları eşittir. ( = )
246
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
K ise küçük yarıçaplı silindire sarılı olduğu için yer değiştirme miktarı L ve M
nin kinden küçüktür.
Buna göre;
=
>
dir.
14.1.8 Vida
Genellikle tahta ya da metal cisimleri bir arada tutmaya yarayan ve üzerinde
burgulu dişleri olan çividir. Vidanın iki dişi arasındaki uzaklığa vida adımı denir ve a
ile gösterilir. Şekildeki vida bir tur döndürüldüğün de tahta zeminde bir vida adımı
a kadar ilerler. n tur döndürülen vidanın zeminde ilerleme miktarı h;
h = n.a bağıntısı ile bulunur.
L uzunluğundaki vida kolu F
kuvveti ile döndürülerek vida­nın
zeminde ilerlemesi sağlanırken,
zemin de vidanın ilerle­mesine
karşı direngen bir tepki kuvveti
(P) uygular. Kuvvetin vidayı ancak
döndürebildiği kabul edilirse, iş
prensibine gö­re, kuvvetin yaptığı
iş direngen kuvvetin yaptığı işe
eşit olur.
Buna göre;
F.2π.L = P.a dir.
Şekil14.16: Vida
ÖRNEK 6:
Vida adımları sırasıyla a ve 2a
olan K, L vidaları şekildeki gibidir.
Tahta bir zeminde, K vidası n tur döndürüldüğünde kadar ilerlediğine göre, L vidası 3n tur döndürüldüğünde kaç h ilerler?
ÇÖZÜM:
Vidanın zemininde ilerleme miktarı, h = n.a
formülü ile hesaplanır. Buna göre,
h= n.a formülü ile hesaplanır.
247
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Buna göre,
248
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
ÖZET
Basit Makinalar:
Kas kuvveti ile yapılamayan işleri kolaylaştıran basit düzeneklere denir. Basit
makinalar işi kolaylaştırırlar, fakat işten kazanç sağlamazlar.
Kaldıraç :
Genel olarak sabit bir eksen etrafında dönebilen dayanıklı katı cisimlere denir.
Kaldıraçlar bağıntısı
Bir kaldıraçta;
Kuvvet . Kuvvet Kolu = Yük . Yük kolu eşitliği vardır.
Buna kaldıraçlar bağıntısı denir.
Kaldıraç çeşitlen : Üç çeşit kaldıraç vardır:
Destek noktası ortada kaldıraç : Bu tip kaldıraçlarda dayanma noktası yük ile kuvvetin arasındadır, örnek : Makas.
Yük ortada kaldıraç : Bu tip kaldıraçlarda yük; dayanma noktası ile kuvvet
arasındadır, örnek : El arabası
Kuvvet ortada kaldıraç : Bu tip kaldıraçlarda kuvvet yük ile dayanma noktası
arasındadır, örnek : Maşa.
Makara :
Bir eksen etrafında dönen bir tekerlekçiktir. Etrafında ipin geçmesine ait bir oyuğu
vardır.
Makara çeşitleri : iki çeşit makara vardır.
Sabit makara : Makara dönme ekseninden sabit bir yere asılır, ip oyuk­tan geçirilir.
İpin bir ucuna yük, diğer ucuna yükün değerine eşit kuvvet uygu­lanır.
Yani;
G = F olur.
Sabit makara, kuvvetin doğrultusunu değiştirmeye imkân verdiği için bir kolaylık sağlar.
Haraketli makara : Yük, makaranın dönme eksenine asılır. İp makara oyuğundan geçer; bir sabit yere tesbit edilir, ipin diğer ucu ipi çekmede kulla­nılır.
Kuvvet; yükün yarısına eşittir.
F=
olur.
249
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Palangalar :
Sabit ve hareketli makaralardan meydana getirilen düzeneklere denir. Kuvvetin değeri; yükün makara sayısına bölümüne eşittir.
F=
( n Makara sayısı) olur.
Çıkrık:
Bir kol ve buna bağlı çalışan silindirden oluşan düzenektir
P.r= F.R olur.
Kasnaklar:
Hareketi, birbirine kayışla aktaran düzenektir.
formülü ile bulunur.
Dişliler:
Dönme eksenleri farklı olan dişliler:
Dönme eksenleri farklı olan, hareketi birbirine dişleri ile aktaran şeklindeki
gibi düzenektir.
Tur sayıları kasnaklarda olduğu gibi yarıçapla ters oran­tılı yani
formülü ile bulunur.
Dönme Eksenleri Aynı Olan Dişliler:
Merkezinden perçinli olan dişlilerdir. Dön­me yönleri ve tur sayıları aynıdır
Eğik Düzlem :
Bir yükün çıkarılacağı yüzeye eğik olarak konulan dayanıklı bir tahtanın meydana getirdiği düzeneğe denir.
Eğik düzlemde yükü tahta üzerinde hareket ettiren kuvvetin değeri;
F = G.
250
. formülü ile bulunur.
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
Vida:
Bir silindir üzerine bir eğik düzlemin sarılmasından elde edilen düzeneğe denir. Bir vida’ da yüke etki kuvvetin değeri;
G=F.
formülü ile bulunur.
251
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
DEĞERLENDİRME SORULARI
1)
şey
K noktasından menteşeli, ağırlıkları önemsiz ve eşit bölmeli kaldıraçlarda; dü,
ve
kuvvetleri, P ağırlıklı cisimleri şekillerdeki gibi dengelemiştir.
Buna göre, kuvvetlerden hangilerinin büyüklüğü, P den fazladır?
A) Yalnız
D)
ve
B) Yalnız C)
E)
ve
ve
2) Yarıçapları verilen şekildeki
dişli düzeneğinde
K, L, M, N dişlileri merkezlerinden
geçen eksen etrafında ser­
bestçe dönebilmektedir. X dişlisi
döndürüldüğünde, K, L, M, N
için;
I. X dişlisine göre zıt yönde
dönerler.
II. Tur sayısı en az olan L
dişlisidir.
III. X dişlisi 5 tur döndürülürse,
N dişlisi 4 tur döner.
yargılarından hangileri doğrudur?
A) Yalnız I
252
D) II ve III
B) Yalnız II
E) I, II ve III
C) I ve II
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
3)
ve
yükleri şekildeki düze­nekte dengededir.
Buna göre,
yükü ok yönün­de h kadar çekildiğinde
kaç h yer değiştirir?
B)
A)
C)1
D) 2
yükü
E) 4
4) Özdeş K ve L cisimleri ile ağırlığı ve sürtünmesi önemsiz makaralardan oluşan
sistem şekildeki gibi dengede tutuluyor.
A)
Hareketsiz
Hareketsiz
B)
AşağıAşağı
C)
YukarıAşağı
D)
YukarıYukarı
E)
AşağıYukarı
5) Sürtünmesiz eğik düzlemde P ağırlıklı
cisimler şekildeki gibi dengededir.
Gösterilen ipteki gerilme kuvveti
T olduğuna göre;
oranı
kaçtır?(sürtünmeler önemsiz. )
A)
B) 1
D) 2
C)
E) 3
253
2. SINIF ELEKTRİK TESİSATÇILIĞI
TEMEL MATEMATİK VE FİZİK
6) Adımı a, vida kolunun uzunluğu b olan Şekil-I deki vida ile Şekil-ll deki r yarıçaplı
silindirle kurulan çıkrık düzeneğinde; kuvvet kazançlarını artırabil­mek için a, b, R
ve r büyüklüklerinden hangilerini artırmak gerekir?
A)
a
r
B)
b
R
C)
a
R
D)
b
r
E)
F
F
254