Document

AĞIRLIK MERKEZİ
Kütle; skaler bir büyüklük olup, madde miktarıyla
ilgili bir özelliktir. Ağırlık ise yerin cisme uyguladığı
çekim kuvvetidir.
Birim kütleye etki eden yer çekim kuvvetine yerin

çekim alanı denir ve “ g ” ile gösterilir. Buna göre
cismin ağırlığı,


G  m.g
Düzgün Geometrik Yapılı Bazı Cisimlerin Ağırlık
Merkezi
‘dir.
Bir cismin ağırlık merkezi, cismin ağırlık
vektörünün başlangıç noktası olarak tanımlanır.

1) Türdeş çubuğun ağırlık merkezi, çubuğun tam
orta noktasındadır. (Uzunluk)
Bir cismin ağırlığı birim kütlelerin ağırlıkları
toplamına eşittir.
2) Türdeş olan, kare, dikdörtgen ve paralel kenar
şeklindeki levhaların ağırlık merkezi köşegenlerin
kesim noktasıdır. (Alan)

Cisim ağırlık merkezinden iple
asıldığında düşey dengede kalır.
tavana
3) Türdeş üçgen levhanın ağırlık merkezi,
kenarortayların kesim noktası olan O noktasıdır. Bu
nokta kenardan 1 birim, köşelerden 2 birim
uzaklıktadır. Üçgen levha eşkenar üçgen şeklinde
olursa, kenarortayların hepsi eşit olur.

Nasıl asarsak asalım ipin uzantısı ağırlık
merkezinden geçer. Bir cisim ağırlık
merkezinden asılırsa cisim yatay dengede kalır.

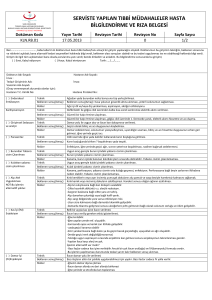
Bir cismin dengede kalabilmesi için ağırlık
merkezinden indirilen düşey doğrultunun
taban düzlemi içerisinde kalması gerekir.
1
4) Türdeş küre, daire ve çemberin ağırlık merkezi,
cisimlerin geometrik merkezleridir. (Hacim)
X KM 
G1 .x1  G2 .x2  G3 .x3
G1  G2  G3
X KM 
m1 .x1 .g  m2 .x2 .g  m3 .x3 .g
m1 .g  m2 .g  m3 .g
X KM 
m1 .x1  m2 .x2  m3 .x3
m1  m2  m3
Sonra ağırlık merkezinin y eksenini kestiği nokta
aşağıdaki yöntemle hesaplanır.
5) Türdeş silindir, dikdörtgen prizma ve küpün
ağırlık merkezi, üst ve alt taban merkezlerini
birleştiren doğrunun tam orta noktasındadır.
(Hacim)
YKM 
G1 . y1  G2 . y 2  G3 . y 3
G1  G2  G3
YKM 
m1 . y1 .g  m2 . y 2 .g  m3 . y 3 .g
m1 .g  m2 .g  m3 .g
YKM 
Koordinat Sisteminde Ağırlık Merkezinin
Bulunması
m1 . y1  m2 . y 2  m3 . y3
m1  m2  m3
Bu iki değer bize ağırlık merkezinin koordinatlarını
verir.
AKM = ( XKM , YKM )
Özellikler
1) Ağırlık merkezi problemleri “paralel kuvvet”
yöntemiyle bulunur.
2) Homojen bir telin ucundan “a” kadarlık parçası
kesilerek atılırsa, ağırlık merkezi,
Noktasal kütlelerden oluşan bir sistemin ağırlık
(Kütle) merkezini bulmak için önce koordinat
sistemi içine yerleştirilir.
∆x = a / 2
kadar yer değiştirir.
Önce ağırlık merkezi vektörünün x eksenini kestiği
nokta aşağıdaki yöntemle hesaplanır.
2
3) Homojen bir çubuğun bir ucundan “a” kadarı
kendi üzerine katlanırsa, ağırlık merkezi
katlanmayan tarafa doğru
∆x = a ² / ℓ
kadar yer değiştirir.
4) Bir cismin 1 / a ‘lık kısmı çıkarılıp başka bir
yere
yapıştırılırsa
ağırlık
merkezi
x
doğrultusuna paralel olarak x / a kadar kayar.
G₁ =a.b

5) Bir cismin ağırlığı, uygun şartlarda kütle,
uzunluk, alan, hacim ve yoğunlukla doğru
orantılıdır.
G₂ = π.r ²
Bir levhadan herhangi bir parça kesilerek
çıkarılırsa;
çıkarılan
parçanın
ağırlık
merkezinden yukarıya doğru ağırlığına eşit bir
kuvvetin uygulandığını kabul ederek işlem
yapar, yeni ağırlık merkezini buluruz.
m=d.V
Bir sistemin ağırlık merkezini bulmak için:
1) Cismin ağırlık merkezi bilinen geometrik
parçaya ayrılır.
2) Her parçanın ağırlık merkezi ve ağırlık
kuvvetleri paralel kuvvetler olarak çizilir.
G₁=a.b
3) Bu paralel kuvvetler arasındaki uzaklıklar
hesaplanır ve moment alınarak bileşkenin
uygulama noktası bulunur. Bu sistemin ağırlık
merkezini verir.

Bir levhaya herhangi bir parça eklenirse
eklenen parçanın ağırlık merkezinden aşağıya
doğru ağırlığına eşit bir kuvvetin uygulandığını
kabul ederek işlem yapar ve yeni ağırlık
merkezini buluruz.
3
G₂= πr ²