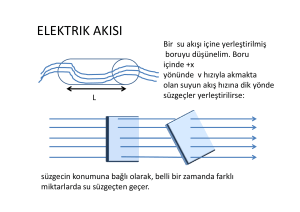
Statik Manyetik
Alan
Noktasal Yüke Etki eden Manyetik Kuvvet
Akım Elemanına Etki Eden Manyetik Kuvvet
Biot-Savart Kanunu
Statik Manyetik Alan
• Statik manyetik alan, sabit akımdan veya bir sürekli
mıknatıstan kaynaklanabilir
• Bu bölümde sabit akımların oluşturduğu manyetik alanlar
incelenecektir.
Statik Elektrik Alan
E
D
Elektrik Alan
Vektörü [V/m]
Elektrik Akı Yoğunluğu
(Deplasman Vektörü)
[C/𝑚2 ]
Eğer ortam homojen ve izotropikse
(yönden bağımsız) ise elektrik alan
şiddeti ve deplasman vektörü arasında
aşağıdaki ilişki vardır
D .E
Statik Manyetik Alan
H
B
Manyetik Alan Şiddeti
[A/m]
Manyetik akı yoğunluğu
[Wb/𝑚2 ] ,[Tesla] veya [Gauss]
1Tesla= 104 Gauss
Eğer ortam homojen ve izotropik
(yönden bağımsız) ise manyetik alan
şiddeti ve manyetik akı yoğunluğu
vektörü arasında aşağıdaki ilişki
vardır
𝐵 = 𝜇. 𝐻
Noktasal Yüke Etkiyen Manyetik
Kuvvet
• Noktasal q yüküne B manyetik alanı içinde etki
eden manyetik kuvvet:
FB q[v B]
• Manyetik kuvvetin yönü sağ el kuralı ile bulunur.
z
Fm qv B
v vx iˆ vy ĵ
B Bx iˆ By ĵ
iˆ
F vx
Bx
iˆ
F vx
Bx
ĵ
vy
By
ĵ
vy
By
k̂
vy
0
By
0
0
v
ˆi 0 vx ĵ x
0 B
B
0
x
x
k̂
0 (vx By Bx vy )k̂
0
vy
k̂
B
y
y
j
k
i
x
Pozitif yük, Manyetik Alan içerisinde Hareket Ediyor.
B, sayfadan içeri doğru
F v B
Fm qv B = qvBsin90o
Kuvvetin yönü , sağ el kuralı ile
bulunur
Yüke etki eden
kuvvet:
Dairesel yolun
yarıçapı:
Açısal Hız:
Hareketin
periyodu:
mv 2
FB qvB
r
mv
r
qB
v qB
r m
2r 2 2m
T
v
qB
Örnek: Bir proton, 0.4 Tesla’lık manyetik akı yoğunluğu içerisinde 21 cm yarıçaplı yörüngede
hareket etmektedir. Protonun hızını ve frekansını bulunuz.
1
x
v x
x
x
qBr
m
1.6 10 19 C (0.4T ) 0.21m
v
1.67 10 27 kg
x
r
x
v
1.6 (0.4) 0.21
v
10 8
1.67
x
x
v 8.110 6
2
f
m
s
8.1 10 6
m
s
qB
2m
1.6 10 19 C (0.4T )
f
(2 ) 1.67 10 27 kg
1.6 (0.4)
f
10 8 Hz 6.1 10 6 Hz
(6.28) 1.67
f 6.1 10 6 Hz
m
s
Akım Elemanı Üzerine Etki Eden Kuvvet
• Manyetik alan içerisinde hareket etmekte olan yüklü parçacığa etki
eden kuvvet bağıntısı iletkenlerdeki akım için kullanışlı olmadığından;
akım elemanı üzerine etki eden kuvvet bağıntısı çıkartılacaktır.
𝑑𝑞
𝐼=
𝑑𝑡
olduğu hatırlanıp ;
𝑑ℓ= 𝑣 . 𝑑𝑡
𝐼=
alınabilir. dt çekilip
yukarıdaki denklemde
yazılırsa;
𝑑𝑞
𝑑ℓ
.𝑣
elde edilir.
Diğer taraftan, akımı akım yoğunluğu
cinsinden aşağıdaki gibi yazabiliriz.
𝐼 = 𝐽. 𝑑𝑆
𝐽=
𝐼
𝑑𝑞
=
.𝑣
𝑑𝑆 𝑑ℓ.𝑑𝑆
= 𝜌. 𝑣
v hızı ile hareket eden dq yük grubuna etki eden kuvvet aşağıdaki gibi bulunabilir.
𝑑𝐹=dq.𝑣 × 𝐵
𝑑𝑞=𝜌. 𝑑ℓ. 𝑑𝑆
𝑑𝐹= 𝑑ℓ. 𝑑𝑆. 𝜌 . 𝑣 × 𝐵
𝑑𝑣
𝑑𝐹= 𝐽 × 𝐵𝑑𝑣
𝐽
𝐹=
𝐽 × 𝐵𝑑𝑣
𝑣
Üzerinden I şiddetinde akım geçmekte olan uzun bir tel için;
𝑑𝐹 = 𝐼. 𝑑ℓ × 𝐵
𝑑𝐹= 𝑑ℓ. 𝑑𝑆.𝐽 × 𝐵
Telin tümüne etki edecek
olan manyetik kuvvet;
𝐼
𝐹=
𝑡𝑒𝑙
(𝐼. 𝑑𝑙 𝑥 𝐵 )=I
𝑡𝑒𝑙
(𝑑𝑙 𝑥𝐵)
Amper’in Kuvvet Kanunu
Üzerinden akım geçen bir iletkenin çevresinde bir manyetik alan meydana gelir. Bu
alana başka bir iletken sokulursa bunlar karşılıklı olarak birbirine etki ederler. Bu olay
Amper tarafından deneysel olarak ispatlanmış ve şekildeki örnek için;
𝐼2 . 𝑑ℓ2 × (𝐼1 . 𝑑ℓ1 × 𝑅21 )
𝐹21 = 𝑘.
𝑐1 𝑐2
k sabittir.
𝜇0
𝑘=
4𝜋
𝑅21 3
eşitliği ile verilmiştir.
𝜀0 =
1
36𝜋109
[F/m]
𝜇 0 = 4𝜋10−7 [𝐻/𝑚]
Boşluğun dielektrik katsayısı
Boşluğun manyetik geçirgenlik katsayısı
Işık Hızı
𝑐=
1
𝜇0 .𝜀0
=
1
4𝜋10−7 .
1
36𝜋109
= 3. 108 [m/sn]
Üzerinden Akım Geçen İletkenin Manyetik
Alanı
Manyetik alan içindeki, üzerindeki I akımı geçen tele etkiyen kuvvet aşağıdaki gibi
tanımlanmıştı.
𝑑𝐹 = 𝐼. 𝑑ℓ × 𝐵
İki iletkenin Amper’in kuvvet kanunu uyarınca uyguladıkları kuvvet ise aşağıdaki
gibi yazılabilir.
𝑑𝐹21
𝜇0 𝐼2 . 𝑑ℓ2 × (𝐼1 . 𝑑ℓ1 × 𝑅21 )
=
.
4𝜋
𝑅21 3
İki eşitlik karşılaştırıldığında;
𝜇0 𝐼2 . 𝑑ℓ2 × (𝐼1 . 𝑑ℓ1 × 𝑅21 )
𝐼. 𝑑ℓ2 × 𝑑𝐵1 = .
4𝜋
𝑅21 3
yazılabilir.
Biot-Savart Kanunu
𝜇0 𝐼2 . 𝑑ℓ2 × (𝐼1 . 𝑑ℓ1 × 𝑅21 )
𝐼. 𝑑ℓ2 × 𝑑𝐵1 = .
4𝜋
𝑅21 3
Herhandi bir 𝐼. 𝑑ℓ akım elemanının 𝑅 kadar uzağında meydana getireceği manyetik
akı yoğunluğu Biot-Savart kanunu olarak bilinen aşağıdaki denklemle
hesaplanabilir;
𝑑𝐵 =
𝜇0 𝐼.𝑑ℓ×𝑅
.
4𝜋
𝑅3
=
𝚤𝑅 : R doğrultusundaki birim vektördür
𝜇0 (𝐼.𝑑ℓ×𝚤𝑅 )
.
4𝜋
𝑅2
Akım Elemanının Manyetik Alanı
Üzerinden akım geçen bir
telin çevresinde meydana
getireceği manyetik akı
yoğunluğu vektörü aşağıdaki
formül ile hesaplanır.
P
𝒅ℓ
𝑹
𝚤𝑹
I
𝜇0
𝐵=
.
4𝜋
𝑐
(𝐼. 𝑑ℓ × 𝚤𝑅 )
𝑅2
Örnek
•
Z ekseni boyunca uzanan bir tel üzerinden I şiddetinde akım akmaktadır. z=-a
ve z=+a arasında uzanan iletken parçasının meydana getireceği manyetik akı
yoğunluğu vektörünü bulunuz.
𝑃(𝑟, Φ, 𝑧)
z
a
𝑰. 𝒅𝒛′ . 𝚤𝒛
𝛼2
𝛼
𝚤𝑹
z
z’
y
𝛼1
x
-a
I
r
𝑑𝐵 =
𝜇0 (𝐼.𝑑ℓ×𝚤𝑅 )
.
4𝜋
𝑅2
𝑎
𝐵=
𝑧 ′ =−𝑎
𝑧 − 𝑧 ′ = 𝑟. 𝑐𝑜𝑡𝛼
𝐵=
=
𝜇0
𝑑𝐵 =
4𝜋
𝜇0
𝐼.𝑑𝑧 ′ .𝑠𝑖𝑛𝛼
.
.𝚤
4𝜋 [𝑟 2 + 𝑧−𝑧 ′ 2 ] 𝜙
𝑎
−𝑎
𝐼. 𝑑𝑧 ′ . 𝑠𝑖𝑛𝛼
. 𝚤𝜙
2
′
2
[𝑟 + 𝑧 − 𝑧 ]
dönüşümü yapılırsa;
𝜇0. 𝐼 𝑎
𝜇0. 𝐼
𝑠𝑖𝑛𝛼. 𝑑𝛼. 𝚤𝜙 = (𝑐𝑜𝑠𝛼1
4𝜋𝑟 𝑧 ′ =−𝑎
4𝜋𝑟
𝐵=
𝜇0. 𝐼
(𝑐𝑜𝑠𝛼1
4𝜋𝑟
− 𝑐𝑜𝑠𝛼2 ). 𝚤𝜙
− 𝑐𝑜𝑠𝛼2 ). 𝚤𝜙
𝐵=
𝜇0. 𝐼
𝚤𝜙
2𝜋𝑟
Örnek
Üzerinden I büyüklüğünde akım geçmekte olan a yarıçaplı iletken halkanın ekseni
üzerindeki noktalar için manyetik akı yoğunluğu vektörünü bulunuz.
𝑑𝐵 =
𝑑ℓ
𝜇0 (𝐼. 𝑑ℓ × 𝚤𝑅 )
.
4𝜋
𝑟2
𝑑𝐵𝑥 = 𝑑𝐵. 𝑐𝑜𝑠
𝑑𝐵. 𝑐𝑜𝑠 =
𝐵𝑥 =
𝜇0 . 𝐼. 𝑅
4𝜋(𝑥 2 +𝑅2 )3/2
𝜇0 . 𝐼. 𝑅2
𝐵𝑥 =
2. (𝑥 2 +𝑅2 )3/2
x=0 için
𝜇0 . 𝐼
𝐵=
2. 𝑅
𝜇0 . 𝐼
4𝜋
𝐵𝑥 =
𝑑ℓ. 𝑐𝑜𝑠𝜃
𝑥 2 + 𝑅2
𝑑ℓ
2𝜋𝑅
• Kapalı, düzlemsel bir akım devresinin sınırladığı yüzeyin alanı
S ve bu devreden geçen akım şiddeti I ise, S.I çarpanına akım
devresinin manyetik momenti denir.
𝑚 = 𝑆. 𝐼. 𝚤𝑛
Manyetik moment tanımını, bir önceki örnekte bulduğumuz
eşitlikte kullanabiliriz.
𝜇0 . 𝐼
𝐵=
2. 𝑅
. 𝐼. 𝜋. 𝑅2
𝜇0
𝐵=
2. 𝜋. 𝑅3
𝜇0 . 𝑚
𝐵=
2. 𝜋. 𝑅3
S
Örnek
Üzerinden I büyüklüğünde akım geçmekte olan telin O noktasında oluşturacağı
manyetik akı yoğunluğunu bulunuz.
𝜇0 (𝐼. 𝑑𝑙 × 𝚤𝑅 )
𝑑𝐵 =
.
4𝜋
𝑅2
𝑑𝑙
𝚤𝑟
𝜇0 . 𝐼 𝑑𝑙
𝑑𝐵 =
. 2
4𝜋 𝑅
𝜇0 . 𝐼
𝐵=
4𝜋𝑅2
0
𝜇0 . 𝐼
𝑑𝑙=
4𝜋𝑅2
0
𝜇0 . 𝐼.
𝑅. 𝑑=
4𝜋𝑅