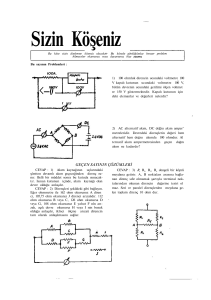
Temel Devre Elemanlarının
Alternatif Gerilim Etkisi Altındaki
Davranışları
Direnç (R)
• Alternatif gerilimin etkisi altındaki direnç, Ohm kanunun bilinen
ifadesini korur.
Denklemlerden elde edilen sonuç gösterir ki bir direnç üzerine düşen
gerilim ile akım arasında faz farkı yoktur. Sadece genlik Ohm kanuna
uygun şekilde değişir.
Bobin (L) (Endüktans)
• Alternatif gerilimin etkisi altındaki bobinler, dirençten farklı olarak
akımındeğişimine karşı bir direnç etkisi gösterirler. Üzerlerine düşen
gerilim (bobinin iki ucu arasında ölçülen) Lenz Kanuna uygun olarak
bulunur.
• Bu ifadeyi alternatif akımı göz önüne alarak incelersek bir bobinin
üzerinde düşen gerilim ile ilişkisini tahmin edebiliriz.
• Bu sonuç bize gösterir ki bobinin üzerine düşen gerilim ile akım
arasında 90 derece faz farkı vardır. Gerilim akımın 90 derece
önündedir.
• Bu faz farkının doğal sonucu olarak elektriksel güç negatif/pozitif
olmaktadır. Negatif güç ifadesi bobinin devreye güç aktardığını
göstermektedir.
• Bobinlerin “direnci” zamana alternatif gerilimin frekansına bağlı
olarak değişmektedir. Bunun için buna reaktans (Endüktif reaktans XL)
denmektedir.
• Reaktans ifadesi kullanılarak Ohm kanunu alternatif akım devrelerine
kolayca uygulanabilir. Bu durumda sadece skaler sayılar yerine
karmaşık sayılar ile hesap yapmak gerekecektir.
Direnç değeri:
Bobinin endüktif reaktansı
Bu iki etkinin bir arada ifadesine empedans denir.
Genel anlamda alternatif gerilim devrelerinde direnç etkisinin karşılığı
olarak kullanılır. Yukarıda da verildiği üzere Ohm kanununda direnç
ifadesinin yerine kullanılır.
Paralel devre
Kondansatör (Kapasitans)
• Alternatif gerilimin etkisi altındaki kondansatörler, üzerlerine düşen
gerilimin değişmine bağlı tepki verirler, eğer kondansatör uçlarına,
üzerinde mevcut olan gerilimden daha düşük bir gerilim uygulanırsa,
kondansatör devreye akım sağlar, (deşarj olur), eğer kondansatör
uçlarına, üzerinde mevcut olan gerilimden daha büyük bir gerilim
uygulanırsa, kondansatör devreden akım çeker (Şarj olur).
• Bu bilgi ışığında kondansatörün akımı ve üzerindeki gerilim arasındaki
ilşki aşağıdaki gibi verilir.
• Bu sonuç bize gösterir ki kondansatörün üzerine düşen gerilim
ile akım arasında 90 derece faz farkı vardır.
• Akım gerilimin 90 derece önündedir.
• Bu faz farkının doğal sonucu olarak elektriksel güç negatifpozitif olmaktadır.
• Negatif güç ifadesi kondansatörün devreye güç aktardığını
(deşarjolduğunu) göstermektedir.
• Kondansatörlerin “direnci” zamana, alternatif gerilimin
frekansına bağlı olarak değişmektedir.
• Kondansatörler gerlimdeki değişimler (frekans) arttıkça daha
fazla akım geçirirler. Bu duruma kapasitans(kapasitif reaktans
Xc) denmektedir.
• kondansatörlerin alternatif gerilim etkisi altındaki davranışını
matematiksel olarak inceleyelim. Kapasitif reaktans denklemi ve Ohm
yasasının alternatif gerilime uygulamasından yararlanarak devreden
akan akım bulunur.
• Devreden geçen akım ise Ohm kanunun alternatif devreye
uyarlanması ifadesinden bulunur. Burada kritik nokta gerilim
kaynağının fazıdır. Bu tip devre analizlerinde bu değer hep 0 kabul
edilir.
Paralel direnç – kondansatör devresi
Direnç, Reaktans ve Empedans Kavramları
Bu noktaya kadar yapılan devre analizlerinde akıma karşı koyma etkisini 3 farklı
şekilde adlandırdık.
• Direnç; ifadesi iletken içerisindeki elektron hareketinin karşılaştığı
sürtünmeyi ifade eder. Sembolü “R”, birimi “Ω” Ohm’dur. Direnç etkisi akım
ile gerilim arasında bir faz farkı oluşturmaz.
• Reaktans; ifadesi elektronların ataletini (eylemsizliğini) belirtir. Bu etki
gerilim ve akım değerlerinde değişim olduğunda, başka bir deyişle elektrik
alan ve manyetik alan oluşumu söz konusu olduğunda ortaya çıkar.
Kondansatör ve bobin bu etkinin en belirgin olduğu devre elemanlarıdır.
• Reaktans etkisi olduğunda akım ile gerilim arasında 90 derece faz farkı
oluşur. Eğer söz konusu elaman bobin ise gerilim akımdan 90 derece ileri
fazdadır, eğer kondansatör ise akım gerilimden 90 dereceileri fazdadır.
• Empedans ifadesi, bir elektrik devresinde akıma gösterilen
zorluğun yani elektron hareketine karşı koyma etkisinin genel
ifadesidir. Devredeki tüm elemanların direnç ve reaktans
etkilerinin toplamını ifade eder.
• Empedans doğru akım devresindeki direnç etkisinin alternatif
akım devresindeki tam karşılığıdır.
• Buna göre değiştirilmiş Ohm kanunu ifadesi aşağıda verildiği
gibidir. Burada dikkat edilmesi gereken nokta tüm büyüklüklerin
karmaşık sayı olduğudur.
• Ohm kanunu gibi diğer devre analizi kanunları, Kirrchhoff gerilim
ve akım yasaları, şebeke teoremleri de ifadeler karmaşık sayı
olmak koşul ile alternatif akım devrelerinde de aynen geçerlidir.
• Alternatif akım devrelerinde temel fark güç hesabında ortaya
çıkmaktadır.
Seri RLC devreleri
Paralel RLC
Alternatif Akım Devresinde Güç Hesabı
• Yukarıda verilen devre analizlerinde alternatif akım devrelerinde
akım ile gerilim arasında bir faz farkı olduğunu gördük. Bunun
sebebinin karmaşık sayı ile ifade edilen empedans olduğu belirtildi.
• Alternatif akım devresinde güç hesabı yapılırken yine empedans
ifadesi esas alınarak üç farklı tanım yapılır. Bunlar sırasıyladevredeki
direnç etkisine istinaden bulunan gerçek (yada rezistif) güç: