SAYISAL İNTEGRAL
c ϵ R olmak üzere F(x) fonksiyonunun türevi f(x) ise ( F’(x) = f(x) );
f x dx
F x c eşitliğindeki “F(x)+c” ifadesine, f(x) fonksiyonunun belirsiz integrali
denir.
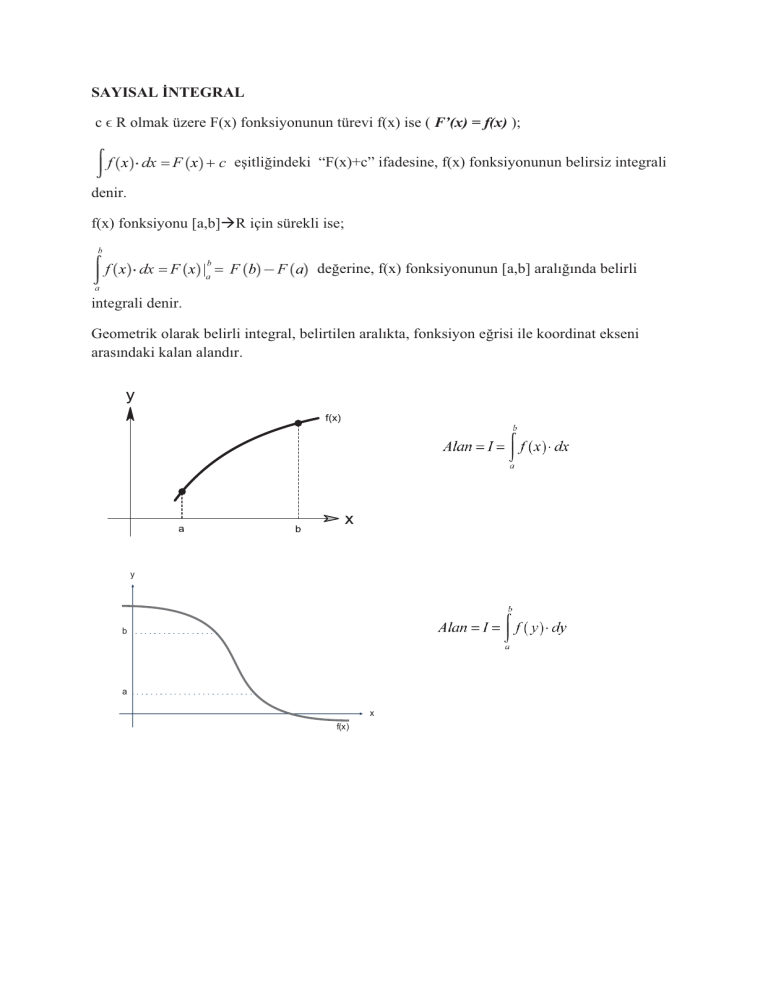
f(x) fonksiyonu [a,b]ÆR için sürekli ise;
b
f x dx
b
F x |a
F b
F a değerine, f(x) fonksiyonunun [a,b] aralığında belirli
a
integrali denir.
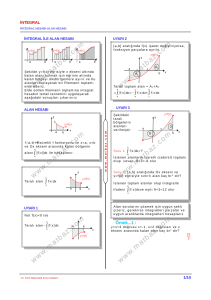
Geometrik olarak belirli integral, belirtilen aralıkta, fonksiyon eğrisi ile koordinat ekseni
arasındaki kalan alandır.
y
b
a
x
f(x)
İntegrali kolaylıkla hesaplanabilen eğriler;
Diktörtgen alanı;
Yamuk alanı (f(x)=x/2);
İntegral Uygulamaları ;
1. Eğri altında kalan alanı bulmak,
2. İki eğri arasında kalan alanı bulmak,
y
f(x)
g(x)
a
b
x
3. Bir eğrinin x veya y ekseni etrafında 360o döndürülmesi ile oluşan kapalı bölgenin hacmini
bulmak,
y
y
f(x)
b
f(x)
a
a
x
Elektrik Mühendisliğinde kullanılan bazı integral uygulamaları;
1. Ortalama değer hesabı;
y
fort
T
2. Etkin değer hesabı;
f
2
et
1
T
T
f
2
x dx
0
3. Fourier serilerinin hesabında.
x
b
x
Yüksek dereceli polinomlarda veya karmaşık fonksiyonların belirli integrallerinin hesabında,
eğri ile koordinat ekseni arasında kalan alanın hesabı zordur. Bu alanlar bilinen geometrik
şekillerin alanları kullanılarak, yaklaşık olarak hesaplanabilir. Yani eğri ile koordinat ekseni
arasında kalan alan daha küçük ve bilinen geometrik şekillere bölünerek elde edilen alanlar
toplanarak hesapalanabilir.
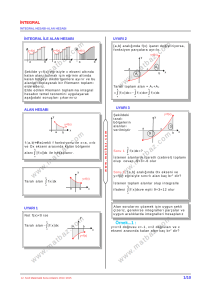
Sayısal Yöntemler;
1. Dikdörtgenler yöntemi
İntegrali bulunacak eğri ilgili aralıkta küçük dikdörtgenlere bölünür, bu dikdörtgenlerin
alanları toplanarak yaklaşık sonuç bulunur.
1.a) Sol toplamlar
[a,b] aralığı n parçaya bölünür. Adım h
b
a
n
‘dir. i=0,1,2,..,n-1 için xi+1=xi+h
y
f(x)
f(x 2)
f(x 1)
f(x 0)
a=x 0
I3
I2
I1
x1
x
b=x 3
x2
1.b) Sağ toplamlar
[a,b] aralığı n parçaya bölünür. Adım h
b
a
n
‘dir. i=1,2,..,n için xi+1=xi+h
y
f(x)
f(x 3)
f(x 2)
I3
f(x 1)
I2
I1
a=x 0
x1
x2
b=x 3
x
1.c) Orta toplamlar
[a,b] aralığı n parçaya bölünür. Adım h
b
a
n
‘dir. i=0,1,..,n-1 için xi+1=xi+h
y
f(x)
f(x 2 +h/2)
f(x 1 +h/2)
f(x 0 +h/2)
I1
a=x 0
x1
x 0 +h/2
I3
I2
b=x 3
x2
x 1 +h/2
x 2 +h/2
x
Örnek :
7
3 x 2 dx integralini dikdörtgenler yöntemini kullanarak bulunuz. (n=3,5,10)
1
7
Analitik
Alan
3 x 2 dx
I
1
n=3 için h
b
a
n
Sol toplamlar
Sağ toplamlar
Orta Toplamlar
7
1
3
2
7
x 3 |1
7
3
1
342
MATLAB Kodları
%sol
clc;
%integral sinirlari
a=1;
b=7;
n=input ('Parca =');
h=(b-a)/n;
fprintf('Adim = %.3f \n', h);
toplam=0;
x=1;
for i=1:n
y=3*x^2;
fprintf('%d. alan=%.3f\n', i,y);
x=a+i*h;
toplam=toplam+h*y;
end;
fprintf('yaklasik integral = %.3f \n', toplam);
%sag
clc;
%integral sinirlari
a=1;
b=7;
n=input ('Parca =');
h=(b-a)/n;
fprintf('Adim = %.3f \n', h);
x=1;
toplam=0;
for i=1:n
x=a+i*h;
y=3*x^2;
fprintf('%d. alan=%.3f\n', i,y);
toplam=toplam+h*y;
end;
fprintf('yaklasik integral = %.3f \n', toplam);
%orta
clc;
%integral sinirlari
a=1;
b=7;
n=input ('Parca =');
h=(b-a)/n;
fprintf('Adim = %.3f \n', h);
toplam=0;
x=1;
for i=1:n
y=3*(x+(h/2))^2;
fprintf('%d. alan=%.3f\n', i,y);
x=a+i*h;
toplam=toplam+h*y;
end;
fprintf('yaklasik integral = %.3f \n', toplam);
2. Yamuk Yöntemi
İntegrali bulunacak eğri ilgili aralıkta küçük yamuklara ayrılır, bu yamukların alanları
toplanarak yaklaşık sonuç bulunur.
Algoritma;
y
f(x 5)
[a,b] aralığı n eşit parçaya bölünür.
f(x 6)
f(x)
f(x 4)
f(x 1)
f(x 0)
f(x 2)
Yamuklar elde edilir.
f(x 3)
I1 I2
a=x 0
x1
I3
I4
x2
x3
I5
x4
Herbir yamuğun alanı hesaplanır.
I6
x5
b=x 6
x
Alanlar toplaranak yaklaşık integral sonucu bulunur.
b
I
I1 I 2 I 3 I 4 I 5 I 6
f x dx
a
I1
I2
I3
I4
I5
I6
h
2
h
2
h
2
h
2
h
2
h
2
f x 0 f x1
f x1 f x 2
f x2 f x3
f x3 f x4
f x4 f x5
f x5 f x6
b
I
h
2
f x dx
a
f x 0 f x1 f x1 f x 2 f x 2 f x 3 f x 3 f x 4 f x 4 f x 5 f x 5 f x 6
b
Genel hali
I
f x dx
a
h
2
f x0 f xn 2
n
1
i
1
f xi
Örnek :
7
3 x 2 dx integralini yamuk yöntemini kullanarak bulunuz. (n=3,5,10)
1
Örnek :
S
3
sin x dx integralini yamuk yöntemini kullanarak bulunuz. (n=5,10)
0
n=5 için h
b
a
n
S
3
0
5
0.20944 radyan veya 12
o