taşınım olayları - SABİS

TAŞINIM OLAYLARI
(Heterojen Reaksiyonların Kinetiği ilaveli)
Prof.Dr. Kenan YILDIZ
ŞUBAT 2016
METALURJİ VE MALZEME MÜHENDİSLİĞİ
SAKARYA ÜNİVERSİTESİ / MÜHENDİSLİK FAKÜLTESİ
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
BÖLÜM 1
TAŞINIM OLAYLARI - TEMEL KAVRAMLAR
Taşınım Olayları Nelerdir ?
Taşınım olayları üç temel taşınım olayı kapsamaktadır: Akışkanlar dinamiği, Isı transferi ve
Kütle transferi… Akışkanlar dinamiği momentum taşınımını, Isı transferi enerji taşınımını,
kütle transferi ise çeşitli kimyasal parçacıkların taşınımını incelemektedir.
Taşınım
Olayları
Akışkanlar
Dinamiği
Isı
Taşınımı
Kütle
Taşınımı
Bu üç taşınım olayı çoğu proseste birlikte
meydana gelir. Birçok problem ise “denge”
ve “denge dışı” koşullar altındadır. Denge
dışı koşullar altında birçok proses değişkeni
zamanla değişir. Bu değişimlerin hızları da
inceleme alanına girer. Bu hızlar; ısı
transfer hızı, kütle transfer hızı, momentum
transfer hızı ve reaksiyon hızıdır. İlk üçü bu
dersin içeriğinde olup reaksiyon hızı,
kinetiğin içeriğindedir.
Taşınım Olaylarının İncelendiği Üç Mertebe
Aşağıdaki şekilde büyük bir sistemin şematik gösterimi bulunmaktadır. Şekilde, bir akışkan
karışımının içerisinden aktığı bir cihaz bulunmakta olup burada üç farklı mertebede kütle,
momentum, enerji ve açısal momentum taşınımlarını tarif edebiliriz.
Şekil 1.1. (a) N2 ve O2 içeren bir
makroskobik akış sistemi, (b) akma
halindeki N2 ve O2 makroskobik
sistemin içindeki mikroskobik
bölge, (c) N2 ve O2 molekülleri
arasındaki bir çarpışma
Makroskobik mertebede (Şekil 1.1a), sistemdeki kütle, enerji ve momentumun, sisteme
girenler ve sistemden çıkanlar nedeniyle ve çevreden sisteme giren diğer etkenler nedeniyle
nasıl değiştiği incelenir.
1
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Mikroskobik mertebede (Şekil 1.1b), cihazdaki küçük bir bölgede bulunan akışkan karışımına
ne olduğu incelenir. Bu küçük bölgede kütle, enerji ve momentumun nasıl değiştiği tarif
edilirken buradaki amaç, sistem içindeki hız, sıcaklık, basınç ve konsantrasyon profilleri
hakkında bilgi almaktır.
Moleküler mertebede (Şekil 1.1c), moleküler yapı ve moleküller arası kuvvetler temelinde
kütle, enerji ve momentum taşınım mekanizmalarının anlaşılabilmesi için inceleme
yapılmaktadır. Genel olarak bu mertebe teorik fizikçilerin veya fizikokimyacıların ilgi alanına
girmektedir.
BAZI KAVRAMLAR
Denge Prosesleri. Termodinamik genelde dengede bulunan sistemlerle ilgilenir. Örneğin
Şekil 1 de bulunan bir gaz tankını ele alalım. 2 atm ve 300 K de bulunan tankın içinde 50
mol% azot gazı ve 50 mol% oksijen gazı bulunsun. Bu tankın etrafında da aynı sıcaklıkta
ortamdaki havayla çevrili olduğunu kabul edelim.
Şekil 1. Gaz tankı
Belirli bir zaman sonunda, tank içindeki gaz fiziksel dengededir. Sıcaklık, çevrenin sıcaklığı
ile aynıdır. Tank içinde de bir konsantrasyon gradyantı (farklılık) olmayacaktır. Her ne kadar
kimyacılar azot ile oksijen arasında bazı bileşikler olabileceğini söylese de reaksiyon hızı
hemen hemen sıfır olduğundan bu bileşikler oluşmayacaktır. Eğer tankın içinde sadece azot
bulunsaydı bu durumda hem fiziksel hem de kimyasal dengede oluştuğunu söylemek gerekir.
Hız Prosesleri. Denge dışı prosesleri göz önüne alındığı zaman sistem dengeye ulaşmaya
çalışacaktır. Bu tip hız prosesleri bir itici güç ile (driving force) karakterize edilmektedir.
Taşınım hızları bu itici güçlerle orantılı (ilişkili) olup daha ileriki konularda ele alınacaktır.
Sıcaklık. Sıcaklık, bir ampirik (deneysel) ölçü olarak tariflenmektedir. Sıcaklık skalası,
malzemelerin özelliklerinin sıcaklıkla değişimine göre baz alınmıştır. Platin gibi bir katının
özdirencindeki değişim veya cıva gibi bir sıvının hacmindeki değişim, kolaylıkla sıcaklığa
bağlı olarak ölçülebilir ve bu nedenle sıcaklığın ölçülmesinde kullanılabilir. Mevcut
kullanımdaki sıcaklık skalası, suyun tek bir sabit noktasıyla (273.16 K) tariflenmektedir.
Sıcaklık birimleri Kelvin (K), Celcius (oC), Fahrenheit (oF) ve Rankine (oR) dir. Sıcaklık bir
sistemin en önemli özelliklerinden biridir. Moleküllerin hareketine neden olur. Daha yüksek
sıcaklık, daha hızlı moleküller demektir. Hemen hemen bütün özellikler sıcaklığa kuvvetli
şekilde bağlıdır.
2
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Basınç. Şekil 1 de verilen tanktaki basınç, birim alandaki (A) birim kuvvet (F) dir. Kuvvet,
moleküllerin tankın duvarına çarpması sonucu meydana gelir. Basınç bütün yönlerde eşittir.
Denge anında tankın içindeki basınç üniformdur yani aynıdır. Basınç ile kuvveti tartışmak
önemlidir. Kuvvet, basınç çarpı alana eşittir. Şekil 1 deki tank dikdörtgen şekilli olup 4 m
genişliğinde, 2 m yüksekliğinde ve enindedir. Bu nedenle ön yüzdeki toplam kuvvet, yan
uçlardan iki kat daha fazladır, çünkü yüzey alanı iki kat daha fazladır.
Hacim. Anlaşılması en kolay değişken hacimdir. Bir hal denklemi, malzemenin hacmini (V)
sıcaklık (T), basınç (P) ve kompozisyon veya toplam mol (n) sayısıyla ortaya koyar. İdeal gaz
için hal denklemi,
𝑃𝑉 = 𝑛𝑅𝑇
olup burada R gaz sabitidir.
Konsantrasyon. A parçacıklarının konsantrasyonu (CA), birim hacimdeki mol (veya kütle)
sayısıdır. Aşağıdaki örnekte konsantrasyon hesaplaması yapılmıştır.
Örnek. Şekil 1 deki azot gazının konsantrasyonunu hesaplayınız. Gazın ideal davranış
gösterdiğini kabul ediniz.
𝑛=
𝑃𝑉
=
𝑅𝑇
(2 𝑎𝑡𝑚)(16 𝑚3 )
= 1,3 𝑘𝑚𝑜𝑙
𝑎𝑡𝑚. 𝑚3
(0,082
) (300 𝐾)
𝑘𝑚𝑜𝑙. 𝐾
Tank içinde azotun mol fraksiyonu 0.5 olduğu için, tanktaki azot miktarı 0,65 kmol’dür. Bu
durumda azot konsantrasyonu,
𝐶𝐴 =
0,65 𝑘𝑚𝑜𝑙
= 0,0406 𝑘𝑚𝑜𝑙/𝑚3
16 𝑚3
veya
𝐶𝐴 =
650 𝑚𝑜𝑙
= 0,0406 𝑚𝑜𝑙/𝑙𝑡
16000 𝑙𝑡
Kayma Gerilmesi (Shear Stress). Kayma gerilmesi de birim alandaki kuvvettir yani bir
basınçtır. Kayma gerilmesinin bir ya da bütün yönlerde bileşenleri vardır, bunun aksine basınç
bir yüzeye doğru hareket eder.
Şekil 2 de verilen basit bir kayma gerilmesi örneğini göz önüne alalım. 2 m2 lik bir alana
sahip bir blok, beton zemine yerleştirilmiştir. Alttaki bloğa tutkalla tutturulmuş üstteki bloğa 5
N’luk bir kuvvet uygulanmaktadır. Tutkal üzerindeki kayma gerilmesi 2 m2 lik alana 5 N dur,
yani 2.5 N/m2 dir. Tutkal üzerindeki basınç, atmosferik basınca ilaveten üstteki bloğun
ağırlığının (yerçekimi nedeniyle) alana bölümüdür.
3
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Akış (Flux). Akış, birim zamanda birim alandaki miktardır. Isı akışlarındaki kullanılan
terimler genelde Btu, cal ve J olduğu için ısı akışının terimleri J/m2sn gibi terimlerle ifade
edilir. Benzer şekilde kütle akışındaki terim kg/m2sn şeklinde olabilir.
Fazlar. Maddeler katı, sıvı ve gaz halinde bulunurlar. Belirli bir sistemde sadece bir gaz fazı
bulunur, ancak birden fazla katı veya sıvı faz bulunabilir. Örneğin yarısı suyla dolu bir tanka
az miktarda ham petrol ilave edildiği zaman, denge anında altta su ve onun üzerinde yüzen
hidrokarbonlar olmak üzere iki sıvı faz, bunların üzerinde de hava, su molekülleri ve
hidrokarbon moleküllerini içeren bir gaz fazı bulunacaktır. Taşınım olayları genelde birkaç
fazın bulunduğu sistemlerde meydana gelmektedir. Doğal olarak bu tür problemlerin çözümü,
tek fazlı problemlerin çözümünden daha karmaşıktır.
Kuvvet. Kütle ile kuvvet arasındaki ilişki Newton’un 2.hareket kanunuyla verilmektedir.
𝐹 = 𝑚. 𝑎
Burada “a” ivmedir. Bazen bu denkleme dönüşüm faktörü “gc” ilave edilir. Bu terim yer
çekimi sabitidir.
𝐹 = 𝑚. 𝑎/𝑔𝐶
Isı Transferi. Termodinamik ile bir sistemin çevreyle etkileşimi sonucu enerji transferinin
gerçekleşebileceği öğrenilmektedir. Diğer bir ifadeyle, bir sistemin bir halden diğer bir hale
dönüşümü esnasında transfer edilen ısı miktarıyla termodinamik bilimi ilgilenmektedir.
Prosesin ne kadar süreceği ile ilgilenmemektedir. Buna karşılık mühendislikte daha çok ısı
transfer hızıyla ilgilenilmektedir.
Bu durumda birkaç soru ortaya çıkmaktadır. Isı transferi nedir ? Isı nasıl transfer olur ? Niçin
önemlidir? Isı transferi, sıcaklık farklılığı nedeniyle geçiş halindeki termal enerjidir. Bir
ortamda veya ortamlar arasında ne zaman bir sıcaklık farklılığı oluşursa, ısı transferi
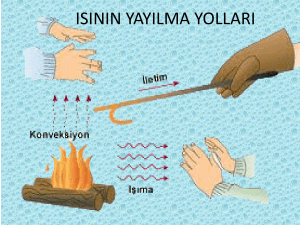
gerçekleşir. Üç temel ısı transferi mekanizması vardır: Konveksiyon, Kondüksiyon ve
Radyasyon.
Şekil 3. Isı transfer türleri ve örnekleri
Kondüksiyon, bir maddedeki daha enerji yüklü parçacıklardan, bitişiğindeki daha az enerji
yüklü parçacıklara enerjinin transferidir.
Konveksiyon, bir katı yüzeyi ile bitişiğinde ve hareket halinde olan sıvı veya gaz arasındaki
ısı transferidir. Kondüksiyon ve akışkan hareketinin birleşik etkilerini içerir.
4
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Radyasyon, atom veya moleküllerin elektronik konfigürasyonundaki (düzenindeki)
değişimlerinin sonucu olarak elektromanyetik dalgalar (veya fotonlar) formunda madde
tarafından dışarıya yayılan enerjidir.
Isı Transferine Pratik Örnek. Pratik uygulamalarda transfer
edilen ısı miktarından daha ziyade ısı transfer hızıyla (birim
zamandaki ısı transferi) ilgilenilir. Örneğin bir termos
içindeki sıcak kahvenin 90oC den 80oC ye soğuması
esnasındaki transfer edilen ısı miktarını termodinamik
analizle tespit edebiliriz. Ancak termos kullanıcısı veya
üreticisi, daha çok termos içindeki sıcak kahvenin ne kadar
sürede 80oC ye düşeceği ile ilgilenmektedir. Bir sisteme ya
da sistemden ısı transfer hızları tespit etme, ısıtma veya
soğutma sürelerini belirleme, ısı transferinin ana konusudur.
Kütle Transferi. Kütle transferi bir akışkanın akmasından farklı bir olaydır. Bu durum, iki
farklı madde temas haline geldiğinde veya iki bileşen içeren bir sistemde, malzeme dağılımı
üniform (benzer, aynı) değilse, bir bünyeden diğer bünyeye moleküllerin taşınması olayıdır.
Metalurji ve Malzeme Mühendisliğinde kütle
transfer olaylarının gerçekleştirildiği birçok
proses vardır. Bunlardan biri, düşük ve orta
karbonlu çelik yüzeylerinin sertleştirilmesi
işlemidir. Karbon içeriği az olduğu için
kırılgan olmayan ve darbe direnci yüksek
olan malzemeye, yüzeydeki aşınma direncini
arttırmak amacıyla, örnek olarak yüzeye
karbon transferi sağlanarak, yüzeyde daha
farklı mekanik özelliklere sahip (örneğin
aşınmaya karşı daha dirençli) bir yapı
oluşturulmasını sağlamaktır.
5
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
BÖLÜM 2
AKIŞKANLAR VE VİSKOZİTE
Akışkanların Akma Tipleri
Akışkanlar bir sistem içinde hareket ettiklerinde, iki farklı akma tipinden biri gerçekleşir. Bu
akma tipleri Laminar (tabakalı) ve Türbülans şeklinde olup şematik olarak Şekil 2.1 de
verilmiştir.
İçerisinden su geçen saydam bir boruyu göz önüne
alalım. İpliksi (ince çizgiler halinde) bir boya
akımını su akışına paralel şekilde suya enjekte
edelim. Çok küçük su hızlarında boya da düz
çizgiler halinde paralel olarak akacaktır. Suyun hızı
arttığı zaman, suyun renkleneceği bir noktaya
ulaşılır. Diğer bir deyişle, sıvının varsayımsal olarak
her bir partikülü, borunun uzunluk eksenine paralel
olarak akma yerine, su ve boyanın tamamen
karışmasına neden olarak şekilde düzensiz olarak
akar. İlk türdeki boya akışı laminar akma (kat kat, Şekil 2.1. Laminar ve Türbülans akma
tabakalı) olarak isimlendirilir. İkinci tür akmaya ise
türbülans akma adı verilmektedir.
Türbülans akmada akışkan partiküllerinin hareketi düzensizdir ve bu olay hızdaki
dalgalanmalarla birlikte gerçekleşir. Bu tip akma Şekil 2.2 de şematik olarak gösterilmiştir ve
(a) kısmında tek bir partikülün bir zaman aralığındaki düzensiz yol almasını göstermekte, (b)
kısmı ise akışkandaki belirli bir noktadaki hızın yaklaşık ortalama bir değerle rasgele
değiştiğini göstermektedir. Bu ortalama değere, 𝑉̅𝑥 sembolüyle verilen anlık ortalama hız
denir.
Şekil 2.2. Türbülans akış. (a) Anlık hız OA, yön ve şiddet olarak sürekli değişir.
/
OB hızı ise x-yönündeki bileşendir ve 𝑣𝑥 ile simgelenmiştir.
/
(b) Zamana bağlı ortalama hızla, 𝑉̅𝑥 , ilgili olarak 𝑣𝑥 ’in O noktasındaki değişimi
6
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Yuvarlak borularda akma türünü belirlemek üzere bir Reynolds Sayısı (Re) vardır. Bu sayı,
𝑅𝑒 =
̅𝐷
𝑉
(2-1)
𝑣
̅ ortalama akışkan hızı, D boru çapı ve v kinematik (hareketle ilgili)
olup denklemdeki 𝑽
viskozitedir ve,
𝜈=
𝜂 (𝑣𝑖𝑠𝑘𝑜𝑧𝑖𝑡𝑒)
(2-2)
𝜌 (𝑦𝑜ğ𝑢𝑛𝑙𝑢𝑘)
denklemiyle bulunur. Bu durumda Reynolds sayısı,
𝑅𝑒 =
̅𝐷
𝜌𝑉
(2-3)
𝜂
denklemiyle bulunabilir. Reynolds sayısı boyutsuzdur yani birimi yoktur. Laminar akıştan
türbülans akmaya geçilen noktada Re sayısı, borulardaki mühendislik akma uygulamalarında
yaklaşık olarak 2300 dür. Boru içerisinde sıkıştırılmayan bir akışta Re sayısı 2300 den büyük
ise türbülanslı akış, küçük ise laminar akış elde edilir. Ancak bu Reynolds sayısı farklı
sistemlerde, hatta belirli bir sistemdeki yüzey pürüzlülüğü gibi dış faktörlere bağlı olarak
değişebilir.
Şekil 2.3’de laminar ve türbülans akış için,
bir boru çapı boyunca hız dağılımını
göstermektedir. Anlık ortalama hız,
türbülans akış için çizilmiştir. Türbülans
akışa ele alındığında, genelde anlık
ortalama değerle ilgileniriz, yani aksi
söylenmedikçe anlık ortalama değer kabul
edilecektir. Her iki akma türünde de
akışkan-duvar arayüzeyinde hız sıfırdır.
Laminar akmada hız profili paraboliktir.
Türbülans akmada eğri ortada bir miktar
düzleşmiştir.
Şekil 2.3. Bir boruda türbülans ve laminar
hızların dağılımı
Örnek 2.1. 40 m uzunluğunda ve 12.7 mm
çapındaki bir borudan 2,81 m/s ortalama hızına
sahip bir akışkan yağ iletilmektedir. Bu
akışkanın yoğunluğu 857 kg/m3, viskozitesi ise
32 cP olduğuna göre gerçekleşecek olan akma
olayının laminar mı yoksa türbülans şeklinde mi
gerçekleşeceğini tespit ediniz.
Yağ
D = 12.7mm
L = 40m
Çözüm. (1 cP = 10-3 kg/m.s)
7
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑘𝑔
𝑚
−3
𝜌 𝑉̅ 𝐷 (857 𝑚3 ) (2,81 𝑠 ) (12,7. 10 𝑚)
𝑅𝑒 =
=
= 955,7
𝑘𝑔
𝜂
32. 10−3 𝑚. 𝑠
Değer 2300 sayısından düşük olduğuna göre laminar akış gerçekleşecektir.
Örnek 2.2. 0,24 m çapındaki ve 20 m uzunluğundaki bir borudan 1,17 kg/m3 yoğunluğunda
ve 1,92.10-5 kg/m.s viskozitesine sahip bir akışkan madde iletilmektedir. Akışkan maddenin
ortalama akma hızı 8,33 m/s olduğuna göre akma türünü tespit ediniz.
Çözüm.
𝑘𝑔
𝑚
𝜌 𝑉̅ 𝐷 (1,17 𝑚3 ) (8,33 𝑠 ) (0,24 𝑚)
𝑅𝑒 =
=
= 121826,25
𝑘𝑔
𝜂
−5
1,92. 10
𝑚. 𝑠
Bu değer 2300 sayısından büyük olduğu için türbülans akış gerçekleşecektir.
Problem (2014 Vize-A Grubu): Yoğunluğu 1 g/cm3, viskozitesi ise 0,001545 kg/m.s olan 4°C
deki suyun 91,4 cm/s hızda 10 m uzunluğundaki yatay bir borudan laminar türde akması için
kullanmanız gereken borunun maksimum çapı kaç mm olmalıdır?
Çözüm.
𝐷=
𝑅𝑒 𝑥 𝜂
̅
𝜌𝑥𝑉
=
𝑘𝑔
𝑚.𝑠
𝑘𝑔
𝑚
1000 3 𝑥 0,914
𝑠
𝑚
2300 𝑥 0,001545
= 3,88. 10−3 𝑚 = 3,88 𝑚𝑚
Problem (2014 Vize-B Grubu): Yoğunluğu 1 g/cm3, viskozitesi ise 0,001545 kg/m.s olan 4°C
deki suyun 75,4 cm/s hızda 15 m uzunluğundaki yatay bir borudan laminar türde akması için
kullanmanız gereken borunun maksimum çapı kaç mm olmalıdır?
Çözüm.
𝐷=
𝑅𝑒 𝑥 𝜂
̅
𝜌𝑥𝑉
=
𝑘𝑔
𝑚.𝑠
𝑘𝑔
𝑚
1000 3 𝑥 0,754
𝑠
𝑚
2300 𝑥 0,001545
= 4,71. 10−3 𝑚 = 4,71 𝑚𝑚
Newton Akışkanları
Şekil 2.4’de verilen, iki levha arasındaki bir akışkanı ele alalım. Üstteki levha sabit, alttaki
levha ise sıfır zamanında (başlangıçta) V hızıyla hareket halinde düzenlenmiş olsun.
Levhaların bitişiğindeki akışkan, levhalarınki ile aynı hıza sahip olacaktır. Böylece alt levhaya
bitişik olan akışkan V hızında hareket ederken, üst levhaya bitişik olan önemsiz (sıfır) bir hıza
sahip olacaktır. Zaman ilerledikçe akışkan bir momentuma (momentum: hareket eden bir
kütledeki hareket miktarı) sahip olacak, belirli bir zaman geçildikten sonra sabit hale ulaşılır.
Burada alttaki levhayı V hızında hareket halinde tutmak için bir F kuvveti uygulanmalıdır,
eşit ancak zıt bir kuvvette bir kuvvet sabit levhada uygulanmaktadır (oluşmaktadır).
8
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Şekil 2.4. Paralel levhalar arasındaki akışkanın laminar akması
Sabit halde ve laminar akmada, A alanına sahip levhalar için kuvvet,
𝐹
𝐴
𝑉
= 𝜂𝑌
(2-4)
Olup burada Y levhalar arasındaki mesafe ve 𝜼 orantılılık sabitidir. Tarif edilen şekliyle
kuvvet kesmedir ve birim alandaki kuvvet (F/A) ise kayma gerilmesidir. Sabit halde hız
profili lineer olduğu zaman V/Y ifadesi yerine sabit hız gradyantı, 𝑑𝑣𝑥 /𝑑𝑦 , yazılabilir.
Herhangi iki ince akışkan tabaka arasındaki kayma gerilmesi, 𝜏𝑦𝑥 , aşağıdaki denklemle ifade
edilebilir.
𝜏𝑦𝑥 = −𝜂
𝑑𝑣𝑥
𝑑𝑦
(2-5)
Denklem (2-5) alternatif olarak momentum taşınımı terimiyle de ifade edilmektedir.
Levhalara paralel olarak bir seri ince akışkan tabakaları göz önüne alın. Her bir tabaka
kendiyle birlikte oluşan bir momentuma sahiptir ve tabaların birbiri üzerinde hareket
etmelerine neden olur. Böylece momentum y-yönünde taşınır. Denklem (2-5) deki eksi (-)
işareti, momentumun alttaki akışkan tabakasından üstteki tabakaya (pozitif y yönünde)
taşındığı gerçeğini ifade eder. Bu durumda 𝑑𝑣𝑥 /𝑑𝑦 negatif olup 𝜏𝑦𝑥 değeri pozitif olacaktır.
Alttaki levhanın harekete başladığı t = 0 anı ile sabit hale ulaşılan büyük t zamanı arasındaki
periyod, kısa süreli periyod olarak adlandırılır. Kısa süreli periyod esnasında vx hem zamanın
hem de pozisyonun fonksiyonudur, bu durumda
𝜏𝑦𝑥 için daha genel bir ifade
kullanılmaktadır.
𝜏𝑦𝑥 = −𝜂
𝜕𝑣𝑥
𝜕𝑦
(2-6)
Bu denklem, Newton’un Viskozite Kanunu olarak bilinmektedir ve orantılılık sabitini 𝜼
viskozite olarak tariflendirmektedir. Viskozitenin birimi İngiliz sistemine göre kg/saat.cm
olup CGS sisteminde poise (P) kullanılır. 1 poise = 1 dyn.sn/cm2 değerine eşittir. Sentipoise
(cP) birimi de viskozite için en çok kullanılan birimdir ve 0.01 poise değerine eşittir. Bu
değer, yaklaşık 20oC deki suyun viskozitesidir.
Kinematik viskozite, termal ve kütle difüzyonundakine benzer şekilde momentum
difüzitesinin ölçümünde temel bir miktardır. CGS sisteminde birimi cm2/saniye olup stoke
olarak isimlendirilir. Sentistoke (0.01 stoke) terimi de çok kullanılmaktadır.
9
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
1 cP = 1.10-3 kg/m.sn = 1.10-5 kg/cm.sn = 0,01 g/cm.sn
Örnek 2.3. İki paralel levha arasında 0,3175 cm mesafe bulunmaktadır. Alttaki levha sabit,
üstteki levha ise 152,4 cm/sn hızla hareket etmektedir. Üst levhadaki kayma gerilmesi 0,024
kg/cm.sn2 olduğuna göre levhalar arasındaki akışkanın vizkozitesini bulunuz.
Çözüm:
𝜂=
𝐹
𝐴
𝑘𝑔
𝐹/𝐴
𝑉/𝑌
𝑉
(𝐾𝑎𝑦𝑚𝑎 𝐺𝑒𝑟𝑖𝑙𝑚𝑒𝑠𝑖) = 0,024 𝑐𝑚.𝑠𝑛2
𝜂=
𝑌
=
152,4 𝑐𝑚/𝑠𝑛
0,3175 𝑐𝑚
= 480 𝑠𝑛−1
0,024 𝑘𝑔. 𝑐𝑚−1 . 𝑠𝑛−2
= 5. 10−5 𝑘𝑔. 𝑐𝑚−1 . 𝑠𝑛−1 = 5 𝑐𝑃
480 𝑠𝑛−1
Örnek 2.4. Altta sabit bir levha ile üst kısımda 60 cm/sn
hızda hareket eden bir levha arasında 0,16 cm mesafe
bulunmaktadır. Bu iki levha arasından geçen akışkanın
viskozitesi 2 cP olduğuna göre kesme gerilmesini
bulunuz.
Çözüm:
𝑔
𝑐𝑚
0,01 𝑐𝑚. 𝑠𝑛 60 𝑠𝑛
𝐹
𝑉
𝑔
𝐾𝑎𝑦𝑚𝑎 𝐺𝑒𝑟𝑖𝑙𝑚𝑒𝑠𝑖 ( ) = 𝜂 . = 2 𝑐𝑃 .
𝑥
= 7,5
𝐴
𝑌
1 𝑐𝑃
0,16 𝑐𝑚
𝑐𝑚. 𝑠𝑛2
Örnek 2.5. Birbirine paralel iki levhadan alttaki sabit üstteki ise 0,8 m/sn hızında hareketlidir.
Kayma gerilmesi 4000 g/cm.sn2 olup 100 poise gibi yüksek viskoziteli bir akışkan yağın
bulunduğu iki levha arasındaki mesafeyi bulunuz.
Çözüm:
100 poise = 10000 cP
𝐹/𝐴
𝜂 = 𝑉/𝑌 denkleminden,
𝑔
𝑔
0,01 𝑐𝑚. 𝑠𝑛 4000 𝑐𝑚. 𝑠𝑛2
10000 𝑐𝑃 .
=
𝑐𝑚
1 𝑐𝑃
80 𝑠𝑛
𝑌
𝑔
𝑔
100
= 50
𝑥𝑌
𝑐𝑚. 𝑠𝑛
𝑐𝑚2 . 𝑠𝑛
𝑌 = 2 𝑐𝑚
Problem (Ödev 1, 2014): İki paralel levha arasındaki bir akışkanın viskozitesi 10 cP olup alt
levha 0,5 m/s hızla hareket etmektedir. Kayma gerilmesi 0,05 kg/cm.s2 olduğuna göre
levhalar arası mesafeyi bulunuz. 1 cP = 10-3 kg/m.s
Çözüm.
𝐹
𝑉
=𝜂
𝐴
𝑌
10
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑚 100 𝑐𝑚
𝑘𝑔
𝑘𝑔
1 𝑚 0,5 𝑠 . 1 𝑚
−3
0,05
= 10. 10
.
.
𝑐𝑚. 𝑠 2
𝑚. 𝑠 100 𝑐𝑚
𝑌
𝑌 = 0,1 𝑐𝑚
Gazların Viskozitesi
Gazlardaki momentum (hareket eden bir kütledeki hareket miktarı) taşınımını izah etmek için,
gazların kinetik teorisine başvururuz. Molekülleri bilardo topları gibi idealize ederek,
ortalama serbest yol kavramını kullanırız ve aşağıdaki özellikleri gösteren hipotetik
(varsayımsal, farazi) bir gazı varsayarız.
a) Moleküller “m” kütlesine ve “d” çapına sahip bilardo topları gibi sert kürelerdir.
b) Çarpıştıkları zaman hariç, moleküller birbiri üzerinde kuvvet uygulamazlar.
c) Çarpışmalar mükemmel şekilde elastiktir, klasik kütle ve enerji korunumu
kanununa uyarlar.
d) Moleküller gaz içerisinde birim hacimde bir “n” konsantrasyonunda üniform olarak
dağılırlar. Sürekli hareket halindedirler ve çaplarına nazaran geniş aralıklarla ayrılırlar.
e) Bütün yönlerdeki moleküler hızlar eşittir. Bir molekülün hızı sıfırla sonsuz arasında
herhangi bir değere sahip olabilir.
Moleküllerin bir Maxwellian hız dağılımına (örneğin gazların termal enerjisi, hareket eden
bütün moleküllerin toplam kinetik enerjisiyle verilir) sahip olduğunu kabul edersek, bu
durumda ortalama hız, 𝑉̅ ;
8𝜅𝐵 𝑇
𝑉̅ = √ 𝜋𝑚
(2-7)
olup burada 𝜅𝐵 Boltzman sabiti, T ise mutlak sıcaklıktır.
İlave olarak bu tür moleküller için gazlarda momentum transfer mekanizmasını belirleyen
önemli bir parametre (değişken), iki başarılı çarpışma arasında bir molekül tarafından
katedilen mesafe olarak tanımlanan serbest yol’dur. Çarpışma anında iki molekülün
merkezleri arasında mesafe “d” dir. Ortalama serbest yol “λ”, πd2 ile ters orantılı, ayrıca
moleküllerin “n” konsantrasyonuyla da ters orantılı olmalıdır. Sonuç olarak gaz molekülleri
için ortalama serbest yol,
1
1
𝜆 = ( ) (𝜋𝑑2 𝑛)
√2
(2-8)
şeklinde ifade edilebilir.
11
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Şekil 2.5. Hız profili ile y1 düzlemi arasındaki ilişki
Moleküllerin hareket ettiği ve y = y1 olan bir hayali düzlem göz önüne alalım (Şekil 2.5).
Gazda y – yönünde makroskobik akmanın olmadığı koşulları incelersek, y1 düzlemi boyunca
bulunan moleküller eşit frekansa sahiptirler. y1 düzlemi boyunca bir taraftan geçen
moleküllerin birim alandaki frekansı,
1
𝑍 = 4 𝑛𝑉̅
(2-9)
denklemiyle verilmektedir.
Çarpışma sonrasında y1 düzleminin aşağısına veya yukarısına 𝑦̅ mesafesi kadar momentum
taşınımı olduğunu düşünelim. Sayısal olarak 𝑦̅ mesafesi λ değerine tam olarak eşit değildir ve
genelde aşağıdaki denklemle hesaplanmaktadır.
2
𝑦̅ = 3 𝜆
(2-10)
Bu noktaya kadar gazın makroskobik akışının olmadığını göz önüne almıştık, çünkü yukarıda
ifade edildiği gibi y1 ‘in aşağısı ve yukarısına giden molekül sayısı eşittir ve y düzlemi
boyunca ortalamada net bir momentum transfer olmamaktadır.
Gazın viskozitesini tespit etmek için, Şekil 2.5 de şematize edildiği gibi, x – yönünde dvx/dy
hız gradyantına sahip makroskobik akma etkisi altındaki gazı göz önüne alacağız.
y1 üzerindeki x – momentumu,
2
{𝑚𝑣𝑥 }𝑦1+𝑦̅ = {𝑚𝑣𝑥 }𝑦1 + 𝜆𝑚
3
𝑑𝑣𝑥
𝑑𝑦
(2-11)
Benzer şekilde y1 altında,
2
{𝑚𝑣𝑥 }𝑦1−𝑦̅ = {𝑚𝑣𝑥 }𝑦1 − 𝜆𝑚
3
𝑑𝑣𝑥
𝑑𝑦
(2-12)
İkisi arasındaki fark, bize net x – momentum hızını vermektedir.
12
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝜏𝑥𝑦 = 𝑍𝑚[{𝑣𝑥 }𝑦1 −𝑦̅ − {𝑣𝑥 }𝑦1+𝑦̅ ]
(2-13)
Denklem (2-9), (2-11) ve (2-12) kombine edildiğinde,
1
𝑑𝑣
𝜏𝑥𝑦 = − 3 𝑛𝑚𝑉̅ 𝜆 𝑑𝑦𝑥
(2-14)
elde edilir. İlave olarak 𝑉̅ ve λ yerine uygun ifadeleri yazdığımızda,
2
𝜏𝑥𝑦 = − 3𝜋3/2
(𝑚𝜅𝐵 𝑇)1/2 𝑑𝑣𝑥
𝑑2
(2-15)
𝑑𝑦
Bu sonuç, Denklem (2-6) da verilen Newton’un viskozite kanunu ile ilişkilidir.
2
𝜂 = 3𝜋3/2
(𝑚𝜅𝐵 𝑇)1/2
(2-16)
𝑑2
Bu denklemden çıkarılacak önemli sonuç, gazın viskozitesinin basınçtan bağımsız ve sadece
sıcaklığa bağımlı olduğudur. Gazlarda sıcaklık arttıkça viskozite artmaktadır. Buna karşılık bu
artış, miktarsal olarak çok önemli değildir.
Bilardo topları modelinin yerini alan ve
daha güncel olan kinetik teoriler,
moleküller arasında itme ve çekme
kuvvetlerini göz önüne alarak daha
gerçekçi bir moleküler kuvvet alanını
içermektedir. Bu teoriler, gazdaki bir
çift molekül arasındaki potansiyel
etkileşim enerjisini kullanmaktadır.
Lennard–Jones Potansiyeli olarak da
bilinen bu potansiyel, uzak mesafelerde
zayıf etkileşimleri (çekme) ve yakın
mesafelerde kuvvetli etkileşimleri
(itme) içermektedir. Şekil 2.6 da iki
polar olmayan (kutupsuz) molekülün Şekil 2.6. İki kutupsuz (nonpolar) molekülün
etkileşimini tarifleyen Lennard-Jones etkileşimini tarifleyen Lennard-Jones potansiyel
fonksiyonu
potensiyel fonksiyonu gösterilmiştir.
Moleküllerin denge pozisyonu δ noktasında olup burada potansiyel enerji, minimum – ε
noktasındadır. Buradaki ε terimi, karakteristik enerji parametresidir. Chapman & Enskog
isimli bilim insanları, Lennard-Jones potansiyelini kullanarak, düşük sıcaklıklarda kutupsuz
gazların viskozitesi için aşağıdaki denklemi geliştirmişlerdir.
√𝑀.𝑇
𝜂 = 2,67. 10−5 𝜎2 Ω
𝜂
(2-17)
Burada M moleküler ağırlık, T mutlak sıcaklık (K), σ ise moleküllerin karakteristik çapıdır
(A). Ωη terimi, Chapman-Enskog teorisinin çarpışma integrali (unsuru) olup boyutsuz sıcaklık
parametresi olan 𝜅𝐵 𝑇/𝜀 teriminin bir fonksiyonudur. Denklem (2-17) yi kullanmak için σ ve
13
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝜀/𝜅𝐵 değerlerine ihtiyacımız vardır. Bu parametreler birçok madde için bilinmektedir ve
bazılarının ki Tablo 2.2 de verilmiştir. Tablo 2.3 kullanılarak çarpışma integrali de tespit
edilebilir.
Tablo 2.2. Moleküllerarası kuvvet parametreleri ve kritik özellikler
Madde
Moleküler
Ağırlık (M)
Lennard-Jones parametreleri
σ (oA)
𝜀/𝜅𝐵 (oK)
Kritik sabitler
Tc (oK)
𝑉̅𝑐 (cm3/g.mol)
Hafif elementler
H2
He
2,016
4,003
2,915
2,576
38
10,2
33,3
5,26
65
57,8
Asal gazlar
Ne
Ar
Kr
Xe
20,183
39,944
83,8
131,3
2,789
3,418
3,498
4,055
35,7
124
225
229
44,5
151
209,4
289,8
41,7
75,2
92,2
118,8
Basit poliatomik maddeler
Hava
28,97
N2
28,02
O2
32
CO
28,01
CO2
44,01
SO2
64,07
F2
38
Cl2
70,91
Br2
159,83
CH4
16,04
3,617
3,681
3,433
3,590
3,996
4,290
3,653
4,115
4,268
3,822
97
91,5
113
110
190
252
112
357
520
137
132
126,2
154,4
133
304,2
430,7
417
584
190,7
86,6
90,1
74,4
93,1
94
122
124
144
99,3
Tablo 2.3. Lennard-Jones potansiyeli için Ωη ve 𝜅𝐵 𝑇/𝜀 değerleri
𝜅𝐵 𝑇/𝜀
Ωη
f(𝜅𝐵 𝑇/𝜀)
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
2,0
4,0
6,0
8,0
10
20
40
60
80
100
200
400
2,785
2,492
2,257
2,065
1,908
1,780
1,675
1,587
1,175
0,9700
0,8963
0,8538
0,8242
0,7432
0,6718
0,6335
0,6076
0,5882
0,5320
0,4811
0,1969
0,2540
0,3134
0,3751
0,4384
0,5025
0,5666
0,6302
1,2048
2,0719
2,751
3,337
3,866
6,063
9,488
12,324
14,839
17,137
26,8
41,9
14
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Şekil 2.7 de sıcaklığın fonksiyonu olarak bazı gazların viskozite değişimleri verilmiştir.
Şekilden gözlenen en belirgin nokta, bütün gazların viskozitesinin, sıcaklığın artması ile
artmasıdır.
Örnek 2.6. 1364 K ve 1 atm’deki hidrojenin viskozitesini hesaplayınız.
Çözüm:
𝜀
Tablo 2.2’den 𝜅 = 38 ve σ = 2,915 oA, Tablo 2.3 den Ωη değeri yaklaşık 0,69 alınabilir.
𝐵
𝜂 = 2,67. 10−5
√(2)(1364)
√𝑀. 𝑇
= 2,67. 10−5
= 2,39. 10−4 𝑝𝑜𝑖𝑠𝑒
2
(2,915)2 (0,69)
𝑑 Ω𝜂
Şekil 2.7. 1 atm’de bazı gazların viskozitesi
Sıvıların Viskozitesi
Sıvılardaki taşınım prosesleriyle ilgili olarak, katıların ve gazların yapılarına nazaran sıvıların
yapıları hakkında daha az bilgi olduğu sorunuyla yüzleşiriz. Bununla birlikte sıvılarla katılar
arasında çok benzerlik vardır. Bu benzerlik, ergimede küçük bir hacim artışı (metallerde %35) temeline ve ergime ısısının, buharlaşma ısısından çok daha az olmasına gerçeğine
dayanmaktadır. X-ışını analizleri, sıvılarda en azından kısa-aralıklı bir düzene sahip olduğunu
bize göstermiştir. Yani bir merkez atomdan kısa bir mesafede, en yakın komşu atomların
düzeni tahmin edilmektedir. Ancak mesafe arttıkça atom pozisyonlarının tahmin edilebilirliği,
katılardaki gibi azalmaktadır.
Sıvıların özellikleri için birkaç teori ortaya konmuştur. En eskisi ise Hole (boşluk) Teorisi’dir.
Bu teoride bir sıvının, sıvı içerisinde dağılmış birçok boşluklara sahip olduğu ifade edilmiştir.
15
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Her ne kadar bu teori ergimede malzemenin özelliklerindeki değişimleri tam olarak
açıklamasa da, sıvıların viskozitesinin sıcaklığa bağımlılığının tespit etmede nispeten basit bir
uygulama çıkarmada faydalı olmaktadır.
Ergime noktalarına yakın sıvılar hala yoğun bir faz gibi bulundukları için, atomdan atoma
momentum transferi kavramı geçersizdir, zira sıvıların sahte latisleri (pseudo lattice) içinde
atomların titreşimi (vibrasyonu) ile her bir atomun momentumu hızla değişmektedir.
Einstein, bir dış kuvvet etkisi altındaki bir partikülün mobilitesi (B), difüzyon katsayısı D ile
ilişkilidir,
𝐷 = 𝐵 𝜅𝐵 𝑇
(2-18)
B, ortalama hızdır. Difüzyon olayı aktive olmuş bir proses olduğu için, minimum aktivasyon
enerjisi Δ𝐺 ⋕ , bir partikülün stabil (kararlı) bir pozisyondan diğerine hareket etmesi için
uygulanması gereken enerjidir. Atomların hareket etme kabiliyetleriyle orantılı olan
akışkanlık, difüzyon gibi termal olarak aktive edilmelidir.
Viskozitenin tersi akışkanlıktır. Her ne kadar D değeri 𝑒𝑥𝑝[−∆𝐺 # /𝑅𝑇] ile orantılı olsa da, bu
durumda viskozite de (η), 𝑒𝑥𝑝[+∆𝐺 # /𝑅𝑇] ile orantılı olmalıdır. Yani sıvıların viskozitesi
sıcaklığın artması ile azalır. Bu durumda sıvılardaki viskozitenin sıcaklıkla ilişkisi,
𝜂 = 𝐴 𝑒𝑥𝑝 [
#
Δ𝐺𝑣𝑖𝑠
𝑅𝑇
]
(2-19)
olup burada η viskozite (poise), A bir sabit (poise), T mutlak sıcaklık (K), R gaz sabiti
(cal/K.mol) ve 𝚫𝑮#𝒗𝒊𝒔 viskozitenin aktivasyon enerjisidir (cal/mol). A sabitini tespit etmede
kullanılan denklem Eyring Teorisi denklemi olup aşağıda verilmiştir
𝐴≅
𝑁0 ℎ
(2-20)
𝑉
Burada N0 Avogadro sayısı, V molar hacim ve h Planck sabitidir. Van der Waals tipi bağ
kuvvetlerinin olduğu moleküler sıvılarda, buharlaşma enerjisinden viskozite aktivasyon
enerjisi yaklaşık olarak tespit edilebilir.
#
∆𝐺𝑣𝑖𝑠
≅ 0.41 ∆𝐻𝐵𝑢ℎ
(2-21)
Tablo 2.4. Çeşitli sıvılar için viskozite aralıkları
Viskozite aralığı (poise)
1 – 100
0.1 – 1
0.01 – 1
0.001 – 0.01
Malzemeler
CaO – Al2O3 – SiO2 curufları
%50 NaOH + %50 H2O
H2SO4
Ergimiş tuzlar
Ağır metaller (Pb, Au, Zn vb.)
Alkali toprak metaller (Ca, Mg)
Geçiş metalleri (Fe, Ni, Co vb.)
Su (70 F)
Kerosen (70 F)
Aseton
Alkali metaller
16
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Maalesef Denklem (2-20) ve (2-21) sıvı metaller için geçerli değildir, ayrıca polimerler ve
başka zinciryapılı moleküllere sahip maddeler için de geçerli değildir. Bu durumu göstermek
için Tablo 2.4 de genel viskozite aralıklarına göre çeşitli malzeme grupları verilmiştir.
Kullanılan viskozite değerleri, normal sıcaklık aralıklarındaki değerlerdir.
Sıvı Metal ve Alaşımların Viskozitesi
Metaller tabiatı gereği moleküler yapıda değildir, bu nedenle ne A sabiti ne de 𝚫𝑮#𝒗𝒊𝒔 değeri
mevcut denklemlerle tespit edilemezler. Şekil 2.8 de bazı metallerin sıcaklığa bağlı viskozite
değişimleri (1/T değerine karşılık log η) verilmiştir. Şekilden görüldüğü gibi sıcaklık arttıkça
(x ekseninde 1/T nedeniyle sola doğru gidildikçe) viskozite değerleri düşmekte, yani sıvı
metallerin akışkanlıkları artmaktadır.
Şekil 2.8. Sıvı metallerin viskozitelerinin sıcaklığa bağımlılıkları
Chapman isimli bilim insanı, viskozite – enerji parametresi (ε) – ayrılma mesafesi (δ) arasında
bir ilişki ortaya koymuştur. Enerji parametresi atomlar arasındaki potansiyel enerjidir.
Ayrılma mesafesi ise atomlararası mesafedir. Sıvı metaller için η* (azalan viskozite), T*
(azalan sıcaklık) ve V* (azalan hacim) arasındaki fonksiyonel ilişki;
𝜂 ∗ ( 𝑉 ∗ )2 = 𝑓 (𝑇 ∗ )
ve
𝜂∗ =
𝑇∗ =
𝜂.𝛿 2 𝑁0
√𝑀𝑅𝑇
𝜅𝐵 .𝑇
𝜀
1
𝑉 ∗ = 𝑛.𝛿3
(2-22)
(2-23)
(2-24)
(2-25)
17
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Buradaki terimler, δ = sıkı paket bir kristalde 0oK de atomlararası mesafe (angstrom), ε =
belirli metalin enerji parametresi, N0 = Avogadro sayısı, M = molekül ağırlık, R = gaz sabiti,
T = mutlak sıcaklık (K), κB = Boltzman sabiti, n = birim hacimdeki atom sayısı.
Saf metallerin viskozite – sıcaklık ilişkisi, bir deneysel parametre (ε/κB) ile düzeltilir. Tablo
2.5 ve Şekil 2.9 kullanılarak bu işlemler gerçekleştirilir. Örnek olması açısından sıvı titanyum
ile ilgili viskozite hesaplaması aşağıdaki örnekte verilmiştir.
Tablo 2.5. Sıvı metaller için deneysel tespit edilmiş (ε/κB) değerleri
Metal
Na
K
Li
Mg
Al
Ca
Fe
Co
Ni
Cu
Zn
Rb
Ag
Cd
In
Sn
Cs
Au
Hg
Pb
Pu
δ (angstrom)
3.84
4.76
3.14
3.20
2.86
4.02
2.52
2.32
2.50
2.56
2.74
5.04
2.88
3.04
3.14
3.16
5.40
2.88
3.10
3.50
3.10
(ε/κB) (K)
1970
1760
2350
4300
4250
5250
10900
9550
9750
6600
4700
1600
6400
3300
2500
2650
1550
6750
1250
2800
5550
Metallerde ergime sıcaklığı ile (ε/κB) arasındaki ilişki ise,
𝜀
𝜅𝐵
= 5.2 𝑇𝐸𝑟𝑔𝑖𝑚𝑒
(2-26)
şeklinde verilmiştir.
Şekil 2.9. Sıvı metallerin viskoziteleri için düzeltme eğrisi
18
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Örnek 2.7. 1850oC de sıvı titanyumun viskozitesini tahmin ediniz. Titanyum için ergime
sıcaklığı 1800oC, molekül ağırlığı 47.9 g/mol, yoğunluğu 4.50 g/cm3 ve δ=2.89 Ao
Çözüm:
𝜀
= 5,2𝑥𝑇𝑒𝑟𝑔 = 5,2𝑥2073 = 10780 𝐾
𝜅𝐵
𝜅
2123
1
𝑇 ∗ = 𝜀𝐵 𝑇 = 10780 = 0.197 (𝑇 ∗ = 5,076)
Yandaki şekilden 𝜂∗ (𝑉 ∗ )2 = 3,6
değeri tespit edilmiştir.
𝑉∗ =
1
= 0.733
6.02𝑥1023 𝑎𝑡𝑜𝑚 4.5 𝑔
−8 𝑐𝑚)3
(2.89𝑥10
(
)
(
)
47.9 𝑔
𝑐𝑚3
Bu durumda,
𝜂∗ =
3.6
3.6
=
= 6.63
(𝑉 ∗ )2 0.7332
𝜂∗ (𝑀𝑅𝑇)1/2 6.63 [(47.9)(8.314𝑥107 )(2123)]1/2
𝜂=
=
= 3.83𝑥10−2 𝑝𝑜𝑖𝑠𝑒 = 3.83 𝑐𝑃
(2.89𝑥10−8 )2 (6.02𝑥1023 )
𝛿 2 𝑁0
Problem (Ödev 2, 2014): (1.ÖĞRETİM) Sıvı kromun 2200°C deki (2473 K) viskozitesini
bulunuz. Kromun mol ağırlığı 52 g/mol, ergime sıcaklığı 1907°C (2180 K), atomik çapı 2,56
A (2,56.10-8 cm) ve yoğunluğu 6,3 g/cm3 alınacaktır.
Çözüm.
𝜀
= 5,2 𝑇𝐸𝑟𝑔 = 5,2𝑥2180 = 11336
𝜅𝐵
𝑇∗ =
𝜅𝐵
2473
.𝑇 =
= 0,218
𝜀
11336
1
1
=
= 4,59
∗
𝑇
0,218
19
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝜂∗ (𝑉 ∗ )2 = 2,9
𝑉∗ =
1
6,02. 1023
52
𝜂∗ =
𝑥6,3𝑥(2,56. 10−8 )3
=
1
= 0,817
1,2236
2,9
2,9
=
= 4,345
(𝑉 ∗ )2 (0,817)2
4,345 √(52)(8,314. 107 )(2473)
𝜂=
= 0,036 𝑝𝑜𝑖𝑠𝑒 (3,6 𝑐𝑃)
(2,56. 10−8 )2 6,02. 1023
(2.ÖĞRETİM) Sıvı bizmutun 500°C deki (773 K) viskozitesini bulunuz. Bizmutun mol
ağırlığı 209 g/mol, ergime sıcaklığı 272°C (545 K), atomik çapı 3,12 A (3,12.10-8 cm) ve
yoğunluğu 10,05 g/cm3 alınacaktır.
Çözüm.
𝜀
= 5,2 𝑇𝐸𝑟𝑔 = 5,2𝑥545 = 2834
𝜅𝐵
𝑇∗ =
𝜅𝐵
773
.𝑇 =
= 0,2727
𝜀
2834
1
1
=
= 3,67
∗
𝑇
0,2727
20
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝜂∗ (𝑉 ∗ )2 = 2
𝑉∗ =
1
6,02. 1023
−8 )3
209 𝑥10,05𝑥(3,12. 10
𝜂∗ =
𝜂=
=
1
= 1,137
0,879
2
2
=
= 1,547
∗
2
(𝑉 )
(1,137)2
1,547 √(209)(8,314. 107 )(773)
= 0,0096 𝑝𝑜𝑖𝑠𝑒 (0,96 𝑐𝑃)
(3,12. 10−8 )2 6,02. 1023
21
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
BÖLÜM 3
ISI TRANSFERİ
Enerji Transferi
Enerji, belirli bir kütleye ya da kütleden iki mekanizma ile transfer edilir: Isı transferi ve İş…
İtici güç sıcaklık farkı olursa enerji transferi ısı transferiyle, aksi takdirde iş yoluyla
gerçekleşir. Birim zamanda yapılan işe (W) güç (power) denir ve birimi W veya hp (horse
power) dir (1 hp = 746 W).
Günlük yaşamımızda iç enerji ifadesi yerine ısı kavramını kullanırız ve bir kütlenin ısı içeriği
hakkında konuşuruz. Örneğin vücut ısısı, bir vücudun termal (ısıl) enerji içeriği anlamına
gelmektedir. Termal enerjiyi “ısı”, termal enerji transferini de “ısı transferi” olarak kabul
edersek, bir proses esnasında transfer edilen ısıyı Q ile, birim zamanda transfer edilen ısı
miktarını (ki buna ısı transfer hızı denir) q* ile simgeleyebiliriz.
𝑄 = 𝑞. ∆𝑡 [J = (J/sn)x(sn)]
Transfer edilen ısı miktarı = Q (J)
Isı transfer hızı (belirli zaman aralığında transfer edilen ısı miktarı) = q (J/sn = W)
Isı akışı (birim alanda bir yönde birim zamandaki ısı transferi) = q* (q*=q/alan) (W/m2)
Isı kaybı (belirli bir alandaki ısı transfer hızı) = q [q=(q*)x(alan)] (W)
Örnek 3.1. 10 cm çapındaki bir bakır bilya 30 dakika içinde
100°C den 150°C ye ısıtılmaktadır. Bilyanın yoğunluğu (d)
8950 kg/m3 ve ısı kapasitesi (Cp) 0.395 kJ/kg.°C olduğuna
göre,
a) bakır bilyaya transfer edilen ısı miktarını bulunuz
b) bilyaya olan ısı transfer hızını bulunuz
c) ısı akışını bulunuz.
Çözüm.
(a)
Sisteme yapılan enerji transferi = Sistemdeki enerji artışı
𝑄 = ∆𝐸 = 𝑚. 𝑐. ∆𝑇
𝜋𝐷
𝜋
𝑘𝑔
𝑚 = 𝑑. 𝑉 = 𝑑. (
) = . (8950 3 ) . (0,1 𝑚)3 = 4,684 𝑘𝑔
6
6
𝑚
𝑘𝐽
𝑄 = (4,684 𝑘𝑔) (0,395
) (150 − 100)°𝐶 = 92,51 𝑘𝐽
𝑘𝑔. °𝐶
Bakır bilyanın sıcaklığını 100°C den 150°C ye çıkarmak için bilyaya 92,51 kJ ısı verilmesi
gerekmektedir.
3
22
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
(b)
𝑞=
𝑄
92510 𝐽
=
= 51,39 𝑊 (𝐽/𝑠𝑛)
∆𝑡 1800 𝑠𝑛
(c)
𝑞∗ =
𝑞
𝑞
51,39 𝑊
𝑊
=
=
= 1636,6 2
2
2
𝐴𝑙𝑎𝑛 𝜋𝐷
𝜋 (0,1 𝑚)
𝑚
Isı Transfer Türleri
Termodinamik incelemeler sonucunda enerjinin bir sistemin çevreyle etkileşimi sonucu
transfer olabileceği öğrendik. Bu etkileşimler “iş” ve “ısı” olarak isimlendirilmişti. Bununla
beraber termodinamik, bu etkileşimlerin tabiatı (mekanizmaları) ve hızlarıyla ilgilenmez.
Isı transferi, sıcaklık farklılığı nedeniyle termal (ısıl) enerjinin taşınımıdır. Bir ortamda ya da
ortamlar arasında ne zaman bir sıcaklık farklılığı (sıcaklık gradyenti) olursa, ısı transferi
gerçekleşir. Şekil 3.1 de ısı transfer türleri görülmektedir.
Şekil 3.1. Isı transfer türleri (kondüksiyon, konveksiyon, radyasyon)
Bir akışkan veya katı gibi sabit bir
ortamda, bir sıcaklık gradyenti olduğu
zaman, ortam boyunca gerçekleşen ısı
transferi türüne kondüksiyon denir.
Buna karşılık sıcaklıkları farklı olan
bir yüzey ile hareketli bir akışkan
arasında gerçekleşen ısı transfer
türüne konveksiyon adı verilir.
Üçüncü ısı transfer türü ise termal
(ısıl) radyasyon dur. Bütün yüzeyler
enerjiyi
elektromanyetik
dalga
formunda
dışarıya
vermektedir.
Böylece, bir ortamın olmadığı
durumda, farklı sıcaklıklardaki iki
yüzey arasında radyasyonla net bir ısı
transferi vardır.
Şekil 3.2. Isı transfer türleri
23
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
SORU (Kısa Sınav 1, 2014): Aşağıdaki şekilde verilen bir şöminede farklı bölgelerde gerçekleşen
ısı transfer türlerini tabloda yazınız. (Not: Bir olayda birden fazla ısı transferi gerçekleşebilir)
Cevap:
No
Isı transfer olayı
Isı transfer türü
1
Bacadan dışarıya havayla
Konveksiyon
2
Ateşten cama
Konveksiyon + Radyasyon
3
Çift cam arasında havayla
Konveksiyon
4
Cam içinden
Kondüksiyon
5
Şömine tuğlasından odaya
Konveksiyon + Radyasyon
6
Ateş haznesinin ayağından zemine
Kondüksiyon
Kondüksiyonla Isı İletimi
Isı transfer prosesleri için de hız denklemleri
vardır. Bu denklemler genel olarak birim
zamanda transfer edilen enerji miktarını
sunmaktadır. Kondüksiyonla ısı iletimi için
verilen hız denklemine Foruier Kanunu adı
verilmektedir. Şekil 3.3 de verilen, bir T(x)
sıcaklık dağılımına sahip bir duvarda hız
denklemi,
𝑞𝑥∗ = −𝑘
Şekil 3.3. Kondüksiyonla bir boyutlu ısı
transferi
𝑑𝑇
𝑑𝑥
(3-1)
Olup buradaki ısı akışı (q*, W/m2), transfer
edilen yöne dik olan birim alandan, x yönündeki
ısı transfer hızıdır ve bu yöndeki sıcaklık
gradyenti (dT/dx) ile orantılıdır. k parametresi ise
termal iletkenlik (W/m.K) olarak bilinir ve duvar
malzemesinin bir karakteristik özelliğidir. Eksi
işareti, ısının azalan sıcaklık yönünde transfer
edildiğinin bir ifadesidir.
24
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Sabit koşullar altında Şekil 3.3 deki duvarda sıcaklık dağılımı lineerdir, bu yüzden sıcaklık
gradyenti aşağıdaki gibi yazılabilir.
𝑑𝑇 𝑇2 − 𝑇1
=
𝑑𝑥
𝐿
Bu durumda ısı akışı,
𝑞𝑥∗ = −𝑘
veya
𝑞𝑥∗ = 𝑘
𝑇2 − 𝑇1
𝐿
𝑇1 − 𝑇2
∆𝑇
=𝑘
𝐿
𝐿
(3-2)
(3-3)
(3-4)
Örnek 3.2. Bir endüstriyel fırın
duvarı, termal iletkenliği 1.7
W/m.K olan ve 15 cm
kalınlığındaki bir ateş tuğlasıyla
örülüdür. Sabit hal operasyonu
ölçümlerinde fırının iç ve dış
duvar sıcaklıklarının sırasıyla
1400 K ve 1150 K olduğu tespit
edilmiştir. 50 cm yüksekliğinde
ve 1.2 m genişliğindeki duvar
içerisinden gerçekleşen ısı akış
hızını ve ısı kaybını bulunuz.
Çözüm.
𝑞𝑥∗ = 𝑘
∆𝑇
𝑊
1400 𝐾 − 1150 𝐾
= 1,7
𝑥
= 2833 𝑊/𝑚2
𝐿
𝑚. 𝐾
0,15 𝑚
Isı akışı (𝑞𝑥∗ ), birim alandan geçen ısı transfer hızıdır ve duvarın yüzeyi boyunca üniformdur
(değişmez). Bir A alanına sahip duvarda gerçekleşen ısı kaybı (𝑞𝑥 ) ise,
𝑞𝑥 = 𝐴. 𝑞𝑥∗ = (1,2 𝑚 𝑥 0,5 𝑚) 𝑥 2833 𝑊/𝑚2 = 1700 𝑊
Örnek 3.3. Levha şeklindeki bir izolasyon malzemesinin termal iletkenlik sabiti (katsayısı)
0.029 W/m.K dir. 20 mm kalınlığındaki bu izolasyon levhasında ölçülen sıcaklık farkı, T1T2=10°C olduğuna göre, 2m x 2m ebatlarındaki izaolasyon levhasındaki ısı akış hızını ve ısı
kaybını bulunuz.
Çözüm.
𝑞𝑥∗ = 𝑘
∆𝑇
𝑊
10°𝐶
= 0,029
(
) = 14,5 𝑊/𝑚2
𝐿
𝑚. 𝐾 0,02 𝑚
Dikkat: T1-T2=10°C (=10 K) dir. (30°C-20°C=10°C veya Kelvin cinsinden 303 K-293 K=10
K halinde fark aynı olacaktır.)
Alan = 2m x 2m = 4 m2
25
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑞𝑥 = 𝐴. 𝑞𝑥∗ = 4 𝑚2 𝑥 14,5
𝑊
= 58 𝑊
𝑚2
Örnek 3.4. 20 m2 lik bir alana ve 25 cm lik kalınlığa sahip bir beton duvar, soğutulan bir
odayla dış ortamı birbirinden ayırmaktadır. Duvarın iç yüzey sıcaklığı 25°C de sabit
tutulmaktadır. Beton termal iletkenlik katsayısı 1 W/m.K dir. Kış ve yaz mevsim şartlarındaki
en uç noktalar olan -15°C ve +38°C lik duvar dış yüzey sıcaklığı için ısı kayıplarını
hesaplayınız.
Çözüm.
Kış şartları için, T1 = 25°C ve T2 = -15°C
𝑞𝑥∗ = 𝑘
∆𝑇
25 − (−15)
40
𝑊
= 1𝑥
=
= 160 2
𝐿
0,25
0,25
𝑚
Isı kaybı, 𝑞𝑥 = 𝐴 𝑥 𝑞𝑥∗ = 20 𝑥 160 = 3200 𝑊
Yaz şartları için, T1 = 25°C ve T2 = 38°C
𝑞𝑥∗ = 𝑘
∆𝑇
25 − 38
𝑊
=1𝑥
= −52 2
𝐿
0,25
𝑚
Isı kaybı, 𝑞𝑥 = 𝐴 𝑥 𝑞𝑥∗ = 20 𝑥 (−52) = −1040 𝑊
Örnek 3.5. Ahşap ev yapımında kullanılan bir ağaç kütüğünün kalınlığı 50 mm, iç yüzey
sıcaklığı 40°C, dış yüzey sıcaklığı 20°C dir. Bu ağaç kütükten ısı akış hızı 40 W/m 2 olduğuna
göre ağacın termal iletkenlik katsayısını bulunuz.
Çözüm. 𝑞𝑥∗ = 𝑘
∆𝑇
𝐿
40 − 20
= 𝑘 𝑥 400
0,05
𝑊
𝑘 = 0,1
𝑚. 𝐾
40 = 𝑘
Örnek 3.6. Bir cam pencerenin kalınlığı 5 mm, iç ve dış yüzey sıcaklıkları sırasıyla 15 ve 5°C
dir. 1m x 3 m boyutlarındaki bu cam pencereden ısı kaybını bulunuz. Camın termal iletkenliği
1.4 W/m.K dir.
Çözüm.
𝑞𝑥∗ = 𝑘
∆𝑇
15 − 5
𝑊
= 1,4 𝑥
= 2800 2
𝐿
0,005
𝑚
Isı kaybı, 𝑞𝑥 = 𝐴 𝑥 𝑞𝑥∗ = 3 𝑥 2800 = 8400 𝑊
Örnek 3.7. 11 m uzunluğunda 8 m genişliğinde ve 20 cm kalınlığında bir beton zeminin kışın
üst yüzey sıcaklığı 17°C, alt yüzey sıcaklığı ise 10°C olarak ölçülmüştür. Betonun termal
26
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
iletkenliği 1.4 W/m.K olduğuna göre ısı kaybını bulunuz. Bu kaybın 1 saatte gerçekleştiğini
kabul ederek, odanın %88 verimle doğalgazla ısıtılması durumunda bir gün boyunca ısı
kaybının maliyeti ne kadar olacaktır. (Oda gün boyu ısıtılmaktadır ve doğalgazın maliyeti
1,75Kr/MJ )
Çözüm.
𝑞𝑥∗ = 𝑘
∆𝑇
17 − 10
𝑊
= 1,4 𝑥
= 49 2
𝐿
0,2
𝑚
Isı kaybı, 𝑞𝑥 = 𝐴 𝑥 𝑞𝑥∗ = (11𝑥8) 𝑥 49 = 4312 𝑊
Bu ısı kaybının 1 saatte gerçekleştiği kabul edilmiştir. JOULE = WATT x SANİYE çevrimine
göre bir günde 24x60x60= 86400 saniye olduğuna göre, %88 lik ısıtma verimi göz önüne
alındığında, bir günde gerçekleşecek ısı kaybını karşılamak üzere yapılan ısıtma miktarı,
𝐼𝑠𝚤𝑡𝑚𝑎 𝑚𝑖𝑘𝑡𝑎𝑟𝚤 (𝐽) =
4312 𝑊
𝑥86400 𝑠𝑛 = 423360000 𝐽 = 423,36 𝑀𝐽
0,88
Bir günlük ısıtma maliyeti,
𝐺ü𝑛𝑙ü𝑘 𝑚𝑎𝑙𝑖𝑦𝑒𝑡 = 423,36 𝑥 1,75 = 740 𝐾𝑟 = 7,40 𝑇𝐿
(aylık ısıtma maliyeti = 30 x 7,4 = 222 TL)
Problem (Ödev 3, 2014): Ahşap evler tuğladan yapılan evlere nazaran daha iyi ısı yalıtımına
sahiptir. Ahşaptan yapılmış 10 cm kalınlığındaki duvarın dış yüzey sıcaklığının 5°C olduğu
bir soğuk günde duvarın iç yüzey sıcaklığı 20°C olacak şekilde ev ısıtılmaktadır. Tuğladan
yapılmış bir evde aynı termal koşulların sağlanabilmesi için duvar kalınlığı kaç cm olmalıdır.
kahşap= 0,16 W/m.°C, ktuğla= 0,72 W/m.°C
Çözüm.
Ahşaptan yapılması durumunda,
𝑞=𝑘
∆𝑇
𝑊 (20 − 5)°𝐶
𝑊
= (0,16
)
= 24 2
𝐿
𝑚. °𝐶
0,1 𝑚
𝑚
Aynı koşullarda tuğla için,
𝑞=𝑘
24
∆𝑇
𝐿
𝑊
𝑊 (20 − 5)°𝐶
= (0,72
)
2
𝑚
𝑚. °𝐶
𝐿
𝐿 = 0,45 𝑚 = 45 𝑐𝑚
27
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Konveksiyonla Isı İletimi
Konveksiyonla ısı transferi, iki mekanizma içermektedir. Rasgele moleküler hareket
(difüzyon) nedeniyle gerçekleşen enerji transferine ilave olarak, enerji ayrıca akışkanın
hacimsel hareketi nedeniyle de transfer olur. Bu akışkan hareketi, çok sayıda molekülün
kolektif olarak (birlikte) veya kümeler halinde hareketi sayesinde gerçekleşir. Bir sıcaklık
gradyentinin olduğu durumda bu tür bir akışkan hareketi, ısı transferini sağlayacaktır.
Kümeler halindeki moleküllerin rasgele hareketleri kaybolduğu için, toplam ısı transferi,
akışkanın hacimsel hareketi ile moleküllerin rasgele hareketinin birlikte gerçekleşmesi
durumuyla sağlanmaktadır. Gerçekte hacimsel taşınıma “adveksiyon” denmektedir.
Konveksiyon ise moleküler taşınımdır fakat hem moleküler hem de hacimsel taşınıma genel
olarak konveksiyon terimi kullanılmaktadır.
Konveksiyonla ısı transferinde, özellikle iki farklı sıcaklıklara sahip olduklarında, bir yüzey
ile hareket halindeki bir akışkan arasındaki ısı transferiyle ilgileneceğiz. Şekil 3.4 de ısıtılan
bir yüzey üzerinde akan bir akışkanı ele alalım. Yüzeyle akışkanın etkileşimi sonucunda,
yüzeyde akışkan hızının sıfır olduğu bir bölge oluşacaktır. Akışkanın bu bölgesine
hidrodinamik sınır tabakası veya kısaca sınır tabakası adı verilmektedir. Yüzey ve akışkan
sıcaklıkları farklı olduklarında, sıcaklığın y=0 da Ts den akışkanın dış tarafındaki T∞ değerine
kadar değişen bir akışkan bölgesi olacaktır. Bu bölgeye de termal sınır tabakası adı verilir ki
bu bölge hızın değişimine bağlı olarak küçük veya büyük bir bölge olabilir. Eğer Ts>T∞ ise,
bu durumda konveksiyonla ısı transferi, yüzeyden akışkanın dış kısmına doğru
gerçekleşecektir.
Şekil 3.4. Konveksiyonla ısı transferinde sınır tabakası gelişimi
Akışkan hızının sıfır olduğu yüzeye yakın bölgede rasgele meloküler hareket gerçekleşir,
burada akışkanın hacimsel hareketi yoktur. Gerçekte akışkanla yüzey arasındaki arayüzeyde
akışkanın hızı sıfırdır ve ısı da sadece bu mekanizmayla transfer olur. Akma olayı x-yönünde
gerçekleştikçe sınır tabakası büyür. Bu tabakadaki ısı akma yönüne doğru iletilir (süpürülür),
sınır tabakasının dışına, akışkana doğru transfer olur.
Konveksiyonla ısı transferi, akmanın tabiatına bağlı olarak sınıflandırılabilir. Akma olayı bir
fan, bir pompa veya atmosferik rüzgarlar gibi dış yardımlarla yapıldığı zaman, kuvvetli
konveksiyon veya kuvvetli akma şeklinde isimlendirilir. Örnek olarak, Şekil 3.5(a) daki bir
elektronik baskı devresindeki ısınan bileşenlerin soğutulması bu şekilde gerçekleştirilmekte,
28
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
buna karşılık Şekil 3.5(b) deki soğutma, serbest konveksiyon (veya doğal konveksiyon) ile
sağlanmaktadır. Doğal konveksiyonda akma olayı “buoyancy kuvvetleri” ile (Bakınız Şekil
3.6) sağlanmakta olup bu kuvvetler, akışkandaki farklı sıcaklık bölgeleri nedeniyle farklı
viskoziteye sahip bölgelerin oluşması nedeniyle gerçekleşmektedir.
Şekil 3.5. Konveksiyon ısı transfer prosesleri (a) kuvvetli konveksiyon, (b) doğal
konveksiyon, (c) kaynama, (d) yoğunlaşma
Şekil 3.6. Doğal konveksiyonda buoyancy kuvvetleriyle ısı taşınımına örnekler
Şekil 3.5(a) da sadece kuvvetli konveksiyon, Şekil 3.5(b) de ise sadece doğal konveksiyon
görülmektedir. Oysa her ikisinin de birlikte olduğu koşullar vardır. Konveksiyon ısı transferi,
kondüksiyon ve hacimsel hareketin birlikte etkileriyle bir akışkanda gerçekleşen enerji
transferi olarak tarif edilmiştir. Transfer edilen enerji, akışkanın termal enerjisidir. Bununla
birlikte ısı değişimlerinin olduğu konveksiyon prosesleri de vardır. Isı değişimi, akışkanın sıvı
ve buhar fazları arasında bir faz değişimiyle gerçekleşmektedir. Bu duruma iki örnek,
kaynama ve yoğunlaşmadır. Örneğin konveksiyon ısı transferi, Şekil 3.5(c) deki gibi
kaynayan bir suyun dip kısmında oluşan kabarcıklarla sağlanan akışkan hareketiyle veya Şekil
3.5(d) deki gibi soğuk bir borunun dış yüzeyinde su buharının yoğunlaşması verilebilir.
29
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Konveksiyonla ısı transferinde denklem,
𝑞 ∗ = ℎ(𝑇𝑠 − 𝑇∞ )
Şeklinde olup burada q* konvektiv ısı akışı (W/m2), h parametresi ise konveksiyon ısı transfer
sabitidir (W/m2.K). Ts ve T∞ ise sırasıyla yüzey ve akışkan sıcaklıklarıdır. “h” parametresi
yüzey geometrisinden, akışkanın tabiatından etkilenen sınır tabakasındaki koşullara bağlıdır.
Denklem (xxx) kullanıldığında, ısı yüzeyden transfer olduğunda ( Ts > T∞ ) konvektif ısı akışı
pozitif, ısı yüzeye doğru transfer oluyorsa ( Ts < T∞ ) negatif olacaktır. Konveksiyon ısı
transfer katsayısının tipik değerleri Tablo 3.1 de verilmiştir.
Tablo 3.1. Tipik konveksiyon ısı transfer sabitleri
Proses
Serbest konveksiyon
Gazlar
Sıvılar
Kuvvetli konveksiyon
Gazlar
Sıvılar
Faz değişimli konveksiyon
Kaynama ve Yoğunlaşma
h (W/m2.K)
2 – 25
50 – 1000
25 – 250
100 – 20000
2500 – 100000
Problem (Ödev 4, 2014): 3 W’lık bir güç transistörü 10 mm yüksekliğinde ve 12 mm
çapındadır. Bu transistörün yüzey sıcaklığının maksimum 85°C ye çıkmasına izin
verilmektedir. Soğutma amacıyla gönderilen havanın konveksiyon ısı katsayısı 100 W/m 2K
olduğuna göre transistörün bozulmaması için gönderilen havanın sıcaklığı ne olmalıdır?
Çözüm.
Transistörün yüzey alanı (A) = (2πr.L)+πr2 = (2x3,14x6x10)+(3,14x62) = 376,8+113,04
A = 489,84 mm2 = 4,9.10-4 m2
𝑞 = ℎ𝐴(𝑇𝑠 − 𝑇∞ )
𝑇∞ = 𝑇𝑠 −
𝑞
3
= 85 −
= 85 − 61,2 = 23,8°𝐶
ℎ𝐴
100 𝑥 4,9. 10−4
30
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Radyasyonla Isı İletimi
Termal radyasyon, madde tarafından yayılan enerjidir. Her ne kadar katı maddelerden
gerçekleşen radyasyona odaklanacak olsak da, bu tür emisyonlar (yayma) gazlar ve sıvılardan
da gerçekleşmektedir. Maddenin formuna bakılmaksızın emisyonlar, atom ve moleküllerin
elektron düzenindeki değişimlere bağlanmaktadır. Kondüksiyon ve konveksiyonla enerji
transferi bir ortamın varlığına ihtiyaç duyar, oysa radyasyon ihtiyaç duymaz. Gerçekte
radyasyon transferi en etkin şekilde vakum ortamında gerçekleşir.
Şekil 3.7(a) da verilen radyasyon transfer prosesini göz önüne alalım. Yüzeyler tarafından
yayılan radyasyon, yüzeye yakın bağ yapmış maddenin termal enerjisinden kaynaklanmakta
olup enerjinin birim alandaki yayınım hızı (W/m2), Yüzey Yayınım Gücü (E) olarak
isimlendirilmektedir. Yayınım gücünün bir üst limiti olup Stefan – Boltzman Kanunu ile
verilmektedir.
𝐸𝑏 = 𝜎 𝑇𝑠4
Bu denklemde Ts yüzey sıcaklığı (K), σ ise Stefan – Boltzman sabitidir (5,67.10-8 W/m2.K4).
Bu üst sınırdan yayma gücüne sahip böyle bir yüzeye ideal radyatör veya blackbody adı
verilmektedir.
Gerçek bir yüzey tarafından yayılan ısı akışı, aynı sıcaklıktaki bir blackbody’den daha azdır
ve denklemi aşağıdaki şekilde verilir.
𝐸 = 𝜎 𝜀 𝑇𝑠4
Bu denklemdeki ε, “emisivite” olarak adlandırılan, yüzeyin radyatif özelliğidir. 0 ≤ ε ≤ 1
aralığındaki değerlere sahiptir ve bu özellik, blackbody’ye oranla bir yüzeyin enerjiyi hangi
verimle yayacağının bir ölçüsüdür. Bu değer aynı zamanda malzemenin yüzey özelliklerine
de (yüzey pürüzlülüğü gibi) kuvvetli şekilde bağlıdır.
Şekil 3.7. Radyasyon değişimi. (a) bir yüzeyde, (b) bir yüzeyle geniş çevre arasında.
Radyasyon çevreden bir yüzey üzerine doğru olarak ta gerçekleşebilir, güneş gibi özel bir
kaynaktan da gelebilir. Geldiği kaynaklara bakılmaksızın bir yüzeyin birim alanına doğru olan
31
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
bu tür bir radyasyon hızı, aydınlanma (G) olarak isimlendirilir (Bkz. Şekil 3.7a). Bir kısım
veya bütün bir aydınlanma, yüzey tarafından absorbe (soğurma, emme) edilebilir, bunun
sonucunda da malzemedeki termal enerjide artış meydana gelmektedir. Birim alanda absorbe
edilen enerji hızı, absortivite (α) olarak adlandırılmaktadır.
𝐺𝑎𝑏𝑠 = 𝛼 𝐺
α değeri 0 ≤ α ≤ 1 arasındadır. α < 1 olduğunda yüzey opaktır, bir kısım aydınlanma
yansımaktadır. Yüzey yarı-transparan ise bir kısım aydınlanma yayınabilir (malzeme içinden
geçebilir). Ancak absorbe edilen ya da yayılan radyasyon, malzemenin termal enerjisini
arttıracağı veya azaltacağı için, yansıtılan veya geçirimine izin verilen radyasyonun,
malzemenin termal enerjisine bir etkisi yoktur.
α değeri, yüzeyin özelliğiyle birlikte
aydınlanma durumuna da bağlıdır. Örneğin bir yüzeyin güneşten gelen radyasyona olan
absortivitesi, bir fırının duvarından yayılan radyasyona olan absortivitesinden farklıdır. Yani
bir yüzeyin absortivitesi, farklı radyasyon kaynaklarına göre farklılık göstermektedir.
Birçok mühendislik probleminde radyasyon ısı transferine karşı sıvıların opak, gazların ise
transparan olduğu kabul edilmiştir. Katılar metallerde olduğu opak olabilirler veya bazı ince
polimerik ve yarıiletken levhalardaki gibi yarı-transparan olabilirler.
Şekil 3.7(b)’de gösterildiği gibi, Ts yüzey sıcaklığındaki küçük bir yüzeyle bu yüzeyi
çevreleyen sabit sıcaklıktaki geniş bir yüzey (çevre) arasındaki radyasyon değişiminin olduğu
özel bir durumu ele alalım. Çevreye örnek olarak alt yüzeyden farklı sıcaklıktaki bir fırının
veya odanın duvarları olabilir. Böyle bir koşulda aydınlanma, Tçevre sıcaklığındaki bir
blackbody’den gerçekleşen yayınıma eşit olabilir ve bu durumda,
4
𝐺 = 𝜎 𝑇ç𝑒𝑣𝑟𝑒
geçerlidir. α = ε durumunda (gri yüzey), birim yüzey alanından gerçekleşen net radyasyon
hızı aşağıdaki denklemle tespit edilir.
𝑞
4
𝑞 ∗ = 𝐴 = 𝜀 𝐸𝑏 𝑇𝑠 − 𝛼 𝐺 = 𝜀 𝜎 (𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
)
Bu denklem, radyasyon yayınımıyla ortaya çıkan termal enerji ile radyasyon absorbsiyonuyla
elde edilen termal enerji arasındaki farkı ortaya koymaktadır.
Net radyasyon ısı değişimini veren denklem,
𝑞𝑟𝑎𝑑 = ℎ𝑟 𝐴 (𝑇𝑠 − 𝑇ç𝑒𝑣𝑟𝑒 )
olup burada hr, radyasyonla ısı transfer sabiti’dir.
2
ℎ𝑟 ≡ 𝜀 𝜎 (𝑇𝑠 + 𝑇ç𝑒𝑣𝑟𝑒 )(𝑇𝑠2 + 𝑇ç𝑒𝑣𝑟𝑒
)
Radyasyonla ısı transfer sabiti (hr) terimi sıcaklığa kuvvetli şekilde bağlıdır, buna karşılık
konveksiyonla ısı transfer sabiti (h) sıcaklığa çok zayıf bağlıdır. Şekil 3.7 de yüzeyden hem
radyasyonla hem de konveksiyonla ısı transferi söz konusudur. Bu durumda toplam ısı
transfer hızı aşağıdaki denklemle hesaplanmaktadır.
4
𝑞 = 𝑞𝑘𝑜𝑛𝑣 + 𝑞𝑟𝑎𝑑 = ℎ 𝐴 (𝑇𝑠 − 𝑇∞ ) + 𝜀 𝐴 𝜎 (𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
)
32
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Örnek 3.8. İzole edilmemiş ve içinden buhar geçen bir boru, duvarları ve içerideki havası
25oC olan bir odadan geçmektedir. Borunun dış çapı 70 mm, iç yüzey sıcaklığı 200oC,
borunun emisivitesi 0.8 dir. Yüzey emisyon gücü ve aydınlanma nedir? Yüzeyden havaya
serbest konveksiyonla ısı transferiyle ilgili sabit 15 W/m2K ise borunun birim uzunluğunda,
yüzeyden gerçekleşen ısı kaybı hızı nedir ?
Çözüm:
𝐸 = 𝜀 𝜎 𝑇𝑠4 = 0,8 (5,67. 10−8
4
𝐺 = 𝜎 𝑇ç𝑒𝑣𝑟𝑒
= 5,67. 10−8
𝑊
𝑊
4
(473
)
𝐾)
=
2270
𝑚2 𝐾 4
𝑚2
𝑊
𝑊
(298 𝐾)4 = 447 2
2
4
𝑚 𝐾
𝑚
4
𝑞 = 𝑞𝑘𝑜𝑛𝑣 + 𝑞𝑟𝑎𝑑 = ℎ𝐴(𝑇𝑠 − 𝑇∞ ) + 𝜀𝐴𝜎 (𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
)
𝑞 = (15
𝑊
) (𝜋. 0,07 𝑚)(473 𝐾 − 298 𝐾)
𝑚2 𝐾
+ 0,8(𝜋. 0,07 𝑚) (5,67. 10−8
𝑞 = 577
𝑊
) (4734 − 2984 )𝐾 4
𝑚2 𝐾 4
𝑊
𝑊
𝑊
+ 421
= 998
𝑚
𝑚
𝑚
Problem 3.9. İçerisinde sıcak kahve bulunan bir termos, havası ve duvarları aynı sabit
sıcaklıkta bulunan bir odada bulunmaktadır. Farklı kademelerde gerçekleşen ısı transfer
türlerini belirtiniz.
Çözüm:
Isı transfer
kademesi
q1
q2
q3
q4
q5
q6
q7
q8
Isı transfer türü
Konveksiyon
Kondüksiyon
Konveksiyon
Konveksiyon
Radyasyon
Kondüksiyon
Konveksiyon
Radyasyon
Nereden nereye
Sıcak kahveden plastik şişeye
Şişe içinden
Şişeden havaya
Havadan dış kaba
Şişenin dış yüzeyinden dış kaba
Dış kap içerisinden
Dış kap yüzeyinden odadaki havaya
Dış kap yüzeyinden oda duvarı yüzeyine
33
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem 3.10. Elinizi hareket eden bir araçtan dışarı çıkardığınızda ya da akan bir suya
daldırdığınızda, konveksiyonla ısı iletimi durumuyla karşılaştınız demektir. Elinizin yüzey
sıcaklığı 30°C olduğunda,
a) 35 km/h hızla giden bir araçta iken, dışarısı -5°C de ve konveksiyon sabiti 40
W/m2.K olan hava olduğunda konvektiv ısı akışını bulunuz.
b) Konveksiyon sabiti 900 W/m2.K, sıcaklığı 10°C olan ve 0.2 m/sn hızında akan bir
sudaki konvektiv ısı akışını bulunuz.
c) Yukarıdaki koşullardan hangisi daha soğuk hissettirir? Bu sonuçları normal oda
koşullarında ve yaklaşık 30 W/m2 lik ısı kaybıyla karşılaştırınız.
Çözüm:
El yüzeyinde sıcaklık üniformdur, konveksiyon sabiti de el üzerinde üniformdur. Su ve
havanın akan (hareketli) durumda olması nedeniyle radyasyonla ısı değişimi ihmal edilebilir.
a) Hava akımı için;
b) Akan su için;
𝑊
𝑞 ∗ = ℎ(𝑇𝑠 − 𝑇∞ ) = 40 𝑚2 𝐾 [30 − (−5)]𝐾 = 1400
𝑊
𝑞 ∗ = ℎ(𝑇𝑠 − 𝑇∞ ) = 900 𝑚2 𝐾 [30 − 10]𝐾 = 18000
𝑊
𝑚2
𝑊
𝑚2
c) Akan su içindeki ısı kaybı, daha soğuk olan havadaki duruma göre daha fazla olmaktadır.
Bu nedenle 10°C lik akan suya daldırılan elde soğukluğu daha fazla hissederiz. Buna karşılık
30 W/m2 lik ısı kaybının olduğu bir odada, yukarıdaki koşullarla karşılaştırdığımızda
kendimizi çok daha rahat hissederiz.
Problem 3.11. Bir elektrikli direnç ısıtıcısı, 30 mm çapındaki uzun bir silindire
yerleştirilmiştir. Silindir içinden 25°C de ve 1 m/sn hızında su geçtiğinde, yüzeyi 90°C de
tutmak için gerekli birim uzunluk başına güç 28 kW/m dir. Yine 25°C de ve 10 m/sn hızında
hava kullanıldığında gerekli değer 400 W/m dir. Su ve hava akışları için konveksiyon
sabitlerini hesaplayın ve karşılaştırın.
Çözüm:
34
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑞 ∗ = ℎ. 𝐴. (𝑇𝑠 − 𝑇∞ ) = ℎ. (𝜋𝐷). (𝑇𝑠 − 𝑇∞ )
Alan hesaplamasındaki işlem birim uzunluk içindir. Buradaki konveksiyon sabiti (h);
ℎ=
Su için;
ℎ=
Hava için;
𝑞∗
(𝜋𝐷)(𝑇𝑠 − 𝑇∞ )
28000
𝑊
= 4570 2
𝜋. 0,03. (90 − 25)
𝑚 𝐾
ℎ=
400
𝑊
= 65 2
𝜋. 0,03. (90 − 25)
𝑚 𝐾
Suyun konveksiyon katsayısı, havanın konveksiyon katsayısının yaklaşık 70 katıdır. Suyun
konveksiyon yoluyla ısı iletimi havaya göre daha fazladır.
Problem 3.12. Bir elektrikli ısıtıcı 200 mm uzunluğunda ve 20 mm dış çapında silindirik
şekillidir. Normal çalışma koşullarında bu ısıtıcı, 20°C sıcaklığındaki akan bir suya
daldırıldığı zaman 2 kW ısı vermektedir. Konveksiyon sabiti 5000 W/m2.K dır. Isıtıcının
yüzey sıcaklığını bulunuz.
Çözüm.
𝑃 = 𝑞𝑘𝑜𝑛𝑣 = ℎ. 𝐴. (𝑇𝑠 − 𝑇∞ ) = ℎ. (𝜋𝐷𝐿)(𝑇𝑠 − 𝑇∞ )
𝑇𝑠 = 𝑇∞ +
𝑞
2000 𝑊
= 20°𝐶 +
= 20°𝐶 + 31,8°𝐶 = 51,8°𝐶
𝑊
ℎ𝜋𝐷𝐿
5000 2 (𝜋. 0,02 𝑚. 0,2 𝑚)
𝑚 𝐾
Problem 3.13. Bir ısıtma-soğutma sistemi ile aynı oda sıcaklığının sağlandığı koşullarda, bir
kişinin kışın farklı yazın farklı hissetmesi olağan bir durumdur. Bu durumu hesaplama
yaparak izah ediniz. Odanın sıcaklığı yaz – kış 20°C olarak kabul edilsin, odanın duvarları
yazın 27°C, kışın ise 14°C olsun. Yıl boyunca bu kişinin sıcaklığı 32°C, emisivitesi 0.9, kişi
ile odanın havası arasındaki doğal konveksiyonla oluşan ısı transfer katsayısı yaklaşık 2
W/m2.K dir.
35
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Çözüm:
Yaz ve kış oda sıcaklığı sabitlendiği için konveksiyonla ısı transferi değişmeyecektir.
∗
𝑞𝑘𝑜𝑛𝑣
= ℎ. (𝑇𝑠 − 𝑇∞ ) = 2
𝑊
𝑊
(32 − 20) 𝐾 = 24 2
2
𝑚 𝐾
𝑚
Buna karşılık radyasyona bağlı ısı kaybı farklı olacaktır.
𝑊
Yazın:
∗
4
𝑞𝑟𝑎𝑑
= 𝜀 𝜎 (𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
) = 0,9 𝑥 5,67. 10−8 𝑥(3054 − 3004 ) = 28,3
𝑚2
Kışın:
∗
4
𝑞𝑟𝑎𝑑
= 𝜀 𝜎 (𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
) = 0,9 𝑥 5,67. 10−8 𝑥(3054 − 2874 ) = 95,4
𝑚2
𝑊
Görüldüğü gibi konveksiyon yoluyla ısı kaybı aynı olmasına karşılık, radyasyon yoluyla ısı
kaybı kışın daha fazladır.
Problem 3.14. 25 m uzunluğunda, 100 mm çapında ve izole edilmemiş bir endüstriyel
borunun içerisinden basınçlı buhar geçmekte ve borunun dış yüzeyini 150°C de sabit
tutmaktadır. Bu boru, duvarları ve havası 25°C olan bir odadan geçmektedir. Doğal
konveksiyon sabiti 10 W/m2.K, yüzey emisivitesi 0,8 olduğuna göre borudan gerçekleşen ısı
kaybını bulunuz.
Çözüm:
4
𝑞 = 𝑞𝑘𝑜𝑛𝑣 + 𝑞𝑟𝑎𝑑 = 𝐴 [ℎ (𝑇𝑠 − 𝑇∞ ) + 𝜀 𝜎 (𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
)]
𝑞 = [𝜋 (0,1𝑚 𝑥 25𝑚)]𝑥[10 (150 − 25) + 0,8 𝑥 5,67. 10−8 (4234 − 2984 )]
𝑞 = 7,85 𝑚2 (1250 + 1095)
𝑊
= 18405 𝑊
𝑚2
36
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem 3.15. Bir levha, yüzeyi 650°C lik
(923 K) bir kaynaktan radyasyon almakta,
yüzeyi 150°C (423 K) olan bir kaynağa da
radyasyon vermektedir. Konveksiyon ısı
akışını ihmal ederek ve ε=1 kabul ederek,
ortada yer alan levhanın yüzey sıcaklığını
bulunuz.
Çözüm: Enerji korunumu gereği her iki
bölgede radyasyon olayı birbirine eşit
olacaktır.
𝜀 𝜎 𝐴 [𝑇14 − 𝑇 4 ] = 𝜀 𝜎 𝐴 [𝑇 4 − 𝑇24 ]
[9234 − 𝑇 4 ] = [𝑇 4 − 4234 ]
9234 + 4234 = 2 𝑇 4
4 9234 + 4234
𝑇=√
= 784.5 𝐾 (511.5°𝐶)
2
Problem (Ödev 5, 2014): Küp şeklindeki bir dişli kutusuna motordan 150 hp güç iletilmekte,
dişli sistemi %93 verimle çalışmaktadır (%7 si ısı kaybı). Bir kenarı 30 cm ve emisivite değeri
0,8 olan bu dişli kutusunun bulunduğu ortamda çevrenin sıcaklığı 30°C, dişli kutusundan
konveksiyon yoluyla gerçekleşen ısı kaybı 7560 W dır. Dişli kutusunun yüzey sıcaklığını
bulunuz. (1 hp = 746 W)
Çözüm.
Dişli kutusunun verdiği ısı = (150 x 746) x 0,07 = 7833 W
4
𝑃 = 𝑞𝑘𝑜𝑛𝑣 + 𝑞𝑟𝑎𝑑 = ℎ𝐴[𝑇𝑠 − 𝑇∞ ] + 𝜀𝐴𝜎[𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
]
7833 = 7560 + 0,8𝑥0,54𝑥5,67. 10−8 [𝑇𝑠4 − 3034 ]
𝑇𝑠4 − 8428892481 = 111,454. 108
𝑇𝑠4 = 19574292481
𝑇𝑠 = 374 𝐾 (101°𝐶)
Problem (Kısa Sınav 1, 2014): (1.Öğretim) Küp şeklindeki bir dişli kutusuna motordan 150
hp güç iletilmekte, dişli sistemi % 85 verimle çalışmaktadır (%15’i ısı kaybı). Bir kenarı 30
cm ve emisivite değeri 0,87 olan bu dişli kutusunun bulunduğu ortamda çevrenin sıcaklığı
30°C, dişli kutusundan konveksiyon yoluyla gerçekleşen ısı kaybı 7600 W dır. (1 hp=746 W,
σ = 5,67.10-8 W/m2K4)
a) Dişli kutusunun yüzey sıcaklığını bulunuz.
37
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
b) Dişli kutusunun bulunduğu ortamdaki havanın sıcaklığı 25°C kabul edilirse havanın
konvektif ısı iletim katsayısını bulunuz.
Çözüm.
(a)
Dişli kutusunun verdiği ısı = (150 x 746) x 0,15 = 16785 W
4
𝑃 = 𝑞𝑘𝑜𝑛𝑣 + 𝑞𝑟𝑎𝑑 = ℎ𝐴[𝑇𝑠 − 𝑇∞ ] + 𝜀𝐴𝜎[𝑇𝑠4 − 𝑇ç𝑒𝑣𝑟𝑒
]
16785 = 7600 + 0,87𝑥0,54𝑥5,67. 10−8 [𝑇𝑠4 − 3034 ]
𝑇𝑠4 − 8428892481 = 3,448. 1011
𝑇𝑠4 = 3,532. 1011
𝑇𝑠 = 771 𝐾 (498°𝐶)
(b)
𝑞𝑘𝑜𝑛𝑣 = ℎ 𝐴 [𝑇𝑠 − 𝑇∞ ]
7600 = h x 0,54 x [771 − 298]
7600
𝒉 = 255,42 = 29,75 W/m2.K
Problem (Kısa Sınav 1, 2014): (2.Öğretim)
1200 W’lık bir ütünün metalik tabanı 300 cm2’lik
alana sahiptir. Mevcut ısı ütü tabanından 25°C
sıcaklığa sahip ortam ve çevreye yayılmaktadır.
a) Metalik tabandan ısı transfer hızını (W/m2)
bulunuz.
b) Radyasyon ihmal edildiğinde, havanın
konvektif ısı iletim katsayısı 80 W/m2.K olması
durumunda ütü tabanının yüzey sıcaklığını,
c) Radyasyon dahil edildiğinde havanın yeni
konvektif ısı iletim katsayısını bulunuz.
(ε=0,95; σ = 5,67.10-8 W/m2K4)
Çözüm.
1200 𝑊
𝑊
(a)
𝑞 ∗ = 0,03 𝑚2 = 40000
(b)
𝑞𝑘𝑜𝑛𝑑ü𝑘𝑠𝑖𝑦𝑜𝑛 = 𝑞𝑘𝑜𝑛𝑣𝑒𝑘𝑠𝑖𝑦𝑜𝑛
𝑚2
𝑞𝑘𝑜𝑛𝑣 = ℎ 𝐴 [𝑇𝑠 − 𝑇∞ ]
38
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
1200 = 80 . 0,03 . [𝑇𝑠 − 25]
𝑇𝑠 = 25 +
1200
2,4
= 25 + 500 = 525°𝐶 (798 𝐾)
𝑞 = 𝑞𝑘𝑜𝑛𝑣 + 𝑞𝑟𝑎𝑑
(c)
1200 = ℎ. 0,03. [798 − 298] + 0,95 . 0,03 . 5,67. 10−8 [7984 − 2984 ]
1200 = 15. ℎ + 642,5
ℎ=
1200−642,5
15
= 37,2
𝑊
𝑚2 𝐾
Termal iletkenlik
Termal iletkenlik sabiti ısı transferinde önemli bir rol oynar. Elektriksel iletkenliği iyi olan
malzemelerin termal iletkenliği de iyidir. Metaller iyi termal iletkendir. Daha sonra alaşımlar
gelir. Sıvıların iletkenliği bu malzemelerden daha azdır. Gazların ise en düşüktür.
Katılarda ısı iletimi iki yolla gerçekleşir;
a) termal olarak aktive olan elektronların hareketi
b) termal olarak aktive olmuş elektronların aktifliği sayesinde oluşan latis dalgalanmaları
İletken malzemelerde etkin olan elektron
akışıdır. Alaşımlarda ise her iki yolla ısı
iletimi olur. Yalıtkanlarda latis dalgalanması etkindir. Sıvılarda kondüksiyon
olayı atomik ve moleküler difüzyonla
gerçekleşirken gazlarda ise kondüksiyon
olayı moleküllerin yüksek enerji seviyelerinden düşük enerji seviyelerine difüzyonuyla gerçekleşmektedir. Termal iletkenlik olayı, sıcaklıktaki değişim sayesinde gerçekleşir. Elektriksel iletkenliği
iyi olan malzemelerde sıcaklığın artmasıyla termal iletkenlik azalır, bunun
nedeni yüksek elektron yoğunluklarında
elektron akışının zorlaşmasıdır. Yalıtkan
malzemelerde ise sıcaklığın artması ile
termal atomik aktivite artacağı için
termal iletkenlik de artar. Gazlarda,
sıcaklığın artması ile atom ve moleküllerin artan hareketlenmesi nedeniyle
termal iletkenlik artar. Tablo 3.2 de bazı
malzemelerin termal iletkenlik katsayıları verilmiştir. Çeşitli malzemelerin
sıcaklığa bağlı olarak termal iletkenliğindeki değişim ise Şekil 3.8 de
verilmiştir
Şekil 3.8. Bazı malzemelerin termal iletkenlik
katsayılarının sıcaklıkla ilişkisi
39
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Tablo 3.2. Bazı malzemelerin 293 K deki (20oC) termal iletkenlikleri
Malzeme
Bakır
Aluminyum
Karbon çeliği (%1 C)
Krom çeliği (%20 Cr)
Krom-Nikel çeliği
Termal iletkenlik
katsayısı (W/mK)
386
204.2
43.3
22.5
12.8
Malzeme
Beton
Cam
Su
Hava
Termal iletkenlik
katsayısı (W/mK)
1.13
0.67
0.60
0.026
Birçok durumda ısı enerjisinin kaybını önlemek için cihazlar veya aparatlar izole edilirler. Bu
izolasyon malzemelerinin termal iletkenlik katsayıları düşük olmalıdır. Genel olarak üç tür
izolasyon malzemesi bulunmaktadır;
a) Fiber : küçük partiküller, izole edilecek
yüzeylerin arasındaki boşluğa doldurulurlar.
Mineral yünü (cam yünü de denir) bu tür bir
malzemedir. Yüksek sıcaklıklarda alumina ve
silika kullanılır.
b) Gözenekli : İçerisinde boşluklar oluşturulmuş,
poliüretan veya polisitren köpük olup
şekillendirilmiş parçalardır.
c) Granüler : Küçük inorganik tane veya
parçalardan oluşmuş yalıtım malzemesi olup
şekillendirilmiş halde veya toz halinde
kullanılır.(yandaki örnek : perlit)
Şekil 3.9. İzolasyon malzemeleri
Termal Difüzivite
Kondüksiyonla ısı iletiminde malzemenin bir diğer özelliği Termal Difüzivite’dir. Isı
kapasitesi bir malzemenin ısı depolama kabiliyetidir. Buna karşılık termal difüzivite (α), bir
malzeme içerisinden ısının ne kadar hızda (zaman açısından) difüze olmasını sunar.
40
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
İ𝑙𝑒𝑡𝑖𝑙𝑒𝑛 𝚤𝑠𝚤
𝑚2
𝑘
𝑇𝑒𝑟𝑚𝑎𝑙 𝐷𝑖𝑓ü𝑧𝑖𝑣𝑖𝑡𝑒 (𝛼) = 𝐷𝑒𝑝𝑜𝑙𝑎𝑛𝑚𝚤ş 𝚤𝑠𝚤 = 𝜌 𝐶 (𝑠𝑎𝑛𝑖𝑦𝑒)
(3-14)
𝑝
Termal iletkenlik (k) bir malzemenin ne kadar iyi iletken olup olmadığını, ısı kapasitesi (ρCp)
birim hacimde ne kadar enerji (ısı) depoladığını gösterir. Bu nedenle bir malzemenin termal
difüzivitesi, malzeme içerisinden iletilen ısının, birim hacimde depolanmış ısıya oranı olarak
ta verilebilir. Yüksek termal iletkenliğe veya düşük ısı kapasitesine sahip bir malzeme, büyük
bir termal difüziviteye sahiptir. Daha büyük termal difüzivite, ısının daha hızlı ilerlemesi
demektir. Küçük termal difüzivite değeri, ısının çoğunun malzeme tarafından absorblandığını,
çok küçük bir miktarının iletildiğini göstermektedir. Bazı malzemelerin termal difüziviteleri
Tablo 3.3 de verilmiştir.
Tablo 3.3. Bazı malzemelerin oda sıcaklığındaki termal difüziviteleri
Termal difüzivite (m2/sn)
149 x10-6
127 x10-6
113 x10-6
97.5 x10-6
22.8 x10-6
4.7 x10-6
1.2 x10-6
0.75 x10-6
0.52 x10-6
0.34 x10-6
0.23 x10-6
0.14 x10-6
0.14 x10-6
0.13 x10-6
Malzeme
Gümüş
Altın
Bakır
Aluminyum
Demir
Cıva
Mermer
Beton
Tuğla
Cam
Cam yünü
Su
Et
Ağaç (meşe)
Problem (Vize, 2014): 3 mm kalınlığında levha şeklinde imal edilmiş bir izolasyon
malzemesinin iki yüzü arasındaki sıcaklık farkı 100 K olduğundan gerçekleşen ısı akışı 8
kW/m2 dir. Bu malzemenin termal iletkenlik katsayısını ve termal difüzivite değerini bulunuz.
(izolasyon malzemesi için yoğunluk 30 kg/m3 ve ısı kapasitesi 1,5 kJ/kg.K)
Çözüm.
𝑞∗ = 𝑘
𝑘=
∝=
𝑘
𝜌 𝐶𝑝
=
𝑞∗ 𝐿
∆𝑇
0,24
30
𝑘𝑔
𝑚3
=
𝑊
𝑚.𝐾
𝑥 1,5
8000
𝑘𝑗
𝑘𝑔.𝐾
𝑊
𝑚2
∆𝑇
𝐿
𝑥 0,003 𝑚
100 𝐾
=
0,24
30
𝑘𝑔
𝑚3
= 0,24
𝐽
𝑚.𝑠.𝐾
𝑥 1500
𝐽
𝑘𝑔.𝐾
𝑊
𝑚.𝐾
= 5,33. 10−6
𝑚2
𝑠
41
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Sıcaklık Dağılımı
Bir duvardaki sıcaklık dağılımı, uygun sınır şartları kullanılarak çözülebilir. Şekil 3.10 da bir
duvar içerisinden tek yönlü (x yönü) ısı transferine bağlı sıcaklık dağılımı görülmektedir.
Sıcak akışkandan duvara konveksiyon, duvar içinde kondüksiyon ve duvarın dış yüzeyinden
konveksiyonla ısı transferi gerçekleşmektedir. Her bir kademe elektrik direnci şeklinde
sembolize edilmiştir. Bu durumda kondüksiyondaki termal direnç;
𝑅𝑘𝑜𝑛𝑑 =
𝑇𝑠,1 −𝑇𝑠,2
𝑞𝑥
=
𝐿
(3-15)
𝑘𝐴
ve konveksiyondaki termal direnç;
𝑅𝑘𝑜𝑛𝑣 =
𝑇𝑠 −𝑇∞
𝑞𝑥
=
1
(3-16)
ℎ𝐴
qx miktarı sabit olduğu için,
𝑞𝑥 =
𝑇∞,1 −𝑇𝑠,1
1/ℎ1 𝐴
=
𝑇𝑠,1 −𝑇𝑠,2
𝐿/𝑘𝐴
=
𝑇𝑠,2 −𝑇∞,2
1/ℎ2 𝐴
(3-17)
Toplam sıcaklık farkı toplam dirence bölündüğünde de qx miktarı tespit edilebilir.
𝑇𝑜𝑝𝑙𝑎𝑚 𝑠𝚤𝑐𝑎𝑘𝑙𝚤𝑘 𝑓𝑎𝑟𝑘𝚤 = 𝑇∞,1 − 𝑇∞,2
1
𝑇𝑜𝑝𝑙𝑎𝑚 𝑡𝑒𝑟𝑚𝑎𝑙 𝑑𝑖𝑟𝑒𝑛ç; 𝑅𝑡𝑜𝑝𝑙𝑎𝑚 = ℎ
1𝐴
𝑞𝑥 =
𝐿
1
+ 𝑘𝐴 + ℎ
2𝐴
𝑇∞,1 −𝑇∞,2
𝑅𝑡𝑜𝑝𝑙𝑎𝑚
(3-18)
(3-19)
Şekil 3.10. Bir duvarda ısı transferi
42
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Konveksiyonla ısı transfer katsayısı küçük olduğu zaman, yüzeyle çevre arasında radyasyon
değişimi de önemlidir. Radyasyondaki termal direnç;
𝑅𝑟𝑎𝑑 =
𝑇𝑠 −𝑇ç𝑒𝑣𝑟𝑒
𝑞𝑟𝑎𝑑
=
1
ℎ𝑟 𝐴
(3-20)
Bir yüzeyle geniş bir çevre arasındaki radyasyonda, hr (radyasyon ısı transfer katsayısı)
değeri Denklem 3.12 den hesaplanabilir.
[ Hatırlatma: Denklem 3.12
2
ℎ = 𝜀𝜎(𝑇𝑠 + 𝑇ç𝑒𝑣𝑟𝑒 )(𝑇𝑠2 + 𝑇ç𝑒𝑣𝑟𝑒
)]
Temas Direnci
İki farklı malzeme temas haline getirildiğinde, arayüzeylerinde yani temas
yüzeylerinde bir termal temas direnci
oluşur. Bu temas noktasında bir
sıcaklık düşmesi meydana gelir, bu
nedenle ısı transferi hesaplamalarında
dikkate alınması gerekmektedir. Bu
temas direnci büyük ölçüde yüzey
pürüzlülüğüne bağlıdır. Yüzey pürüz
olduğunda, iki malzeme arasında
temas tam olarak gerçekleşmez ve
aralarında boşluklar oluşur. Bu hava
boşluğu oluşumu Şekil 3.11 de
gösterilmiştir.
Şekil 3.11. İki katı arasındaki temas direnci
Kompozit Duvarda Isı Transferi
Farklı termal iletkenlik katsayılarına sahip malzemelerden oluşturulmuş bir duvar örneğine
sıkça rastlarız. Farklı malzemelerin farklı termal dirençleri olması da söz konusudur. Böyle
bir duvar örneği Şekil 3.13 de verilmiştir. Bu duvar için tek boyutlu (x yönünde) ısı transferi
olduğunu göz önüne alalım. Burada ısı transferi;
𝑞𝑥 =
𝑇∞,1 −𝑇∞,3
∑𝑅
(3-21)
Bu durumda,
𝑞𝑥 =
𝑇∞,1 −𝑇∞,3
𝐿𝐴
𝐿𝐵
1
1
+
+
+
ℎ1 𝐴 𝑘 𝐴 𝐴 𝑘 𝐵 𝐴 ℎ3 𝐴
(3-22)
Bu denklem aynı zamanda aşağıdaki gibi de ifade edilebilir.
43
TAŞINIM OLAYLARI
𝑞𝑥 =
𝑇∞,1 −𝑇𝑠,1
1
ℎ1 𝐴
PROF.DR.KENAN YILDIZ
=
𝑇𝑠,1 −𝑇2
𝐿𝐴
𝑘𝐴 𝐴
=
𝑇2 −𝑇𝑠,3
𝐿𝐵
𝑘𝐵 𝐴
=
𝑇𝑠,3 −𝑇∞,3
1
ℎ3 𝐴
=⋯
(3-23)
Şekil 3.12. Kompozit duvarda ısı transferi
Kompozit sistemlerde “U” ile simgelenen, Toplam Isı Transfer Katsayısı vardır. ΔT terimine
toplam sıcaklık farkı dersek,
𝑞𝑥 = 𝑈𝐴 ∆𝑇
𝑈=
(3-24)
1
(3-25)
𝑅𝑇𝑜𝑝𝑙𝑎𝑚 𝐴
Bu durumda toplam direnci aşağıdaki gibi de ifade edebiliriz.
𝑅𝑇𝑜𝑝𝑙𝑎𝑚 = ∑ 𝑅 =
∆𝑇
𝑞
=
1
𝑈𝐴
(3-26)
Problem 3.16. Bir fırının kompozit duvarı üç farklı malzemeden (A, B ve C maddeleri)
yapılmıştır. Bu malzemelerden A’nın termal iletkenliği 20 W/m.K, C’nin termal iletkenliği 50
W/m.K dır. A malzemesinin kalınlığı 30 cm, B ve C malzemelerinin kalınlıkları ise 15 cm dir.
Fırındaki havanın sıcaklığı 800oC, konveksiyon sabiti (h) 25 W/m2K, fırın içindeki A
malzemesinin yüzey sıcaklığı 600oC dir. Dış yüzey sıcaklığı ise 20oC dir. B malzemesinin
termal iletkenlik katsayısını bulunuz.
44
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Çözüm.
𝑞𝑥 =
800−600
1
25.𝐴
= 5000
𝑊
𝑞𝑥 =
5000 =
(Birim alan için kabul edilmiştir)
𝑚2
600 − 20
0.3 0.15 0.15
20 + 𝑘𝐵 + 50
580
580
=
0.15
0.15
0.015 +
+ 0.003 0.018 +
𝑘𝐵
𝑘𝐵
5000 (0.018 +
90 +
0.15
) = 580
𝑘𝐵
750
= 580
𝑘𝐵
750
= 580 − 90 = 490
𝑘𝐵
750
𝑘𝐵 = 490 = 1.53
𝑊
𝑚.𝐾
Problem 3.17. Problem 3.14 de verilen verilere göre, A ile B arasındaki sıcaklık (T2) ve B ile
C malzemeleri arasındaki sıcaklık (T3) değerlerini bulunuz.
Çözüm. (A birim alanı için)
A-B malzemeleri arasındaki sıcaklık,
𝑞=
∆𝑇
𝐿𝐴
𝑘𝐴 𝐴
∆𝑇 = 600 − 𝑇2 = 5000 𝑥
0.3
= 75
20
𝑇2 = 600 − 75 = 525 oC
B-C malzemeleri arasındaki sıcaklık,
45
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑇3 = 𝑇2 − 5000 𝑥
0.15
1.53
= 525 − 490 = 35 oC
Problem (Vize, 2014): Bir evin duvarı 25 cm kalınlığında tuğla (kT=0,81 W/mK) ile örülmüş,
tuğlanın üzerine 5 cm kalınlığında strafor (yalıtım malzemesi) kaplanmıştır. Odanın sıcaklığı
22°C (h=7,7 W/m2K), dış ortam sıcaklığı ise -6°C dir (h=25 W/m2K). Tuğla ile yalıtım
malzemesi arasındaki sıcaklık 15°C olduğuna göre yalıtım malzemesi olan straforun termal
iletkenlik katsayısını bulunuz. (Radyasyon ihmal edilmiştir)
Çözüm.
Odanın hava sıcaklığı (22°C) ile Tuğla-yalıtım malzemesi arasındaki sıcaklık (15°C)
arasındaki bölge alındığında (birim alan için),
𝑞=
22−15
7
1 0,25
+
7,7 0,81
= 0,13+0,308 = 15,96 𝑊/𝑚2
Tüm sistem ele alındığında,
𝑞=
22−(−6)
1 0,25 0,05 1
+
+
+
7,7 0,81
𝑘
25
=
28
0,05
0,13+0,308+
+0,04
𝑘
28
0,478+
0,05
𝑘
= 15,96
0,798
𝑘
28 = 7,63 +
20,37 =
=
0,798
𝑘
𝑘 = 0,039 W/mK
Problem (Final, 2014): Bir bilgisayar odasının sıcaklığı 20°C de (h=30 W/m2K) sabit
tutulmak istenmektedir. Bu amaçla 3 tabakalı bir izolasyon düşünülmektedir. Oda tarafındaki
ilk malzeme 0,12 W/mK termal iletkenlik katsayısına sahip ve 10 mm kalınlığındadır.
Ortadaki malzemenin kalınlığı 10 cm’dir. En dıştaki malzeme ise 20 mm kalınlığında olup
0,25 W/mK termal iletkenlik katsayısına sahiptir. Dışarıdaki havanın sıcaklığı 39°C (h=60
W/m2K) olup bu üç tabakalı izolasyondan ısı kaybının maksimum 7 W/m 2 olması
istenmektedir. Bu durumda ortadaki yalıtım malzemesinin termal iletkenlik katsayısı ne
olmalıdır? (radyasyon ihmal edilmiştir)
Çözüm.
𝑞=
39−20
1 0,01 0,1 0,02 1
+
+ +
+
30 0,12 𝑘 0,25 60
7=
=7
19
0,213 +
1,491 +
0,1
𝑘
0,7
= 19
𝑘
𝑘 = 0,04
𝑊
𝑚𝐾
46
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem (Ödev 6, 2014): Bir fırın duvarı üç katmanlı olarak imal edilmiştir. Fırının içindeki
hava 870°C olup konveksiyon ısı iletim katsayısı 110 W/m2.K dir. Fırının iç kısmında 12 cm
kalınlığında ve 0.6 W/m.K termal iletkenlik katsayısına sahip bir refrakter tuğla, ortada 10 cm
kalınlığında ve 0.8 W/m.K termal iletkenlik katsayısına sahip bir ateş tuğlası, en dış kısma ise
termal iletkenliği 49 W/m.K olan 10 mm kalınlığında bir levha yerleştirilmiştir. Fırın
dışındaki hava 30°C olup konveksiyon ısı iletim katsayısı 15 W/m2.K dir. Fırının iç ve dış
yüzey sıcaklıkları ile katmanlar arasındaki sıcaklıkları bulunuz.
Çözüm.
𝑞=
870 − 30
840
840
=
=
1
0,12 0,1 0,01 1
0,0091 + 0,2 + 0,125 + 0,0002 + 0,0667 0,401
110 + 0,6 + 0,8 + 49 + 15
𝑊
= 2094,8 2
𝑚
870°C – T1 arasında konveksiyon var;
𝑞 = 2094,8 = 110 (870 − 𝑇1 )
2094,8
𝑇1 = 870 −
= 870 − 19 = 851 °𝐶
110
T1(851°C) – T2 arasında kondüksiyon var;
𝑞 = 2094,8 = 0,6
851 − 𝑇2
0,12
2094,8𝑥0,12
= 851 − 419 = 432°𝐶
0,6
T2(419°C) – T3 arasında kondüksiyon var;
𝑇2 = 851 −
𝑞 = 2094,8 = 0,8
432 − 𝑇3
0,1
2094,8𝑥0,1
= 432 − 262 = 170°𝐶
0,8
T3(170°C) – T4 arasında kondüksiyon var;
𝑇3 = 432 −
𝑞 = 2094,8 = 49
𝑇4 = 170 −
170 − 𝑇4
0,01
2094,8𝑥0,01
= 170 − 0,4 = 169,6°𝐶
49
47
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
BÖLÜM 4
KÜTLE TRANSFERİ
Kütle transferi, akışkanların hareketinden farklıdır. Bu olay, moleküllerin veya atomların bir
bünyeden diğerine, birbirleriyle temas ettikleri zaman taşınması şeklinde gerçekleşir. Örnek
olarak bir bakır levha bir çelik levha üzerine yerleştirildiğinde, bazı moleküller bir taraftan
diğer tarafa difüze olacaktır. Kısaca ifade etmek gerekirse, kütle transferi olabilmesi için
gerekli şart konsantrasyon gradyentidir (bileşim farklılığı).
Atomsal Hareketler
Malzemelerde üretim ve uygulama sırasında görülen katılaşma, çökelme, yeniden
kristalleşme, tane büyümesi gibi işlemler büyük ölçüde atomların kütle içinde hareketlerine
bağlıdır.
Termal enerji etkisinde oluşan
hareketler iki farklı aşamada oluşur.
Birincisi termal etki ile atomların
kendi denge konumları çevresindeki
küçük titreşim hareketleri, ikincisi
ise yine aynı etki ile bir denge
konumundan diğerine atlayarak
yaptıkları
uzak
mesafe
hareketleridir. Bu ikinci olaya
atomsal yayınım veya difüzyon
denmektedir. Atomsal
yayınım
sonucu cismin yapısı ve bu nedenle
de özellikleri değişmektedir.
Şekil 4.1. Farklı boyuttaki atomların yayınımı
Atomsal yayınım veya difüzyon denilen olayda sıcaklık arttıkça atomların termal titreşimleri
artar, çevresindekilerle bağları kopar, atomlararası boşluklardan geçerek yeni konumuna gelip
çevresiyle yeni bağ yaparlar.
Atomların kütle içindeki yayınımı üç şekilde gerçekleşir. Birincisi, boş kafes köşesi yayınımı
olup nispeten düşük bir enerji gerektirir. Bir kristal kafesinde varolan boş kafes köşesinin
çevresindeki komşu atomların bu boş köşeye atlama olasılıkları aynıdır. İkincisi, arayer
atomunun kafeste mevcut atomlar arasından geçerek oluşturduğu harekettir (Bakınız Şekil 4.1
– alt sağda - ). Buna arayer yayınımı denir ve oldukça yüksek enerji gerektirir. Halka yayınımı
denilen üçüncü yayınımın meydana gelme olasılığı düşük olmakla birlikte oldukça ilginçtir.
Birbirine değerek halka halinde bulunan atomlar aynı anda ve aynı yönde hareket ederek
birbirlerinin yerini alabilirler. Bu yayınım türü çok büyük enerji gerektirdiğinden ergime
sıcaklıklarına yakın bölgelerde gerçekleşebilirler.
Atomsal Yayınım Kuralları
Bir yayınım sistemi genellikle bir ana faz (çözen sistem) ile o fazın yapısında hareket eden
yabancı atomlardan (çözünen sistem) oluşmaktadır. Nikel kafesinde yayınan bakır atomları bu
duruma örnek verilebilir. Şekil 4.2 de üzeri bakırla kaplanmış bir nikel kristalini ele alalım.
48
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Başlangıçta kaplamada bulunan bütün atomlar bakırdır. Yüksek sıcaklıkta belirli bir zaman
dilimi sonrasında bakır ve nikelin birbiri içinde difüze olarak (yayınarak) ilerlediği
gözlenecektir.
Şekil 4.2. Bakır ve nikel atomlarının yayınması ve konsantrasyon profilleri
Şekil 4.3. Konsantrasyon profilindeki değişim
Şekil 4.3 de verilen A atomlarının x mesafesinde değişimi azalan bir eğri şeklinde olacaktır.
Konsantrasyonu “C” ile ifade edersek, konsantrasyon gradyantı,
−
𝑑𝐶
𝑑𝑥
olacaktır.
49
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Birinci Fick Kanunu
Şekil 4.3 de yüzeyden “x” kadar mesafede ve yüzeye paralel A (m2) alanından “t” (saniye)
zamanında “N” adet atomun geçtiğini varsayarsak, bu durumda Atomsal Yayınım Akısı (J);
𝐽=
𝑁
𝐴.𝑡
atom/m2.saniye
(4-1)
Birinci yayınım (difüzyon) kuralına göre atomsal yayınım akısı, o noktadaki konsantrasyon
gradyantı (dC/dx) ile doğru orantılıdır.
𝐽 = −𝐷
𝑑𝐶
(4-2)
𝑑𝑥
Burada D yayınım katsayısı olup birimi m2/sn dir. Yayınımın yönü dC/dx ‘in işaretinin tersi
yönünde olduğu için denkleme eksi işareti konmuştur. D yayınım katsayısı sıcaklığa, yayınım
sisteminin türüne ve yapısına bağlıdır. D’nin sıcaklığa bağlılığı Arhenius denklemiyle ifade
edilmektedir.
𝐷 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇
(4-3)
Burada D0 (m2/sn) yayınım sabiti, Q aktivasyon enerjisi, R gaz sabiti ve T mutlak sıcaklıktır.
Tablo 4.1 de bazı yayınım sistemlerinin yayınım sabitleri verilmiştir.
Tablo 4.1. Bazı yayınım sabitleri
Çözünen
C
C
Fe
Fe
Ni
Mn
Zn
Cu
Cu
Ag
Çözen
(ymk) Fe
(hmk) Fe
(ymk) Fe
(hmk) Fe
(ymk) Fe
(ymk) Fe
Cu
Al
Cu
Ag
D0 (m2/sn)
0,2.10-4
2,2.10-4
0,22.10-4
2.10-4
0,77.10-4
0,35.10-4
0,34.10-4
0,15.10-4
0,2.10-4
0,4.10-4
Q (kcal/mol)
34
29.3
64
57.5
67
67.5
45.6
30.2
47.1
44.1
Yayınım sabitlerinin yayınım sisteminin türü ve yapısına bağlılığı aşağıdaki şekilde
açıklanabilir;
1) Küçük atomlar daha kolay yayınır
2) Belirli bir atom ergime sıcaklığı düşük, dolayısıyla atomlararası bağı daha zayıf olan
ortamda daha kolay yayınır
3) Atomsal dolgu faktörü düşük ortamlarda yayınım daha az enerji gerektirir
4) Düzensiz yapıya sahip ve atom sıklığı tanelere göre daha az olan tane sınırları boyunca
yayınım daha kolay oluşur. Bu nedenle faz dönüşümleri ve korozyon olayları tane sınırlarında
başlar ve daha hızlı oluşur.
50
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem 4.1. Aluminyum, silisyum kristalinde yayındırılarak yarı iletken üretilecektir.
Sistemin aktivasyon enerjisi 73 kcal/mol ve yayınım sabiti 1,55.10-4 m2/sn dir. Hangi
sıcaklıkta yayınım katsayısı 10-14 m2/sn olur?
Çözüm:
𝐷 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇
ln(10−14 ) = ln(1,55. 10−4 ) −
−32,24 = −8,77 −
23,47 =
73000
1,987 . 𝑇
36738,8
𝑇
36738,8
𝑇
𝑇 = 1565 𝐾
Kütle Taşınımı Gerçekleşen Endüstriyel Örnekler
Sementasyon İşlemi
Az karbonlu çelik yumuşak ve sünektir, işlenmesi
kolaydır. Çeliğe şekil verdikten sonra sürtünmeye
maruz kalacak yüzeylere sementasyon işlemi
uygulayarak yüzeydeki karbon oranı arttırılır, sonra
su verme işlemi ile sertleştirilir. Sementasyon
işleminde az karbonlu çelik, aktif karbon atomları
içeren bir ortamda yüksek sıcaklıkta (800oC
üzerinde) bir süre ısıtılır. Karbon atomlarının
yayınması sonucu yüzeyde ince bir tabaka yüksek
karbonlu yapı oluşur. Bu şekilde semente edilmiş
çeliğe su verme işlemi uygulanırsa yüzeyi sert ve
aşınmaya dayanıklı, içi yumuşak ve tok bir malzeme
elde edilir. Örneğin motorların krank millerinin
(Şekil 4.4) sürtünen yüzeyleri sementasyon işlemi ile
sertleştirilir ve aşınmaya karşı dayanıklı hale
getirilir.
Şekil 4.4. Yüzeyi semente edilmiş
krank mili
Galvanizleme İşlemi
Demirin, özellikle de çelik sac ve boruların
korozyona karşı direncini arttırmak için ergimiş
çinko banyosuna daldırılır. Çinko, yüzeysel yayınma
sonucu demir yüzeyinde ince bir tabaka oluşturur.
Bu şekilde elde edilen galvanizli saclarda ve
borulardaki çinko tabakası ana metali korozyona
karşı korumaktadır.
Şekil 4.5. Boruların galvanizleme
işlemi
51
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Kaynak ve Lehim İşlemi
Metal parçalarını birleştirmek için uygulanan bu
işlemlerde yayınım olayından yararlanılır.
Kaynak işleminde iki metal parçası yüksek
sıcaklıkta ergitilerek aralarında uzak mesafeli
bir yayınım sağlanır. Ergitme kaynağı denen bu
işlemde ana metalle dolgu metali (elektrod) aynı
tür olursa eriyik daha kolay oluşur ve daha iyi
sonuç elde edilir. Ergitme için gaz alevi veya
elektrik arkı kullanılır. Diğer bir kaynak türünde
ergitme sıcaklığının altında çalışılır, ancak
parçaların temas yüzeylerinin oksit ve curuftan
arınmış olması gerekir. Bunun için uygun örtü
malzemesi (kaynak tozu) kullanılır.
Lehimde, dolgu metalinin ergime sıcaklığı,
birleştirilecek ana metalinkinin çok altındadır.
Dolgu metalinin ergime sıcaklığı 400oC nin
üzerinde ise sert lehim, altında ise yumuşak
lehim denir. Sert lehimde pirinç ve gümüş
alaşımları, yumuşak lehimde ise kurşun – kalay
alaşımları kullanılır. Lehim metalinin ergime
sıcaklığı yükseldikçe yayınım derinliği artar ve
daha mukavemetli bir birleşim sağlanır. Düşük
ergime sıcaklığı olan lehimlerde yayınım
düşüktür dolayısıyla mukavemet düşük olur. Bu
işlemlerde metallerin temas eden yüzeylerini
temizlemek ve oluşacak curufu uzaklaştırmak
için örtü malzemelerine (lehim pastası) ihtiyaç
vardır.
Şekil 4.6. Kaynak işlemi
Şekil 4.7. Lehimleme işlemi
Problem 4.2. Çinko atomları bakır içinde yayınmaktadır. Yüzeyden x1 derinliğinde 1 m3 de
1025 Zn atomu, x2 derinliğinde 1 m3 de 1023 Zn atomu vardır. x1 ile x2 arasındaki uzaklık 0,02
mm olup 500°C de x1 den x2 ye doğru oluşan yayınım akısını bulunuz. 500°C de çinkonun
bakır içindeki yayınım katsayısı 4.10-18 m2/sn dir.
Çözüm.
𝐽 = −𝐷
𝑑𝐶
𝐶2 − 𝐶1
= −𝐷
𝑑𝑥
𝑥2 − 𝑥1
𝑎𝑡𝑜𝑚
2 (1023 − 1025 )
𝑚
𝑚3
𝐽 = −4. 10−18
.
𝑠𝑛
0,02. 10−3 𝑚
𝐽 = 1,98. 1012
𝑎𝑡𝑜𝑚
𝑚2 . 𝑠𝑛
52
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem 4.3. 500°C de hmk-Fe içinde karbonun yayınma akısı 1012 C atomu/m2sn olduğuna
göre konsantrasyon gradyantını hesaplayınız. Karbonun 500°C da Fe içinde yayınma katsayısı
10-12 m2/sn dir.
Çözüm.
𝐽 = −𝐷
𝑑𝐶 𝑑𝐶
𝐽
1012 𝑎𝑡𝑜𝑚/𝑚2 𝑠𝑛
→
=− =−
= −1024 𝑎𝑡𝑜𝑚/𝑚4
𝑑𝑥
𝑑𝑥
𝐷
10−12 𝑚2 /𝑠𝑛
Problem 4.4. Demir içinde yayınan nikelin yayınım akısı 106 Ni atomu/cm2sn ise 1000°C de
ve 1400°C de nikelin konsantrasyon gradyantını bulunuz.
D1000=2.10-12 cm2/sn;
Q=67000 cal/mol;
D0=0,77.10-4 cm2/sn
Çözüm.
1000°C de konsantrasyon gradyantı;
𝑑𝐶
𝐽
106
=− =−
= −5. 1017 𝑎𝑡𝑜𝑚/𝑐𝑚4
𝑑𝑥
𝐷
2. 10−12
1400°C de konsantrasyon gradyantı;
𝐷1400 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇 = 0,77. 10−4 𝑒 −67000/1,987.1673 = 1,4. 10−9 𝑐𝑚2 /𝑠𝑛
𝑑𝐶
𝐽
106
=− =−
= −7. 1014 𝑎𝑡𝑜𝑚/𝑐𝑚4
−9
𝑑𝑥
𝐷
1,4. 10
Problem 4.5. Bir östenitik çelikte (YMK) nikelin 500oC de yayınım katsayısı 10-22 m2/sn,
1000oC de 10-15 m2/sn olduğuna göre nikelin yayınım aktivasyon enerjisini bulunuz.
Çözüm. T1=500oC=773 K
T2=1000oC=1273 K
T1 deki yayınım katsayısı: 𝐷1 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇1
T2 deki yayınım katsayısı: 𝐷2 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇2
T2 deki denklemi T1 deki denkleme böldüğümüzde,
𝑄 1 1
𝐷2
( − )
= 𝑒 𝑅 𝑇1 𝑇2
𝐷1
𝑙𝑛
𝑙𝑛
𝐷2 𝑄 1
1
= ( − )
𝐷1 𝑅 𝑇1 𝑇2
10−15
𝑄
1
1
=
(
−
)
−22
10
1,987 773 1273
16,118 = 𝑄 𝑥 2,557. 10−4
𝑄 = 63030 𝑐𝑎𝑙/𝑚𝑜𝑙
53
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem (Vize 2014-A): Gümüşün bakır içindeki yayınım (difüzyon) katsayıları sırasıyla
650°C de 5,5.10-16 m2/s ve 900°C de 1,3.10-13 m2/s dir. Gümüşün bakır içinde yayınma için
gerekli aktivasyon enerjisini, yayınma sabitini (D0) ve 800°C deki yayınma katsayısını
bulunuz. (R=1,987 cal/mol.K)
Çözüm.
ln
ln
𝐷1173 𝑄 1
1
= [ − ]
𝐷923
𝑅 𝑇1 𝑇2
1,3. 10−13
𝑄
1
1
=
[
−
]
−16
5,5. 10
1,987 923 1173
5,4654 = 𝑄 (1,162. 10−4 )
𝑄 = 47034,4 𝑐𝑎𝑙
D = D0 . e−Q/RT
5,5. 10−16 = 𝐷0 . 𝑒 −47034,4/1,987.923 = 𝐷0 (7,28. 10−12 )
𝐷0 = 7,55. 10−5 m2/s
800°C deki (1073 K) yayınma katsayısı,
𝐷 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇 = (7,55. 10−5 ). 𝑒 −47034,4/1,987.1073 = 1,98. 10−14
𝑚2
𝑠
Problem (Vize 2014-B): Çinkonun demir içindeki yayınım (difüzyon) katsayıları sırasıyla
627°C de 3,44.10-14 m2/s ve 827°C de 2,03.10-11 m2/s dir. Çinkonun demir içinde yayınma
için gerekli aktivasyon enerjisini, yayınma sabitini (D0) ve 750°C deki yayınma katsayısını
bulunuz. (R=1,987 cal/mol.K)
Çözüm.
ln
ln
𝐷1100 𝑄 1
1
= [ − ]
𝐷900
𝑅 𝑇1 𝑇2
2,03. 10−11
𝑄
1
1
=
[
−
]
−14
3,44. 10
1,987 900 1100
6,38 = 𝑄 (1,0167. 10−4 )
𝑄 = 62751,45 𝑐𝑎𝑙
D = D0 . e−Q/RT
3,44. 10−14 = 𝐷0 . 𝑒 −62751,45/1,987.900 = 𝐷0 (5,76. 10−16 )
54
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝐷0 = 59,7 m2/s
750°C deki (1023 K) yayınma katsayısı,
𝐷 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇 = (59,7). 𝑒 −62751,45/1,987.1023 = 2,34. 10−12
𝑚2
𝑠
Süreksiz Kütle Taşınımı
Genelde belirli bir zaman sürecinde gerçekleştirdiğimiz parçacıkların taşınımı (kütle transferi)
ile ilgileniriz. Örneğin bir çelik parçasının yüzeyi, yüksek sıcaklıkta bulunan bir fırında,
karbon içeren bir malzemeyle sertleştirilir. Fırındaki kısa süreli zaman periyodunda, karbon
molekülleri çelik yüzeyinin içerisine doğru difüze olur, yani yayınır, fakat çok az bir derinliğe
(birkaç milimetrelik) yayınırlar. Karbon konsantrasyonu yüzeyden içeriye doğru
eksponensiyel (üssel) olarak azalır. Sonuçta yüzeyi sert, iç kısımları daha yumuşak bir parça
elde edilir. Bu tür işlemlerde kullanılan denklem,
𝐶𝐴 (𝑥,𝑡)−𝐶𝐴 (𝑖)
𝐶𝐴 (𝑠)−𝐶𝐴 (𝑖)
= erf 𝜂 (
𝑥
2√𝐷𝑡
)
(4-4)
Burada, CA(i) başlangıçta A’nın konsantrasyonu, CA(s) yüzeyde A’nın konsantrasyonu,
CA(x,t) belirli bir süre sonunda belirli bir mesafedeki A’nın konsantrasyonu, D yayınım
katsayısı, x mesafe, t zamandır. Buradaki “erf” hata fonksiyonudur (error function). Tablo 4.2
de verilen tablo kullanılarak hata oranı düzeltilir.
Tablo 4.2. Hata fonksiyonları tablosu
Denklemde molar fraksiyon, kütle fraksiyonu ve yoğunluk da kullanılabilmektedir.
𝐶𝐴 (𝑥,𝑡)−𝐶𝐴 (𝑖)
𝐶𝐴 (𝑠)−𝐶𝐴 (𝑖)
=
𝑊𝐴 (𝑥,𝑡)−𝑊𝐴 (𝑖)
𝑊𝐴 (𝑠)−𝑊𝐴 (𝑖)
=
𝜌𝐴 (𝑥,𝑡)−𝜌𝐴 (𝑖)
𝜌𝐴 (𝑠)−𝜌𝐴 (𝑖)
= erf 𝜂 (
𝑥
2√𝐷𝑡
)
(4-5)
55
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem 4.6. Bir çeliğin yüzeyi karbon
içeren bir malzeme ile sertleştirilmektedir. Yandaki şekilden de görüldüğü
üzere çeliğin başlangıçtaki karbon
miktarı kütlece %0.15 dir. Karbonun
çelik içerisindeki yayınım katsayısı
4,8.10-10 m2/sn dir. Çeliğin yüzeyinde
karbonun denge konsantrasyonu kütlece
%1.2 olup yüzeyden 0.5 mm derinlikte
kütlece %1 karbon oluşması için fırında
tutulması gereken süreyi hesaplayınız.
Çözüm.
𝑊𝐴 (𝑥, 𝑡) − 𝑊𝐴 (𝑖)
𝑥
= erf 𝜂 (
)
𝑊𝐴 (𝑠) − 𝑊𝐴 (𝑖)
2√𝐷𝑡
0,01 − 0,0015
𝑥
= erf 𝜂 (
)
0,012 − 0,0015
2√𝐷𝑡
0,81 = erf 𝜂 (
𝑥
2√𝐷𝑡
)
Hata fonksiyonunda 0,81’in karşılığı yaklaşık olarak 0,17 dir. (Tablo 4.2 den alınmıştır)
𝑥
2√𝐷𝑡
𝑥2
𝑡=
=
4𝐷(0,17)2
= 0,17
(0,0005 𝑚)2
= 4505 𝑠𝑛 = 1 𝑠𝑎𝑎𝑡 15 𝑑𝑎𝑘
𝑚2
4 (4,8. 10−10 𝑠𝑛 ) (0,17)2
Problem 4.7. Karbon miktarı %0.12 olan bir çelik parça, karbürleyici gazla temas ettirilerek
1150 K deki bir fırında yüzeyi sertleştirilmektedir. Karbonun çelikteki difüzyon katsayısı
sıcaklığa kuvvetli şekilde bağlı olup mevcut fırın sıcaklığında 7,2.10-12 m2/sn dir. Yüzeydeki
karbonun kütle fraksiyonu ise 0,011 dir. 0,7 mm derinlikte %0,32 karbon bulunması için bu
çelik parça fırında ne kadar süre tutulmalıdır.
Çözüm.
𝑊𝐴 (𝑥, 𝑡) − 𝑊𝐴 (𝑖)
𝑥
= erf 𝜂 (
)
𝑊𝐴 (𝑠) − 𝑊𝐴 (𝑖)
2√𝐷𝑡
0,0032 − 0,0012
𝑥
= erf 𝜂 (
)
0,011 − 0,0012
2√𝐷𝑡
0,204 = erf 𝜂 (
𝑥
2√𝐷𝑡
)
56
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Hata fonksiyonunda 0,204’in karşılığı yaklaşık olarak 0,9 dur. (Tablo 4.2 den alınmıştır)
𝑥
2√𝐷𝑡
𝑥2
𝑡=
=
4𝐷(0,9)2
= 0,9
(0,0007 𝑚)2
= 21005 𝑠𝑛 = 350 𝑑𝑎𝑘
𝑚2
4 (7,2. 10−12 𝑠𝑛 ) (0,9)2
Problem 4.8. Problem 4.7 deki işlem 500 K de gerçekleştirilseydi ne kadar sürede olay
tamamlanırdı. Bu sıcaklıkta D=2,1.10-20 m2/sn
Çözüm. Başlangıç hesaplamaları aynıdır.
𝑥
2√𝐷𝑡
𝑥2
𝑡=
=
4𝐷(0,9)2
= 0,9
(0,0007 𝑚)2
= 7,2. 1012 𝑠𝑛 = 2. 109 𝑠𝑎𝑎𝑡
𝑚2
−20
2
(0,9)
4 (2,1. 10
𝑠𝑛 )
Görülmektedir ki bu sıcaklıkta yüzey sertleştirme işleminin yapılması uygun değildir.
Problem 4.9. Çinkonun demir içinde yayınma sabiti (D0) 60 cm2/sn, yayınma aktivasyon
enerjisi ise 262,6 kJ/mol dür. 900 K ve 1100 K de demir içerisinde aynı mesafede çinko
yayınması sağlayabilmek için düşük sıcaklıktaki deney süresi, yüksek sıcaklıktaki deney
süresinden kaç kat daha uzundur?
Çözüm.
900 K için D değeri (yayınma katsayısı);
𝐷900 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇 = (60). 𝑒 −262600/8,314𝑥900 = 3,44. 10−14
1100 K için D değeri (yayınma katsayısı);
𝐷1100 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇 = (60). 𝑒 −262600/8,314𝑥1100 = 2,03. 10−11
𝑥
2√𝐷900 . 𝑡900
=
𝑥
2√𝐷1100 . 𝑡1100
𝐷900 . 𝑡900 = 𝐷1100 . 𝑡1100
𝑡900
𝐷1100 2,03. 10−11
=
=
= 590 𝑘𝑎𝑡
𝑡1100
𝐷900
3,44. 10−14
57
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Problem 4.10. Aşağıdaki şekilde düşük karbonlu (%0,15 C) bir çeliğin 900°C de 2 saatlik
sürede karbürleyici bir ortamda yapılan sementasyon işlemleri sonucunda, çeliğin yüzeyden
içeriye doğru farklı derinliklerdeki (mesafelerdeki) karbon % değerleri grafiği verilmiştir. 0,2
mm derinlikteki karbon değerlerini göz önüne alarak difüzyon hızını (difüzyon katsayılarını)
bulunuz.
Çözüm.
2 saatlik (7200 sn) çalışma için, C(i)=0,0015; C(s)=0,0076; C(x,t)=0,0053; x=0,0002 m
𝐶(𝑥, 𝑡) − 𝐶(𝑖)
𝑥
= erf 𝜂 (
)
𝐶(𝑠) − 𝐶(𝑖)
2√𝐷𝑡
0,0053 − 0,0015
0,0002
= erf 𝜂 (
) = 0,62
0,0076 − 0,0015
2√𝐷. 7200
Tablo 4.2 den,
0,0002
2√𝐷. 7200
= 0,35
𝐷 = 1,13. 10−11 m2/sn
Problem (Final, 2014): %0,2 C içeren bir YMK Fe-C alaşımı, belirli bir scaklıkta yüzeyde
%1 C oluşacak şekilde karbürizasyon işlemine tabi tutulmaktadır. 49,5 saat sonunda 4 mm
derinlikte %0,35 C olduğu tespit edilmiştir. Karbonun YMK demir içinde yayınma sabiti
2,3.10-5 m2/sn, bu yayınma için gerekli enerjinin 148 kJ/mol olduğu bilindiğine göre,
karbürizasyon işleminin yapıldığı sıcaklığı bulunuz. (R=8,314 j/mol.K)
Çözüm.
𝐶𝑥 − 𝐶0
𝑥
= 𝑒𝑟𝑓 (
)
𝐶𝑠 − 𝐶0
2√𝐷. 𝑡
58
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
0,35 − 0,2
= 𝑒𝑟𝑓(𝑧)
1 − 0,2
𝑒𝑟𝑓(𝑧) = 0,1875
Tablodan yaklaşık z=0,93
𝑥
2√𝐷. 𝑡
𝐷=
= 0,93
(0,004)2
𝑥2
=
(0,93)2 4𝑡 3,4596𝑥(49,5𝑥60𝑥60)
𝐷 = 2,6. 10−11 𝑚2 /𝑠𝑛
Karbürizasyon sıcaklığı,
𝐷 = 𝐷0 . 𝑒 −𝑄/𝑅𝑇
ln 𝐷 = ln 𝐷0 −
𝑇=
𝑄
𝑅𝑇
−𝑄
−148000
=
𝑅(ln 𝐷 − ln 𝐷0 ) 8,314𝑥(ln 2,6. 10−11 − ln 2,3. 10−5 )
=
𝑇=
−148000
8,314𝑥[(−24,373) − (−10,68)]
−148000
−148000
=
= 1300 𝐾
8,314𝑥(−13,693) −113,843
59
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
BÖLÜM 5
HETEROJEN REAKSİYONLARIN KİNETİĞİ
Homojen ve Heterojen Reaksiyonlar
Aynı fazda oluşan reaksiyonlar homojen reaksiyonlar olarak gerçekleşirken, birden fazla faz
arasında oluşan reaksiyonlar heterojen reaksiyon süreçleridir.
Reaksiyonların bir kısmı, azot monoksidin veya karbon monoksidin yanmasındaki gibi,
reaktanların (reaksiyona girenlerin) veya ürünlerin tümünün aynı fazda (özellikle gaz fazında)
bulunduğu kimyasal değişmelerdir. Aşağıda bir homojen reaksiyon örneği verilmiştir.
CO(g) + ½ O2(g) = CO2(g)
Bazı reaksiyonlarda ise, katı kömürün oksijen gazı ile yanma reaksiyonundaki gibi, maddenin
farklı fazlarındaki reaktanlar yer alır. Bu tür reaksiyonlara da heterojen reaksiyonlar denir.
Heterojen reaksiyonlar, reaktanlar arasındaki arayüzeylerle karakterize edilirler. Örneğin bir
katı–gaz reaksiyonunda arayüzey gazla temas halindeki katının dış yüzeyidir. Sıvı–sıvı
reaksiyonunda ise arayüzey, yan yana iki sıvı arasındaki temas yüzeyidir.
Bütün heterojen reaksiyonları arayüzey tabiatına bağlı olarak 5 kategoriye ayırmak
mümkündür. Bunlar; katı–gaz, katı–sıvı, katı–katı, sıvı–sıvı ve sıvı–gaz reaksiyonlarıdır.
Heterojen reaksiyonlardaki kimyasal değişmeler iki farklı faz arasındaki arayüzeyde
gerçekleşir. Heterojen reaksiyonlarda katı haldeki bir reaktantın yüzey alanı ne kadar büyük
olursa, reaksiyon da o ölçüde hızlı gerçekleşir. Talaş haline getirilmiş bir odunun kütük
halindeki oduna kıyasla çok daha hızlı yanması yüzey alanından kaynaklanmaktadır. Yüzey
alanının büyütülmesi ile reaktan tanecikleri arasındaki çarpışma sayısı artmakta, bu da
reaksiyonun hızlanmasını sağlamaktadır.
Arayüzeyin Tabiatı ( Doğası )
Katıları içeren reaksiyonlarda (katı–gaz, katı–sıvı, katı–katı) arayüzeyin tabiatı, bu
proseslerin kinetik incelemesinde rol oynar. Katı içindeki atom ve iyon hareketlerinin çoğu
kristal hataları veya boşlukları ile olur. Kimyasal reaksiyonlar bu latis hataları ve boşlukların
olduğu yerlerde çekirdeklenerek reaksiyon başlar.
Katıların kafes yapıları da reaksiyonun hızı üzerinde etkilidir. ADK (APF) düşük olanın
reaksiyon hızı, ADK daha büyük olanınkinden daha yüksektir.
60
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Tablo 5.1. Arayüzeylerine göre heterojen reaksiyon türleri
ARAYÜZEY
TİP
ÖRNEK
Katı – Gaz
K1 + G → K2
Fiziksel: Adsorbsiyon (yüzeye tutunma)
K1 → K2 + G
Kimyasal: Karbonatların parçalanması
K1 + G1 → K2 + G2
CaCO3(k) → CaO(k) + CO2(g)
Redüklenme reaksiyonu
Fe2O3(k) + 3CO(g) → 2Fe(k) + 3CO2(g)
Katı – Sıvı
K→S
Fiziksel: Ergime
K + S1 → S 2
Kimyasal: Çözünme, Liç işlemi,
K + S1 → K + S 2
Sementasyon
K1 + S1 → K2 + S2
Katı – Katı
K1 → K2
Fiziksel: Sinterleme, Faz dönüşümü
K1 + K2 → K3 + K4
Kimyasal: Oksitlerin C ile redüklenmesi,
K1 + K2 → K3 + G
FeO(k) + C(k) → Fe(k) + CO(g)
Oksitlerin metallerle redüklenmesi
Cr2O3(k) + 2Al(k) → 2Cr(k) + Al2O3(k)
Sıvı – Gaz
S→G
Fiziksel: Damıtma, Yoğunlaştırma
S1 + G → S2
Kimyasal: Çelik üretiminde oksijen üfleme
S1 + G1 → S2 + G2
işlemi, suda gazların absorblanması
Sıvı – Sıvı
S1 → S2
Curuf – metal reaksiyonları
Şekil 5.1. Kafes kusurları
61
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Arayüzeyin Alanı
Heterojen
reaksiyonlarda
reaksiyona
giren
maddelerin bir fazdan diğerine taşınmaları gerekir.
Buradaki transfer hızı (taşınan maddenin miktarı),
arayüzey alanına bağlıdır. Katı madde ile gerçekleşen
reaksiyonlarda küçük partiküller büyük yüzey alanı
oluşturduğundan, büyük partiküllere nazaran daha
hızlı reaksiyona girerler.
Yüzey alanının reaksiyon hızına etkisine örnek, FeS2’nin sulu ortamdaki oksidasyon hızına,
yüzey alanının etkisi verilebilir. Şekilden gözlendiği gibi FeS2’nin yüzey alanı arttıkça
reaksiyon hızı da artmaktadır. Sıvı–sıvı reaksiyonlarında ise karıştırma işlemi ile geniş yüzey
alanına sahip sıvı damlacıkları oluşturulur ve reaksiyon hızı arttırılır.
Şekil 5.2. FeS2’nin sulu ortamdaki oksidasyon hızına, yüzey alanının etkisi
Arayüzeyin Geometrisi
Heterojen reaksiyonlarda sıvı ya da gazla reaksiyona giren katının şekli, proseslerin
belirlenmesinde önemli rol oynar. Katı madde disk veya plaka şeklinde ise reaksiyon
arayüzeyi reaksiyon boyunca sabit kalır.
62
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Şekil 5.3. Küresel katı partikülün çözünme reaksiyonundaki davranışı
Küre veya küp gibi katı maddelerde ise reaksiyon arayüzeyi, reaksiyon boyunca değişir yani
azalır. Örnek olarak bir metalin asit içerisinde çözünmesini (katı-sıvı reaksiyon) ele alalım.
Burada hız;
𝑑𝑊
𝐻𝚤𝑧 = −
= 𝑘. 𝐴. 𝐶
𝑑𝑡
Burada W: katının ağırlığı, A: yüzey alanı, C: akışkan konsantrasyonu, t: zaman, k: reaksiyon
hız sabitidir. (-) işaretinin anlamı zamanla kütlenin azalması gösterir. Genel olarak süreçte
akışkan konsantrasyonunun değişmediği kabul edilir.
HIZ EŞİTLİĞİNİN REAKSİYON ORANI TERİMİYLE İFADESİ
Bir katı maddenin kimyasal reaksiyonunda, değişim veya dönüşüm reaksiyonlarında sürecin
gerçekleşme oranı (R) belirlenebiliyorsa kinetik çözümü de mümkündür. Bir katı madde, bir
asit içerisinde çözünürse;
𝑅 (𝑅𝑒𝑎𝑘𝑠𝑖𝑦𝑜𝑛 𝑔𝑒𝑟ç𝑒𝑘𝑙𝑒ş𝑚𝑒 𝑜𝑟𝑎𝑛𝚤) =
𝐴ğ𝚤𝑟𝑙𝚤𝑘𝑡𝑎𝑘𝑖 𝑑𝑒ğ𝑖ş𝑖𝑚 𝑊0 − 𝑊 ∆𝑊
=
=
𝑊0
𝑊0
İ𝑙𝑘 𝑎ğ𝚤𝑟𝑙𝚤𝑘
Katı maddenin geometrik şekline bağlı olarak formulasyon değişim gösterir. Reaksiyon
süreçlerinin gerçekleşme oranlarını belirlemek için ağırlık değişimleri izlendiği gibi;
geometriden de yararlanılabilir. Bu durumda kütlenin ne kadarında reaksiyonun gerçekleştiği
belirlenmelidir.
Küresel katı partikül için,
4 3
4 3
𝑊0 − 𝑊 3 𝜋𝑟0 . 𝑑 − 3 𝜋𝑟 . 𝑑 𝑟03 − 𝑟 3
𝑟3
𝑅=
=
=
=1− 3
4 3
𝑊0
𝑟03
𝑟0
𝜋𝑟
.
𝑑
3 0
𝑟 3
( ) =1−𝑅
𝑟0
63
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑟
= (1 − 𝑅)1/3
𝑟0
𝑟 = 𝑟0 (1 − 𝑅)1/3 (1 nolu denklem)
𝐴 = 4𝜋𝑟 2
𝐻𝚤𝑧 = −
𝑑𝑊
= 𝑘. 𝐴. 𝐶
𝑑𝑡
4
𝑊 = 𝜋𝑟 3 . 𝑑
3
4
𝑑𝑊 = 3. 𝜋𝑟 2 . 𝑑. 𝑑𝑟 = 4𝜋𝑟 2 . 𝑑. 𝑑𝑟
3
−4𝜋𝑟 2 . 𝑑.
𝑑𝑟
= 𝑘. 4𝜋𝑟 2 . 𝐶
𝑑𝑡
𝑟
𝑡
𝑘. 𝐶
− ∫ 𝑑𝑟 =
∫ 𝑑𝑡
𝑑
𝑟0
𝑟0 − 𝑟 =
0
𝑘. 𝐶. 𝑡
𝑑
Yukarıdaki bir nolu denklemi kullanabiliriz (r yerine r0’lı ifade ile)
𝑟0 − 𝑟0 (1 − 𝑅)1/3 =
𝑘. 𝐶. 𝑡
𝑑
Bu durumda genel denklem;
𝟏 − (𝟏 − 𝑹)𝟏/𝟑 =
𝒌. 𝑪
𝒕
𝒓𝟎 . 𝒅
Problem 5.1.Yoğunluğu 4.5 g/cm3 olan 15 mm çapındaki 7.95 g Fe2O3 peleti H gazı ile 900°C
de redüklenmektedir. Redüksiyonun ilk 30 dk. da peletin ağırlığı 1.12 gr azalmıştır. Reaksiyon
hız sabiti k’ yı bulunuz. (Fe:56, O:16)
Fe2O3 + 3H2 → 2Fe + 3H2O
Çözüm.
Fe2O3 peletindeki gerçekleşecek ağırlık azalması, katı kütleden oksijenin gitmesiyle
gerçekleşecektir. Bu durumda ilk ağırlık peletin ağırlığı değil, peletteki oksijen miktarıdır.
𝑊0 = ∑ 𝑂2 = 7,95 𝑥
3 𝑥 16
48
= 7,95 𝑥
= 2,385 𝑔
(2𝑥56) + (3𝑥16)
160
64
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
𝑅=
∆𝑊
1,12
=
= 0,4696
𝑊0 2,385
R değeri 0 ile 1 arasında çıkması gereken bir değerdir. Yukarıda bulduğumuz R değeri 0,4696
çıkmıştır. Bunun anlamı reaksiyon %46,96 gerçekleşmiştir.
1 − (1 − 𝑅)1/3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
C değeri her zaman “1” alınır. Çap 15 mm olduğuna göre yarıçap, cm cinsinden 0,75 cm’dir.
(yoğunlukta cm3 olduğu için yarıçap ta cm cinsinden olmalıdır)
1
1 − (1 − 0,4696)3 =
𝑘
𝑥 30
0,75 𝑥 4,5
0,1905 = 𝑘 𝑥 8,8889
𝑘 = 0,0214
𝑔
𝑐𝑚2 . 𝑑𝑘
Problem 5.2. Küre biçiminde 16 mm çapındaki ve 4.28 g/cm3 yoğunluğundaki 9.18 g FeO
farklı sıcaklıklarda saf CO gazı ile FeO + CO → Fe + CO2 reaksiyonu gereğince
redüklenmektedir. 20 dk süre sonunda Üç sıcaklık için saptanan ağırlık azalması; 980°C de
0.632 g, 1040°C de 0.775 g, 1100°C de 0.959 g olmuştur.
a) Her üç sıcaklık için reaksiyon hız sabitlerini
b) Reaksiyonun aktivasyon enerjisini hesaplayınız.
Çözüm.
Bu soruda dikkat edilirse FeO deki ağırlık azalması, yapıdan oksijenin gitmesi ile olmaktadır.
Bu durumda 9,18 g FeO içindeki oksijen miktarı W0 (ilk ağırlık) değeri olacaktır.
𝑊0 = ∑ 𝑂2 = 9,18 𝑥
16
16
= 9,18 𝑥
= 2,04 𝑔
56 + 16
72
980°C için,
𝑅=
∆𝑊 0,632
=
= 0,3098
𝑊0
2,04
1 − (1 − 𝑅)1/3 =
1
1 − (1 − 0,3098)3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
𝑘
𝑥 20
0,8 𝑥 4,28
0,11626 = 𝑘 𝑥 5,8411
𝑘 = 0,0199
𝑔
𝑐𝑚2 . 𝑑𝑘
65
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
1040°C için,
𝑅=
∆𝑊 0,775
=
= 0,3799
𝑊0
2,04
1 − (1 − 𝑅)1/3 =
1
1 − (1 − 0,3799)3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
𝑘
𝑥 20
0,8 𝑥 4,28
0,14725 = 𝑘 𝑥 5,8411
𝑔
𝑘 = 0,0252
𝑐𝑚2 . 𝑑𝑘
1100°C için,
𝑅=
∆𝑊 0,959
=
= 0,47
𝑊0
2,04
1 − (1 − 𝑅)1/3 =
1
1 − (1 − 0,47)3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
𝑘
𝑥 20
0,8 𝑥 4,28
0,19073 = 𝑘 𝑥 5,8411
𝑘 = 0,03265
𝑔
𝑐𝑚2 . 𝑑𝑘
Reaksiyonun aktivasyon enerjisi, herhangi iki sıcaklığı ve bu sıcaklıklardaki reaksiyon hız
sabitleri alınarak hesaplanabilir.
ln
ln
𝑘1 𝐸 1
1
= [ − ]
𝑘2 𝑅 𝑇2 𝑇1
0,0252
𝐸
1
1
=
[
−
]
0,03265 1,987 1373 1313
−0,259 = 𝐸 (−1,675. 10−5 )
𝐸 = 15462,6 𝑐𝑎𝑙/𝑚𝑜𝑙
Problem 5.3. 20 mm çaplarındaki ve 7.64 gr/cm3 yoğunluğunda 32 g Fe bilyalar ayrı ayrı
geniş kaplar içerisinde çözünmektedir. 3 farklı sıcaklıkta yapılan bu çözündürme işlemlerinin
40. dakikalarında bilyaların ağırlıklarının 80°C de 22.56 g, 120°C de 20 g ve 170°C de 16.93
g olduğu belirlenmiştir. Her 3 sıcaklık için çözünme hızı sabitlerini ve aktivasyon enerjisini
hesaplayınız ?
66
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Çözüm.
80°C için,
𝑅=
∆𝑊 32 − 22,56
=
= 0,295
𝑊0
32
1 − (1 − 𝑅)1/3 =
1
1 − (1 − 0,295)3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
𝑘
𝑥 40
1 𝑥 7,64
0,10998 = 𝑘 𝑥 5,2356
𝑘 = 0,021
𝑔
𝑐𝑚2 . 𝑑𝑘
120°C için,
𝑅=
∆𝑊 32 − 20
=
= 0,375
𝑊0
32
1 − (1 − 𝑅)1/3 =
1
1 − (1 − 0,375)3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
𝑘
𝑥 40
1 𝑥 7,64
0,145 = 𝑘 𝑥 5,2356
𝑘 = 0,0277
𝑔
𝑐𝑚2 . 𝑑𝑘
170°C için,
𝑅=
∆𝑊 32 − 16,93
=
= 0,4709
𝑊0
32
1 − (1 − 𝑅)1/3 =
1
1 − (1 − 0,4709)3 =
𝑘. 𝐶
.𝑡
𝑟0 . 𝑑
𝑘
𝑥 40
1 𝑥 7,64
0,1912 = 𝑘 𝑥 5,2356
𝑘 = 0,0365
𝑔
𝑐𝑚2 . 𝑑𝑘
Reaksiyonun aktivasyon enerjisi, herhangi iki sıcaklığı ve bu sıcaklıklardaki reaksiyon hız
sabitleri alınarak hesaplanabilir.
67
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
ln
ln
𝑘1 𝐸 1
1
= [ − ]
𝑘2 𝑅 𝑇2 𝑇1
0,021
𝐸
1
1
=
[
−
]
0,0277 1,987 393 353
−0,27691 = 𝐸 (−1,451. 10−4 )
𝐸 = 1908,3 𝑐𝑎𝑙/𝑚𝑜𝑙
Problem (Final, 2014): 80 g katı AB2 maddesi AB2(k) → A(k) + B2(g) reaksiyonuna göre
800°C de parçalanmaktadır. Numune ağırlığının 30 dakika sonunda 65 g olduğu tespit
edildiğine göre reaksiyon gerçekleşme oranı ne olur? (A:60 g/mol, B:20 g/mol)
Çözüm.
AB2: 100 g/mol, Bu durumda gidecek madde B maddesi (Numunenin %40’ı)
W0= 80 x 0,4 = 32 g
𝑅=
∆𝑊 80 − 65
=
= 0,469
𝑊0
32
Problem (Bütünleme, 2014): 100 g katı Al(OH)3 maddesi 800°C de kalsine edilmekte ve
aşağıdaki reaksiyona göre alumina (Al2O3) elde edilmektedir. 30 dakika sonunda numune
ağırlığı 80 g geldiğine göre bu süre sonunda reaksiyonun gerçekleşme oranını bulunuz.
(Al:27, O:16, H:1)
2Al(OH)3(k) → Al2O3(k) + 3H2O(g)
Çözüm.
2Al(OH)3(k) → Al2O3(k) + 3H2O(g)
(156 g)
(54 g)
W0 = 100 x
𝑅=
54
= 34,6 g
156
∆𝑊 100 − 80
=
= 0,578
𝑊0
34,6
Problem (Kısa Sınav 2, 2014): Krom oksit cevheri aşağıdaki reaksiyona göre CO ile
redüklenmektedir. Bu amaçla 5,2 g/cm3 yoğunluğundaki ve 10 mm çapında küresel katı
partiküllerden oluşan 100 g cevher, farklı sıcaklık ve sürelerde inert bir atmosferde fırında
tutulmuştur. Fırın çalışması sonunda numuneler tekrar tartılmış olup sonuçlar aşağıdaki
tabloda verilmiştir. Buna göre;
68
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
a) Her iki sıcaklık için reaksiyon hız sabitlerini
b) Reaksiyonun aktivasyon enerjisini hesaplayınız.
Redüklenme reaksiyonu: Cr2O3 + 3CO = 2Cr + 3CO2
(Cr:52; O:16; C:12)
Redüksiyon süresi
60 dakika
Numune ağırlığı
Çözüm.
Redüksiyon Sıcaklığı
1200°C
1400°C
95,6 g
73,2 g
W0 = 100x
1200°C için,
48
= 31,58 g
152
∆𝑊 100 − 95,6
=
= 0,139
𝑊0
31,58
1
𝑘. 𝐶
1 − (1 − 𝑅)3 =
.𝑡
𝑟0 . 𝑑
1
𝑘
1 − (1 − 0,139)3 =
𝑥60
0,5𝑥5,2
𝑔
𝑘 = 0,0021
2
𝑐𝑚 . 𝑑𝑘
𝑅=
1400°C için,
∆𝑊 100 − 73,2
=
= 0,848
𝑊0
31,58
1
𝑘. 𝐶
1 − (1 − 𝑅)3 =
.𝑡
𝑟0 . 𝑑
1
𝑘
1 − (1 − 0,848)3 =
𝑥60
0,5𝑥5,2
𝑔
𝑘 = 0,02
2
𝑐𝑚 . 𝑑𝑘
Reaksiyonun aktivasyon enerjisi,
𝑘1 𝐸 1
1
ln = [ − ]
𝑘2 𝑅 𝑇2 𝑇1
𝑅=
ln
0,0021
𝐸
1
1
=
[
−
]
0,02
1,987 1673 1473
(−2,254) = (−4,085. 10−5 )𝑥𝐸
𝐸 = 55177 𝑐𝑎𝑙
69
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Heterojen Reaksiyonların Mekanizması
Heterojen reaksiyonlar 5 temel kademeden gerçekleşir.
Bunlar;
1) Akışkandaki etkin maddenin katıya doğru yayınması
(difüzyon)
2) Etkin maddenin katı yüzeyine tutunması
(adsorbsiyon)
3) Arayüzeyde kimyasal reaksiyon
4) Oluşan ürünün veya ürün dışı maddenin arayüzeyden
ayrılması (desorbsiyon)
5) Ürünün akışkan içinde yayınması (difüzyon)
Nernst sınır tabakasının (δ) ve ilave olarak reaksiyon ürünlerinin oluşturduğu tabakaların
varlığının sonucu olarak, heterojen reaksiyonlar en yavaş adıma bağlı olarak;
a) Yayınım (difüzyon) kontrollü
b) Kimyasal reaksiyon kontrollü
c) Karışım kontrollü
Arayüzeydeki kimyasal reaksiyon hızı arayüzeydeki reaktanların difüzyon hızından daha hızlı
olabilir. Bu nedenle bu tip reaksiyonlar difüzyon kontrollü reaksiyonlar olarak adlandırılır.
Buna karşılık kimyasal reaksiyonun hızı arayüzeye reaktanların difüzyon hızından daha yavaş
olabilir. Bu durumda proses kimyasal reaksiyon kontrollü olarak ifade edilir.
Bir reaksiyonun kimyasal reaksiyon kontrollü veya difüzyon (yayınma) kontrollü olarak
devam etmesine,
1) Akışkan maddenin hızı
2) Sıcaklık
3) Etkili madde konsantrasyonu
etki etmektedir.
Akışkan Maddenin Hızının Etkisi: Katı madde–akışkan madde reaksiyonlarında karıştırma
hızındaki artış, çözünme hızında da artış sağlar. Bu durum difüzyon kontrollü reaksiyonlarda
gözlenir.
𝐻𝐼𝑍 =
𝐷
𝐴. 𝐶
𝛿
D, difüzyon (yayınma) hızı, δ ise Nerst sınır tabakasının kalınlığıdır. Sınır tabakasının
kalınlığı artan karıştırma hızı ile azalır. Dolayısıyla çözünme hızı artar. Çözünme hızı,
karıştırma hızının artması ile doğrusal olarak artmaz (Genellikle, sıvı arayüzeyinde hava
boşluklarının oluşması gibi diğer faktörlerden etkilenir). Kimyasal kontrollü reaksiyon
70
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
süreçleri karıştırma hızından bağımsızdır, karıştırma hızının reaksiyon hızı üzerine etkisi
yoktur.
Katı madde – gaz (akışkan) madde reaksiyon süreçlerinde, yayınma kontrollü süreçlerde,
reaksiyonlar gazın akış hızına bağlı iken; kimyasal kontrollü süreçlerde bağlı değildir. Düşük
gaz akış hızlarında, reaksiyon süreci genellikle yayınma kontrollüdür. Yani reaksiyon süreci,
katıyı saran sınır tabakası içinden gaz moleküllerinin yayınma hızına bağlıdır.
Sıcaklığın Etkisi: Yayınma kontrollü reaksiyonlar sıcaklığa zayıf şekilde bağlı iken, kimyasal
kontrollü reaksiyonlar sıcaklığa kuvvetle bağlıdır. Nedeni yayınma katsayısı sıcaklığa lineer
olarak bağlı iken; kimyasal reaksiyon hız sabiti exponansiyel (üssel) olarak bağlıdır.
Katı-katı dışındaki reaksiyon süreçlerinde ortam sıcaklığı 2 katına çıkartılırsa, difüzyon hızı 2
kat artarken, kimyasal reaksiyon hızı 100 kat artar.
Düşük sıcaklıkta kimyasal kontrollü prosesler, yüksek sıcaklıkta yayınma kontrollüye
dönüşebilir. Bunun nedeni; düşük sıcaklıkta çok düşük olan kimyasal reaksiyon hızının
(proses kimyasal kontrollü) yükselen (artan) sıcaklıkla yayınma hızından daha büyük
değerlere gelmesidir (Hız yayınma kontrollü hale gelir)
Katı-gaz reaksiyonlarında, artan sıcaklık ile kimyasal kontrollü mekanizmadan yayınma
(difüzyon) kontrollü mekanizmaya dönüşebilir.
Reaksiyon ürünü olarak oluşan madde, dış kabukta porozitesiz (boşluksuz) film (ürün)
oluşturarak reaksiyonun arayüzeye yayınması yavaşlayacağından yüksek sıcaklıkta yayınma
kontrollü mekanizma hakim olacaktır. Düşük sıcaklıkta bu süreç kimyasal kontrollüdür.
Etkin Madde Konsantrasyonun Etkisi: Katı madde-sıvı (akışkan) madde reaksiyonlarında
sıvı fazdaki etkili maddenin artan konsantrasyonu ile mekanizma difüzyon kontrollüden
kimyasal reaksiyon kontrollüye dönüşebilir.Düşük konsantrasyonlarda hız, karıştırma hızına
etkili şekilde bağlıdır (yayınma kontrollü) ve yüksek konsantrasyonlarda hız karıştırmadan
bağımsızdır (kimyasal kont.). Bunun nedeni, etkili maddenin artan konsantrasyonu ile
yayınma hızı, kimyasal reaksiyona yeterli kaynak sağlayacak miktarlara artar ve sonuç olarak
proses yayınma kontrollüden kimyasal kontrollüye değişir.
71
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Katı – Akışkan Reaksiyonlarında Oluşan Ürünün Etkisi
Katı madde, şekilde görüldüğü gibi reaksiyon süresince küçülürse (asitte çözünme gibi), bu
tip reaksiyonlarda akışkandaki etkili maddenin katıya ulaşmasında yani difüzyonda bir
problem olmayacaktır. Bu nedenle mekanizma Kimyasal Reaksiyon Kontrollü olacaktır.
Katı madde reaksiyon süresince küçülmüyor, bir ürüne dönüşüyorsa, reaksiyonun
mekanizması oluşan ürünün karakteristiğine bağlıdır. Oluşan ürün poroz değilse, ürün
akışkanla katı maddenin temasını kesecek ve mekanizma Difüzyon kontrollü olacaktır. Buna
karşılık ürün poroz ise difüzyon olayı gerçekleşebilecek ve mekanizma Kimyasal Reaksiyon
Kontrollü olacaktır.
Katı reaksiyonun ürününün porozitesi ürünün moleküler hacminin reaktanınkine oranıyla
belirlenebilir.
𝑀𝑝 /𝜌𝑝
𝑧 = 𝛼[
]
𝑀𝑟 /𝜌𝑟
Mp : Katı ürünün mol ağırlığı Mr : Katı reaktanın mol ağırlığı
 : Katı ürünün yoğunluğu  : Katı reaktanın yoğunluğu
p
r
 : Stokiometrik faktör
Eğer z < 1 ise ürün, reaktandan daha düşük hacimde oluşacak yani; katı içerisinde porozite
mevcut olacak iken; z > 1 ise ürün, reaksiyona giren katıdan daha yoğun oluşacak yani; yoğun
porozitesiz tabaka oluşacaktır.
72
TAŞINIM OLAYLARI
PROF.DR.KENAN YILDIZ
Örnek 1. Aluminyumun oksidasyonunda z değerini bulunuz.
2Al + 2/3 O2 → Al2O3
𝑧=
1 102/3,97
[
] = 1,28
2 27/2,7
z >1 çıktığına göre reaksiyonda porozitesiz ürün oluşacaktır.
Örnek 2. CaCO3 maddesinin parçalanma reaksiyonunda z değerini bulunuz.
CaCO3 → CaO + CO2
1 56/3,32
𝑧= [
] = 0,457
1 100/2,71
z <1 çıktığına göre reaksiyonda poroziteli ürün (burada CaO) oluşacaktır.
Örnek 3. Piritin oksidasyon reaksiyonunda z değerini bulunuz.
4FeS2 + 11 O2 → 2Fe2O3 + 8SO2
𝑧=
2 160/5,2
[
] = 0,64
4 120/5
z <1 çıktığına göre reaksiyonda poroziteli ürün (burada Fe2O3) oluşacaktır.
Not: Stokiometrik faktör, katı ürünün stokiometrik katsayısının reaksiyona giren katının
stokiometrik katsayısına oranıdır. Örneğin son soruda 2 mol Fe2O3 ürünü oluşması için 4 mol
FeS2 reaksiyona girmektedir. Bu durumda stokiometrik faktör 2/4 dür.
73