Grup içindeki görevim karışık halde gelen ses ve müzik dosyalarını

SES VE MÜZİĞİ AYIRMA
Grup içindeki görevim karışık halde gelen ses ve müzik dosyalarını birbirinden ayırıp ayrı
ayrı elde etmek.Bunun için en çok kullanılan yöntemlerden biri olan independent component
analysis yani kısaca ica’yı seçtim.Yöntemin verimli çalışabilmesi için kaynak işaretlerinin
istatistiksel olarak bağımsız olması gerekmektedir aynı zamanda kaynak işaretlerinden en çok
bir tanesi Gauss dağılımında olmalıdır.
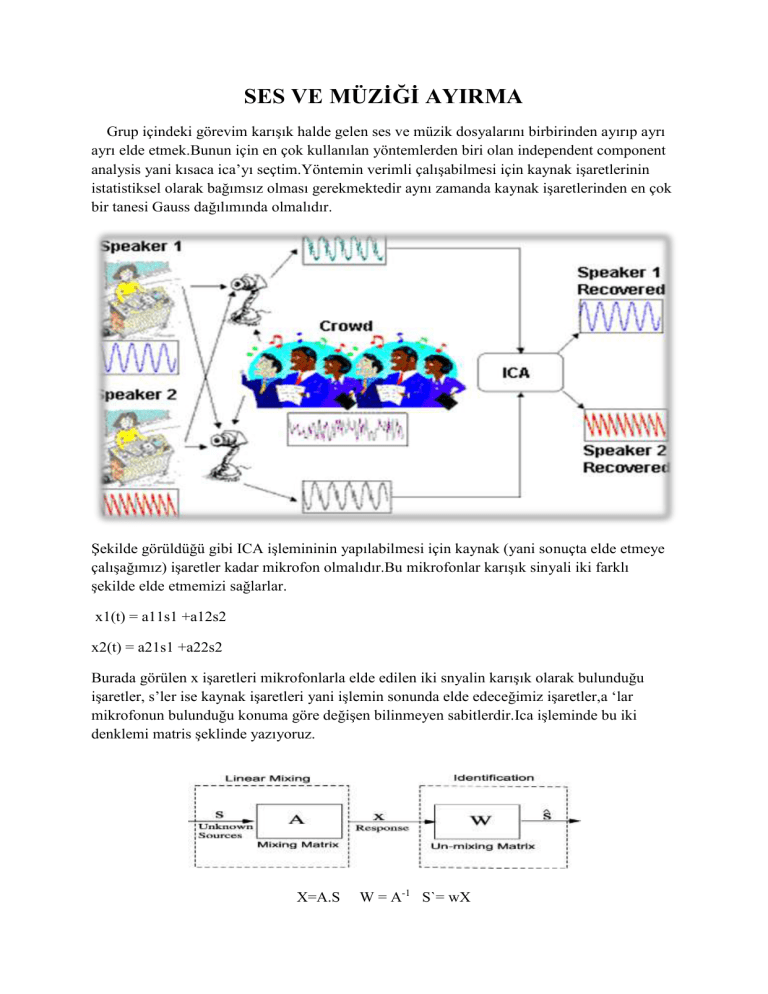
Şekilde görüldüğü gibi ICA işlemininin yapılabilmesi için kaynak (yani sonuçta elde etmeye
çalışağımız) işaretler kadar mikrofon olmalıdır.Bu mikrofonlar karışık sinyali iki farklı
şekilde elde etmemizi sağlarlar.
x1(t) = a11s1 +a12s2
x2(t) = a21s1 +a22s2
Burada görülen x işaretleri mikrofonlarla elde edilen iki snyalin karışık olarak bulunduğu
işaretler, s’ler ise kaynak işaretleri yani işlemin sonunda elde edeceğimiz işaretler,a ‘lar
mikrofonun bulunduğu konuma göre değişen bilinmeyen sabitlerdir.Ica işleminde bu iki
denklemi matris şeklinde yazıyoruz.
X=A.S
W = A-1 S`= wX
Buradaki amacımız tahmini bir w matrisi bularak s kaynağına yaklaşabilmektir. W matrisini
bulabilmek için merkezi limit teoreminden yararlanılır. MLT’ye göre,bağımsız ve aynı
dağılım gösteren rassal değişkenlerin toplamları yaklaşık olarak normal(Gauss) dağılım
gösterir. Ne kadar çok değişken toplanırsa, normal dağılıma o kadar çok yaklaşılır.
Merkezi Limit Teoremi
ICA’nin en bilinen matematiksel çözümü Aapo Hyvärinen tarafından geliştirilen FastIC
algoritmasıdır.Bu algortimaya başlamadan önce bağımsız kaynakların toplamı olup normal
dağılıma yaklaşan x(t) işaretine “whitening” işlemi uygulanır.
X*=ED-1/2ETx=a.s (D x’in diagonal matrisi)
Whitening işleminin ne işe yaradığı bu grafikle anlaşılıyor.
s` = wTx* işleminde sonucun “maximum nongaussianity” olması gerekmektedir çünkü x*
gauss dağılımındayken s’ bir o kadar uzaktır.Bunun için wT nin değeri nongaussianty yi
maksimum yapacak şekilde seçilecektir.
NEGENTROPY YAKINSAMASI
Maximum nngaussianty hesaplamanın en çok kullanılan yoludur.
Aapo Hyv¨arinen, Juha Karhunen, and Erkki Oja’nın kitabından alınmış çözüm.
İterasyon için bu fonksiyonların türevleri alınır.
Çoğu kez a1=1 alınır.
Basit bir şekilde fastICA algoritması şu şekilde yapılır.
1- Başlangıç için w vektörü seçilir
2- w+=>E{xg(wTx)}-E{g’(wTx)}w
3- Yakınsama olmadıysa iterasyona devam edilir, 2ye dönülür.
İşlemin sonunda “w “ normalize edilir.
SES KAYDI;
clear all; close all; clc
recObj = audiorecorder(44100, 16, 2);
get(recObj)
% Record your voice for 5 seconds.
recObj = audiorecorder;
disp('Start speaking.')
recordblocking(recObj, 5);
disp('End of Recording.');
% Play back the recording.
play(recObj);
% Store data in double-precision array.
myRecording = getaudiodata(recObj);
% Plot the waveform.
plot(myRecording);
wavwrite(myRecording,'müzik.wav')
komutuyla bilgisayar üzerinden 2 tane ses kayıt ettim daha sonra bu sesleri farklı
kombinasyonlarla matlabda karıştırdım.Daha sonra bu karışık sesleri aşağıdaki matlab
koduyla ayırdım.
x1=wavread('karışık.wav'); % karıştırılmış ses
x2=wavread('karışık2.wav'); % karıştırılmış ses
soundsc(x1);
soundsc(x2);
figure(3); plot(x1);
figure(4); plot(x2);
N = 1e4;
x=[x1,x2];
W = eye(2,2);
y = x*W;
maxiter=20000;
eta=1;
hs=zeros(maxiter,1);
gs=zeros(maxiter,1);
for iter=1:maxiter
% Get estimated source signals, y.
y = x*W; % wt vec in col of W.
% Get estimated maximum entropy signals Y=cdf(y).
Y = tanh(y);
% Find value of function h.
% h = log(abs(det(W))) + sum( log(eps+1-Y(:).^2) )/N;
detW = abs(det(W));
h = ( (1/N)*sum(sum(Y)) + 0.5*log(detW) );
% Find matrix of gradients @h/@W_ji ...
g = inv(W') - (2/N)*x'*Y;
% Update W to increase h ...
W = W + eta*g;
end;
figure(5); plot(y(:,1));
figure(6); plot(y(:,2));
soundsc(y(:,1));
soundsc(y(:,2));
wavwrite((y(:,1)),'ayrık.wav');
wavwrite((y(:,2)),'ayrık2.wav');
Ek dosyalarındaki ayrık sesler ve grafikler en son karışık seslerden elde ettiğim seslere
ait.Ses.wav müzik.wav ve ilk ses figürleri ise kayıt ettiğim ve daha sonradan elde etmeye
çalıştığım sesler.
Referans:1- Aapo Hyvärinen ve Erkki Oja, Independent Component Analysis:
Algorithms and Applications, Neural Networks Research Centre
Helsinki University of Technology,2000.
2- Demonstration code for "Independent component analysis: A Tutorial Introduction"
JV Stone, MIT Press, September 2004.
Copyright: 2005, JV Stone, Psychology Department, Sheffield University, Sheffield, England.
Raporu yazan;
Çağlayan Tuna
040090298