topoloji - Eastern Mediterranean University

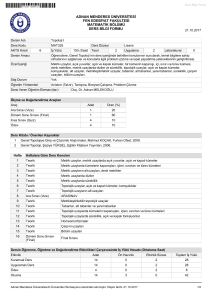
TOPOLOJİYE GİRİŞ
MATE207
DERSİN SAATİ, KREDİSİ,
4, (4+0) saat, 4 kredi / 6 ECTS kredisi, zorunlu meslek dersi
TÜRÜ
DERS YILI, DÖNEMİ
2007-2008 Güz Dönemi
GRUPLAR
01
DERSİN ZAMANI, YERİ
Grup 01: Salı
:08.30 – 10.20 / CL 209
Çarşamba :10.30 – 12.20 / CL 109
DERSİN ÖNKOŞULU
Yok
ÖĞRETİM ELEMANI
Dr. Hüseyin AKTUĞLU
ODA YERİ, NO
Fen Edebiyat Fakültesi, AS 357
GÖRÜŞME SAATLERİ
Pazartesi 10.30 - 11.20
E-POSTA ADRESİ
Huseyin.aktuglu@emu.edu.tr
TELEFON NO
630 12 66
WEB ADRESİ
DERSİN TANIMI
Bu dersin amacı, metrik uzaylar ve metrik uzayların topolojik yapısını incelemek. Topolojik uzayların
özelliklerini çalışmak, Topolojik uzaylarda sürekli fonksiyonlar ve özelliklerini, Çarpım uzaylarını, Kompakt
topolojik uzaylar, Metrik uzayların topolojik yapılarını incelemektir.
ÖĞRENME AMAÇLARI
Bu dersin amacı, öğretmen adaylarının meslek hayatlarında kullanacakları temel bilgileri vermek, üst sınıflarda
alacakları dersler için zemin oluşturmak ve matematiksel düşünce yeteneğini kazandırmaktır. Buna dayalı
olarak, öğrencilerin öğretim sonunda şu amaçlara ulaşmaları beklenmektedir:
 Topolojik uzay kavramı, ince ve kaba topolojiler ile topolojik uzay örneklerini.
 Topolojik uzaylarda açık kapalı küme, kapanış noktası, yığılma noktası, iç nokta, sınır noktası
tanımlarını
 Topolojilerde bazlar, Hausdorff topolojik uzaylar,topolojik uzaylarda yakınsama ve süreklilik
 Çarpım, Bölüm uzayları ve alt uzaylar
 Yakınsama
 Ayırma aksiyomları
 Kompakt,
 Metrik uzay kavramı ve metrik uzayların topolojik yapıları; açık ve kapalı kümeler
Konularını anlamak ve yorumlamak
BAŞARI KOŞULLARI
Öğrencilerin dersle ilgili öğrenmeleri gerçekleştirebilmeleri ve dersten başarılı sayılmaları için şu koşulları yerine
getirmeleri gereklidir:
 Derslere en az %80 oranında devam etme.
 Derslere işlenecek konuyu araştırarak ve okuyarak hazırlıklı gelme.
 Konularla ilgili tartışmalara katılma.
 Konularla ilgili ödevleri yapma.
 Sınavlarda yeterli puanları alma.
ÖĞRETME-ÖĞRENME YAKLAŞIMI
Konuyla ilgili notların aktarılması ve konunun temel noktalarının sınıfta tartışılarak ve ilgili örneklerle pekiştirilek
öğrenilmesi sağlanacaktır. Konunun pozitif bilimlerdeki uygulamarı sunularak, önemi vurgulanacaktır.
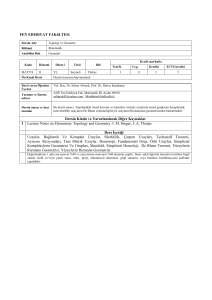
İÇERİK, TAKVİM, ETKİNLİKLER
1. Hafta
Kümeler ve fonksiyonlar ile ilgili temel özellikler.
24 - 28 Eylül
2. Hafta
Topolojik uzaylar, ve Açık kümeler.
1-5 Ekim
3. Hafta
8 - 12 Ekim
Reel sayıların alışılmış topolojisi, Topolojilerin karşılaştırılması,
4. Hafta
15 - 19 Ekim
5. Hafta
22 - 26 Ekim
6. Hafta
30 Ekim-2Kasım
Komşuluk ve Komşuluk ailesi, iç, dış, sınır, Kapanış ve yığılma Noktaları.
7. Hafta
5-9 Kasım
Homeomorfizmalar, Çarpım, bölüm ve alt uzaylar.
8. Hafta
12-15 Kasım
Başlangıç ve sonuç topolojileri, Kalıtsal ve topolojik özellikler.
9. Hafta
16 - 24 Kasım
10. Hafta
26 - 30 Kasım
11. Hafta
3 - 7 Aralık
SINAV HAFTASI
12. Hafta
10-14 Aralık
13. Hafta
17 – 19 Aralık
14. Hafta
24 - 28 Aralık
Kompakt uzaylar, Kompaktlık ve süreklilik,
15. Hafta
Metrik uzaylar
31 Aralık – 1 Ocak
16. Hafta
1 - 5 Ocak
17. Hafta
8 - 22 Ocak
Topoloji Tabanı ve alt taban, Süreklilik, bir noktada süreklilik.
Her noktada süreklilik, açık ve kapalı fonksiyonlar.
Yakınsama, Diziler ve dizilerin yakınsaması.
Ayırma aksiyomları, T0 , T1 ve T2 - uzayları
Lokal kompakt uzaylar, Kompaktlaştırma, Dizisel kompaktlık.
Norumlu uzaylar
Düzgün süreklilik, Cauchy Dizileri, Tam metrik uzaylar.
Final Sınavları
ÖĞRETME-ÖĞRENME YAKLAŞIMI
Konuyla ilgili notların aktarılması ve konunun temel noktalarının sınıfta tartışılarak ve ilgili örneklerle pekiştirilek
öğrenilmesi sağlanacaktır. Konunun pozitif bilimlerdeki uygulamarı sunularak, önemi vurgulanacaktır.
DERS KİTABI
Prof. Dr. Şaziye Yüksel, Genel Topoloji Ders Notları.
OKUMA KAYNAKLARI
Topolojik uzaylar
Prof. Dr. Abdugafur Rahimov, Topolojik Uzaylar
BAŞARI KOŞULLARI
Öğrencilerin dersle ilgili öğrenmeleri gerçekleştirebilmeleri ve dersten başarılı sayılmaları için şu koşulları yerine
getirmeleri gereklidir:
 Derslere en az %80 oranında devam etme.
 Derslere işlenecek konuyu araştırarak ve okuyarak hazırlıklı gelme.
 Konularla ilgili tartışmalara katılma.
 Konularla ilgili ödevleri yapma.
Sınavlarda yeterli puanları alma.
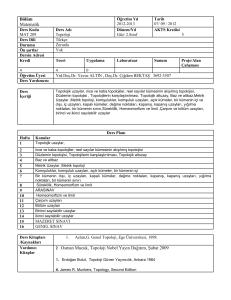
DEĞERLENDİRME
Öğrencilerin dersle ilgili başarı değerlendirmesinde temel alınacak performans öğeleri ve yüzdelik ağırlıkları şöyledir:
I. ara sınavı
:
%30
II. ara sınavı
:
%30
Final
:
%40
Öğrencilerin değerlendirmeye katılan performans öğelerinden elde ettikleri puanlar aşağıdaki çizelgeye göre
nota çevrilecektir:
90-100 = A
60-64 = C
56-59 = C00-39
=F
85-89 = A70-74 = B53-55 = D+
Devamsızlık = NG
80-84 = B+
65-69 = C+
50-52 = D
75-79 = B
60-64 = C
40-49 = D-