Güç Sistemlerinin Bilgisayar Destekli Analizi
326
(7.16) ifadesinde kullanılan V değerinin,
V Vo2 V12 V22 .... Vn2
olduğu unutulmamalıdır.
Örnek olarak akümülatör çıkış gerilimi için =0, bir fazlı yarım dalga
kontrolsüz doğrultucu çıkışındaki gerilim için ise =1.21 değerini
almaktadır. Görüldüğü gibi dalgalılık katsayısı (ya da faktörü) küçüldükçe
(minimum sıfır olabilir) doğru gerilimin kalitesi artmakta, büyüdükçe
azalmaktadır. Bu nedenle doğru gerilim ile beslenen cihaz üreten firmalar
için değeri, doğru gerilimin kalitesini ölçen bir değer olarak kabul edilir.
Doğru gerilim ile beslenen cihazlar için besleme geriliminin kalitesini ölçen
diğer bir katsayı ise şekil katsayısıdır. Şekil katsayısı;
F
V
Vo
(7.17)
eşitliği ile verilir. Örnek olarak akümülatör gerilimi için F=1 değerini alır.
Bir fazlı yarım dalga kontrolsüz doğrultucu çıkışındaki gerilim için ise
F=1.57 değerini almaktadır. Görüldüğü gibi F 1 için doğru gerilimin
kalitesi azalmakta küçüldükçe (minimum 1 olabilir) kalitesi artmaktadır.
Alternatif gerilim ile beslenen cihazlar için besleme geriliminin kalitesini
ölçen önemli bir büyüklük ise distorsiyon (bozulma) faktörüdür. Bu
katsayı;
DF
V 2 V12
V1
(7.18)
olup, harmonik içeren alternatif gerilim içinde ana harmonik (birinci
harmonik) dışında kalan harmoniklerin, ana harmoniğe olan oranını ölçen bir
büyüklüktür. Eğer besleme gerilimi doğru bileşen içermiyor ise ( Vo 0 )
son ifade;
Harmonikler
DF
V 2 V12
V22 V32 .... Vn2
V1
V12
327
(7.19)
olarak ta yazılabilir. İçinde hiçbir harmonik barındırmayan saf bir alternatif
gerilim için DF=0 olacaktır. DF değeri büyüdükçe (maksimum 1 olabilir)
alternatif gerilimin kalitesi azalmakta, küçüldükçe (minimum 0 olabilir)
kalitesi artmaktadır. Piyasada kullanılan elektrikli cihazların çoğunun
alternatif gerilim ile beslendiği düşünülürse, DF katsayısının gerilim
kalitesinin ölçülmesinde ne kadar önemli bir büyüklük olduğu anlaşılacaktır.
7.5. Yük Gerilimi ile Kaynak Akımı Harmonikleri Arasındaki İlişki
Elektrik tesislerinde, yükün uçları arasındaki harmonik bileşenleri ile
doğrultucuyu besleyen kaynak akım harmonikleri arasında çok önemli bir
ilişki bulunmaktadır. Kontrolsüz bir doğrultucunun çıkışındaki (yükün
uçları arasındaki) gerilimin harmonik analizi yapıldığında elde edilen her
harmonik frekansı için, doğrultucunun beslendiği şebekeden çekilen giriş
akımında (alternatif akım) iki harmonik frekansı bulunur. İki frekanstan
biri çıkış geriliminde görülen frekansın bir üst frekansı, diğeri ise bir alt
frekansıdır.
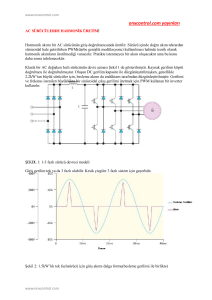
Yukarıda belirtilen olayı daha iyi açıklamak için v(t ) Vm sin wt değerinde
alternatif akım gerilim kaynağından beslenen bir doğrultucu ve bu
doğrultucu çıkışına bağlanmış bir yük olduğu kabul edilsin. Yükün uçları
arasındaki gerilimin harmonik analizi yapıldığında;
v yük (t ) ...... A n sin nwt ....
olduğu görülsün ( v yük (t ) değeri katsayı farkı ile yüke ilişkin i yük (t ) ’ye eşit
olur. Bunun anlamı ise; yük gerilimi harmonik analizinde hangi
harmoniklere rastlanıyor ise yük akımı harmonik analizinde de aynı
harmoniklerle karşılaşılmasıdır. Eğer hesap kolaylığı açısından yük akımı
düzgün kabul edilmiş ise, yük akımı içindeki harmonikler ile yük gerilimi
harmonikleri farklılık gösterecektir). Bu yükü besleyen doğrultucunun
girişine bağlanan alternatif akım şebekesinden çektiği akım i(t) ise bu akımın
harmonik analizi yapıldığında;
328
Güç Sistemlerinin Bilgisayar Destekli Analizi
i(t ) A1 sin wt...... A n1 sin(n 1)wt A n1 sin(n 1)wt ....
harmonikleri ile karşılaşılır. Kısaca, yük geriliminde bulunan her harmonik
için bu yükün alternatif akım şebekesinden çektiği akımda iki harmonikle
karşılaşılır. Bu harmoniklerden ilki yük gerilimindeki harmoniğin bir alt
frekansında, diğeri ise bir üst frekansında olacaktır. İyi bir doğrultma işlemi;
doğrultulan akımın harmonik analizi yapıldığında minimum sayıda harmonik
ile karşılaşılması anlamına geldiğine göre, yukarıdaki açıklamalar aynı
zamanda iyi bir doğrultma işleminin alternatif akım şebekesine minimum
sayıda harmonik yollanması anlamına da gelmektedir. İyi bir alternatif akım
şebekesi ise içinde minimum sayıda (dikkate alınabilir genlikte) harmonik
barındıran şebekedir.
Yukarıda açıklanan ilişkiler iki sayısal örnek ile desteklenebilir. Eğer yük üç
fazlı tam dalga (p=6) kontrolsüz bir doğrultucu çıkışına bağlanmış ise;
v yük (t ) 100 5.7 cos6wt 1.4 cos12wt 0.6 cos18wt .............
olur. Böyle bir yükü besleyen (p=6) doğrultucu, alternatif akım
şebekesinden;
sin 5wt sin 7 wt sin 11wt sin 13wt sin 17 wt
i( t ) I m sin wt
...
5
7
11
13
17
akımını çeker (alternatif akımın iki yönlü olduğu düşünülürse her
harmoniğin yarım periyod süre sonunda şebekeye doğru yöneleceği
unutulmamalıdır). Bu örneğe dikkat edilirse yük gerilimindeki 6. harmonik
için şebeke akımında 5. ve 7. harmonik, yük gerilimindeki 12. harmonik için
şebeke akımında 11. ve 13. harmonik, ... gözlenmektedir. Bu örnekte dikkat
edilmesi gereken diğer bir nokta da; yük gerilimindeki harmoniklerin 6 ve
6’nın katı frekansta olmalarıdır. 6 sayısının doğrultucunun darbe sayısına
(p=6) eşit olduğu gözden kaçırılmamalıdır.
İkinci sayısal örnek 6 faz yarım dalga kontrolsüz doğrultucuya (p=12) ilişkin
olsun. Böyle bir doğrultucunun çıkışına bağlanan yükün harmonik analizi
yapıldığında;
v yük (t ) 100 1.4 cos12wt 0.35cos24wt 0.6 cos36wt .............
Harmonikler
329
elde edilsin. Böyle bir yükü besleyen (p=12) doğrultucu, alternatif akım
şebekesinden;
sin 11wt sin 13wt sin 23wt sin 25wt
i( t ) I m sin wt
.......
11
13
23
25
akımını çeker. Bu örnekte de görüldüğü gibi yük gerilimindeki 12. harmonik
için şebeke akımında 11. ve 13. harmonik, yük gerilimindeki 24. harmonik
için şebeke akımında 23. ve 25. harmonik, ... gözlenmektedir. Harmonik
frekansının harmoniğin genliği ile ters orantılı olduğu da gözden
kaçırılmamalıdır. Örneğin i(t) akımındaki 25. harmoniğin genliği de ana
harmonik genliğinin ( I m ) 1/25 katı olduğu için, harmonik frekansı arttıkça
harmoniklerin (genlik anlamında) etkisi azalmaktadır.
7.6. Harmonikli Bir Yükün Aynı Şebekeye Bağlı Diğer Yüklere Etkisi
Bir doğrultucu harmonik üreten bir kaynak olarak modellenebilir. Bu
doğrultucunun beslendiği alternatif akım şebekesine bağlı bir çok yük
(ör.alternatif akım motorları, lambalar, elektronik cihazlar) bulunmaktadır.
Doğrultucunun bağlandığı alternatif akım barasından (m barası) şebekeye
doğru bakıldığında görülen eşdeğer devre Thevenin modeli ile gösterilebilir
(bkz şekil 7.10). Bu modelde v( t ) ; m barasındaki şebeke gerilimini,
Z th R th jX th ; m barasından şebekeye doğru bakıldığında görülen
eşdeğer empedansı, v th (t ) Vthm sin wt ise m barasından şebekeye doğru
bakıldığında görülen eşdeğer şebeke gerilimini göstermektedir.
Şekil 7.10’da görüldüğü gibi v(t) değeri v th (t ) Vthm sin wt değerinden
farklıdır. Bu farklılığın nedeni ( Z th ) kaynak empedansı üzerinde düşen
V( t ) gerilim düşümüdür. Doğrultucu dolayısı ile i(t) akımı harmonik
içereceğinden, bu akımın Z th empedansı üzerinde meydana getireceği
gerilim düşümü ( V( t ) )’de harmonik içerecektir. Doğrultucu ve diğer
müşterinin bara gerilimi olan v(t);
v th (t ) V(t ) v(t )
ifadesine eşit olduğundan, sinüzoidal bir gerilimden ( v th (t ) ) harmonikli
gerilim olan V(t)’nin çıkarılması ile elde edilen v(t) gerilimi de harmonik
Güç Sistemlerinin Bilgisayar Destekli Analizi
330
içerecektir. v(t) (müşteri) gerilimi harmonikli olduğundan bu gerilimle
beslenen müşteri akımı i1 (t ) ’de harmonikli olacaktır. Müşteri
doğrultucudan uzaklaştıkça ikisinin arasındaki empedans artacağından
i1 (t ) akımı içindeki harmonik genlikleri de azalacaktır.
Diğer
müşteriye
i1 (t )
Z tr
R tr
X tr
v th (t )
m
i yük (t )
i( t )
v( t )
Y
Ü
K
v yük (t )
Şebekenin
Thevenin
Eşdeğeri
Şekil 7.10. Doğrultucunun bağlandığı AA barasından şebekeye doğru
bakıldığında görülen eşdeğer devre Thevenin modeli.
7.7. Harmoniklerin Üretilmesi
Arızasız bir işletmede harmonikler çeşitli sebeplerle ortaya çıkarlar. Bunların
başında lineer olmayan manyetik ve elektrik devreleri gelir. Generatör,
transformatör ve bobin gibi demir çekirdek içeren cihazlarda (aşırı akı
yoğunluğundan dolayı) doymanın meydana gelmesi, demir çekirdeğin lineer
olmayan manyetik devreye dönüşmesi anlamına gelir. Ark fırınlarında
olduğu gibi normal işletme gereği bir arkın oluşması veya yarı iletkenler
kullanılarak sinüzoidal gerilimin şeklinin değiştirilmesi ise elektrik
devrelerinin lineer çalışmamasına örnek olarak verilebilir.
Eğer lineer olmayan devre generatörün manyetik devresi ise generatörün
ürettiği gerilim (sinüzoidal olmaması nedeni ile) harmonikli olacaktır. Eğer
lineer olmayan devre transformatöre ait ise bunun segonder tarafına
bağlanan müşteri gerilimi de harmonikli olacaktır.
Harmonikler
331
Eğer müşterinin manyetik ya da elektrik devresi lineer fakat bu müşteriyi
besleyen gerilim sinüzoidal değil ise, bu müşterinin çektiği akım da
harmonikli olacaktır. Harmonik içeren bir akımın tesis gerilimine nasıl zarar
verdiği bölüm 7.6’da anlatılmıştı.
Sonuç olarak harmonik, ya kaynak tarafındaki harmonikli gerilim etkisinden
(generatörde olduğu gibi) ya da müşterinin lineer olmayan bir devreye
(yarıiletken devre içermesi gibi) sahip olmasından dolayı meydana gelir.
Müşteriyi besleyen gerilim sinüzoidal ve müşteri yükünün karakteristiği
lineer değilse, müşterinin şebekeden çektiği akım harmonikli olacaktır.
Böyle bir yük modellenirken harmonikli akımın, iç empedansı çok büyük
olan bir akım kaynağında üretildiği kabul edilir.
7. 8. Harmoniklerin Enerji Sistemleri Üzerindeki Etkisi
Akım ve gerilim harmoniklerinin güç sistemi içindeki etkilerini dört ana
grup altında toplamak mümkündür;
Paralel ve seri rezonans dolayısıyla harmonik seviyelerinin yükselmesi.
Elektrik üretim, iletim ve tüketiminde verimin azalması.
Elektrik tesislerinde yalıtımı zayıflattığı için tesis elemanlarının
ömürlerinin azalması.
Tesislerde arızalar meydana gelmesi.
Yukarıda sayılan konular çeşitli başlıklar halinde aşağıda açıklanacaktır.
7.8.1. Harmoniklerin Rezonans Etkisi
Elektrik tesislerinde güç faktörünü düzeltmek amacı ile yerleştirilen
kapasiteler, lokal (seri yada paralel) rezonans olayları dolayısıyla yüksek
akımlara maruz kalarak zarar görebilirler.
7.8.1.1. Paralel Rezonans Etkisi
Paralel rezonans durumunda, rezonans frekansında harmonik üreten kaynak
yüksek değerde bir empedansla karşılaşır. Harmonik kaynakları çoğunlukla
akım kaynağı olarak modellendiğinden, paralel kollardan akan harmonik
akımlarında ve paralel kol gerilimlerinde de yükselme olur.
Güç Sistemlerinin Bilgisayar Destekli Analizi
332
Paralel rezonans değişik şekillerde meydana gelir. İlk akla gelen şekli, bir
kapasitenin harmonik üreten kaynakla aynı baraya bağlanması ile ortaya
çıkar. Bu durumda harmonik kaynağı ile kapasite arasında bir paralel
rezonans meydana gelir. Eğer kaynak tümüyle endüktif karakterde ise
rezonans frekansı;
fp f
Ss
Sc
(7.20)
ifadesi kullanılarak hesaplanabilir. Burada f; ana harmonik frekansı, Ss ;
kaynağa ilişkin kısa devre gücü ( VAr ), S c ise kapasitenin nominal görünür
güç değeridir ( VAr ).
Diğer bir paralel rezonans durumu şekil 7.11’de gösterilmiştir.
Sistem barası
Harmonik
üretici
kaynak
D
R şe
L şe
Cşe
A
Şebeke
Yük
CA
B
CB
Yük
Şekil 7.11. Sistemde paralel rezonans durumu.
D tüketicisindeki (harmonik kaynağı) harmonik akımı, sistem barasına
girişte yüksek değerde harmonik empedansı ile karşılaşabilir. Bunun nedeni,
şebekenin selfi L şe ile ya şebekenin kapasitesi Cşe arasında, ya da A
yükünün kapasitesi olan C A (yada C B ) arasında (herhangi bir harmonik
frekansında) paralel rezonans olmasıdır. Rezonansı oluşturan etkiyi anlamak
için, harmonik üreten kaynağın ve her bir yükün (A ya da B) harmonik
akımları, ortak baradaki harmonik gerilimleri ile birlikte ölçülmelidir.
Baradan enerji sistemine doğru akan akım değeri (paralel rezonansta
Harmonikler
333
empedans değeri maksimum olduğu için) küçük ve harmonik gerilimi
yüksek ise genel olarak; enerji sistemi içinde paralel rezonans olduğu
söylenebilir. Eğer yüksek değerde harmonik akımı A yüküne doğru akıyor
ve buradaki harmonik gerilime etki ediyor ise, şebeke selfi olan L şe ile B
yük kapasitesi; C B arasında paralel rezonans vardır (zira akım rezonans
dolayısıyla yüksek değerde olan empedansa doğru değil, düşük değerde olan
empedansa doğru akar).
7.8.1.2. Seri Rezonans Etkisi
Seri rezonans etkisi şekil 7.12’de görülebilir.
Güç
Str (VA )
SC (VAr )
Omik yük
SR (VA)
Şekil 7.12. Seri rezonans etkisi
Yüke paralel olarak bağlanan kapasitenin empedansı yüksek frekanslarda
çok düşeceğinden dolayı omik yük göz önüne alınmayabilir.
Transformatörün selfi ile (güç faktörünü düzeltmek amacı ile yerleştirilen)
kapasite arasında seri rezonans meydana gelebilir. Şekil 7.12’de verilen
devre için yüksek frekanslı harmoniklerde seri rezonans frekansı;
S
S2
f s f tr R
S C z tr S 2
C
(7.21)
formülü kullanılarak hesaplanabilir. Burada f; ana harmonik frekansı, S tr ;
transformatörün nominal gücü, z tr ; transformatörün birim empedans değeri,
SR ; yükün (omik) nominal gücüdür. Seri rezonans devresinde yüksek
değerde kapasite akımları fakat düşük harmonik gerilimleri gözlenir. Akım
devrenin Q kalite faktörüne bağlıdır. Bu değer klasik olarak 500 hz
frekansında 5 olarak alınabilir.
334
Güç Sistemlerinin Bilgisayar Destekli Analizi
Güç faktörünü düzeltmek amacı ile kullanılan kapasitelerin (harmonik
akımlarının etkisi ile oluşan) aşırı yüklenme oranları İngiltere’de %15,
Avrupa’da %30, ABD’de %80 olarak belirlenmiştir.
7.8.2. Dönen Makinalarda Harmonik Etkisi
Harmonik akım ve gerilimleri stator sargılarında ilave kayıplara sebep
olurlar. Aynı etki rotor devresi ile stator ve rotoru oluşturan saç plakalar için
de geçerlidir.
Stator ve rotor sargı uçlarında, harmonik akımlarının oluşturduğu kaçak
alanlar dolayısıyla ekstra kayıplar meydana gelir. Rotor sargısı eğri
yerleştirilen asenkron motorlarda rotor ve statordaki akı değişiklikleri ve
yüksek frekans etkisi, önemli demir kayıplarına neden olur. Kayıp miktarı;
sargı eğriliğine ve saç plakanın demir kayıp karakteristiğine bağlıdır.
Motorun beslendiği şebeke geriliminin sinüzoidal şekilden ayrılma miktarı
(distorsiyon) güç kaybında önemli etkiye sahiptir. Yapılan bir çalışmada
16kW’lık bir motora 60 Hz’lik kaynak frekansında sinüzoidal gerilim
(nominal güçte) uygulanmış ve toplam kayıp 1303 W olarak hesaplanmıştır.
Aynı motora gerilim olarak kare dalga verildiğinde kayıp 1600 W değerine
ulaşmıştır.
Yapılan bir başka çalışmada ise evirici üzerinden beslenen alternatif akım
motorunda harmoniklerin sebep olduğu kayıpların makinenin hangi
bölgesinde ne oranda oluştuğu araştırılmıştır. Buna göre kaybın %14’ü stator
sargısında, %41.2’si rotor sargılarında, %18.8’i sargı uçlarında, %25.8’i
ise diğer bölgelerde oluştuğu saptanmıştır. Bu çalışmada hangi harmonik
etkisinin bu kayba neden olduğu ve başka bir makinede kayıpların nasıl
olacağı belirtilmemekle beraber ana kaybın rotorda ortaya çıktığı kesindir.
Harmonik etkisi ile ortaya çıkan ilave güç kaybı alternatif akım makineleri
için ciddi etkilere sahiptir. Makinenin ekstra harmonik akım etkilerine
dayanması, ilave kayıpları karşılayabilme kapasitesine bağlıdır. Sincap
kafesli asenkron motorun rotoru, rotoru sargılı olana oranla sıcaklığa
dayanımı daha fazladır. Generatörlerde ters akım bileşeni %10 ile
sınırlandırılmıştır. İndüksiyon motorlarında ise gerilimin ters bileşeni %2 ile
sınırlıdır. Bu değerlerin aşılmasını sağlayan harmoniklere müsaade
edilmemiştir. Alternatif akım makina statorundaki harmonik akımları
harmonik alan hızına bağlı olarak doğru alan yönünde makina milinde
moment üretirler. Ters alan yönündeki harmonikler de ters moment üretirler.
Harmonikler
335
Harmonik etkileri ortalama moment üzerinde etkili olsalar da çoğu durumda
ihmal edilirler. Ortalama moment üzerinde etkili olabilen harmonikler,
önemli ölçüde moment pulzasyonları meydana getirirler.
7.8.3. Elektrik Tesislerinde Harmonik Etkisi
Harmonik akımlarının elektrik devreleri üzerinde iki önemli etkisi vardır.
Harmonik akımları toplam akımın etkin değerini artırdığı için iletim
ortamının;
Pilave I 2n R n
n 2
(7.22)
ifadesi ile hesaplanan ilave güç kayıpları olacaktır. Burada I n ;n.
harmonik akımın etkin değeri, R n ise bu harmonik frekansındaki sistem
direncidir.
Harmonik akımları yüzünden enerji nakil hatlarına ilâve olarak
makinalar ve tranformatörler de ısınırlar. Ayrıca generatörlerin
amortisman sargıları, bir fazlı veya iki fazlı kısa devrelerde meydana
gelen harmonikleri azaltacak ve ortadan kaldıracak şekilde etki ederken,
kendileri de çok ısınırlar ve generatörlerde ilâve kayıplar meydana
gelmesine yol açarlar.
Harmonik akımları çeşitli devre empedansları üzerinde ilave gerilim
düşümlerine neden olurlar. Harmonik akımlarının frekansları, normal
şebeke frekansı 50 Hz'in katlarına eşit olduğundan, bu akımlar
karşısında generatör, transformatör ve hat reaktansları üzerinde meydana
gelen gerilim düşümleri de harmonik frekansları ile orantılı olarak artar
ve sonuç olarak gerilimin dalga şekli bozulur. Meselâ ark ocakları gibi
olayların hızlı değiştiği yerlerde, harmonik akımlarının yol açtıkları
gerilim düşümleri de zamana bağlı olarak hızlı değiştiğinden, şebeke
geriliminde 2- 15 Hz mertebesinde titreşimler baş gösterir (flicker olayı).
Bu olay yakında bulunan tesislerdeki cihazlara ve aydınlatma cihazı
kullanan tüketicilerine olumsuz şekilde etki yapar.
336
Güç Sistemlerinin Bilgisayar Destekli Analizi
Hata noktasından bakıldığında yüksek empedanslı, dolayısıyla düşük hata
akımlı sistemlerde (ki bunlar zayıf sistemler olarak adlandırılır) harmonik
akımlarının oluşturacağı gerilim düzensizlikleri, düşük empedanslı yüksek
akımlı sistemlere (ki bu sistemler kuvvetli sistemler olarak adlandırılır)
oranla daha çok olacaktır.
Kablo ile yapılan iletim sistemlerinde ise harmonik gerilimleri, tepe
değerlerine bağlı olarak, kabloda dielektrik zorlanmayı artırıcı etki yaparlar.
Bu yüzden kablonun ömrü azalır. Hata sayısı arttıkça onarım masrafları da
artar. Sinüs şeklindeki gerilim eğrisine eklenen gerilim harmoniklerinin
meydana getirdiği iğne ucu şeklinde sivri, çok kısa süreli ani gerilim
yükselmeleri,
meselâ gerilim rezonansı gibi hallerde, makina ve
transformatör sargılarının izolasyonu ve kondansatörlerin dielektrik maddesi
için büyük bir tehlike teşkil eder ve hatta izolasyonda delinmeye yol
açabilirler. Buna karşılık mesnet, askı ve geçiş izolatörleri için bu gibi aşırı
gerilimler hemen hemen hiç bir tehlike yaratmazlar. Normal frekanslı
gerilim üzerine bindirilmiş olan harmonik gerilimlerinin kısa süreli, iğne
şeklinde ani yükselen uçları izolatörlerde olduğu gibi yarı iletkenlerin de
delinmesine sebep olurlar.
Transformatörlerde ise harmonik gerilimleri histerizis ve girdap akımlarını
artırarak kayıpları büyütür ve yalıtımı zorlar. Harmonik akımları bakır
kayıplarını da artırır. Bu durum özellikle çevirici transformatörlerinde önem
kazanır. Zira harmonikleri süzmek için kullanılan filtreler alternatif akım
tarafına bağlanır, dolayısıyla harmonik generatörleri olarak kabul
edebileceğimiz doğrultucu devrelerin ürettiği harmonikler, filtreye girmeden
önce çevirici transformatörünün üzerinden akarlar. Bu yüzden
transformatörün gücü artırılmalıdır (bu ise transformatörün maliyetini
artırır). Ayrıca çevirici transformatörü tankı üzerinde ısınmış noktalar
meydana gelir.
Güç transformatörlerinde 3’ün katı harmonikler (sıfır bileşen devreye ilişkin)
üçgen sargı içinde dolaşırlar. Eğer transformatör dizaynında bu etki
düşünülmemiş ise bu etki önemsenmeli ve tedbir alınmalıdır.
Eğer transformatör asimetrik bir yükle yüklenirse, yük akımının doğru akım
bileşeni içermesi durumunda transformatörün manyetik devresi doymaya
gidecektir ve uyarma akımının tüm harmonik bileşen seviyeleri artacaktır.
Kapasiteler üzerindeki gerilimin değişime uğraması (bozulması) kapasitenin;
Harmonikler
337
2
C(tan ) w n Vn
n 1
(7.23)
formülü ile ifade edebilecek ekstra güç kaybının artmasına neden olur.
Burada, tanδ = R / ( 1/ ωC ) ile hesaplanan kayıp faktörü, w n =2π f n , Vn ; n.
harmonik geriliminin etkin değeridir.
Dikkat edilmesi gereken bir diğer önemli nokta da; kapasitenin ana
harmoniğinde ürettiği Q1 reaktif gücünü içeren;
Q Qn
n 1
(7.24)
toplam reaktif güç değerinin kapasitenin nominal reaktif güç değerini
aşmaması gerektiğidir. Daha önce de belirtildiği gibi şebeke ve kapasite
arasında meydana gelen seri ve paralel rezonans yüzünden oluşan aşırı
gerilim ve yüksek akım harmonikleri kapasiteleri ısıtır ve hatta tahrip
ederler.
7.8.3. Röleler Üzerinde Harmonik Etkisi
Harmonikler rölelerin çalışma karakteristiklerini bozma veya tahrip etme
özelliğine sahiptir. Dijital röleler ve yazılımları, örneklenmiş data bilgisine
ve sıfır geçişlerine çok duyarlıdır. Bu yüzden harmonik etkileri röleleri hata
yapmaya meyilli bir duruma sokarlar.
Yukarıda (harmoniğin bozucu özelliği dolayısıyla) belirtilen olumsuz etki
çoğu durumda röle çalışma karakteristiğini önemli miktarda değiştirmemekte
ve ciddi bir problem meydana gelmemektedir.
Harmonik gerilim seviyesinin % 20’den az olduğu durumlarda (yapılan
testlerden) çoğunlukla olumsuz sonuç alınmamıştır. Fakat gelecekte güçlü
çeviricilerin varlığı dolayısıyla bu durumun değişmesi kuvvetle muhtemel
görülmektedir. Bu konuyu iki ana başlık altında incelemekte fayda vardır.
338
Güç Sistemlerinin Bilgisayar Destekli Analizi
7.8.4.1. Sistemdeki Hata Sonucunda Ortaya Çıkan Harmonik
Problemleri
Rölelerin koruma fonksiyonları çoğunlukla ana harmonik akım (veya
gerilim) değeri gözetilerek veya hata oluştuğunda diğer harmoniklerin filtre
edildiği kabulü ile (sonuç olarak) ana harmonik dışındaki harmoniklerin
ihmal edildiği bir sisteme göre gerçekleştirilir. Bu kabul özellikle aşırı akım
korumasında kullanılan elektromanyetik röleler için geçerlidir.
Elektromekanik röleler ise yapıları gereği yüksek dereceden harmoniklere
karşı daha az duyarlıdır.
Empedans ölçümünde harmonik etkileri oldukça önemlidir. Mesafe röleleri
(bunlar hat empedansını ölçerek çalışırlar) ana frekansa tekabül eden
empedans değerinin ölçülmesi üzerine bina edilen çalışma ilkesine sahiptir.
Hata meydana geldiğinde özellikle 3.harmonik etkisi ile ölçüm hatası
meydana gelebilir.
Direnç üzerinden meydana gelen kısa devrelerde akım yüksek değerde bir
direnç üzerinden akacağı için yüksek harmonik bileşenleri ortaya çıkacaktır.
Bu durumda büyük bir olasılıkla rölenin görev yapmasına imkan olamaz (bu
tür hatada toprak empedansının değeri önemlidir).
Eğer hata (kısa devre) bir direnç üzerinden olmayıp metalik kısa devre ise
akım ve gerilim ana harmonikleri önem kazanır. Akım transformatörlerinde
meydana gelen doyma dolayısıyla akım trafosu segonder akımında (rölenin
beslendiği akım) bozulma meydana gelir.
Segonder sargıda yüksek değerde (sürekli halde) bir elektromotor kuvvet
oluştuğunda, röle transformatörünün uyarma empedansından akan lineer
olmayan akım, tek mertebeden harmonik distorsiyona neden olur. Çekirdek
doyuma ulaştığında, (geçici halde) harmonik üretim kaynağı, röle
transformatör geriliminin ikinci ve üçüncü harmonik bileşenleri olacaktır.
Yukarıda bahsedilen dizayn problemlerinden sistem gereksinimlerini
karşılayan doğru cihaz seçimi yapılarak kaçınmak mümkündür. Özellikle
dijital koruma sistemlerine sahip mesafe koruma esaslı sistemlerde, akım ve
gerilim dalga şekillerinin filtre edilmesi oldukça önemlidir.
Harmonikler
339
7.8.4.2. Hata Koşulları Dışında Harmonik Problemleri
Normal sistem koşullarında koruyucu cihazların duyarsızlığı, bizlere, hata
koşulları dışında güç sistemindeki harmoniklerin herhangi bir probleme
sebep olmadığını ifade eder gibidir. Güç transformatörlerinde, pratikte,
transformatörün devreye girmesi sırasında, mıknatıslanma devresinden
kaynaklanan mıknatıslanma akımının ilk anlardaki değeri, yüksek harmonik
bileşenlere sahiptir. Bu bileşen değerleri ortaya çıktığında, transformatörü
koruyan sistemler devreye girerek (hatalı bir durum olmadığını belirleyerek)
devre kesicisini açmasını engeller. Zira enerjilenme esnasında çok yüksek
genlikte akımlar dolayısı ile röle hata işareti verme eğilimindedir. Bu durum
herhalde harmoniklerin faydasını gösteren sayılı örnekler içinde yer alır.
7.8.5. Tüketici Cihazlarında Harmonik Etkileri
Harmonikler, televizyon alcılarında tepe gerilim değerine etki ederek
görüntünün büyüklüğünü ve ışık şiddetini değiştirir.
Floresan ve civa arklı lambalarda, balastlar kapasite içerirler. Gerek
devrenin gerekse balastın endüktansı ile bu kapasite arasında bir
rezonans meydana gelebilir. Bu durumda aşırı ısınma ve hata oluşumu
söz konusudur.
Bilgisayar imalatçıları harmonik distorsiyonu için limit değerler
vermişlerdir. Örneğin harmonik oranı Honeywell firması için % 3, IBM
için % 5’den az olmalıdır.
Tristör kullanılan hız kontrol devrelerinde harmonik gerilimleri,
tristörlerin zamanından önce tetiklenmesine veya tetiklenmeyen
tristörlerin bozulmasına yol açar. Çeşitli cihazlar arasındaki rezonans
etkisi aşırı gerilim ve dalgalanmalara yol açar.
Yukarıda sayılan problemler aynı baraya bağlı diğer tüketicilere
yansıyabilir. Etkileşim merkezleri arasındaki mesafe arttıkça problem
azalır.
Mikroişlemci ile kontrol edilen sistemlerde harmonikler işlemcinin
besleme devresine girerek hatalı çalışmasına yol açarlar. Bu nedenle
pratik uygulamalarda mikroişlemcilerin besleme devrelerinin şebekeden
bağımsız olarak güç kaynakları üzerinden yapılması veya hassas filtre
kullanılması, hatalı çalışmalarını önlemek açısından çok önemlidir.
340
Güç Sistemlerinin Bilgisayar Destekli Analizi
7.8.6. Güç Ölçen Aletlerde Harmonik Etkisi
Ölçü aletleri saf sinüzoidal akıma göre kalibre edilirler. Bu aletlere
uygulanan distorsiyonlu işaretlerde hata yapma ihtimalleri yüksektir.
Harmonik güç akışının yönü, fabrika sayaçlarının doğru ölçüm yapmaları
açısından oldukça önemlidir. Yapılan çalışmalar göstermiştir ki, ölçü
aletlerinin yapısına bağlı olarak harmonik etkiler dolayısıyla, hem pozitif
hem de negatif yönde ölçme hataları ortaya çıkmaktadır.
Enerji ölçen sayaçlarda kullanılan ölçü aleti Ferraris motorudur. Bu motor
elektromagnetik dizayn üzerine kurulmuştur. Rotorda (gerek hızlanma
gerekse yavaşlama için) oluşan moment rotora yollanan akı ile temin edilir.
Yataklamalardan kaynaklanan sürtünme hatalarını önlemek için ayrıca bir
(ikincil ) akı üretimi söz konusudur. Her iki amaca dönük (moment için) akı
üreten elemanlar genlik ve frekansa nazaran lineer olmayan özelliktedirler.
Güç ölçen bir ölçü aletine etki eden toplam güç miktarı;
P PT Pda PF PH Vda I da VF I F cos F VH I H cos H (7.25)
ifadesi ile hesaplanabilir. Ölçü aleti Pda gücünü ölçmeyecektir fakat bu
gücün etkisine karşı duyarlıdır. Bu alet frekans ölçümünden kaynaklanan
hatadan dolayı PF değerini tam olarak PH değerini ise yanlış olarak
ölçecektir. Toplam harmonik gücü olarak adlandırılan PH değeri ana
harmoniğin altındaki ve üstündeki frekanslardaki akım ve gerilim değerinin
çarpımının toplanmasıyla elde edilir.
Doğru akım gücü olan Pda hata miktarı Pda / PT oranına bağlıdır. Hatanın
işareti ise güç akışının yönüne bağlıdır. Benzer olarak harmonik gücünün
ölçülmesinde K PH / PT ile orantılı bir hata ortaya çıkar. K değeri ölçü
aletinin frekans cevap karakteristiğine, hatanın işareti ise güç akış yönüne
bağlı olarak değişir.
Doğru akım gücü, harmonik akım ve gerilimleri tek başlarına moment
üretmezler. Fakat bunlar ana frekansın ürettiği güç kapasitesini azaltıcı etki
yaparlar. Doğru akım çalışma akışını bozar, değiştirir, magnetik elemanların
Harmonikler
341
geçirgenlik artışını değiştirir. Harmonik akımlarının ürettiği akılar ikinci bir
moment oluşturarak ölçümde hatalara neden olur.
7.8.7. Güç Faktörü Üzerine Harmonik Distorsiyonu Etkisi
n; hem gerilimin hem de akımın sahip olduğu harmonikleri, m; yalnızca
gerilim dalga şeklinde bulunan harmonikleri, p; yalnızca akım dalga şeklinde
görülen harmonikleri simgelemek üzere, genel olarak harmonikli gerilim ve
akımın ani değer ifadesi için;
n
m
v( t ) 2Vn sin( nwt n ) 2Vm sin( mwt m )
n
(7.26)
p
i( t ) 2I n sin( nwt n n ) 2I p sin( pwt p )
(7.27)
yazılabilir. (7.26) ve (7.27) eşitlikleri ile verilen gerilim ve akıma sahip olan
kaynağa ilişkin güç faktörü (GF);
n
1T
Vn I n cos n
v( t )i( t )dt
T
GF 0
1/ 2
VI
n 2 m 2 n 2 p 2
( Vn Vm )( I n I p )
(7.28)
olur. Eğer gerilim saf sinüzoidal ( V V1 ) ise son eşitlik;
V I cos 1 I1
GF 1 1
cos 1 cos 1
V1I
I
(7.29)
olur. V ve I değerleri gerilim ve akıma ilişkin etkin değerler olup, cos1 ise
displacement faktör adı verilir ( 1 ;gerilim ve akımın ana harmonikleri
arasındaki faz farkıdır). ise akım distorsiyon faktörüdür. =1 olmadan güç
faktörü bir değerine ulaşamaz .
Güç Sistemlerinin Bilgisayar Destekli Analizi
342
Genellikle kayıpsız elemanlar güç faktörünün iyileştirilmesinde
kullanıldığından, görünür gücün minimum kılınması, optimum güç faktörü
elde edilmesine bağlıdır. Örneğin (7.26) ve (7.27) ifadeleri ile ani gerilim ve
akımı verilen kaynağa paralel olarak bir C kapasitesi bağlanırsa, görünür
gücün C kapasitesine bağlı olarak ifadesi;
1/ 2
m
n
2
S Vn2 Vm
m
2 2 2 2
Vm m w C
n 2
2 2 2 2
(I n Vn n w C 2Vn I n nwC sin n
I 2p
m
1/ 2
(7.30)
olur. Son ifadenin C’ye göre türevi alınır ve sıfıra eşitlenirse, optimum
kapasite;
C opt
1 n
Vn nI n sin n
w
n
2 2
Vn n
m
(7.31)
2 2
Vm
m
olarak bulunur. Yukarıdaki ifadeden de görüldüğü gibi harmonikli akım ve
gerilim üreten bir kaynakta tek bir kapasite kullanarak GF=1 yapmak
mümkün değildir. Böyle bir sistemde en verimli kompanzasyona ancak
(7.31) ifadesinde verilen Copt değerinde bir kapasite kullanılarak
ulaşılabilir.
Eğer, faz arası gerilim harmonik ihtiva ederse, kompanzasyonlu şebekelerde
bir toprak teması (hata) halinde, toprak akımlarında o kadar büyük
harmonikler bulunur ki, yıldız noktasına bağlı kompanzasyon bobini
görevini tam olarak yapamaz ve arkın söndürülmesi zorlaşır.
Kompanzasyonsuz şebekelerde ise sık gelip giden toprak kısa devresi,
işletme frekansından daha yüksek frekanslı aşırı gerilimlerin meydana
gelmesine sebep olur; zira arkın her sönüp ve yeniden tutuşmasında, şebeke
frekanslı cebri titreşimlere yol açar.