SORULAR
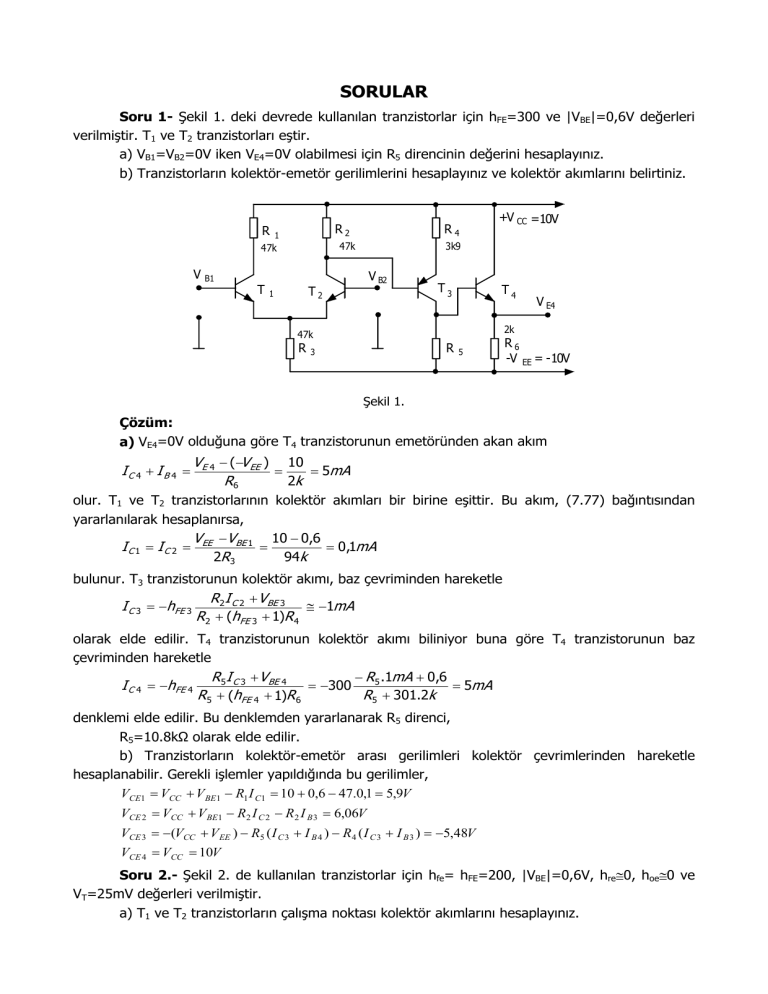
Soru 1- Şekil 1. deki devrede kullanılan tranzistorlar için hFE=300 ve |VBE|=0,6V değerleri
verilmiştir. T1 ve T2 tranzistorları eştir.
a) VB1=VB2=0V iken VE4=0V olabilmesi için R5 direncinin değerini hesaplayınız.
b) Tranzistorların kolektör-emetör gerilimlerini hesaplayınız ve kolektör akımlarını belirtiniz.
R
R2
1
47k
47k
V B1
T
R4
3k9
V B2
T2
1
T3
T4
V E4
2k
47k
R
+V CC =10V
R
3
5
R6
-V EE = -10V
Şekil 1.
Çözüm:
a) VE4=0V olduğuna göre T4 tranzistorunun emetöründen akan akım
IC 4 + I B 4 =
VE 4 − (−VEE ) 10
=
= 5mA
R6
2k
olur. T1 ve T2 tranzistorlarının kolektör akımları bir birine eşittir. Bu akım, (7.77) bağıntısından
yararlanılarak hesaplanırsa,
V −VBE 1 10 − 0,6
I C 1 = I C 2 = EE
=
= 0,1mA
2R 3
94k
bulunur. T3 tranzistorunun kolektör akımı, baz çevriminden hareketle
R 2I C 2 + V BE 3
≅ −1mA
I C 3 = −hFE 3
R 2 + (hFE 3 + 1)R 4
olarak elde edilir. T4 tranzistorunun kolektör akımı biliniyor buna göre T4 tranzistorunun baz
çevriminden hareketle
− R 5 .1mA + 0,6
R 5I C 3 + V BE 4
= −300
= 5mA
I C 4 = −hFE 4
R 5 + (hFE 4 + 1)R 6
R 5 + 301.2k
denklemi elde edilir. Bu denklemden yararlanarak R5 direnci,
R5=10.8kΩ olarak elde edilir.
b) Tranzistorların kolektör-emetör arası gerilimleri kolektör çevrimlerinden hareketle
hesaplanabilir. Gerekli işlemler yapıldığında bu gerilimler,
VCE1 = VCC + VBE1 − R1 I C1 = 10 + 0,6 − 47.0,1 = 5,9V
VCE 2 = VCC + V BE1 − R2 I C 2 − R2 I B 3 = 6,06V
VCE 3 = −(VCC + V EE ) − R5 ( I C 3 + I B 4 ) − R4 ( I C 3 + I B 3 ) = −5,48V
VCE 4 = VCC = 10V
Soru 2.- Şekil 2. de kullanılan tranzistorlar için hfe= hFE=200, |VBE|=0,6V, hre≅0, hoe≅0 ve
VT=25mV değerleri verilmiştir.
a) T1 ve T2 tranzistorların çalışma noktası kolektör akımlarını hesaplayınız.
2
b) Devrenin Vo /Vi gerilim kazancını ve ri giriş direncini hesaplayınız.
22k
R2
R3
Vi
ri
C
1
12k
C2
1k
C
T2
T1
Ry
3
Vo
20kΩ
R6
R1
100k
+12V
R5
300Ω
R4
12k
R7
4k7
C4
-12V
Şekil 2.
Çözüm:
a) T1 tranzistorunun çalışma noktası kolektör akımı için baz çevriminden hareketle
VCC +VBE 1
I C 1 = −hFE 1
= −0,482mA
re 1 = 51,9Ω
R1 + (hFE 1 + 1)(R 2 + R 3 )
değeri elde edilir. IC1 bilindiğine göre T2 tranzistorunun çalışma noktası kolektör akımı için
R 4 I C 1 + V BE 2
I C 2 = −hFE 2
= 1,02mA
re 2 = 24,51Ω
R 4 + (hFE 2 + 1)(R 6 + R 7 )
değeri elde edilir.
b) Kaskat kuvvetlendiricinin gerilim kazancı katların kazançlarının çarpımına eşittir. Buna
göre T2 den oluşan ortak emetörlü devrenin gerilim kazancı için
R y′ 2
R 5 // R y
7500
Kv 2 = −
=−
=−
= −23,1
re 2 + R 6
re 2 + R 6
324 ,51
değeri elde edilir. T2’den oluşan devrenin giriş direnci,
ri 2 = hfe 2 (re 2 + R 6 ) = 64 ,9kΩ
olarak elde edilir. T1 tranzistorunun kolektöründeki eşdeğer direnç R′y = ri2//R4
dir. T1 tranzistorunun sağladığı gerilim kazancı,
R y′ 1
r // R 4
10127
= − i2
=−
= −9,63
Kv1 = −
51,9 + 1000
re 1 + R 3
re 1 + R 3
olarak elde edilir. Kaskat kuvvetlendiricinin gerilim kazancı
K v = K v 1K v 2 = −23,1.(−9,63) ≅ 222 ,45
olur. Devrenin giriş direnci için ri=R1//hfe1(re1+R3)= 100kΩ//210,38≅67,8kΩ değeri elde edilir.
Soru 3.- Şekil 3.de kullanılan tranzistorlar için hfe=hFE=250, hre≅0, hoe≅0, |VBE|=0,6V ve
VT=25mV değerleri verilmiştir.
a) Tranzistorların çalışma noktası kolektör akımlarını hesaplayınız.
b) Vo/Vi gerilim kazancını, ri giriş direncini ve ro çıkış direncini hesaplayınız.
Çözüm:
T1 tranzistorunun çalışma noktası akımı için baz çevriminden hareketle,
VCC + V BE 1
I C 1 = −hFE 1
= −0,2mA
re 1 = 12,5Ω
R1 + (hFE 1 + 1)(R 2 + R 3 )
değerine varılır. T2 tranzistorunun baz çevriminden hareketle kolektör akımı için
3
I C 2 = −hFE 2
R 4 I C 1 + V BE 2
= 0,936mA
R 4 + (hFE 2 + 1)(R 6 + R 7 )
re 2 = 26,71Ω
elde edilir. T3 tranzistorunun baz çevriminden hareketle kolektör akımı için
V + VEE − R5I C 2 −V BE 3
I C 3 = hFE 3 CC
= 3,98mA
re 3 = 6,28Ω
R5 + (hFE 3 + 1)R 8
bulunur.
b) Kaskat kuvvetlendiricinin kazancı katların kazançlarının çarpımına eşittir. T3 den oluşan
emetör çıkışlı devrenin gerilim kazancı için
Kv 3 =
R 8 // R y
Re 3
1875
=
=
= 0,997
re 3 + Re 3 re 3 + (R 8 // R y ) 6,28 + 1875
olur. T3’den oluşan devrenin giriş direnci ri3=hfe3(re3+Re3)=470,3kΩ dir. T1’den oluşan ortak
emetörlü kuvvetlendirici devrenin gerilim kazancı,
12k
56k
C2
+
R3
C1
ri
T3
T1
100k
+
Vo
R6
R 8 ro
300Ω
R1
C4
T2
560Ω
Vi
+V CC =12V
R5
R2
R7
R4
4k7
27k
3k
Ry
5kΩ
C3
-V EE = -12V
Şekil 3.
Kv 2 = −
R 5 // ri 3
= −35,82
re 2 + R 6
değerinde bulunur. T2’den oluşan devrenin giriş direnci ri2=hfe2(re2+R6)=81,68kΩ
dir. Ortak emetörlü kuvvetlendirici olan T1’den oluşan devrenin gerilim kazancı,
R // r
K v 1 = − 4 i 2 = −29,62
re 1 + R 3
olur. Kaskat kuvvetlendiricinin gerilim kazancı katların kazançlarının çarpımına eşittir. Bulunan
kazanç değerleri kullanıldığında
Kv=Kv1Kv2Kv3≅1058 olur. Devrenin giriş direnci R1//r′i1=R1//hfe1(re1+R3)
bağıntısı ile hesaplanır. Değerler yerine konduğunda ri=100//171,25≅63kΩ bulunur. Çıkış direnci
emetör çıkışlı kuvvetlendiricinin çıkış direncidir. Buna göre devrenin çıkış direnci,
ro = (re 3 +
R5
) // R 8 = 54,28 // 3000 = 53,3Ω olur.
hfe 3
Soru 4.- Şekil 4 de kullanılan tranzistorlardan T1 ve T2 eştir. Tranzistorlar için hfe=hFE=250,
|VBE|=0,6V, hre≅0, hoe≅0 ve VT=25mV değerleri verilmiştir.
a) Tranzistorların çalışma noktası kolektör akımlarını hesaplayınız.
b) Vo/Vi gerilim kazancını, ri giriş direncini ve ro çıkış direncini hesaplayınız.
4
12V
3k6
C
R2
R4
91k
91k
R6
R7
1
T1
Vi
100k
T3
T2
T4 C 3
Vo
R5
R1
ri
C2
200Ω
110k
100k
R3
13k
R8
R9
3k
Ry
ro
20kΩ
-12V
Şekil 4.
Çözüm:
T1 ve T2 tranzistorları eş tranzistorlardır ve bazlarına bağlanan R1 ve R5 dirençleri de eşittir.
Buna göre sükûnet halinde (Vi=0 iken) kolektör akımları eşit olacaktır. T1’in baz çevriminden
hareketle T1 ve T2 tranzistorlarının kolektör akımı için
V EE − V BE 1
I C 1 = I C 2 = hFE 1
≅ 0,052mA
re 1 = re 2 = 481Ω
R1 + 2(hFE 1 + 1)R 3
olarak bulunur. T3 tranzistorunun baz çevriminden hareketle T3’ün kolektör akımı için
R 4 I C 2 + V BE 3
I C 3 = −hFE 3
≅ −0,99mA
re 3 = 25,3Ω
R 4 + (hFE 3 + 1) / R 6 + R 7 )
bulunur. T4 tranzistorunun kolektör akımı için
R 8I C 3 + V BE 4
I C 4 = −hFE 4
= 4mA re 4 = 6,25Ω
R 8 + (hFE 4 + 1)R 9
bulunur.
b) Kaskat kuvvetlendiricinin gerilim kazancı, katların kazançlarının çarpımına eşittir. T4
tranzistoru emetör çıkışlı bir kuvvetlendirici olarak çalışmaktadır. Bu kuvvetlendiricinin gerilim
kazancı için
Kv 4 =
R 9 // R y
Re 4
2609
=
=
= 0,998
re 4 + Re 4 re 4 + (R 9 // R y ) 6,25 + 2609
bulunur. T4’den oluşan emetör çıkışlı devrenin girişinden görülen direnç,
ri 4 = hfe 4 (re 4 + R e 4 ) = 654 kΩ
olarak hesaplanır. T3 tranzistorunun kolektöründeki değişken işaret yükü, R8//ri4 dür. Buna göre
ortak emetörlü bir kuvvetlendirici olan bu devrenin sağladığı gerilim kazancı,
R // r
12747
Kv 3 = − 8 i 4 =
= −56,6
re 3 + R 7 25,3 + 200
bulunur. T3 tranzistorunun bazından görülen direnç,
ri 3 = h fe 3 ( re3 + R7 ) = 56,3kΩ
olur. T1 ve T2 den oluşan uzun kuyruklu devrenin sağladığı gerilim kazancı,
R 4 // ri 3
34781
=
= 25,5
Kv 2 =
R
1362
2re 2 + 5
hfe 2
5
dir. Kaskat kuvvetlendiricinin gerilim kazancı, katların kazançlarının çarpımına eşittir. Buna göre,
K v = K v 2K v 3K v 4 = −1440
olacaktır. Devrenin giriş direnci,
ri = R1 //(2hfe 1re 1 + R 5 ) = 77 ,3kΩ
dir. Devrenin çıkış direnci, emetör çıkışlı kuvvetlendirici olan T4 tranzistorunun emetöründen
görülen dirence eşittir. Buna göre
ro = (re 4 +
R8
) // R 9 = 58,25 // 3kΩ ≅ 57Ω
hfe 4
olur.
Soru 5.- Şekil 5.de kullanılan tranzistor için hFE=250, VBE=0,6V, hre≅0, hoe≅0 ve VT=25mV
değerleri verilmiştir.
a) Tranzistorların çalışma noktasında kolektör akımlarını hesaplayınız.
b) Vo /Vi gerilim kazancını, ri giriş direncini ve ro çıkış direncini hesaplayınız.
8k2
130k
T2
C
T1
Vi
ri
+V CC =15V
R3
R1
R2
16k
Vo
R4
R5
1k
3k
ro
Şekil 5.
Ic1
Çözüm:
T1 tranzistoru baz bölücülü bir kuvvetlendiricidir. Bu kuvvetlendiricinin kolektör akımı için
V BB −V BE 1
1,644 − 0,6
= hFE 1
= 250
= 0,984mA re 1 = 25,41Ω
RB + (hFE 1 + 1)R 4
14,25 + 251.1
bulunur. T2 tranzistorunun kolektör akımı,
V − R 3I C 1 − V BE 1
I C 2 = hFE 2 CC
= 2,08mA
R 3 + (hFE 2 + 1)R 5
re 2 = 12Ω
olur.
b) Kaskat kuvvetlendirici, ortak emetörlü bir kuvvetlendirici ile emetör çıkışlı bir kattan
oluşmaktadır. T2’den oluşan emetör çıkışlı devrenin gerilim kazancı ve giriş direnci,
Re 2
R5
3000
Kv 2 =
=
=
= 0,996 ri 2 = hfe 2 (re 2 + R5 ) = 753kΩ
re 2 + Re 2 re 2 + R5 12 + 3000
olur. T1’den oluşan ortak emetörlü devrenin gerilim kazancı ve bazdan görülen direnç,
R // r
8112
Kv1 = − 3 i 2 = −
= −7,91 ri ′1 = hfe 1 (re 1 + R 4 ) = 256,1kΩ
re 1 + R 4
1025,41
dir. Kuvvetlendiricinin giriş direnci RB ile r′i1 dirençlerinin paralel eşdeğeridir. Buna göre,
ri = 14 ,24 // 256 ,1 = 13,5kΩ
olur. Devrenin çıkış direnci emetör çıkışlı devrenin çıkış direncidir. Bu direnç hesaplanırsa,
6
ro = (re 2 +
R3
) // R 5 = 44,8 // 3000 = 44,14Ω
hfe 2
elde edilir.
Soru 6.- Şekil 6. de kullanılan tranzistorlar için hfe=hFE=300, hre≅0, hoe≅0, |VBE|=0,6V ve
VT=25mV değerleri verilmiştir.
a) Tranzistorların çalışma noktası kolektör akımlarını hesaplayınız.
b) Vo/Vi gerilim kazancını, ri giriş direncini ve ro çıkış direncini hesaplayınız.
+15V
R7
R2
15k
13k
+
C1
T1
Vi
ri
C3
+
Vo
T4
T2
Ry
50kΩ
T3
R1
R8
300Ω
47k
R5
47k
R3
12k
C2
R4
R6
5k6
12k
R9
4k7
C4
-15V
Şekil 6.
Çözüm:
T1 ve T2 tranzistorları eştir ve baz çevrimlerindeki dirençler de doğru bileşenler açısından
eşittir. Bu durumda kolektör akımları eşit olacaktır. Kolektör akımları için
VCC + V BE 1
15 − 0,6
I C 1 = I C 2 = −hFE 1
= −300
= −0,549mA
R1 + 2(hFE 1 + 1)R 2
47 + 2.301.13
olur. re1 = re2 = 45,54Ω dir. T2 tranzistorunun kolektör akımı için baz çevriminden hareketle, T4
tranzistorunun baz akımı ihmal edilerek,
R 4 I C 2 +VBE 3
I C 3 = −hFE 3
= 1,06mA
re 3 = 23,6Ω
R 4 + (hFE 3 + 1)R 6
değeri elde edilir. T4 tranzistorunun kolektör akımı,
R 6I C 3 +VBE 4
I C 4 = −hFE 4
= 1,06mA
R 6 + (hFE 4 + 1)(R 8 + R 9 )
re 4 = 23,6Ω
ile hesaplanır.
b) Kaskat kuvvetlendiricinin gerilim kazancı katların kazançlarının çarpımına eşittir. T4 den
oluşan ortak emetörlü devrenin gerilim kazancı
R y′ 4
R 7 // R y
11538
Kv 4 = −
=−
=−
= −36,7
23,6 + 300
re 4 + R e 4
re 4 + R 8
olacaktır. Bu kuvvetlendiricinin bazından görülen direnç, T3’den oluşan emetör çıkışlı devrenin
yüküdür. Bu yük,
R e 3 = R 6 // ri ′4 = R 6 // hfe 4 (re 4 + R 8 ) = 5,6 // 97 ,08 ≅ 5,3kΩ
olur. T3’den oluşan emetör çıkışlı devrenin gerilim kazancı,
7
Kv 3 =
Re 3
5300
=
= 0,996
re 3 + Re 3 23,6 + 5300
ri 3 = hfe 3 (re 3 + Re 3 ) = 1597kΩ
dır. Uzun kuyruklu devre olan giriş katının gerilim kazancı,
R // r
11911
Kv 2 = 4 i 3 =
= 130,8
2re 2
2.45,54
olur. Kaskat devrenin gerilim kazancı, katların gerilim kazançlarının çarpımına eşittir. Bu işlem
yapıldığında,
K v = K v 2K v 3K v 4 = 130 ,8.0,996.(36 ,7) ≅ 4791
biçiminde elde edilir.
Kuvvetlendiricinin giriş direnci, T1 tranzistorunun bazından görülen dirençle R1 direncinin
paralel eşdeğerine eşittir. T1’in bazından görülen direnç,
ri ′1 = 2hfe 1re 1 = 27 ,3Ω
dur. Kuvvetlendiricinin giriş direnci,
ri = R1//r′i1 = 17,3kΩ ri = R1 // ri′1 = 17,3kΩ
olur. Kuvvetlendiricinin çıkış direnci R7 direncine eşittir ve ro = 15kΩ dır.
Soru7.- Şekil 7. deki devrede kullanılan İşlemsel Kuvvetlendiriciler ideal alınabilmektedir.
a) Vo gerilimini V1 ve V2 cinsinden veren ifadeyi çıkartınız.
b) R6 = R7, R4 = R5 /2, R1 = R2 = R3 /2 ise Vo gerilimini veren ifade ne olacaktır?
c) (b) de verilen direnç eşitlikleri için Vo =0V olması istendiğine göre V1 ve V2 gerilimleri
arasında ne gibi bir ilişki olmalıdır?
Çözüm:
a) A1 işlemsel kuvvetlendiricisinin çıkış gerilimi,
Vo′ = −(
R3
R
V1 + 3 V 2 )
R1
R2
dir. A2 işlemsel kuvvetlendiricisinin çıkış gerilimi,
Vo = −
R5
R + R 4 R7
R
R + R 4 R7 R3
V1 + 5
Vo′ = −[ 5 + 5
V
R4
R 4 R6 + R7
R4
R 4 R 6 + R 7 R1 1
R + R 4 R7 R3
V
− 5
R 4 R6 + R7 R2 2
dir.
V
1
V2
R
R5
R4
R1
R
2
A
+
1
3
A2
Vo
Şekil 7.
b) R6 = R7, R4 = R5 /2 ve R1 = R2 = R3 /2 ise,
Vo = –5V1 – 3V2 = 0 ise,
V1 = –0,6V2 olmalıdır.
R6
+
R7
Vo
8
Soru 8.- Şekil 8. de kullanılan işlemsel kuvvetlendirici idealdir.
a) Vo gerilimini dirençler ve gerilimler cinsinden hesaplayınız.
b) V1=V2=V3 iken Vo=0 olması için R2 / R1 oranı ne olmalıdır.
V1
R
V2
R
V3
R1
2R
Vo
+
R2
Şekil 8.
Çözüm:
a) Vo çıkış gerilimi,
Vo = −2V1 − 2V 2 + 5
R2
V3
R1 + R 2
dir.
b) V1 = V2 = V3 alındığında Vo = 0 olması için ifadeden kolayca görüleceği gibi R2 = 4R1
olmalıdır.
Soru 9,Şekil 9. de görülen işlemsel kuvvetlendirici ideal olduğuna göre Vo /Vi gerilim kazancını
hesaplayınız.
Çözüm:
R
10R
R
0,1R
Vi
0,1R
+
V
o
Şekil 9.
−
Vi
0,1R
=
1
Vo Vo
V
V
13Vo
+
= o + o =
0,1
10R 11
R+
R 10R 12R 12R
1,1
Vo
= −54 ,54
Vi
olarak elde edilir.
Soru 10.- Şekil 10. deki devrede kullanılan işlemsel kuvvetlendiriciler idealdir.
a) Vo gerilimini V1 ve V2 gerilimleri cinsinden veren genel ifadeyi bulunuz.
9
b) V1 ve V2 gerilimleri sabit değerler alındığında, t=0 anında Vo=0, R1=R2, R3=R4 ve
R5=R6=R ise Vo geriliminin ifadesi ne olur? (RC=1 alınacaktır.)
c) (b) de verilen durum için R6=2R5 olması halinde Vo=0 değerini alması için V1 ile V2
arasında nasıl bir ilişki olmalıdır?
Çözüm:
R6
R1
R2
-
V1
A
R3
1
+
V2
C
Vo
R
5
A
2
+
R4
Vo
Şekil 10.
a) Devrede kullanılan A1 devresinden oluşan devre fark kuvvetlendiricisidir. Bu devrenin
çıkış gerilimi,
Vo′ = −
R2
R + R2 R4
V1 + 1
V
R1
R1 R 3 + R 4 2
dir. A2 devresi hem toplama işlemi yapmakta hem de entegral almaktadır. Buna göre A2 devresinin
çıkış gerilimi,
1
1
Vo = −
V1dt −
Vo′dt
R 6C
∫
R 5C
∫
ifadesi ile V1 ve V′o gerilimlerine bağlıdır. V′o geriliminin V1 ve V2 cinsinden değerinin yerine
konulması halinde Vo gerilimi, gerekli düzenlemeler yapılarak
Vo =
R 2R 6 − R1R 5
(R1 + R 2 )R 4
V1dt −
V dt
∫
R1R 5R 6
R1R 5 (R 3 + R 4 ) ∫ 2
biçiminde elde edilir.
b) Kolayca Vo’nun ifadesinden görüldüğü gibi çıkış gerilimi sadece V2 gerilimine bağlı
olmaktadır ve
Vo = − ∫V 2dt
dir. V2=st olduğuna göre entegral alındığında
V o = −V 2t
olacaktır.
c) R6 = R5 alındığında Vo = 0 kolayca göstermek mümkündür ki
V1 = 2V 2
olmalıdır.
Soru 11.- Şekil 11. de kullanılan işlemsel kuvvetlendirici ideal olduğuna göre Vo/Vi gerilim
kazancını hesaplayınız.
Çözüm:
Şekil 5. de verilen devreden Thévenin eşdeğeri alınarak gerekli hesaplar yapılırsa,
10
Vi
V
=− o
10R
20R
Vi
20R
-
4R
1,2R
R
Vo
+
Şekil 11.
bulunur ve buradan gerekli düzenlemeler yapıldığında
Vo
= −2
Vi
olarak elde edilir.
Soru 12.- Şekil 12. de kullanılan işlemsel kuvvetlendirici ideal olarak kabul edilebilmektedir.
V1=5V olduğuna göre Vo =0V olması için V2’nin alması gereken değerini hesaplayınız.
Çözüm:
İşlemsel kuvvetlendirici reel olduğundan Vo gerilimi,
V o = 2V − V1
ifadesi ile V ve V1 gerilimlerine bağlıdır. V gerilimi V2 gerilimi cinsinden hesaplanabilir. Bu hesaplar
yapıldığında,
R
V
V
-
1
2R
R
V
+
2
2R
R
V
o
2R
Şekil 12.
1
4
dir. Buna göre çıkış gerilimi Vo,
1
Vo = V 2 −V1
2
olacaktır.
Soru 13.- Şekil 13. de kullanılan işlemsel kuvvetlendiric
i idealdir. Vo gerilimini V1, V2 ve V3 gerilimleri cinsinden hesaplayınız.
Çözüm:
Şekil 13. de görülen V gerilimi, V2 ve V3 gerilimi cinsinden hesaplanırsa,
V +V
V = 2 3
2
dir. Vo gerilimi, V1 ve V cinsinden hesaplandığında,
V o = 2V − V1
V = V2
11
olacağını göstermek oldukça kolaydır. V geriliminin V2 ve V3 cinsinden ifadesi yerine konursa,
R
V1
V2
V3
R
-
R
Vo
+
R V
Şekil 13.
V o = V 2 + V 3 − V1
olacaktır.
Soru 14.- Şekil 14. de kullanılan eşlenik tranzistorlar için VCEsat=1V, Rthjc=5°C/W,
Rthch=1°C/W ve Tjmax=150˚C değerleri verilmiştir. Tranzistorlar ayrı ayrı soğutuculara bağlanmıştır.
a) Yüke aktarılabilecek maksimum güç ne kadardır? Bu sırada verimin değeri ne olur?
b) Her bir tranzistor için kullanılması gereken soğutucu yüzeylerin ısıl direnci en fazla ne
kadar olmalıdır? Ta=50°C alınacaktır.
+V CC
40V
T1
C
T2
Ry
4Ω
Şekil 14.
Çözüm:
a) Tek kaynakla beslenen B sınıfı push-pull kuvvetlendiricide yüke aktarılan maksimum güç
ve verim,
VCC
Py max =
(
2
−VCEsat )2
2R y
= 45,125W
ηmax
VCC
π 2 −VCEsat
=
= %74 ,6
2
2
olarak bulunur.
b) Her bir tranzistorda harcanan güç,
2
Ptot = 2 Py max i
π
dir. Tranzistorlar ideal alındığında yüke aktarılan maksimum güç,
Py max i =
Ptot =
2
π2
VCC2
= 50W tır. Buna göre her bir tranzistorda harcanan güç,
8R y
Py max i = 10,13W
olarak elde edilir. Her bir tranzistor ayrı soğutuculara bağlandığına göre bir tranzistor için,
12
T j max − T a = Ptot (Rthjc + Rthch + Rthha ) ifadesi yazılabilir ve bu bağıntıda değerler yerine
konduğunda soğutucunun ısıl direnci için Rthha = 3,9˚C/W değeri elde edilir.
Soru 15.- Şekil 15. de verilen devrede kullanılan eşlenik tranzistorların her biri için
Tjmax=150°C, Rthjc=2,5°C/W, Rthch=1°C/W ve Rthha=6,5°C/W değerleri verilmiştir. Bu tranzistorlar
için ICM=5A ve VCM=50V olduğuna göre, ortam sıcaklığını Ta=50°C ve VCEsat=1V alarak, yüke
maksimum güç aktaracak VCC geriliminin değeri ne kadar olmalıdır? Seçilen VCC gerilimi için yüke en
fazla ne kadar güç aktarılabilir? Bu sırada verimin değeri ne kadardır?
Çözüm:
Her bir tranzistorda harcanabilecek güç, ısıl direncin bulunuş ifadesinden yararlanılarak
hesaplanırsa,
Ptot =
T j max − T a
100
=
= 10W
Rthjc + Rthch + Rthha 2,5 + 1 + 6,5
olarak elde edilir. Bu değer tranzistorda harcanabilecek maksimum güçtür. Bu güç değeri ile Pymaxi
arasındaki ilişki karşılaştırılırsa,
+V CC
T1
T2
Ry
4Ω
-V CC
Şekil 15.
Ptot =
2
π
P
=
2 y max i
2 VCC2
→ VCC = π Ptot R y = 19,87W
π 2 2R y
olur. Akım sınırından hareketle VCC=RyICM+VCEsat=21 olarak elde edilir. Gerilim sınırından
yararlanıldığında VCC≅VCEM/2=25V olacaktır. Bu üç besleme geriliminden görüleceği gibi çözüm, üç
değer arasında en küçük olan VCC=19,87V tur. VCC=19,87V alındığında yüke aktarılabilen
maksimum güç ve verim için,
Py max =
(VCC −VCEsat )2
= 44,51W
2R y
ηmax =
π VCC −VCEsat
= %74,6
4
VCC
değerleri elde edilir.
Soru 16.a) Şekil 16. de B-Sınıfı güç kuvvetlendiricisi çıkışında maksimum Py=10W lık bir güç elde
edilebildiği ölçülmektedir. Maksimum güçte çıkış tranzistorları (T1 ve T2) üzerinde kalan gerilimin
değerini hesaplayınız.
b) T1 ve T2’nin dayanması gereken maksimum kolektör-emetör gerilimi VCEM ile maksimum
kolektör akımı ICM değerlerine olmalıdır?
c) hFE1min=hFE2min=25 olduğu dikkate alınırsa Iomin ne olmalıdır? Bu durumda T3 üzerinde
harcanan gücü hesaplayınız. VBE1=|VBE2|≅0,7V alınacaktır.
d) VBE1=|VBE2| ≈VBE4 alarak RA ve RB arasındaki ilişkiyi belirleyeniz.
13
+VCC=24V
.....
T3
T1 C
RA
T4
RB
T2
Ry
5Ω
Io
Şekil 16.
Çözüm:
a) Tek kaynakla beslenen B-sınıfı push-pull kuvvetlendiricide yüke aktarılabilen maksimum
güç,
VCC
Py max =
(
2
−VCEsat ) 2
2R y
=
(12 −VCEsat ) 2
= 10W
10
tır. Bu bağıntıdan yararlanılarak VCEsat gerilimi hesaplandığında, VCEsat=2V olur.
b) Tranzistorlar ideal alındığında yüke aktarılabilecek maksimum güç,
Py max i =
VCC2
= 14,4W tır. Bu güç değeri ile Ptot arasındaki ilişki kullanılarak, her bir
8R y
tranzistorda harcanabilecek maksimum güç için
2
Ptot = 2 Py max i = 2,92W
π
değeri elde edilir. tranzistorlardan akabilecek maksimum akım, yüke maksimum güç aktarıldığında
oluşur. Bu akım,
VCC
I CM = I y max = 2
−VCEsat
Ry
= 2A
dir. Push-pull kuvvetlendiriciyi oluşturan tranzistorların uçlarına gelen gerilim, diğer tranzistor
doymaya girdiğinde oluşacaktır. Buna göre T1 ve T2 tranzistorlarının uçları arasına gelebilecek
maksimum gerilim değeri,
VCEM ≅ VCC −VCEsat = 24 − 2 = 20V
olur.
c) Tranzistorların akım kazançlarının minimum değerleri 25 olarak verilmiştir. T1 ve T2
tranzistorlarının baz akımları, yük akımı maksimum olduğunda en büyük değerini alır. Bu akım
hesaplandığında,
I B 1 max = I B 2 max =
I y max
2000
=
= 80mA
hFE min
25
çıkar. Io akımı en az 80mA seçilmelidir. Tranzistorların baz-emetör arası 0,7V alındığında T3
tranzistorunda harcanan güç,
14
V
Ptot 3 = ( CC − VCEsat )I o = 0,904W
2
olarak hesaplanır. Bu güç değeri T3 tranzistorunda harcanabilecek maksimum güç değeridir.
d) Gerilim çoğaltıcı devreden kolayca görüleceği gibi, T1 ve T2 tranzistorlarının bazları
arasında oluşacak gerilimin 2VBE1 olabilmesi RA ve RB dirençlerinin birbirine eşit seçilmesi halinde
mümkün olacaktır.
Soru 17.- Şekil 17. de görülen işlemsel kuvvetlendirici idealdir.
a) Vo /Vg gerilim kazancını orta frekans bölgesinde hesaplayınız.
b) Devrenin alt kesim frekansı f1=20Hz ve asimptot eğiminin 40 dB/dekat olması
istenmektedir. Belirtilen özelliği sağlayacak C1 ve C2 kondansatör değerlerini hesaplayınız.
c) Devrenin üst kesim frekansını hesaplayınız.
Vi
+
Vo R 4
Vo
C1
Rg
5k
-
5kΩ
+
C2
100pF
R1
50k
Vg
R3
R2
20k
R5
20k
C
1k
Şekil 17.
Çözüm:
a) İşlemsel kuvvetlendirici ideal alındığına göre V′o/Vi gerilim kazancı, R3 ve R2 dirençleri
tarafından belirlenir ve
Vo′ R 2 + R 3
=
= 21
Vi
R2
değerine eşittir. Devrenin giriş direnci R1 = 50kΩ değerine eşittir. Bu değer kullanılarak,
Vo V i Vo′ Vo
50 21 20
R1 R 2 + R 3 R y
=
=
=
= 15,3
′
V g V g V i Vo R1 + R g R 2 R 4 + R y 55 1 25
bulunur. İşlem sırasında işlemsel kuvvetlendirici ideal olduğundan çıkış direnci sıfır alınmıştır.
b) Devrenin alt kesim frekansının 20Hz ve asimptot eğiminin de 40dB/dekat olması
istendiğine göre çakışık kutup vardır. Buna göre kutup frekansları,
f k = f 1 21 2 − 1 = 12,87Hz
olacaktır. C1 ve C2 kondansatörlerinin oluşturdukları kutup
frekansları bu değere eşit alınarak değerleri hesaplanırsa,
1
1
C1 =
= 0,225 µF
C2 =
= 0,495 µF
2πf k (R g + R1 )
2πf k (R 4 + R y )
değerleri elde edilir.
c) Devrenin üst kesim frekansı C kondansatörü ile belirlenmektedir. Bu kondansatörün
uçları arasına gelen eşdeğer direnç, R4 ve Ry dirençlerinin paralel eşdeğeridir. Bu direnç
hesaplanırsa, R = R4// Ry = 4kΩ olarak bulunur. Buna göre devrenin üst kesim frekansı,
1
1
f2 =
=
≅ 398kHz
2πCR 2π 100.10 −12 4.10 3
bulunur.
15
Soru 18.- Şekil 18. deki blok şemada kullanılan kuvvetlendirici blokların yüksüz
büyüklükleri:
K1=50 ri1=50kΩ
Ci1=50pF
ro1=5kΩ
Co1=5pF
K2=20 ri2=100kΩ
Ci2=20pF
ro2=1kΩ
Co2=2pF
olarak verilmiştir. Rg=10kΩ ve Ry=20kΩ dur.
a) Devrenin Vo/Vg gerilim kazancını orta frekans bölgesi için hesaplayınız.
b) Vo/Vg kazancının alt kesim frekansının f1=20Hz ve asimptot azalma eğiminin 40dB/dekat
olması istendiğine göre C1 ve C2 kondansatörlerinin değerini hesaplayınız.
c) Yüksek frekans bölgesi kutup frekanslarını hesaplayınız.
C
Rg
+
10kΩ
Vg
C 2 Vo
1
r i1
C i1
K
1
r o1
r i2
C o1
C i2
K
Ry
2
ro2 20kΩ
C o2
Şekil 18.
Çözüm:
a) Devrenin orta frekans bölgesinde Vo/Vg gerilim oranı
Ry
Vo
50 100 20
ri 1
ri 2
= K 1K 2
= 50.20
= 755,86
60 105 21
Vg
ri 1 + R g ro 1 + ri 2 ro 2 + R y
olarak hesaplanır.
b) Devrenin alt kesim frekansının 20Hz ve asimptot eğiminin de 40dB/dekat olması
istenmektedir. Çakışık kutup durumu olduğundan önceki soruda olduğu gibi kutup frekansları için,
fk1 = fk2 = 12,87Hz değerleri elde edilir. Bu değerler ve C1 ile C2 kondansatörlerinin çevrimine giren
dirençler kullanılarak
1
1
C1 =
= 0,206 µF
C2 =
= 0,589µF
2πf k (R g + r i 1 )
2πf k (ro 2 + R y )
değerlerine varılır.
c) Yüksek frekans bölgesinde 3 tane kutup oluşacaktır. Bu kutuplara karşılık gelen kutup
frekansları,
1
1
fk1 =
=
≅ 191kHz
2πC i 1 (R g // ri 1 ) 2π 50.10 −12 8333
1
1
=
= 1,34MHz
2π (C o 1 + C i 2 )(ro 1 // ri 2 ) 2π 25.10 −12 4762
1
1
=
=
= 83,6MHz
2πC o 2 (ro 2 // R y ) 2π 2.10 −12 952,4
fk 2 =
fk 3
biçiminde hesaplanırlar.
Soru 19.- Şekil 19. de kullanılan kuvvetlendiricinin girişine orta frekans bölgesinde
Vg=10mV’luk bir gerilim uygulandığında kuvvetlendiricinin çıkışında 2V gerilim ölçülmektedir.
Devrenin alt kesim frekansı f1=40Hz ve asimptot eğimi 40dB/dekat tır. Devrenin üst kesim frekansı
f2=1MHz olarak ölçülmüştür. Çıkış kapasitesi Co ihmal edilecek kadar küçüktür.
a) Devrenin giriş ve çıkış direncini hesaplayınız.
16
b) Devrenin yüksüz gerilim kazancı K ne kadardır?
c) Devrenin giriş kapasitesini hesaplayınız.
Çözüm:
a) Devrenin alt kesim frekansı f1= 40Hz olarak ölçülmüş ve asimptot eğiminin 40dB/dekat
olduğu görüldüğüne göre çakışık kutup vardır. Bu kutup frekansı hesaplanırsa,
f k = f 1 21 2 − 1 = 25,74Hz
olarak elde edilir. C1 ve C2 kondansatörlerinin oluşturacakları kutup frekansları bu değere eşit
olmalıdır. devreden hareketle bu frekanslar yazılırsa,
C
1
100nF
+
R
10kΩ
+
Vg
ri
Ci
350nF
C2
Vo
K
-
ro
+
Ry
10kΩ
Şekil 19.
fk1 =
1
2πC 1 (R g + ri )
fk 2 =
1
2πC 2 (ro + R y )
dir. Bu bağıntılardan yararlanılarak ri ve ro dirençleri hesaplanırsa,
1
ri =
− R g = 51830Ω
2πC 1f k 1
ro =
1
2πC 2f k 2
− R y = 7666Ω
bulunurlar.
b) Devrenin Vo/Vg oranı verilen değerlerden hareketle hesaplanırsa,
Vo 2000
=
= 200
10
Vg
dir. Devreden kolayca görüldüğü gibi bu kazanç,
Ry
Vo
51830 10000
ri
=K
=K
= 200
Vg
r i + R g ro + R y
61830 17666
dir. Bu ilişkiden hareketle K için 421,5 değeri elde edilir.
c) Devrenin üst kesim frekansı Ci kapasitesinden oluşmaktadır. Bu kapasiteye paralel gelen
eşdeğer direnç, Rg ve ri dirençlerinin paralel eşdeğeridir. Bilinen değerler kullanıldığında bu direnç
için R=Rg//ri =8,38kΩ değeri bulunur. Üst kesim frekansı 1MHz olarak verilmiştir. Üst kesim
frekansı tek kutupla belirlendiğinden Ci kapasitesi,
1
1
Ci =
=
≅ 19pF
2πf 2R 2π 1.10 6 8380
bulunur.
Soru 20.- Şekil20. deki devrede kullanılan kuvvetlendiricinin yüksüz gerilim kazancı
K=2000, giriş direnci r′i=50kΩ ve çıkış direnci r′o=500Ω dur.
a) Devrenin Vo/Vg gerilim kazancını hesaplayınız.
b) Devrenin alt kesim frekansının 20Hz ve asimptot eğiminin 40dB/dekat olması istendiğine
göre C1 ve C2 kondansatörlerinin değerini hesaplayınız.
17
c) Devrenin üst kesim frekansını hesaplayınız.
Çözüm:
a) Devrede seri gerilim geribeslemesi bulunmaktadır. β devresi, R2 ve R3 dirençlerinden
oluşur. Bu devreden β fonksiyonu hesaplanırsa,
R2
1,5
1
β =−
=−
=−
R2 + R3
30 + 1,5
21
olarak elde edilir. β devresinin girişinden ve çıkışından görülen dirençler hesaplandığında
+
Rg
C
10k
+
Vg
1
Vo
K
ri
R1
-
100k
R2
30k
ro
5k
C2
+
Vo
R4
R3
C
50pF
Ry
20kΩ
1k5
Şekil 20.
r iβ = R 2 + R 3 = 31,5kΩ
roβ = R 2 // R 3 = 1,43kΩ
olarak bulunurlar. Bu dirençlerin devreye dahil edilmesi ile devrenin açık çevrim büyüklükleri
hesaplanırsa,
ri = ri ′ + roβ = 50 + 1,43 = 51,43kΩ
ro = ro′ // riβ = 492,2Ω
değerleri elde edilir. Devrenin açık çevrim kazanç fonksiyonu,
V′
r ′ R y′
Kv = o = K i
Vt
ri ro′ + R y′
biçimindedir. Bağıntıda görülen R′y=riβ//(R4+Ry)=13,94kΩ dır. Bu direnç bağıntıda kullanıldığında Kv
kazancı için
50
13,94
K v = 2000
= 1877
51,43 13,94 + 0,5
değerine varılır. Devrenin geribeslemeli gerilim kazancı Kvf, V′o ile Vi arasında tanımlanmıştır. Bu
kazanç hesaplanırsa,
V′
Kv
K vf = o =
= 20,77
V i 1 − βK v
olur. Vo/Vg kazancı istenmektedir. Bu kazancın hesaplanabilmesi için geribeslemeli giriş direnci rif
hesaplanmalıdır. rif giriş direnci, r′if ile R1 dirençlerinin paralel eşdeğeridir. r′if direnci hesaplanırsa,
1877
rif′ = ri (1 − βK v ) = 51,43(1 +
) = 4648,3kΩ
21
olarak bulunur. Bu direnç değerinin kullanılması ile
r if = R1 // r if′ = 100 // 4648 ,3 = 97 ,9kΩ
biçiminde geribeslemeli rif direnci elde edilir. Bu direnç kullanılarak devrenin Vo/Vg gerilim oranı,
Ry
Vo V i Vo′ Vo
97,9
20
rif
=
=
=
20,77
= 15,08
K vf
20 + 5
V g V g V i Vo′ R g + rif
R 4 + R y 97,9 + 10
olur.
18
b) Devrenin alt kesim frekansının 20Hz olması istenmektedir. Asimptot eğiminin 40dB/dekat
olması istendiğinden çakışık kutup durumu vardır. Çakışık kutup frekansı,
f k = f 1 21 2 − 1 = 12,87Hz
olur. C1 ve C2 kondansatörlerinin değerinin hesaplanabilmesi için rof direncinin değerinin
hesaplanması gerekir. Bu direncin değerinin bulunabilmesi için K′v kazancı hesaplanabilmelidir.
Devreden hareketle
K v′ = K
50
31,5
r i ′ r iβ
= 2000
= 1914
′
51,43 31,5 + 0,5
r i r o + r iβ
biçiminde K′v kazancı hesaplanır. rof geribeslemeli çıkış direnci,
rof =
ro
1 − β K v′
=
ri
ri + R g′
ro
ri
1− βK′
ri + (R g // R1 )
= 6,27Ω
olarak hesaplanır. C1 ve C2 kondansatörlerinin çevrimindeki dirençler ve oluşan kutup frekansları
bilindiğinden bu iki kondansatörün değeri için
1
1
C1 =
=
= 0,115 µF
2πf k (R g + rif ) 2π 12,87(10.10 3 + 97,9.10 3 )
C2 =
2πf k (rof
1
1
=
= 0,495 µF
+ R 4 + R y ) 2π 12,87(6,27 + 5.10 3 + 20.10 3 )
bulunur.
c) Devrenin üst kesim frekansı C kondansatörü ve bu kondansatörün uçları arasına gelen eş
değer dirençle belirlenmektedir. Buna göre,
1
1
f2 = fk =
=
= 795kHz
−12
2πC [(rof + R 4 ) // R y ] 2π 50.10 (5006,27 // 20.10 3 )
üst kesim frekansı elde edilir.
Soru 21.- Şekil 21. deki devrede kullanılan kuvvetlendiricinin giriş direnci çok büyük, çıkış
direnci ise çok küçüktür. Kuvvetlendiricinin kazanç fonksiyonu
C
Rg
10kΩ
+
Vg
1
Vi
+
Vo
K(s)
100k
R1
C2
Vo
R6
-
20k
R2
2k
10k
R3
R4
R5
Ry
20kΩ
1k
5k
Şekil 21.
K (s ) =
2π 10 8
s + 2π 105
biçiminde verilmiştir.
a) Orta frekans bölgesinde Vo /Vg =Kvko değerini hesaplayınız.
b) Devrenin alt kesim frekansı 20Hz ve asimptotun azalma eğiminin 40db/dekat olabilmesi
için C1 ve C2 kondansatörlerinin değerini hesaplayınız.
19
c) Devrenin üst kesim frekansını hesaplayınız.
Çözüm:
a) Kuvvetlendiricinin kazanç fonksiyonu yüksek frekans bölgesine ait bir fonksiyondur. Bu
fonksiyon biçiminden yararlanılarak kuvvetlendiricinin orta frekans bölgesi kazancı hesaplanabilir.
Yüksek frekans bölgesinde bir kutbu bulunan kazanç fonksiyonu,
K v (s ) =
K vo ωk
s + ωk
biçimindedir. Bu fonksiyonla verilen kazanç fonksiyonunun karşılaştırılması ile Kvo = 1000 olarak
bulunur. Devreye seri gerilim geribeslemesi uygulanmıştır. β devresi, R2, R3, R4 ve R5 dirençlerinden
oluşmaktadır. Kuvvetlendiricinin giriş direnci çok büyük, çıkış direnci de çok küçük verildiğinden, β
devresinin yükleme etkisi olmayacaktır. Dört dirençten oluşan β devresinin gerilim oranı, Thévenin
dönüşümü ile kolayca
V
R 2R 4
1
β = f =−
=−
Vo′
(R 4 + R 5 )(R 2 + R 3 ) + R 4R5
57
biçiminde elde edilir. R6 direnci çevrim dışında kalmakta ve geribeslemeli devrenin çıkışına seri
gelmektedir. Orta frekans bölgesi Vo/Vg gerilim oranı,
Vo V i Vo′ Vo
=
V g V g V i Vo′
ifadesi ile hesaplanabilir. Bu ifadede görülen oranların bağıntıları kullanıldığında Vo/Vg gerilim oranı,
Ry
Vo
K vo
rif
=
V g R g + rif 1 − βK vo R 6 + R y
olur. rif geribeslemeli giriş direnci, açık çevrim giriş direnci çok büyük olduğundanR1= 100kΩ
değerine eşittir. Bilinen büyüklüklerin kullanılması ile
V
20
100
1000
K vko = o =
= 44 ,6
V g 100 + 10 1 + 1000 2 + 20
57
olarak bulunur.
b) Alt kesim frekansının 20Hz ve asimptot eğiminin 40dB/dekat olması istendiğine göre
çakışık kutup vardır. Buna göre kutup frekansları,
f k = f 1 21 2 − 1 = 12,87Hz
olur. Bu kutup frekanstan yararlanılarak
1
C1 =
= 0,112 µF
2πf k (R g + R1 )
C2 =
1
2πf k (R 6 + R y )
= 0,562 µF
kondansatör değerleri bulunur.
c) Üst kesim frekansı, kuvvetlendiricinin açık çevrim kazanç fonksiyonundan
kaynaklanmaktadır. Açık çevrim kazanç fonksiyonunda tek kutup bulunan bir kuvvetlendiriciye
frekanstan bağımsız geribesleme uygulandığında üst kesim frekansı (1–βKv) kadar artar. Açık
çevrim üst kesim frekansı, f2=100kHz dir. Buna göre geribeslemeli üst kesim frekansı,
1000
f 2f = (1 − βK v )f 2 = (1 +
)100 = 1854,4kHz = 1,854MHz
57
olur.
Soru 22.- Şekil 22. de kullanılan kuvvetlendiricinin yüksüz gerilim kazancı K=500, giriş
direnci r′i=50kΩ, çıkış direnci r′o=500Ω olarak verilmiştir. R1=5kΩ, R2=200kΩ, Ry=20kΩ, C1=1µF ve
C2=250nF tır.
20
a) Devrenin Vo/Vi gerilim kazancını hesaplayınız.
b) Devrenin alt kesim frekansını hesaplayınız.
Çözüm:
a) Devreye R2 direnci üzerinden paralel gerilim geribeslemesi uygulanmıştır. β devresi R2
direncinden oluşmaktadır. Geribesleme devresi β’nın giriş ve çıkış dirençleri,
riβ = R 2 = 200kΩ
roβ = R 2 = 200kΩ
dır. β devresinin yükleme etkisi ile kuvvetlendiricinin açık çevrim büyüklükleri,
r i = R 2 // r i ′ = 50 // 200 = 40kΩ
ro = ro′ // R 2 = 500 // 200k = 499Ω
direnç değerleri bulunur. Kuvvetlendiricinin açık çevrim gerilim kazancı,
K v = −K
R 2 // R y
200 // 20
18,2
= −500
= −500
= −486,6
ro′ + (R 2 // R y )
0,5 + (200 // 20)
0,5 + 18,2
olur. Paralel gerilim geribeslemesinde kuvvetlendiricinin gerilim kazancı geribesleme ile değişmez.
Buna göre Vo/Vi gerilim kazancı,
+
C1
R1
R2
-
Vi
C2
K
ri
+
ro
+
Vo
Ry
Şekil 22.
Vo
rif
= Kv
Vi
rif + R1
olacaktır. rif direncinin bulunması gerekmektedir. Bunun için açık çevrim geçiş empedansı
hesaplanmalıdır. Gerilim kazancı ile geçiş empedansı arasındaki ilişkiden yararlanılarak
Z m = K v ri = −486 ,6.40kΩ = −19464 kΩ
olarak hesaplanır. β=1/R2 dir. Buna göre geribeslemeli giriş direnci,
ri
ri
40
=
=
= 406,8Ω
rif =
K v ri
1 − βZ m
98,32
1−
R2
olacaktır. Bu direncin kullanılması ile devrenin Vo/Vi gerilim kazancı,
Vo
rif
406,8
= Kv
= −486,6
= −36,6
Vi
R1 + rif
406,8 + 5000
değeri elde edilir.
b) Devrenin alt kesim frekansının hesaplanması istenmektedir. Bu frekans C1 ve C2
kondansatörleri ve çevrimine giren dirençler tarafından belirlenir. C1 kondansatörünün çevriminde
bulunan dirençlerin toplamı, R1 ve rif dirençlerinin toplamına eşittir. Buna göre C1 kondansatörünün
oluşturduğu kutup frekansı,
1
1
fk1 =
=
= 29,44Hz
−6
2πC 1 (R1 + rif ) 2π 10 (5000 + 406,8)
dir. C2 kondansatörünün çevrimine giren dirençlerin toplamı, Ry ve rof dirençlerinin toplamına eşittir.
rof direncinin hesaplanması gerekir. Geribeslemeli çıkış direnci,
21
rof =
ro
1 − βZ m′
R1
r i + R1
ifadesi ile hesaplanır. Z′m geçiş empedansı, Ry açık devre iken bulunan geçiş empedansıdır. Bu
empedans, yük açık devre iken bulunan gerilim kazancı ile giriş direncinin çarpımına eşittir. Yük
açık devre edildiğinde devrenin gerilim kazancı,
K v′ = −K
r iβ
ro′ + riβ
= −500
200
= −498,8
0,5 + 200
dir. Bu kazanç değeri kullanıldığında Z′m=-498,8.40kΩ= – 19952kΩ
olur. Z′m geçiş empedansının kullanılması ile geribeslemeli çıkış direnci,
499
rof =
= 41,3Ω
19952 5
1+
200 40 + 5
olur. C2 kondansatörünün oluşturduğu kutup frekansı,
1
fk 2 =
= 31,8Hz
2πC 2 (rof + R y )
olarak hesaplanır. Kutup frekansları eşit olmasa da birbirine çok yakındır. Bu durumda
f k = f k 1f k 2 = 30,6Hz
değerinde çakışık iki kutup varmış gibi alt kesim frekansı hesaplanır. Bu hesaplar yapılırsa,
f1 =
fk
12
2
−1
= 47,5Hz
olacaktır.
Soru 23.- Şekil 23. de görülen kuvvetlendiricinin yüksüz büyüklükleri K=1000, r′i=100kΩ,
r′o=200Ω olarak verilmiştir. R1=100KΩ, R2=1kΩ, R3=15kΩ, Rg=10kΩ ve Ry=10kΩ dır.
a) Devrenin Vo/Vi gerilim kazancını hesaplayınız.
b) Devrenin Vo/Vg gerilim kazancının ve geribeslemeli rof çıkış direncinin değerini bulunuz.
Çözüm:
a) Devre, seri gerilim geribeslemesi uygulanmış bir kuvvetlendiricidir. Kuvvetlendiricinin
geribeslemeli ifadelere diren büyüklükleri olan Kv, ri ve ro değerlerinin hesaplanması gerekir. β
devresinin giriş ve çıkışından görülen ve yükleme etkisin belirleyen dirençler,
riβ = R 2 + R 3 = 16kΩ roβ = R 2 // R 3 = 937,5Ω
dur. Bu dirençlerle birlikte kuvvetlendiricinin yükleme etkisi ile sağladığı gerilim kazancı,
Kv = K
R y // riβ
100
6
ri ′
= 1000
= 958,8
100 + 0,9375 0,2 + 6
ri ′ + roβ ro′ + (R y // riβ )
olacaktır. Geribesleme katsayısı β,
R2
1
β =−
=−
R2 + R3
16
dır. Bu Kv ve β değerleri kullanılarak geribeslemeli gerilim kazancı,
Kv
958,8
K vf =
=
= 15,74
958,8
1 − βK v
1+
16
olacaktır.
22
Vi
+
+
Rg
ri
K
-
R1
Vg
R3
+
Vo
ro
rof
R2
Ry
Şekil 23.
b) Vo/Vg gerilim kazancının hesaplanması için rif geribeslemeli giriş direncinin hesaplanması
gerekir. Geribeslemeli giriş direnci,
rif = R1 // rif′ = R1 // ri (1 − β K v ) = R1 //( ri′ + roβ )(1 − β K v ) = 98,4kΩ
dir. Bu dirençle
rif
Vo
=
K vf = 14,3
Vg Rg + rif
elde edilir. rof direncinin hesaplanması için K′v kazancı ve R1//Rg=R′g dirençlerinin hesaplanması
gerekir. K′v kazancı, yük açık devre edilerek hesaplanan gerilim kazancıdır. Bu kazanç ve direnç
hesaplanırsa,
riβ
ri′
K v′ = K
= 978,5 Rg′ = R1 // Rg = 9,09kΩ
ri′ + roβ ro′ + roβ
olurlar. Geribeslemeli çıkış direnci, açık çevrim çıkış direnci ro=r′o//riβ=197,5Ω olduğundan
ro
197,5
rof =
=
= 3,46Ω
ri
978,5 100,94
1+
1 − β K v′
16 100,94 + 9,09
ri + R′g
olur.
Soru 24. Şekil 24 deki devrede kullanılan kuvvetlendiricinin giriş direnci ri çok büyük, giriş
kapasitesi Ci çok küçük ve ro çıkış direnci ile Co çıkış kapasitesi ihmal edilecek kadar küçüktür.
Kuvvetlendiricinin kazanç fonksiyonu
K (s) = K o
ω1ω 2
( s + ω1 )(s + ω 2 )
biçiminde verilmiştir. Ko=1000 olarak verilmiştir.
a) Frekans eğrisinde tepe oluşmaması için ω2/ω1 oranı hangi koşulu sağlamalıdır?
b) Vo/Vg gerilim kazancının alt kesim frekansını hesaplayınız.
c) ξ= 1/ 2 olduğu durumda devrenin üst kesim frekansını ω1=4.103rad/s olduğuna göre
hesaplayınız.
Çözüm:
a) Frekans eğrisinde tepe oluşmama koşulu (14.34) bağıntısı ile verilmiştir. Bu bağıntıya
göre
fk 2
≥ −2 βK o
fk1
koşulunun sağlanması gerekir. Devreden görüldüğü gibi
23
β =−
R2
R2 + R3
=−
1
40
dır. Bu β değeri ve Ko değerleri kullanılarak frekans eğrisinde tepe oluşmaması için
C1
0,1µF
+
Vg
1
K(s)
Rg
10kΩ
C
+
R1
0,1µF
-
100k
R2
+
Vo
Ry
R 3 39k
10kΩ
1k
Şekil 24.
2
ω2
≥
1000 = 50
ω1 40
ω2
≥ 50
ω1
koşulunun sağlanması gerekir.
b) C1 ve C2 kondansatörleri nedeniyle alçak frekans bölgesinde oluşan kutup frekansları,
1
1
fk1 =
= 14 ,5Hz
fk 2 =
= 13,3Hz
2πC 1 (R g + R1 )
2πC 2R y
değerleri elde edilir. Kutup frekansları bir birine çok yakındır. Bu nedenle
f k = f k 1f k 2 = 13,9Hz
olur ve alt kesim frekansı için
f1 =
fk
21 2 − 1
= 21,6Hz
olacaktır.
c) Frekans eğrisinde tepe olmaması ile ξ=1/ 2 aynı duruma karşılık düşer. Frekans
eğrisinde tepe oluşmadığına göre ω2=50ω1 eşitliği sağlanıyor demektir. Frekans ξ=1/ 2
olduğunda üst kesim frekansı f2=fo dur. ω2 ve ω1’in toplamı
2ωo = (ω 2 + ω1 ) = 51ω1 = 51.4.10 3 → f 2 = f o =
2 ωo olduğundan
204000
2π 2
= 22958Hz
olur. Devrenin üst kesim frekansı f2 ≅ 22,96kHz dir.
Soru 25.- Şekil 25. deki devrede kullanılan kuvvetlendiricinin giriş direnci ri çok büyük, giriş
kapasitesi Ci çok küçük ve ro çıkış direnci ile Co çıkış kapasitesi ihmal edilecek kadar küçüktür.
Kuvvetlendiricinin kazanç fonksiyonu
K (s ) = K o
ω1ω 2
(s + ω1 )(s + ω 2 )
biçimindedir. Ko=1000 ve ω2= 100ω1= 106 rad/s olarak verilmiştir.
a) Frekans eğrisinde tepe oluşmaması için R3/R2 oranı hangi koşulu sağlamalıdır?
b) ξ=1/ 2 için devrenin üst kesim frekansını hesaplayınız.
24
c) Vo/Vg gerilim kazancının alt kesim frekansının 50Hz ve asimptot eğiminin 40dB/dekat
olması için C1 ve C2 kondansatörlerinin değerini hesaplayınız.
C1
C
+
K(s)
Rg
10kΩ
+
Vg
R1
R2
+
Vo
-
100k
1
Ry
R3
10kΩ
Şekil. 25.
Çözüm:
a) Frekans eğrisinde tepe oluşmaması, (14.34) bağıntısına karşılık gelmektedir. Bu koşula
göre
ω2
2R 2
R2
ω2
1
Ko →
≥ −2 β K o =
≤
=
ω1
R2 + R3
R 2 + R 3 2K o ω1 20
koşulunun sağlanması gerekir. Bu koşuldan hareketle
R3
≥ 19
R2
koşulu elde edilir.
b) Sönüm katsayısı ξ=1/ 2 olduğunda üst kesim frekansı f2=fo dır. Bu durumda β= –1/20
dir. Bu değer kullanıldığında
2ωo = ω 2 + ω1 = 101.10 4 rad / s → f 2 = f o =
101.10 4
2 2π
≅ 119,7kHz
olarak üst kesim frekansı bulunur.
c) Devrenin alt kesim frekansı 50Hz olsun isteniyor. Asimptot eğimi 40dB/dekat olduğundan
çakışık kutup vardır. Buna göre çakışık kutup frekansı,
f k = f 1 21 2 − 1 = 32,2Hz
olur. Bu kutup frekansının C1 ve C2 kondansatörleri tarafından sağlanması gerekir. C1 ve C2
kondansatörlerinin çevrimine giren dirençlerden hareketle
1
1
C1 =
=
≅ 45nF
2πf k (R1 + R g ) 2π 32,2.110.10 3
C2 =
1
1
=
= 0,494 µF
2πf k R y
2π 32,2.10.10 3
değerleri bulunur.
Soru 26.- Şekil 26. deki devrede kullanılan kuvvetlendiricinin kazanç fonksiyonu,
K (s ) =
K o ω1ω 2ω 3
(s + ω1 )(s + ω 2 )(s + ω 3 )
biçiminde verilmiştir. Kuvvetlendiricinin giriş direnci sonsuz sayılacak kadar büyük, çıkış direnci ise
ihmal edilecek kadar küçüktür. ω1=300 rad/s, ω2=ω3=106rad/s ve Ko=104 olarak verilmiştir.
a) Devrenin frekans eğrisinde tepe oluşmaması için R2/R1 oranının kritik değerini
hesaplayınız.
25
b) Devrenin osilasyon yapması hangi R2 / R1 oranında meydana gelir?
Vi
+
K (s)
v
R1
Vo
R2
Şekil 26.
Çözüm:
a) Üç kutuplu durumda frekans eğrisinde tepe oluşmaması için (14.44) koşulunun
sağlanması gerekir. Bu koşul,
1− β Ko ≤
[f k 3 (f k 1 + f k 2 ) + f k 1f k 2 ] 2
2f k 1f k 2f k 3 (f k 1 + f k 2 + f k 3 )
biçimindedir. Bu bağıntıda kutup frekansları kullanıldığında,
1
1 − β K o ≤ 3334,8 → − β .10 4 ≤ 3333,8 → − β ≤
3
koşuluna varılır. Devreden görüldüğü gibi
R1
R
1
−β =
≤ → 2 ≥2
R1 + R 2 3
R1
koşulunun sağlanması gerekmektedir.
b) Devrenin osilasyon yapması, Barkhausen koşulunun sağlanması demektir. Buna göre
β K ( jω ) = 1
sağlanmalıdır. K(s) kazanç fonksiyonunun payda polinomunun parentezleri açılırsa,
K (s ) =
K o ω1ω 2ω 3
s + s (ω1 + ω 2 + ω 3 ) + s (ω1ω 2 + ω 2ω 3 + ω 3ω1 ) + ω1ω 2ω 3
3
2
biçimini alır. Bu fonksiyonda s=jω konarak β ile çarpılırsa,
β K o ω1ω 2ω 3
=1
ω1ω 2ω 3 − ω (ω1 + ω 2 + ω 3 ) + jω (ω1ω 2 + ω 2ω 3 + ω 3ω1 − ω 2 )
2
olmalıdır. Eşitliği sağ tarafı reel olduğundan paydanın sanal kısmı 0’a eşit olmalıdır. Buna göre,
ω1ω 2 + ω 2ω 3 + ω 3ω1 − ω 2 = 0 → ωo2 = ω1ω 2 + ω 2ω 3 + ω 3ω1
olacaktır. Bağıntıda görülen ωo osilasyon açısal frekansıdır. Bu ifade ile bulunan ω2o, kullanılarak,
− β K o ω1ω 2ω 3 = 2ω1ω 2ω 3 + ω12 (ω 2 + ω 3 ) + ω 22 (ω1 + ω 3 ) + ω 32 (ω1 + ω 2 )
eşitliğine varılır. Açısal frekansların değerleri yerlerine konduğunda
R1
1
−β =
≅
R1 + R 2 1,5
olur. Bu ifadeden
R 2 = 0,5R1
koşulu elde edilir. Devrenin osilasyon yapması için R2=0,5R1 olmalıdır.
Soru 27.a) Şekil 27. deki devrenin girişine orta frekanslarda sinüsoidal işaret uygulandığında
Vo/Vg=50 ve Vo /Vi = 60 olmaktadır. Devrenin giriş direncini hesaplayınız.
26
b) Devrenin girişine yükselme süresi
trg=10ns
olan kare dalga uygulanmıştır. Giriş direnci
rio=10MΩ, giriş kapasitesi Cio=3.5pF ve 50MHz band genişliği olan osiloskopla devrenin girişinde
ölçülen yükselme süresi tri=0.23µsn olmaktadır. Devrenin giriş kapasitesini bulunuz.
c) Kuvvetlendiricinin çıkış direnci ro=5kΩ, çıkış kapasitesi Co=5pF ise, aynı osiloskop
kullanıldığında ölçülen yükselme süresi ne kadar olur.
d) Kare dalganın frekansı 1kHz olduğunda, C1 ve C2 kondansatörlerinin her birinin
oluşturduğu darbe üstü eğilmesinin % 0,5 olması için C1 ve C2 ne olmalıdır.
e) Devrenin alt ve üst kesim frekanslarını bulunuz.
C 1 Vi
C2
+
5kΩ
Vo
Rg
+
Vg
Ci
Co
ri
ro
Ry
10k
Şekil 27.
Çözüm:
a) Kuvvetlendiricinin Vo/Vg gerilim kazancının Vo/Vi kazancı cinsinden yazılması ile
Vo
ri V o
=
V g ri + R g V i
eşitliği elde edilir. Bu eşitlikte bilinen değerler yerine konduğunda ri=5Rg olarak bulunur. Buna göre
ri = 25kΩ olmalıdır.
b) Kuvvetlendiricinin girişine osiloskop bağlandığında ölçülen yükselme süresi, giriş
yükselme süresi trg, osiloskobun kuvvetlendiricisinden gelen yükselme süresi ve devrenin girişindeki
eşdeğer kapasiteden kaynaklanır. Buna göre
2
2
2
2
t ri = 1,1 t rg + t rio + t ros → t rio
⎛t ⎞
2
= ⎜ ri ⎟ − t rg2 − t ros
1
,
1
⎝
⎠
dir. Osiloskobun band genişliğinden hareketle oluşacak yükselme süresi için
0,35
t ros =
= 7ns
50.10 6
değeri elde edilir. Bilinen değerlerin kullanılması ile devrenin giriş eşdeğer kapasitesinden
kaynaklanan yükselme süresi,
t rio = 208 ,7ns
olarak hesaplanır. Bu yükselme süresine karşılık gelen kutup frekansı,
f ki =
0,35
1
=
= 1,677 MHz
−9
2πCeş ( Rg // ri // rio )
208,7.10
olur. Buradan eşdeğer giriş kapasitesi,
C eş = 23,73pF = C i + C io → C i = C eş − C io = 23,73 − 3,5 = 20,23pF
olarak hesaplanır.
c) Osiloskop devrenin çıkışına bağlandığında oluşacak yükselme süresi,
2
2
t roö = 1,1 t rg2 + t rio
+ t ro2 + t ros
27
olacaktır. bu bağıntıda bilinmeyen tro yükselme süresi, kuvvetlendiricinin çıkışında oluşan eşdeğer
kapasitenin belirlediği yükselme süresidir. Bu kapasitenin değeri Coeş=Co+Cio=5+3,5=8,5pF tır. Bu
eşdeğer kapasiteye paralel gelen eşdeğer direnç,
R eş = ro // R y // rio = 3332,8Ω
dur. Çıkışta oluşan kutup frekansı ve yükselme süresi,
1
0,35
f ko =
= 5,62MHz t ro =
= 62,28ns
2πC oeş Reş
5,62.10 6
olur. Bu yükselme süresi kullanılarak kuvvetlendiricinin çıkışındaki yükselme süresi,
t roö = 1,1 102 + 208,7 2 + 62,282 + 7 2 = 240ns = 0,24 µs
değerinde elde edilir.
d) Uygulanan kare dalganın frekans 1kHz verildiğinde her bir kondansatörün oluşturduğu
darbe üstü eğilmesinin δ=%0,5 olması isteniyor. C1 ve C2 kondansatörlerinden kaynaklanan darbe
üstü eğilmeleri ve kondansatör değerleri,
1
1
δ1 =
= 0,005 → C 1 =
= 3,33µF
3
2fC 1 (R g + ri )
2.10 0,005.30.10 3
δ2 =
1
1
= 0,005 → C 2 =
= 6,67 µF
3
2fC 2 (R y + ro )
2.10 0,005.15.10 3
biçiminde bulunur.
e) Devrenin alt ve üst kesim frekanslarının değerlerinin hesaplanması isteniyor. Alçak
frekans bölgesindeki kutup frekansları hesaplanmak istendiğinde eğilmeler eşit olduğundan kutup
frekansları da eşit olacaktır. Buna göre,
1
fk1 = fk 2 =
= 1,59Hz
2πC 1 (R g + ri )
olur. Devrenin alt kesim frekansı,
f1 =
fk
21 2 − 1
= 2,47Hz
olacaktır.
Yüksek frekans bölgesinde oluşan kutup frekansları,
1
1
f ki =
=
= 1,89MHz
2πC i (R g // r i ) 2π 20,23.10 −12 4167
f ko =
1
1
=
= 9,55MHz
2πC o (ro // R y ) 2π 5.10 −12 3333
olurlar. Buradan üst kesim frekansı için
1
f2
= 1,1
1
2
f ki
+
1
f ko2
→ f 2 = 1,685MHz
değeri bulunur.
Soru 28.Şekil 28. de görülen iki kapılı devrenin girişine frekansı 1kHz olan sinüsoidal işaret
uygulanınca Ry direncinin uçları arasında 1,5V’luk değişken bir gerilim ölçülmüştür. Kuvvetlendirici
A-B uçları arasına bağlı olmadığında bu uçlar arasında ölçülen gerilim 50mV’tur. Kuvvetlendirici
bağlandığında Vo=1,5V iken Vi=40mV olmaktadır. İşaret kaynağı periyodik bir darbe olduğunda
kuvvetlendirici bağlı değilken A-B uçları arasında ölçülen yükselme süresi trg=7ns dir.
28
Kuvvetlendirici A-B uçları arasına bağlanınca yükselme süresi tri=0,3µs ve çıkış yükselme süresi
tro=0,4µs olmaktadır.
A
5kΩ
+
+
Vo
V
Rg i
Ry
Vg
B
Şekil 28.
a) Devrenin giriş direnci ve kapasitesini hesaplayınız.
b) Vo/Vg’nin yüksek frekans bölgesinde iki kutbu bulunduğuna göre bu kutuplara ilişkin
kutup frekanslarını hesaplayınız.
Çözüm:
Vo
ri
40
=
=
= 0,8 → ri = 0,8ri + 0,8R g
ri + R g 50
a) V g
0,2ri = 0,8R g → ri = 4R g = 20kΩ
bulunur.
2
2
t ri = 1,1 t rio
+ t rg2 = 300ns → 74380 = 49 + t rio
t rio = 273ns → f ki = 1,287MHz =
Ci =
1
2πf ki (ri // R g )
1
2πC i (ri // R g )
≅ 31pF
değeri elde edilir.
b) Yüksek frekans kutup frekanslarından biri giriş kapasitesinden kaynaklanır ve bu frekans
fki=1,287MHz dir. İkinci kutup çıkış kapasitesinden kaynaklanmaktadır. Çıkışa ilişkin yükselme
süresinden hareketle
2
400 = 1,1 t rio
+ t ro2 + t rg2 → t ro = 240ns
f ko = 1,458MHz
değeri elde edilir.
Soru 29.
a) Açık çevrim gerilim kazancı Ko=100 olan bir kuvvetlendiricinin çıkışına 4kΩ’luk bir yük
direnci bağlandığında devrenin Vo/Vi gerilim kazancı 80’e düşmektedir. Bu devrenin çıkış direnci
nedir?
b) ri=50kΩ olduğuna göre iç direnci Rg olan bir kaynakla sürülen devrenin yük direnci bağlı
iken, kazancının Vo/Vg=50 olması için kaynak direncinin değeri ne olmalıdır?
c) Ci=100pF olduğuna göre, bu devreyi iç direnci çok küçük olan ve yükselme süresi ihmal
edilecek kadar küçük bir darbe kaynağı ile sürülürse çıkışta ölçülen yükselme süresi 50ns
olmaktadır. Osiloskobun yükselme düresi 20ns ise devrenin çıkış kapasitesini hesaplayınız.
29
Çözüm:
a) K′v = 100
Kv = 80
Ry
Ry
→
= 0,8 → R y = 0,8R y + 0,8ro
ro + R y
ro + R y
K v = K v′
0,2R y = 0,8ro → ro =
Ry
4
1kΩ
olarak çıkış direnci elde edilir.
b)
Vo Vo V i
V
ri Vo
ri
=
→ o =
→ 80
= 50
+
+
V g Vi V g
V g ri R g V i
ri R g
1,6ri = ri + R g → R g = 0,6ri = 30kΩ
olarak kaynak iç direnci elde edilir.
2
t ro = 1,1 t ro2 + t ros
= 50
2
⎛ 50 ⎞
c) ⎜ ⎟ = t ro2 + 20 2 → t ro = 40,8ns = 2,2C o (ro // R y )
⎝ 1,1 ⎠
Co =
40,8.10 − 9
= 23,2 pF
2,2.800
olur.
Soru 30.- Şekil 30. deki devrede kullanılan tranzistorlar birbirinin aynıdır. hFE=β=200,
fT=450MHz, Ccb′=0.5pF dır.
Rg
10kΩ
+
Vg
Vi
10k +VCC
RC
CC
T
1
T
Vo
1µF
2
Ry
50kΩ
I
1mA
-VEE
Şekil 30.
a) Orta frekanslara ilişkin Kvo= Vo /Vg kazancını bulunuz.
b) Kuvvetlendiricinin girişine ideal bir basamak işareti uygulandığında çıkıştan alınan işaretin
tr yükselme süresini bulunuz.
c Devrenin girişine, iç direnci aynı değerde fakat f=1kHz’lik kare dalga veren bir sürücü
kaynak bağlandığında darbe üstü eğilmesi ne kadar olur?
d) Devrenin bant genişliğini daha da arttırmak için ne yapılabilir? Devreyi yeniden çizerek
yeni bant genişliğini bulunuz. Bu durumda tr yükselme süresi ne kadar olur?
Çözüm:
a) Tranzistorlar eş olduğundan çalışma noktası akımları bir birine eşittir ve 0,5mA dir. Buna
göre
V
25
= 50Ω
re = T =
I / 2 0,5
30
olur. Kuvvetlendiricinin gerilim kazancı,
R y′
RC // R y
Vo
8333
=
=
=
= 83
2re
2re
2.50
Vi
olarak bulunur. T1 tranzistorunun bazından görülen direnç,
ri = 2hfe re = 2.200.50 = 20kΩ
dir. Vo/Vg gerilim oranı,
Vo
ri Vo 20
=
=
83 = 55,3
V g ri + R g V i
30
biçiminde elde edilir.
b) fT ve re bilindiğine göre,
1
C b ′e =
− C cb ′ = 6,6 pF
2πfT re
dir. Uzun kuyruklu devrenin girişinden görülen eşdeğer kapasite,
C i = C cb ′ +
C b ′e
= 3,8pF
2
olacaktır. Giriş devresinde oluşan kutup frekansı,
0,35
1
1
f ki =
=
= 6,28MHz → t ri =
= 53,7ns
−12
2πC i (R g // ri ) 2π 6667.3,8.10
f ki
çıkış eşdeğer kapasitesi Ccb′ olduğundan
0,35
1
1
f ko =
=
= 38,2MHz → t ro =
= 9,2ns
2πC cb ′ (R y // RC ) 2π 8333.0,5.10 −12
f ko
değerleri elde edilir. Toplam yükselme süresi,
t r = 1,1 t ri2 + t ro2 = 74,3ns
olacaktır.
c) f=1kHz, CC=1µF olarak verildiğine göre kare dalgada darbe süresi ve zaman sabiti,
T
1
TD = =
= 0,5ms τ = C c (RC + R y )
2 2f
olacaktır. Bu büyüklüklerden yararlanılarak darbe üstü eğilmesi için
δ =
TD
0,5.10 −3
= −6
= %0,83
C c (RC + R y ) 10 .60.10 3
değeri elde edilir.
d) Kutup frekanslarından küçük olan giriş devresinde oluşmaktadır. Band genişliğini
arttırmak için devrenin girişine seri olarak L değerinde bir endüktans bağlanmalıdır. Endüktansın
değeri için
L=
R ARB2C i
2ri
bağıntısı kullanılır. Bağıntıda görülen büyüklükler,
R A = R g + ri = 30kΩ R B = R g // ri = 8,33kΩ
dur. Bu değerler kullanıldığında
L=
30.10 3.83332.3,8.10 −12
= 0,2mH
2.20.10 3
C i = 3,8 pF
ri = 20kΩ
31
olarak endüktansın değeri elde edilir. Bu endüktans değeri kullanıldığında giriş devresinde oluşan
2 kadar artacaktır ve fkiL= 2 fki=8,88MHz olur. Bu frekans değeri için
triL=0,35/8.88MHz=39,4ns olacaktır. Çıkışta oluşacak toplam yükselme süresi,
kutup frekansı
tr = 1,1 39,42 + 9,22 = 44,5ns
olacaktır.
Soru 31.- Şekil 31. de kullanılan kuvvetlendiricinin yüksüz gerilim kazancı K=100, giriş
direnci ri=100kΩ, giriş kapasitesi Ci=50pF çıkış direnci de ro=5kΩ dur. Co çıkış kapasitesi ihmal
edilebilmektedir. Zy empedansı devreye bağlandığında orta frekanslardaki Vo/Vg gerilim kazancı 70
olarak ölçülmüştür ve Vo/Vg kazancının üst kesim frekansı 50kHz olmaktadır. Devrenin band
genişliğini arttırmak için bağlanması gereken L endüktansının yerini belirtiniz ve değerini
hesaplayınız.
+
Rg
5kΩ
+
Vg
K
ri
-
Ci
Vo
ro
Zy
Şekil 31.
Çözüm:
Vo/Vg=70 olarak verilmiştir. Devredeki büyüklükler cinsinden bu kazanç,
Ry
Ry
Vo
100 R y
ri
=K
→ 70 = 100
→
= 0,735
105 ro + R y
Vg
ri + R g ro + R y
ro + R y
bağıntısı elde edilir. Bu ilişkiden Ry≅13,87kΩ olarak bulunur. Kuvvetlendiricinin giriş devresinde
oluşan kutup frekansı,
1
f ki =
= 668,5kHz
2πC i (R g // ri )
dır. Üst kesim frekansı 50kHz olarak verilmiştir. baskın kutupla bu frekans belirlenmektedir. Buna
göre çıkış devresinde oluşacak kutup frekansı,
1
1
f ko =
→ Co =
= 866 pF
2πC o (ro // R y )
2πf ko (R y // ro )
olur. Yüke seri olarak değeri L olan bir endüktans bağlanmalıdır. Bu endüktansın değeri,
L=
(ro + R y )(ro // R y ) 2 C o
2R y
= 7,93mH
değeri bulunur.
Soru 32.- Şekil 32. deki devrede kullanılan tranzistorlar birbirinin aynıdır. hFE=β=150,
Ccb’=1 pF, fT=400MHz ve rbb’=50Ω dur.
a) Orta frekanslara ilişkin Kvo=vo/vg kazancını bulunuz.
b) Kuvvetlendiricinin girişine ideal bir basamak işareti uygulandığında çıkıştan alınan işaretin
tr yükselme süresini bulunuz.
c) Devrenin bant genişliğini daha da arttırmak için ne yapılabilir? Devreyi yeniden çizerek
yeni bant genişliğini bulunuz. Bu durumda tr yükselme süresi ne kadar olur?
32
Çözüm:
a) Tranzistorlar bir birine seri bağlanmıştır. Bu nedenle çalışma noktası akımları bir birine
eşittir. Tranzistorların baz akımları ihmal edildiğinde,
R 3VCC
V BB −V BE 1
I C 1 = I C 2 = hFE 1
V BB =
= 4V
RB + (hFE 1 + 1)RE
R1 + R 2 + R 3
RB = R 3 //(R1 + R 2 ) = 5,87kΩ
dur. Akım ifadesinde bilinen değerlerin kullanılması ile IC1=IC2=1,01mA olarak bulunur. Bu akım
değeri için re1=re2=34,75Ω dur. Kaskod kuvvetlendiricinin sağladığı gerilim kazancı ve giriş direnci,
R y′
RC // R y
Vo
=−
=−
= −95,5
r i = R 2 // R 3 // hfe 1re 1 = 1,55kΩ
Vi
re 1
re 1
olacaktır. Bu değerler yardımı ile
R1
18k
RC
6k
T2
CB
Rg
+ 5kΩ
Vg
4kΩ
C1
1µF
8kΩ
R3
C2
+15V
Vo
1µF
R2
10µF
+V CC
Ry
T1
RE
3k3
3,9kΩ
CE
Şekil 32.
Vo
ri V o
=
= −22,62
V g ri + R g V i
bulunur.
b) Tranzistorların fT frekansı yardımı ile
1
C b ′e =
− C cb ′ = 15pF
2πfT re
değeri bulunur. Kaskod kuvvetlendiricinin giriş devresinden görülen eşdeğer kapasite, Ci =
Cb′e+2Ccb′ = 17pF tır.T1 tranzistorunun kolektörüne gelen eşdeğer kapasite, Cb′e dir. Çıkışa gelen
eşdeğer kapasite ise büyük Ccb′ dir. Bu kapasiteler yardımı ile yüksek frekans bölgesinde oluşan
kutup frekansları ve bu frekanslara karşılık gelen yükselme süreleri,
1
0,35
fk1 =
= 7,9MHz → t r 1 =
= 44 ,3ns
2πC i (ri // R g )
f ki
fk 2 =
fk 3 =
1
2πC b ′e re
= 428,7MHz → t r 2 =
0,35
fk 2
= 0,82ns
1
0,35
= 67,3MHz → t r 3 =
= 5,2ns
2πC cb ′ (RC // R y )
fk 3
olurlar. toplam yükselme süresi,
t r = 1,1 t r21 + t r22 + t r23 = 49ns olacaktır.
33
c) Küçük kutup frekansı devrenin girişinde oluştuğundan LC kompanzasyonu devrenin
girişinde yapılmalıdır. Devrenin girişine seri olarak L değerinde bir endüktans bağlanır. Bu
endüktansın değeri,
L=
(R g + ri )(R g // ri )2C i
2ri
= 50,3µH
değeri bulunur. Bu endüktans kullanıldığında giriş devresinde oluşan kutup frekansı
artacak ve bu kutuptan kaynaklanan yükselme süresi de
2 kadar
2 kadar azalacaktır. Buna göre tr1L =
tr1/ 2 =31,3ns olur. Toplam yükselme süresi,
t rL = 1,1 t r21L + t r22 + t r23 = 34,9ns
olacaktır.
Soru 33.- Şekil 35. de kullanılan kuvvetlendiricinin giriş direnci ri çok büyüktür. ro=5kΩ
olarak verilmiştir. Ko=5 ve Z3 yerine değeri 1mH olan bobin kullanıldığına göre devrenin fo=1MHz
de osilasyon yapması için Z1 ve Z2 empedansları yerine kullanılacak reaktif elemanların değerini
hesaplayınız.
Çözüm:
Colpitts osilatöründe
1
C
K o = 1 = 5 fo =
C2
2π L
C 1C 2
C1 + C 2
dir. Bu bağıntıya göre C1 = 5C2 olmaktadır. Frekans ilişkisinden yararlanılarak,
Z3
+
Z1
ri
+
Ko
-
Vo
ro
Z2
Şekil 33.
⎛ 1
⎜⎜
⎝ 2πf o
2
⎞
5
CC
⎟⎟ = L 1 2 = LC 2
C1 + C 2 6
⎠
olur ve C2 kondansatörünün değeri için
6
C2 =
= 30,4 pF
C 1 = 5C 2 = 152pF değerleri bulunur.
5L (2πf o )2
Soru 34- Şekil 34. de görülen dolup-boşalma osilatör devresinde evirmeyen türden bir
Schmitt tetikleme devresi kullanılmıştır. VİH=3V ve VİL=1,5V dur. Çıkıştaki işaretin frekansı f=1kHz
ve darbe boşluk oranı 1/3 ise I1 ve I2 akımlarını hesaplayınız.
Çözüm:
frekans 1kHz, darbe/boşluk oranı=1/3 olarak verilmiş darbe kondansatör boşalırken, boşluk
ise kondansatör dolarken oluşur. Dolma ve boşalma sürelerinin oranı 3’e eşit olmalıdır.
Kondansatör I1 akımı ile dolarken I2 – I1 akımı ile boşalır. Bu süreler,
td =
CVH
I1
tb =
CVH
I 2 − I1
VH = V İH −V İL = 1,5V
34
tur. Süreler oranlanırsa,
td I 2 − I1
=
=3
tb
I 2 = 4I 1
I1
olur. Değişimin frekansı,
+VCC =15V
I1
Vi
+
I2
Vo
C
0,1µF
K
Şekil 34.
f =
1
T
=
1
1
3I 1
=
=
= 1000Hz
tb + td
4t b
4CVH
olacaktır. Buradan hareketle I1=0,2mA ve I2=0,8mA değerleri elde edilir.
Soru35.- Şekil 35. de kullanılan kuvvetlendirici ideal işlemsel kuvvetlendiricidir.
a) Devrenin titreşim (osilasyon) frekansını ve kuvvetlendiricinin kazancını belirleyen b
parametresini veren ifadeleri R, C ve k parametresi cinsinden bulunuz.
b) b=3 ve C=100pF olduğu bilindiğine göre devrenin 100kHz de osilasyon yapması için R’in
değeri ile k parametresini hesaplayınız.
kR
C/k
+
R
C
Vo
-
R1
bR 1
Şekil 35.
Çözüm:
a)Wien osilatörünün hesaplarından görüldüğü gibi,
R
C
1
K = 2 + 1 +1
fo =
R1 C 2
2π R1R 2C 1C 2
dir. Devreden görüldüğü gibi R2/R1=k, C1/C2=k dır. Bu değerler kullanıldığında
1
K = 2k + 1
fo =
2πRC
olur.
b) Devrenin negatif geribeslemeden hareketle sağladığı gerilim kazancı,
35
K =
bR1 + R1
= b + 1 = 2k + 1
R1
dir. b=3 olarak alındığında k=1,5 olacaktır. C=100pF olarak verildiğine göre frekans ilişkisinden
hareketle
1
R =
= 15,92kΩ
2πf oC
biçiminde elde edilir. b=3 için devrenin sağlaması gereken gerilim kazancı K = 4 olmalıdır.