Geometri Notları

www.mustafayagci.com.tr 2013
Geometri Notları
Mustafa YAĞCI, yagcimustafa@yahoo.com
Elips
Koniğin genel tanımını hatırlayarak derse başlayalım: Düzlemde bir F noktası ve F’den geçmeyen bir
d doğrusu verildiğinde, F noktasına uzaklığının d
doğrusuna uzaklığına oranı pozitif bir sabit olan
noktaların geometrik yerine konik deniyordu. Bu
oranı da e ile gösteriyorduk. İşte bu e sayısı (0, 1)
aralığından seçilirse bu noktaların geometrik yeri
bir elips oluyor.
olduğundan üstteki şekilde verilen P1 noktası bulunur. Bu dikme üzerinde başka bir P noktası bulunamaz ama bu dikmenin uzantısında var mıdır?
3k
d
Şimdi F’ye uzaklığı d’ye uzaklığının e katı olan
noktaları işaretleyeceğiz. Anlama ve anlatma kolay1
1
ollığı açısından e’yi şimdilik
alalım. e’nin
2
2
ması, öyle P noktaları bul ki
PF 1
=
Pd 2
olsun, yani
|Pd| = 2⋅|PF|
olsun demektir. Şimdi F’den d’ye bir dik indirelim.
Dikme ayağına da T diyelim.
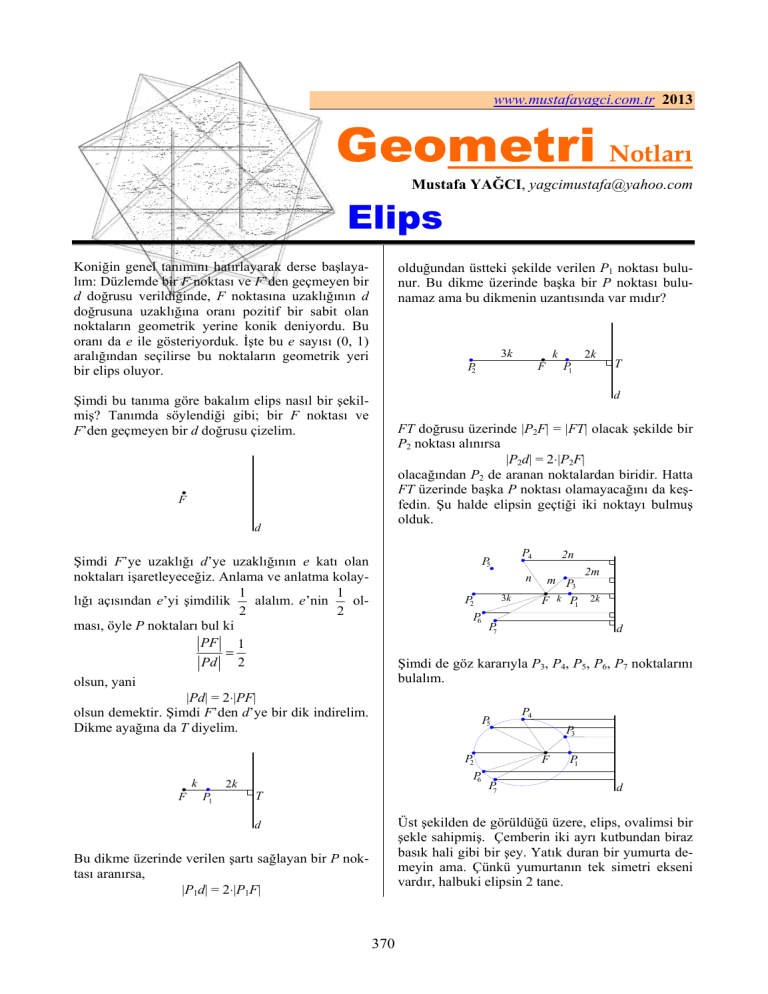
P5
P6
P1
P4
2n
n
m P3
3k
P2
2m
F k P1 2k
P7
d
Şimdi de göz kararıyla P3, P4, P5, P6, P7 noktalarını
bulalım.
P5
P2
F
T
FT doğrusu üzerinde |P2F| = |FT| olacak şekilde bir
P2 noktası alınırsa
|P2d| = 2⋅|P2F|
olacağından P2 de aranan noktalardan biridir. Hatta
FT üzerinde başka P noktası olamayacağını da keşfedin. Şu halde elipsin geçtiği iki noktayı bulmuş
olduk.
F
2k
2k
P1
d
Şimdi bu tanıma göre bakalım elips nasıl bir şekilmiş? Tanımda söylendiği gibi; bir F noktası ve
F’den geçmeyen bir d doğrusu çizelim.
k
k
F
P2
P6
T
P4
P3
F
P7
P1
d
Üst şekilden de görüldüğü üzere, elips, ovalimsi bir
şekle sahipmiş. Çemberin iki ayrı kutbundan biraz
basık hali gibi bir şey. Yatık duran bir yumurta demeyin ama. Çünkü yumurtanın tek simetri ekseni
vardır, halbuki elipsin 2 tane.
d
Bu dikme üzerinde verilen şartı sağlayan bir P noktası aranırsa,
|P1d| = 2⋅|P1F|
370
Mustafa YAĞCI
www.mustafayagci.com.tr
Elips
eşitliğine kavuştuk. P ve Q noktaları rastgele seçildiğinden aslında şunu kanıtlamış olduk:
P2
F
F'
P1
d'
Elips üzerinde alınan herhangi iki noktanın odaklara olan uzaklıklarının toplamı birbirine eşittir.
d
Aslında bu teorem şuna da özdeştir:
Yine üst şekilden görebileceğiniz üzere, kaba şeklini çıkarttığımız elips P1P2 eksenine göre simetrik
olduğundan, F noktası ve d doğrusu yardımıyla bulunan noktaların F′ noktası ve d′ doğrusu yardımıyla da bulunabileceğini fark ediniz. İşte bu yüzden
elipsin 2 tane odağı ve 2 tane doğrultman doğrusu
vardır.
Elips üzerinde alınan bir noktanın elipsin odaklarına olan uzaklıkları toplamı bir sabittir.
Aşağıdaki yorum, bu önemli teoremin aklınızda yer
etmesine yardımcı olacaktır:
F′ ve F noktalarındaki direklerin gevşek bir iple
birbirlerine bağlandıklarını hayal edin.
Elipsin En Önemli Özelliği
Elipsin birazdan vereceğimiz bir özelliği, o kadar
önemlidir ki, çoğu kaynakta bu özelliği elipsin tanımı olarak görmek de mümkündür.
F'
Şimdi elinize bir çubuk alıp bu ipi gerin.
F′ ve F odaklı, bu odaklara ait doğrultmanları da sırasıyla d′ ve d olan rastgele bir elips çizelim. Bu
elipsin üzerinde yine rastgele iki farklı P ve Q noktaları alalım. P’den d ve d′ doğrularına inen dikme
ayakları sırasıyla M ve N, Q’den bu doğrulara inen
dikme ayaklarıysa sırasıyla R ve S olsun.
P v
u
N
eu
F'
S
ey
y
d'
O
F
F'
F
Şimdi de ip gergin kalmak kaydıyla çubuğu hareket
ettirin. Çubuğun ucunun nasıl hareket ettiğini gözlemleyin.
M
ev
ez F
Q
z
R
F'
d
Elipsin tanım gereğince
|PN| = u ise |PF′| = eu,
|PM| = v ise |PF| = ev,
|QS| = y ise |QF′| = ey,
|QR| = z ise |QF| = ez
olacağını biliyoruz. Diğer yandan NSRM dörtgeninin bir dikdörtgen olduğu da ortada. O halde |NM| =
|SR| olması gerektiğinden
u+v=y+z
yazılabilir. Şimdi bu eşitliğin her iki yanını e ile
çarpalım:
eu + ev = ey + ez
olacağından
|PF ′| + |PF| = |QF ′| + |QF|
F
Çubuk yukardaki şekilde nokta nokta olarak gösterilmiş bir eğri çizecektir. İşte bu eğri elipstir. Çubuk
hangi konumda olursa olsun ip gergin olduğundan
çubuğun bulunduğu noktanın direklere uzaklıkları
toplamı ipin boyu kadardır. E ipin uzunluğu sabit
olduğundan çubuğun geçtiği noktaların direğin dikildiği noktalara uzaklıkları toplamının da sabit olduğunu anlarız.
Odak kelimesinin İngilizcesi ‘focus’ olduğundan
genelde odaklar F ve F′ diye gösterilir. Bundan
sonra biz de öyle yapacağız.
371
Mustafa YAĞCI
www.mustafayagci.com.tr
Elips
Şimdi bunun nedenini açıklayalım:
Elipsin Merkezi ve Merkezil Elips
[FF′] doğru parçasının orta noktasına elipsin merkezi denir. Genelde O ile gösterilir.
y
a−c
Bir elips, merkezi analitik düzlemin orijiniyle çakışacak şekilde analitik düzlemde çizilirse bu elipse
merkezil elips denir.
A' F'
-a -c
y
O
-a -c
F A
c
0
a x
B' -b
Elipsin eksenleri kestiği noktalara elipsin köşeleri
denir. Yukardaki elipsin köşeleri
A(a, 0)
A′(−a, 0)
B(0, b)
B′(0, −b)
noktalarıdır. Odakları da
F(c, 0)
F′(−c, 0)
noktalarıdır.
-a
0
-b
a x
c
x
a
Şimdi hep birlikte bir merkezil elipsin denkleminin
nasıl bir şey olduğunu bulacağız. F ve F′ noktaları
orijine göre simetrik olduklarından F′ noktasının
koordinatlarına (–c, 0) dersek, F noktasının koordinatları da (c, 0) olur. Bu noktalara uzaklıkları toplamı 2a br olan noktaların geometrik yer denklemini bulacağız.
y
P(x, y)
Yedek Eksen
Minör Eksen
Küçük Eksen
b
F A
Merkezil Elipsin Denklemi
Odakların üzerinde bulunduğu [AA′] doğru parçasına elipsin asal ekseni, [BB′] doğru parçasına da
elipsin yedek ekseni denir.
y
0
a+c
Teorem, elips üzerindeki herhangi bir nokta için
sağlandığından A noktası için de sağlanmalıdır. Şu
durumda
|AF| + |AF′|
toplamı aradığımız sabiti verecektir.
|AF| = a – c
|AF′| = a + c
olduğundan
|AF| + |AF′| = 2a
olduğu kanıtlanmış olur.
B b
A' F'
O
F'(−c, 0)
Asal Eksen
Majör Eksen
Büyük Eksen
0
F(c, 0)
x
Elips üzerindeki herhangi bir noktanın koordinatlarını (x, y) olarak alalım. Bu noktanın odaklara olan
uzaklıkları toplamı 2a br olması gerektiğinden
Asal eksene majör eksen veya büyük eksen, yedek eksene de minör eksen veya küçük eksen de
denir.
( x + c) 2 + y 2 + ( x − c ) 2 + y 2 = 2a
yani
Asal eksenin önemi, daha çok uzunluğunda yatar.
Hani demiştik ya, elips üzerindeki herhangi bir
noktanın elipsin odaklarına olan uzaklıklarının toplamı bir sabittir, işte o sabit asal eksenin uzunluğudur yani üstteki gösterime göre 2a’dır.
x 2 + 2cx + c 2 + y 2 + x 2 − 2cx + c 2 + y 2 = 2a
eşitliği sağlanmalıdır.
İşlem kolaylığı açısından x2 + c2 + y2 = m diyelim.
m + 2cx + m − 2cx = 2a
372
Mustafa YAĞCI
www.mustafayagci.com.tr
Elips
Eğer bir merkezil elipsin odakları x ekseni üzerinde
değil de y ekseni üzerindeyse, denklemi yine
x2 y 2
+
=1
a2 b2
olur fakat bu sefer
b2 = a 2 + c 2
eşitliği sağlanır. Zira bu sefer ipin boyu 2a değil, 2b
olmaktadır.
Şimdi her iki yanın karesini alalım.
m + 2cx + m − 2cx + 2 m + 2cx m − 2cx = 4a 2
2m + 2 m + 2cx m − 2cx = 4a 2
m + m + 2cx m − 2cx = 2a 2
m + 2cx m − 2cx = 2a 2 − m
(m + 2cx)(m − 2cx) = 4a 4 − 4a 2 m + m 2
m 2 − 4c 2 x 2 = 4 a 4 − 4 a 2 m + m 2
2
2
4
b
2
−4c x = 4a − 4a m
y
c
−c 2 x 2 = a 4 − a 2 m
b
Şimdi m yerine gerçek değerini tekrar yazıp düzenleyelim.
-a
a
0
x
b
−c 2 x 2 = a 4 − a 2 x 2 − a 2 c 2 − a 2 y 2
-c
(a 2 − c 2 ) x 2 + a 2 y 2 = a 4 − a 2 c 2
-b
(a 2 − c 2 ) x 2 + a 2 y 2 = a 2 (a 2 − c 2 )
Genel olarak; a2 > b2 ise odaklar x ekseni üzerinde,
b2 > a2 ise odaklar y ekseni üzerinde diyebiliriz.
Şimdi eşitliğin her iki yanını a 2 (a 2 − c 2 ) ’ye bölelim.
x2
y2
+
=1
a2 a2 − c2
Alıştırmalar. Aşağıdaki tabloda boş bırakılan kutuları grafiğe bakarak doldurunuz.
Sonuca ulaştık ama ufak bir hamle daha kaldı.
y
B3
y
P
a
F
c
b
0
A' F'
a
c
F'
x
Denklemi
P
F A
5
0
x
B'
A( ,
), A'(
, )
B( ,
), B'(
,
Yedek eksen uzunluğu:
F(
Odaklar arası uzaklık:
|PF| + |PF '|
y
B
,
)
P
0
B'
Asal eksen uzunluğu:
373
, ), F '(
Denklemi
A' F'
Uzun lafın kısası: x2’nin paydasına x eksenini kestiği noktaların apsislerinin karesini, y2’nin paydasına
da y eksenini kestiği noktaların ordinatlarının karesini yazıp toplayıp 1’e eşitliyoruz.
)
Elipsin odakları
Asal eksen uzunluğu:
P noktasını elipsin en üst köşesi olarak alırsak F′PF
ikizkenar üçgen olacağından |F′P| = |PF| = a br
olur. Diğer yandan |FO| = |OF′| = c br olduğundan
|OP|2 = b2 = a2 – c2 olur. Şu durumda elips denklemi
x2 y 2
+
=1
a2 b2
halini alır.
Elipsin köşeleri
F A
15 17
x
Elipsin köşeleri
A( ,
), A'(
, )
B( ,
), B'(
,
)
Elipsin odakları
Yedek eksen uzunluğu:
F(
, ), F '(
Odaklar arası uzaklık:
|PF| + |PF '|
,
)
Mustafa YAĞCI
www.mustafayagci.com.tr
y
Örnek.
Denklemi
B
Elips
4x2 + 25y2 = 100
elipsinin odaklar arası uzaklığı kaç birimdir?
P
10
A' F'
F A
8
0
B'
x
A( ,
), A'(
, )
B( ,
), B'(
,
F(
Odaklar arası uzaklık:
|PF| + |PF '|
A
0
F'
x
P
2B
3F
A
0
F'
x
P
B'
Elipsin köşeleri
A( , ), A'( , )
B( , ), B'( , )
Elipsin odakları
F( , ), F '( , )
Örnek. A(8, 0) ve B(−8, 0) noktalarına uzaklıkları
toplamı 20 br olan noktaların geometrik yer denklemi aşağıdakilerden hangisidir?
Asal eksen uzunluğu
Yedek eksen uzunluğu
Odaklar arası uzaklık
y
B
F
A
6 x
P
B'
|PF| + |PF '|
x2 y2
+
= 1 ola2 b2
sun. Üzerinden geçtiği söylenen noktaların denklemi sağlamasını bekleyelim. O halde
9 32
+
=1
a2 b2
36 20
+
=1
a2 b2
eşitlikleri birlikte sağlanmalıdır. Üstteki eşitliğin 4
katından alttaki eşitlik çıkartılırsa b2 = 36 bulunur.
Bu değer de eşitliklerin herhangi birinde yerine yazılırsa a2 = 81 bulunur. Şu durumda a = 9 olacağından asal eksen uzunluğu 2a = 18 birimdir.
Çözüm: Merkezi elipsin denklemi
Denklemi:
|PF| + |PF '|
F'
Örnek. P (3, 4 2) ve Q (6, 2 5) noktalarından
geçen merkezil elipsin asal eksen uzunluğu kaç birimdir?
Elipsin köşeleri
A( , ), A'( , )
B( , ), B'( , )
Asal eksen uzunluğu
Yedek eksen uzunluğu
Odaklar arası uzaklık
y
0
)
Denklemi:
|PF| + |PF '|
A'
,
Elipsin odakları
F( , ), F '( , )
−5 B'
A'
, ), F '(
Asal eksen uzunluğu
Yedek eksen uzunluğu
Odaklar arası uzaklık
B
F
A'
−3
)
Elipsin odakları
Asal eksen uzunluğu:
Yedek eksen uzunluğu:
y
Çözüm: Öncelikle eşitliğin her iki yanını 100’e bölerek denklemi bildiğimiz formata getirelim:
x2 y 2
+
=1
25 4
olacağından anlıyoruz ki a = 5 ve b = 2’ymiş. Bu
değerler c2 + b2 = a2 denkleminde yerlerine yazılırsa c2 = 21 bulunacağından c = 21 olur. O halde
odaklar arası uzaklık 2c = 2 21 olarak bulunur.
Elipsin köşeleri
10
Çözüm: Verilmiş farklı iki noktaya uzaklıkları toplamı sabit olan noktalar kümesinin elips olduğunu
bilmekteyiz. Demek ki A ve B noktaları bu elipsin
odaklarıdır. Yani c = 8’miş. Diğer yandan ipin
uzunluğu 2a = 20 br olarak verildiğinden a = 10 çıkar. c2 + b2 = a2 denkleminden de b = 6 bulunacağı
için geometrik yer denklemi
x2 y2
+
=1
100 36
olmalıdır.
Elipsin köşeleri
A( , ), A'( , )
B( , ), B'( , )
Elipsin odakları
F( , ), F '( , )
Denklemi:
374
Mustafa YAĞCI
www.mustafayagci.com.tr
Elipsin Doğrultmanları ve Dışmerkezliği
Örnek.
9x2 + 25y2 = 900
elipsinin doğrultmanlarının arasındaki uzaklık kaç
birimdir?
Merkezil bir elipsin denklemini bulduk, şimdi sıra
bu elipsin doğrultmanlarının denklemi ile dışmerkezliğini bulmaya geldi. Elipsin tanımı gereğince,
elips üzerindeki her noktanın bir odağına olan uzaklığının o odağa ait doğrultmana olan uzaklığına
oran sabittir.
Çözüm: Öncelikle eşitliğin her iki yanını 900’e bölerek denklemi bildiğimiz formata getirelim:
x2 y2
+
=1
100 36
olacağından anlıyoruz ki a = 10 ve b = 6’ymış. Bu
değerler c2 + b2 = a2 denkleminde yerlerine yazılırsa c2 = 64 bulunacağından c = 8 olur. Diğer yandan
doğrultmanlar arası uzaklık 2t olup
a 2 100
t=
=
= 12,5
8
c
olduğundan 2t = 25 olarak bulunur.
Şu halde elips üzerinde iki farklı P ve Q noktası
alıp bu oranları eşitleyelim. P ve Q noktalarını alelade alırsak işimiz zorlaşır. Bu yüzden bu noktaları
köşelerden seçmekte fayda var. Önce P = A olsun.
y
B b
t
Elips
L
a
D' A' F'
-t -a -c
0
F A D
c a t x
Örnek. F(4, 0) odağına ait doğrultmanının denklemi 4x = 25 olan merkezil elipsin dışmerkezliği
kaçtır?
B' -b
F odağına ait doğrultmana x = t doğrusu diyelim.
Tanım gereği
PF
AF a − c
=
=
e=
PD
AD t − a
olur. Şimdi de Q = B olsun. Yine tanım gereği
QF
BF a
e=
=
=
QL
BL t
olur. Şu durumda bu e değerleri birbirine eşittir.
a−c a
=
t−a t
at − ct = at − a 2
Çözüm: Odağın koordinatlarından c = 4 olduğunu,
doğrultman denkleminden de
a 2 25
t=
=
4
c
olduğundan dolayı a = 5 olduğunu anlıyoruz. Şu
durumda
c 4
e= =
a 5
olarak bulunur.
Örnek. Dışmerkezliği 0,5 ve F′ odağına ait doğrultmanının denklemi x = 12 olan merkezil elipsin
yedek eksen uzunluğu kaç birimdir?
ct = a 2
a2
c
demek ki elipsin doğrultmanlarının denklemleri
a2
x=
c
imiş. Şimdi de e’yi (dışmerkezliği) bulalım.
a a c
e= = 2 = .
t a
a
c
t=
Çözüm: Dışmerkezliği veren formül olan
c 1
e= =
a 2
eşitliğinden a = 2c olduğunu anlıyoruz. Diğer yandan
a 2 4c 2
t=
=
= 4c = 12
c
c
olduğundan dolayı c = 3 olduğunu anlıyoruz. O
halde a = 6 olup c2 + b2 = a2 denkleminde yerlerine
yazılırsa b2 = 36 – 9 = 27 bulunacağından b = 3 3
Bu değer elipsin çemberden ayrılış derecesini gösterir. Elips; a sabitken c = 0 olduğunda çember olur,
c = a olduğunda doğru parçası olur. Yani e’nin küçülmesi elipsi kalınlaştırır, büyümesi elipsi inceltir!
olur. Yedek eksen uzunluğu da 2b yani 6 3 olur.
375
Mustafa YAĞCI
www.mustafayagci.com.tr
Elips
Elipsin Parametresi (Latus Rectum)
Elipsin Odaksal Parametresi
Elipsin, çıkardığımız denkleminden de anlaşılacağı
üzere, belirlenebilmesi için birbirinden bağımsız en
az iki bilgiye ihtiyaç duyulur. Sadece odaklarını
bilmekle bir elips belirlenemeyeceği gibi sadece
dışmerkezliğiyle de belirlenemez. Şimdi bunların
yanına bir de elipsin kalınlığını (şişkinliğini) anlatan üç bilgi daha vereceğiz.
Bir elipsin herhangi bir odağının o odağa ait doğrultman doğrusuna uzaklığına elipsin odaksal parametresi denir.
İngilizce’si focal parameter olarak bilinir. Genelde
l ile gösterilir.
Odakların birinden geçen ve asal eksene dik olan
kirişin uzunluğuna elipsin parametresi denir.
b
Tüm kaynaklarda latus rectum olarak geçer. Genelde p ile gösterilir. Yarısına da semi-latus rectum
denir.
−a
Bakalım bir merkezil elips için bu sayı kaça eşitmiş.
y
b
0
a x
F(c, 0)
F odağından çıkan dikmenin elipsi kestiği noktaya
P diyelim. Elipsin parametresine p dersek
p
PF =
2
olduğu aşikar. Diğer yandan
PF ' + PF = 2a
olduğunu da biliyoruz. O halde
p
PF ' = 2a −
2
olur. F ' F = 2c eşitliğini kullanarak F ' FP dik
üçgeninde Pisagor teoremi yazalım.
2
l
D
t x
Not: Bir elipsin dışmerkezliğini daha önceden
c
e=
a
bağıntısıyla vermiştik. Şimdi parametreleri cinsinden de verebiliriz:
b2
p
c a
p
e= = 2 = 2 =
a b
l 2l
c
olduğundan yarım parametrenin (semi-latus rectum) odaksal parametreye bölümünün de dışmerkezliği verdiğini görmüş oluyoruz. Bir başka deyişle; aşağıda resmedildiği üzere
-b
y
b B
2
p
p
( 2c ) +   =  2a − 
2
2 
2
p
p2
= 4a 2 − 2ap +
4c 2 +
4
4
2
2
2ap = 4a − 4c
2
F
c
0
Yukardaki şekilden de görüleceği üzere, odaksal
parametrenin değeri |FD| olup
a2
a 2 − c2 b2
=
FD = l = t − c = − c =
c
c
c
formülüyle hesaplanır.
P(x, y)
-a F'(−c, 0)
y
θ
A'
F'
−a −c
0
P
p
2
F
B'
2ap = 4b 2
hem
2b 2
p=
a
hem de
bağıntısı geçerlidir.
376
e = sin θ
e = tan α
α
l
Dx
Mustafa YAĞCI
www.mustafayagci.com.tr
Elipsin Basıklık Oranı
Elips
y
Aynen parametre ve odaksal parametre gibi, elipsin
şişkinliğini anlatan bir değer daha vardır. Diğerlerine göre pek önem taşımaz. Şimdi onu verelim:
Doğrultman Denklemleri
B
F
A'
−3
Büyük eksen uzunluğu ile küçük eksen uzunluğu
farkının büyük eksen uzunluğuna oranı elipsin basıklığı diye bilinir. Yani elipsin basıklığı,
2a − 2b a − b
b
q=
=
=1−
2a
a
a
sayısıdır.
A
0
F'
Dışmerkezliği
x
P
Parametresi
Odaksal parametresi
−5 B'
Basıklık oranı
y
Doğrultman Denklemleri
2B
3F
A'
Alıştırmalar. Aşağıdaki tabloda boş bırakılan kutuları grafiğe bakarak doldurunuz.
y
B3
A'
F'
F A
5
0
B
x Dışmerkezliği
A' F'
F A
15 17
0
A'
0
y
B'
Odaksal parametresi
Doğrultman Denklemleri
A
6 x
P
|PF| + |PF '|=10
Dışmerkezliği
Parametresi
Odaksal parametresi
Basıklık oranı
9x2 + 25y2 = 225
elipsinin parametresini, odaksal parametresini ve
basıklık oranını bulalım.
Çözüm: Öncelikle eşitliğin her iki yanını 225’e bölerek denklemi bildiğimiz formata getirelim:
x2 y 2
+
=1
25 9
olacağından anlıyoruz ki a = 5 ve b = 3’müş. Bu
değerler c2 + b2 = a2 denkleminde yerlerine yazılırsa c2 = 16 bulunacağından c = 4 olur. O halde
2b 2 18
b 2 18 9
a −b 2
= , l = = = ve q =
p=
=
5
a
c
a
5
4 2
olarak bulunur.
Doğrultman
Denklemleri
P
0
Basıklık oranı
Örnek.
x Dışmerkezliği
10
A' F'
Odaksal parametresi
Basıklık oranı
Odaksal parametresi
B
B'
Parametresi
B'
Parametresi
F
Doğrultman
Denklemleri
P
P
y
F'
y
x
B
Basıklık oranı
Odaksal parametresi
Dışmerkezliği
B'
Parametresi
B'
0
F'
Doğrultman
Denklemleri
P
A
F A
8
x Dışmerkezliği
Parametresi
Basıklık oranı
377
Mustafa YAĞCI
www.mustafayagci.com.tr
Elips
Yarım Elips Denklemleri

y2 
x = ± a 2 1 − 2 
 b 
eşitliği elde edilir ki, + ve − ifadelerinin birinin seçimiyle bu denklem de bir tam elipsin değil bir yarım elipsin denklemi olur. Ama bu sefer üst-alt yarım elipslerinin değil de sağ-sol yarım elipslerinin!
x2 y 2
+
=1
a2 b2
elipsini oluşturan yaylarının aynen çemberde olduğu gibi ayrı ayrı denklemleri vardır. Örneğin,
yukardaki denklemi
y2
x2
=1− 2
2
b
a
diye, ardından da

x2 
y 2 = b2 1 − 2 
 a 
Çünkü

y2 
x = a 2 1 − 2 
 b 
eşitliğini sağlayan x değerleri hiçbir zaman negatif
olamaz. Bu yüzden grafik
diye düzenlersek grafikte hiçbir değişiklik olmaz.
Fakat,
 x2 
y = b 2 1 − 2 
 a 
dendiği anda grafik artık bir elips çizmez. Çizer de
tam bir elips olmaz, yarım elipstir bunun grafiği.
Çünkü bu denklemde y’ler hiçbir zaman negatif
olamaz.
y
b
a
0
x
−b
y
b
yukardaki gibi olur.
−a
a
0
x
Benzer şekilde

y2 
x = − a 2 1 − 2 
 b 
eşitliğini sağlayan x değerleri hiçbir zaman pozitif
olamaz. Bu yüzden grafik
Yani merkezil bir elipsin üst yarısının denklemidir
bu.
Benzer şekilde
 x2 
y = − b 2 1 − 2 
 a 
eşitliğini sağlayan y değerleri de hiçbir zaman pozitif olamaz.
y
b
−a
y
−a
a
0
x
0
−b
x
−b
yukardaki gibi olur.
Her bağıntı grafiği gibi, elips ve yarım elips grafikleri de ötelenebilir, döndürülebilir. Eğer grafik a birim sağa kayarsa x yerine x – a, sola kayarsa x yerine x + a, yukarı kayarsa y yerine y – a, aşağı kayarsa da y yerine y + a yazarız. Tabii döndürme olayının uygulaması bu kadar basit değil diye o kısmı
konunun sonuna sakladık. Merak edin biraz!
Bu yüzden bu denklem de merkezil bir elipsin alt
yarısının denklemidir.
Eğer elips denklemini

x2
y2
y2 
= 1 − 2 yani x 2 = a 2 1 − 2 
2
a
b
 b 
şeklinde düzenleyip
378
MY GEO 3
KONİKLER
TEST 155
Mustafa YAĞCI
Elipsin merkezi, odakları, eksenleri
CACECAA
1.
5.
Odakları F(−3, 2) ve F′(5, 6) olan elipsin merkezinin koordinatları hangi şıkta verilmiştir?
Odaklarından biri (−4, 0),
köşelerinden biri de (0, 3)
olan merkezil elips üzerinde bir P noktası alınıyor.
P noktasının elipsin
odaklarına olan uzaklıkları toplamı kaç br dir?
A) (0, 0)
B) (1, 2)
D) (−1, 4)
C) (1, 4)
E) (1, 8)
A) 7
B) 9
C) 10
y
-4
3
P
0
D) 12
x
E) 14
2.
Majör ekseninin boyu 10 br, minör ekseninin
boyu 6 br olan merkezil elipsin denklemi aşağıdakilerden hangisidir?
A)
x2 y 2
x2 y 2
x2 y 2
+
= 1 B)
+
= 1 C)
+
=1
25 9
9 25
25 16
x2 y 2
x2 y 2
+
=1
E)
+
=1
D)
16 25
9 16
6.
F(−4, 0) ve F′(4, 0) noktalarına uzaklıkları toplamı 10 br olan noktaların geometrik yer denklemi aşağıdakilerden hangisidir?
A)
3.
x2 y 2
x2 y 2
x2 y 2
+
= 1 B)
+
= 1 C)
+
=1
25 9
9 25
25 16
x2 y 2
x2 y 2
+
=1
E)
+
=1
D)
16 25
9 16
x2 y 2
=1
+
25 16
elipsi üzerindeki bir noktanın odaklara uzaklıkları toplamı kaç birimdir?
A) 25
B) 16
C) 10
D) 5
E) 4
7.
4.
5x2 + 16y2 = 80
denklemli elipsin odaklarının arasındaki uzaklık
kaç birimdir?
A) 11
y
Yandaki elipsin alt ve üst
köşeleriyle odak noktaları0
nın belirttiği dörtgenin çevresi 52 br ve alanı 120 br2
dir.
Buna göre elipsin denklemi aşağıdakilerden
hangisi olabilir?
B) 13
C) 4
D)
21
E)
A)
44
379
x
x2
y2
x2
y2
x2
y2
+
= 1 B)
+
= 1 C)
+
=1
169 25
144 25
25 144
x2 y 2
x2
y2
+
=1
+
=1
E)
D)
13 5
144 169
MY GEO 3
KONİKLER
TEST 156
Mustafa YAĞCI
Elipsin merkezi, odakları, eksenleri
EBABCA
1.
4.
Odak noktaları F ve F′,
y
P
x2 y 2
+
=1
denklemi de
25 9
F
F' x
0
olan yandaki elipsin üzerinde bir P noktası alınıyor.
Buna göre F′PF üçgensel bölgesinin alanı aşağıdakilerden hangisi olamaz?
A) 9
B) 10
C) 11
D) 12
x2
y2
+
=1
4a 2 a 2
olan yandaki elipsin odaklarıyla üst köşesinin belirttiği geniş açının ölçüsü
α°’dir.
Buna göre α kaçtır?
A) 105
2.
B) 7
C) 8
B) 120
α
0
C) 135
x
D) 150
E) 165
E) 13
5.
Odak noktaları F ve F′
y D
olan yandaki merkezil
d
elipsin köşeleri şekilde
A 2F 5 O
görüldüğü üzere A, B, C
ve D noktalarıdır.
B
|AF| = 2 br
|FO| = 5 br
olduğuna göre |DF| = d kaç br dir?
A) 6
y
Denklemi
Büyük eksen köşeleri A(5, 0), A′(−5,0) olan ve
D(−4, 12/5) noktasından geçen merkezil elipsin
denklemi aşağıdakilerden hangisidir?
x
F' C
A)
D) 9
E) 10
x2
x2 y 2
x2 y 2
+ y 2 = 1 B)
+
= 1 C)
+
=1
25
25 18
25 16
x2 y 2
x2 y 2
D) +
=1
E)
+
=1
25 25
25 12
6.
3.
Odaklarından birinin orijine uzaklığı 3 br, elipse
en yakın uzaklığı da 1 br
olan merkezil elipsin
denklemi aşağıdakilerden
hangisidir?
y
y
P
3
1
x
F
0
F'
x
Şekildeki merkezil elipsin denklemi
9x2 + 16y2 = 144
ise Ç(PFF′) değeri aşağıdakilerden hangisidir?
x2 y 2
x2 y 2
x2 y 2
+
=1
B)
+
= 1 C)
+
=1
A)
16 7
16 8
16 9
x2 y 2
x2 y 2
+
=1
+
=1
E)
D)
16 10
16 12
A) 8 + 2 7
380
B) 6 + 2 7
C) 10
D) 6
E) 4
MY GEO 3
KONİKLER
TEST 157
Mustafa YAĞCI
Elipsin merkezi, odakları, eksenleri
CCDEBDB
1.
4.
F(−4, 0) ve F(4, 0) noktalarına olan uzaklıkları
toplamı 10 birim olan noktaların geometrik yer
denklemi aşağıdakilerden hangisidir?
y
P
F
0
F'
Şekilde F ve F′ noktaları
x
A)
x2
y2
+
= 1 elipsinin
169 144
x2 y 2
x2 y 2
x2 y 2
+
= 1 B)
+
= 1 C)
+
=1
9 16
16 9
25 10
x2 y 2
x2 y 2
+
=1
+
=1
D)
E)
10 6
25 9
odaklarıdır.
Ç(PFF’) değeri aşağıdakilerden hangisidir?
A) 28
B) 32
C) 36
D) 40
E) 44
5.
x eksenini asal eksen kabul eden ve asal eksen
uzunluğu 10 birim, yedek eksen uzunluğu 8 birim olan elipsin odaklar arası uzaklığı kaç birimdir?
A) 6 5
2.
B) 6
C) 5
D) 4
E) 3
F ve F′ bir elipsin odak noktalarıdır.
F′(−8, 0) ve F(8, 0) noktalarına uzaklıklarının
toplamı 24 birim olan elipsin denklemi aşağıdakilerden hangisidir?
A)
x2 y 2
x2 y 2
x2
y2
+
= 1 B)
+
= 1 C)
+
=1
121 40
121 30
144 80
x2
y2
x2
y2
D)
+
=1
E)
+
=1
144 30
144 36
6.
Yedek ekseni y−ekseni olan merkezil elipste
M(−15, 0) ve N(0, 12)
noktaları birer köşe koordinatıdır.
Buna göre bu elipsin odaklarından birisinin koordinatları aşağıdakilerden hangisidir?
A) (0, 5) B) (0, 9) C) (5, 0) D) (9, 0) E) (3, 0)
3.
Aşağıdaki denklemlerden hangisi asal eksen
uzunluğu 82 birim ve odaklar arası uzaklığı 18
birim olan elipse aittir?
A)
7.
Odaklarından birisinin koordinatları F (3 2,0) olan
merkezil elips P(2, 4) noktasından geçmektedir.
Buna göre bu elipsin asal eksen uzunluğu kaç
birimdir?
x2 y 2
x2 y 2
x2 y 2
+
=1
+
= 1 C)
+
=1
B)
82 18
41 9
41 40
x2
y2
x2
y2
+
=1
+
=1
D)
E)
1681 1600
1600 81
A) 6
381
B) 12
C) 13
D) 15
E) 18
MY GEO 3
KONİKLER
TEST 158
Mustafa YAĞCI
Tam ve Yarım Elips Denklemleri
ADEEBAA
1.
5.
10
, 2) noktalarından geçen
A( 5, 1) ve B(
2
merkezil elipsin denklemi aşağıdakilerden hangisidir?
Denklemi 9 x 2 + 25 y 2 = 225
T
P
olan elipsin üst köşesi olan
0
T noktasından elipse çizilen
2
2
x
y
+
=1
teğet, denklemi
100 36
olan elipsi P ve Q noktalarında kesmektedir.
Buna göre |PQ| kaç birimdir?
A) 2x2 + 5y2 = 15
C) 5x2 + 2y2 = 10
E) 2x2 + y2 = 5
B) 3x2 + 5y2 = 15
D) x2 + 5y2 = 10
A) 18
y
C) 16
B) 10 3
Q
x
D) 8 3
E) 15
2.
Çember için aşağıdakilerden hangisi söylenebilir?
A) Dış merkezliği 1 olan elipstir.
B) Doğrultmanı x ekseni olan elipstir.
C) Doğrultmanı y ekseni olan elipstir.
D) Odakları çakışık olan elipstir.
E) Basıklık oranı 1 olan elipstir.
6.
Yanda grafiği vey
rilen yarım elipsin odaklarından
biri (3, 0) noktasındadır.
x
0
−6
3 4
O halde yarım
elipsin denklemi aşağıdakilerden hangisidir?
3.
y
Odak noktaları F ve F′,
P
2
2
x
y
+
=1
denklemi de
25 9
F
F'
x
0
olan yandaki elipste F′
noktasından x eksenine çıkılan dikme, elipsi P noktasında kesmektedir.
Buna göre |PF′| kaç birimdir?
A) 1
B)
6
5
C)
7
5
D)
8
5
E)
3
24 − 2 x − x 2
5
3
24 − 2 x − x 2
C) y =
4
4
E) y =
15 − 2 x − x 2
5
A) y =
4
24 − 2 x − x 2
5
3
D) y =
15 − 2 x − x 2
5
B) y =
9
5
7.
4.
2
y
2
Yanda grafiği verilen yarım elipsin denklemi aşağıdakilerden hangisidir?
P
x
y
+
= 1 olan
25 9
x
A
0
elipsin sağ köşesi olan A
noktasından x eksenine çıkılan dikme, denklemi
x2
y2
+
= 1 olan elipsi P noktasında kesmektedir.
100 36
Buna göre |PA| kaç birimdir?
Denklemi
A) 2 3
B) 13
C) 4
D) 3 2
y
−4
3
16 − x 2
5
3
16 − x 2
C) y = −1 −
4
4
16 − x 2
E) y = −1 −
3
A) y = −1 −
E) 3 3
382
0
−1
4
x
−4
4
16 − x 2
5
3
16 − x 2
D) y = −1 +
4
B) y = −1 −
MY GEO 3
KONİKLER
TEST 159
Mustafa YAĞCI
Elipsin Parametresi, Doğrultmanları, Dışmerkezliği
DDDABACA
1.
5.
x2 y 2
+
=1
81 45
elipsinin parametresi kaç birimdir?
x2
y2
+
=1
100 25
elipsinin odaklarının birinden geçen en kısa kiriş
ile en uzun kirişin boylarının toplamı kaç birimdir?
A) 1
B) 2
C) 5
D) 10
E) 15
A) 24
2.
9x2 + 16y2 = 144
elipsinin parametresi kaçtır?
A) 3
B)
7
2
C) 4
B)
2
3
C)
3
4
D) 27
E) 28
D)
9
2
x2 + 2y2 = 8
elipsinin doğrultmanlarından biri aşağıdakilerden hangisidir?
E) 5
A) x = 4
B) x = 3 C) x = 2 D) y = 3 E) y = 4
7.
x2 y 2
+
=1
25 9
elipsinin dış merkezliği kaçtır?
1
2
C) 26
6.
3.
A)
B) 25
Odaklarından birisi F(4, 0) olan elipsin doğrultmanlarından birinin denklemi x = 9 ise dış
merkezliği kaçtır?
D)
4
5
E)
3
5
A)
5
3
B)
4
3
C)
2
3
D) 1
E) 2
8.
4.
x
y
+
=1
36 324
elipsinin odaklarının birinden geçen en kısa kirişin boyu kaç br dir?
x2
y2
+
=1
256 400
elipsinin bir odağının doğrultmanlardan birine
uzaklığı kaç birim olabilir?
A) 4
A)
2
B) 5
2
C) 6
D) 7
E) 8
383
64
3
B)
61
3
C) 19
D)
47
3
E) 13
MY GEO 3
KONİKLER
TEST 160
Mustafa YAĞCI
Elipsin Parametresi, Doğrultmanları, Dışmerkezliği
AABDED
1.
4.
x2 y 2
+
=1
25 9
elipsinin doğrultmanlarının denklemleri hangi
şıkta verilmiştir?
Odak noktaları x ekseni üzerinde ve büyük eksen
uzunluğu 12 birim olan merkezil bir elipsin, odaklarının birinden büyük eksene çizilen dik kirişin
uzunluğu 8 birimdir.
Bu elipsin denklemi aşağıdakilerden hangisidir?
A) x = ±
25
4
B) x = ±
D) x = ±
25
9
25
3
C) x = ±6
E) x = ±
A)
29
6
x2 y2
x2 y 2
x2 y 2
+
= 1 B)
+
= 1 C)
+
=1
36 4
25 64
5 16
x2 y2
x2 y2
+
= 1 E)
+
=1
D)
36 24
36 64
5.
x = 4 doğrusuna uzaklığı, F(−2, 0) noktasına
uzaklığının iki katına eşit olan noktaların geometrik yerinin denklemi aşağıdakilerden hangisidir?
2.
Denklemi x2 + 4y2 = 64 olan elipsin doğrultman
denklemlerinden biri aşağıdakilerden hangisi
olabilir?
A) x = −
16 3
3
D) x =
B) x = −
8 3
3
4 3
3
E) x =
C) x = −
4 3
3
A)
8 3
3
x2 y 2
x2 y 2
x2 y 2
+
= 1 B)
+
= 1 C)
+
=1
4
3
81 64
9 12
( x + 4) 2 y 2
( x + 4) 2 y 2
D)
+
= 1 E)
+
=1
8
18
16
12
6.
Yanda sağ köşesi (8, 0) ve
y
6
üst köşesi (0, 6) olan bir
d
merkezil elips ve bu nokta8 x
lardaki teğetleri ve eksen0
lerle oluşturulmuş bir dikdörtgen bulunmaktadır.
Dikdörtgenin köşegeninin elips içinde kalan
kısmının boyu kaç br dir?
3.
Konumu bilinmeyen bir elipsin asal eksen uzunluğunun 50 br, yedek eksen uzunluğunun da 14 br olduğu bilinmektedir.
Buna göre bu elipsin dış merkezliği kaçtır?
A)
625
576
B)
24
25
C)
576
625
D)
7
24
E)
7
25
A) 4
384
B) 4 2
C) 5
D) 5 2
E) 6
MY GEO 3
KONİKLER
TEST 161
Mustafa YAĞCI
Elipsin Parametresi, Doğrultmanları, Dışmerkezliği
CBEACB
1.
4.
O merkezli, F ve F′
odaklı yandaki elipste
d doğrultmanlardan
biridir. F’nin apsisi 4,
sağ köşenin apsisi 6,
d’nin x eksenini
kestiği noktanın
apsisi de k’dir.
Buna göre k kaçtır?
A) 7
B) 8
y
O merkezli
y
yandaki elipste, d'
5
P
D'
F ve F′
6
odaklarına ait
3
doğrultmanlar
O
F'
sırasıyla d ve d′
doğrularıdır.
|PD′| = 5 birim
|PF′| = 3 birim
|PF| = 6 birim
olduğuna göre |PD| kaç birimdir?
d
F'
F
O
C) 9
4
k
6
D) 10
x
E) 12
A) 10
2.
O merkezli, F ve F′
odaklı yandaki elipste
d doğrultmanlardan biridir.
BF ⊥ FC
F'
BC ⊥ d
m(FCB) = 45°
olduğuna göre
AD
oranı kaçtır?
AF
A) 1
B)
2
C)
3
2
B
o
45
O
F A
D)
C) 4
D) 13
x
E) 15
O merkezli
y
d
yandaki elipste, d'
B
10
P
D
D'
F ve F′
5 L
odaklarına ait
6
x
doğrultmanlar
O
F A K x
F'
sırasıyla d ve d′
doğrularıdır.
|PD′| = 10 birim
|PF′| = 6 birim
|PL| = 5 birim
olduğuna göre |AK| = x kaç birimdir?
d
C
D x
E) 2
3
O merkezli, F ve F′
y
odaklı yandaki elipste
d doğrultmanlardan
P 15
biridir. P noktası
10
F'
elips üzerinde olup
O
F A
PFKD bir
dikdörtgendir.
|PF| = 10 birim
|PD| = 15 birim
olduğuna göre |FA| kaç birimdir?
B) 3
C) 12
F
5.
y
A) 4
3.
A) 2
B) 11
d
D
D) 5
B) 5
C) 6
D) 7
E) 8
6.
O merkezli
y
d
yandaki elipste, d'
P
F ve F′
D
odaklarına ait
4,8
doğrultmanlar
3 2 F'
O
F
x
sırasıyla d ve d′
doğrularıdır.
PD ⊥ d
Uzunluklar
şekilde verildiği gibiyse |PD| kaç birimdir?
d
D
K x
E) 6
A) 9
385
B) 10,8
C) 11
D) 12
E) 13