KUADRATİK FORMLAR

KUADRATİK FORMLAR
KUADRATİK FORM
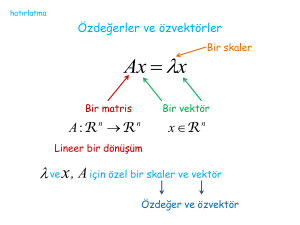
Tanım: Kuadratik Form
Bir q(x1,x2,…,xn) fonksiyonu qx : n   şeklinde tanımlı ve xixj bileşenlerinin
doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur. Bir kuadratik
form şu şekilde yazılabilir:
qx  xT Ax
Burada A, nn boyutlu eşsiz bir simetrik matristir. Aynı zamanda A, q karesel formunun
tanım matrisi olarak da adlandırılır.


Kuadratik formlar kümesi Qn  q  x1 , x2 ,..., xn  ,  n uzayından  uzayına tanımlı tüm
doğrusal fonksiyonların bir alt kümesidir.
KUADRATİK FORM
Örnek:
Aşağıdaki kuadratik form için A matrisini bulunuz.
q( x1 , x2 , x3 )  9 x12  7 x22  3x32  2 x1x2  4 x1x3  6 x2 x3
Çözüm:
aii  xi2 ‘lerin katsayısı
1
aij  a ji  ( xi x j ‘lerin katsayısı)
2
O halde,
 9 1 2 
A   1 7 3
 2 3 3 
KÖŞEGENLEŞTİRME
Teorem: Bir Kuadratik Formun Köşegenleştirilmesi
qx  xT Ax bir kuadratik form ve A, n×n boyutlu simetrik bir matris olsun.
 , A için ortanormal bir baz ve 1 , 2 ,..., n de ilgili özdeğerler olsun. O halde
c1
1 0
0 
2
cn  


0 0
0
 c1 

0  
 
 cn 
n 
q( x)  1c12  2c22  ...  ncn2
Burada ci ‘ler  ’ya göre x’in koordinatlarıdır.
KÖŞEGENLEŞTİRME
Örnek:
13x12  10 x1 x2  13x22  25 şeklinde tanımlanmış kuadratik formu ele alalım.
13x  10 x1 x2  13x   x1
2
1
2
2
13  
5
5
13  
13 5  x1 
x2  
  x  şeklinde matris notasyonunu kullanabiliriz.
5
13


 2
0
1  8 , 2  18
1
 1
1  8 için, özvektör v1    ; 2  18 için özvektör v2    ’dir. Bulunan bu
1
1
özvektörler ortogonaldir.
O halde bu kuadratik form şu şekilde yazılabilir:
8c12  18c22  25
Teorem: Herhangi bir gerçel A matrisi ve tüm gerçel x vektörleri için
xTAx=0 eşitliği ancak ve ancak A matrisi çarpık simetrik ise sağlanır.
Teorem: Eğer A ve B matrisleri simetrik ise tüm gerçel x vektörleri için xTAx= xTBx
eşitliği ancak ve ancak A=B ise sağlanır.
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
Aşağıdaki denklem üzerinden özdeğerleri ele alalım.
ax12  2hx1 x2  bx2 2  c
Burada a, h, b sıfırdan farklıdır. ax12  2hx1 x2  bx2 2 İfadesi x1 ve x2’ye göre
bir kuadratik form olarak adlandırılır. Bu eşitlik aynı zamanda şu şekilde
de gösterilebilir:
ax12  2hx1 x2  bx2 2   x1
 a h   x1 
T
x2  
x
Ax




 h b   x2 
 x1 
a h
Burada x    ve A  
’dir. A kuadratik formun tanım matrisi olarak

h b 
 x2 
adlandırılır.
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
Şimdi x1 ve x2 eksenlerini saat yönünün tersine θ kadar çevirerek yeni eksenler x1' ve x2'
elde edilsin. Eksenlerin dönüşümünü gösteren denklemler şu şekilde elde edilir:
Bir P matrisinin x1 ve x2 eksenine bağlı koordinatları (x1, x2), x1' ve x2' eksenine bağlı


'
'
koordinatları da x1 , x2 olsun. Aşağıdaki şekil göz önüne alınarak,
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
x2
x2'
x1'
x1
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
x1  OQ  OP cos(   )
 OP  cos  cos   sin  sin  
  OP cos   cos    OP sin   sin 
 OR cos  PR sin 
 x1' cos   x2' sin 
Not: cos( x  y)  cos x cos y  sin x sin y
Aynı şekilde,
x2  QP  OP sin(   )
 OP(sin  sin   cos cos  )
 (OP sin  )sin   (OP cos  ) cos 
x2  x1' sin   x2' cos 
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
Bu dönüşüm denklemleri matris formunda şu şekilde gösterilebilir:
 x1  cos 
 x    sin 
 2 
cos 
Burada P  
 sin 
 sin    x1' 
 
cos    x2' 
 sin  
T
PP
 I2
olmak
üzere,
P
matrisi
ortogonaldir.
Yani

cos  
dir. Ayrıca det(P)=1’dir. Bu özellikleri taşıyan matrislere “rotasyon matrisi” denir.
Ayrıca yeni koordinatları eski koordinatlar cinsinden elde etmek mümkündür.
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
 x1' 
cos 
T
 'YP x
 sin 
 x2 
 sin    x1 
cos    x2 
Böylece x1'  x1 cos   x2 sin  ve x2'   x1 sin   x2 cos  olur. O halde,
xT Ax   PY  A  PY   YT  PT AP  Y Olur.
T
Buradan anlaşılacağı gibi PT AP ’yi diag  1 , 2  gibi köşegen matris haline
getirecek herhangi bir θ açısı seçmek mümkündür.
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
x Ax   x
T
'
1

x   1
0
'
2
0   x1' 
' 2
' 2
x
x







1
1
2
2
2   x2' 
ax 2  2hxy  by 2  c Denklemi yeni eksenlere göre 1  x1'   2  x2'   c haline
2
2
dönüşmüştür. p1 ve p2 , P matrisinin sütunları olmak üzere aşağıdaki eşitlikler
sağlanmaktadır:
Ap1  1p1 ve Ap 2  2p 2
Bu denklemler 1 ve 2 üzerine bir takım kısıtlamalar getirmektedir. Örneğin,
u 
p1   1  olsun. İlk denklem,
 v1 
a
h

h  u1 
u1 
 a  1


ya
da
1 

 h
b   v1 
 v1 

 u1  0 

şekline dönüşür.
b  1   v1  0 
h
KUADRATİK FORMLAR VE DOĞRUSAL
DÖNÜŞÜMLER
İki bilinmeyenli, iki doğrusal denklemli bir homojen sistemle ilgilenildiği için,
a  1
h
h
b  1
0
Aynı şekilde 2 de bu eşitliği sağlamaktadır. Genişletilmiş formda bu ifade
 2   a  b    ab  h2  0 olur. Bu denklemin reel kökleri

ab
 a  b   4  ab  h2 
2
2

ab
a  b
2
 4h2
2
 2   a  b    ab  h2  0 denklemi, A matrisinin özdeğer denklemidir.
Yukarıdaki örnekte p1 ve p2 ,sırasıyla λ1 ve λ2’ye karşılık gelen özvektörlerdir.
TEMEL EKSENLER
Tanım: Temel Eksenler
qx  xT Ax bir kuadratik form, A ise n×n boyutlu ve n farklı
özdeğere sahip simetrik bir matris olsun. A’nın öz uzayları
(eigenspaces)’na q’nun temel eksenleri denir.
ELİPSLER VE HİPERBOLLER
Teorem: Elipsler ve Hiperboller
 2 ‘de tanımlı bir eğri olan C, şu şekilde tanımlanmıştır:
q( x1 , x2 )  ax12  bx1 x2  cx22  1
a b 
2
‘nın özdeğerleri 1 ve 2 olsun.
q’nun matrisi olan 
b
c 
 2

Eğer 1 ve 2 pozitifse C bir elips, biri pozitif diğeri negatifse C bir hiperboldür.
ELİPSLER VE HİPERBOLLER
1.durum: q( x1 , x2 )  ax12  bx1 x2  cx22  1 , b>a>0. Bu durumda eğri bir elipstir ve
eksenleri kestiği noktalar 1
a ve 1
b ’dir. O halde,
a   b 2 
 b 2 c  


1 a 
 0 
 x1 
  sin  

 x   cos  
 2
 0 
1 b 
2.durum: q( x1 , x2 )  ax12  bx1 x2  cx22  1 , a>0 ve b<0. Bu durumda eğrü hiperboldür.
 a   b 2 

c   
 b 2
ELİPSLER VE HİPERBOLLER
1.durum
2.durum
POZİTİF TANIMLI MATRİSLER
Tanım: Temel Alt Matrisler ve Pozitif Tanımlılık
A, nxn boyutlu simetrik bir matris olmak üzere; m  1,..., n için A( m ) de A’nın
m’ye kadar olan satır ve sütunlarının çıkarılmasıyla elde edilen mxm’lik bir matris
ise bu A( m ) matrislerine A’nın temel alt matrisleri denir.
A matrisi tüm m  1,..., n için det( A( m) )  0 koşulu sağlanıyorsa pozitif tanımlıdır.
POZİTİF TANIMLI MATRİSLER
Örnek:
 9 1 2 
A   1 7 3 matrisi pozitif tanımlı mıdır?
 2 3 3 
Çözüm:
det( A(1) )  det 9  9  0
 9 1
 62  0
det( A )  det 

 1 7 
(2)
det( A(3) )  det  A  89  0
Böylece A’nın pozitif tanımlı olduğunu söyleyebiliriz.
POZİTİF TANIMLI MATRİSLER
Tanım: Özdeğerler ve Pozitif Tanımlılık
Simetrik bir A matrisi sadece ve sadece tüm özdeğerleri pozitif olduğunda pozitif
tanımlıdır. Eğer özdeğerleri pozitif veya sıfırsa A matrisi yarı pozitif tanımlıdır.
Determinant, özdeğerlerden oluştuğu için pozitif tanımlı bir matrisin determinantı da
pozitiftir. Fakat tersi durum geçerli değildir.
POZİTİF TANIMLI MATRİSLER
Özdeğerlerinden biri pozitif ve diğer ikisi negatif olan 3×3 boyutlu bir A matrisini
ele alalım. det(A) pozitiftir fakat qx  xT Ax pozitif tanımlı değildir.
A matrisi nn boyutlu simetrik bir matris ve x vektörü n elemanlı bir sütun
vektörü ise karesel formun genel yapısı,
xT Ax  a11 x12  2a12 x1 x2  2a13 x1 x3 
 2a1n x1 xn
 a22 x22  2a23 x2 x3    2a2n x2 xn
 a33 x32    2a3n x3 xn

  a nn x n2
ifadesi ile verilebilir.
POZİTİF TANIMLI MATRİSLER
Tanım: Bir Kuadratik Formun Tanımlılığı
qx  xT Ax bir kuadratik form ve A, n×n boyutlu simetrik bir matris olsun.
Eğer  n ‘de x’in tüm sıfır olmayan değerleri için q( x) pozitifse A pozitif tanımlı,
q( x)  0 ise A pozitif yarı tanımlıdır.
Eğer q hem pozitif hem de negatif değerler alabiliyorsa A belirsiz (indefinite)’dir.
POZİTİF TANIMLI MATRİSLER
Tüm x≠0 sütun vektörleri için eğer xTAx>0 ise karesel form ve A matrisi
pozitif tanımlıdır. Eğer tüm x≠0 sütun vektörleri için xTAx0 ise karesel
form ve matris pozitif yarı tanımlıdır. Yukarıdaki eşitsizliklerin yönü
değiştirilerek negatif tanımlı ve negatif yarı tanımlı karesel form ve matrisler
tanımlanabilir. Eğer bir form bazı x vektörleri için pozitif, diğerleri için negatif
ise tanımsızdır.