bilişim teknolojileri için işletme istatistiği - SABİS

SAKARYAÜNİVERSİTESİ
BİLİŞİMTEKNOLOJİLERİ
İÇİNİŞLETME
İSTATİSTİĞİ
Hafta10
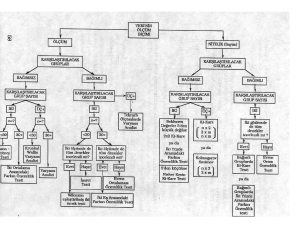
Yrd. Doç. Dr. Halil İbrahim CEBECİ Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi’ne aittir. "Uzaktan Öğretim" tekniğine uygun olarak hazırlanan bu ders içeriğinin bütün hakları saklıdır. İlgili kuruluştan izin almadan ders içeriğinin tümü ya da bölümleri mekanik, elektronik, fotokopi, manyetik kayıt veya başka şekillerde çoğaltılamaz, basılamaz ve dağıtılamaz. 0 Her hakkı saklıdır © 2013 Sakarya Üniversitesi BÖLÜM 5 ÇIKARIMSAL İSTATİSTİK BÖLÜMÜN AMACI Bu bölümün amacı en önemli istatistiksel dağılım olan normal dağılım ile ilgili temel bilgileri öğrenmek, normal olasılıkların hesaplanıp yorumlanmasını kavrayabilmektir. 5.3. Çift Örneklem Testleri İki farklı örneklemin birbiri ile arasındaki farklılıkların istatistiksel açıdan anlamlı olup olmadığının analiz edilmesi için çift örneklem testleri kullanılır. Veri analizleri için kullanılacak testler verilerin bağımsız veya eşleştirilmiş olması ve verilerin normal dağılıma uyup uymaması ile birlikte farklılık gösterilir. 1 Tek Örneklem
Parametrik Veri
Tek Örneklem T Testi
Parametrik Olmayan Veri
Wilcoxon İşaretli Sıralar testi Parametrik Veri
Bağımsız Örneklem T‐Testi
Parametrik Olmayan Veri
Mann Whitney U Testi
Parametrik Veri
Eşleştirilmiş Örneklem T Testi
Parametrik Olmayan Veri
Wilcoxon
Eşleştirilmiş Çiftler Testi
Bağımsız Veri
Bağımsız Veri
Çift Örneklem
Karşılaştırmalı Veri Analizi
Eşleştirilmiş Veri
Tek Faktör (ANOVA)
Parametrik Veri
Varyans Analizi
Çift Faktör
Parametrik Olmayan Veri
Kruskal Wallis Testi
Çok Faktör (MANOVA)
Parametrik Veri
Rastgele Blok Dizaynı
Parametrik Olmayan Veri
Friedman Testi
Bağımsız Veri
İkiden Fazla Örneklem
Bağımlı Veri
5.3.1. Bağımsız Örneklem T‐Testi Eğer verilerin arasında ilişki yoksa (Veriler Bağımsız ise) ve veriler normal dağılıyorsa o zaman “Bağımsız Örneklem T‐Testi” hipotezlerin doğruluğunun araştırılması için kullanılır. Bu analizin nasıl kullanıldığını önceki derste vermiş olduğumuz “Öğrenci boyları” ile ilgili örneğin verilerini kullanarak açıklayalım. ÖRNEK Bir araştırmacı Sakarya Üniversitesi Beden Eğitimi Yüksek Okulu (BESYO) Öğrencilerinin diğer bölüm
öğrencilerinden farklı boy ortalamasına sahip olduklarını düşünmektedir. Aşağıda BESYO ve Merkez kantinde rastgele seçilen 15 öğrenci boyları verilmiştir. Acaba gerçekten BESYO öğrencilerinin boy ortalaması farklı mıdır? (Veriler normal dağılmaktadır) (BESYO öğrencileri sadece BESYO kantinini kullanırken, diğer bölümler için bu kantini kullanmak mümkün değildir) 2 MERKEZ KANTİN BESYO KANTİNİ 175 169 175 177 180 197 187 193 187 172 168 183 178 175 193 183 167 190 191 192 179 186 180 171 196 170 164 188 178 175 ÇÖZÜM Öncelikle araştırma hipotezleri belirlenmelidir. Boy ortalamaların farklılığı öngörülmesine rağmen,
farklılığın hangi yönde olduğu belirtilmemiştir. Bu bağlamda Çift yönlü hipotez testi kullanılması
uygundur. :Ü
:
üü öü
ğ öü
. . Uygun test yöntemi ve anlamlılık düzeylerinin belirlenmesi bu sorunun ikinci adımıdır. İki farklı grubun analizi yapıldığı, verilerin normal dağıldığı soruda verildiğinden ve örneklemlerin bağımsız
olduğu da dikkate alındığında “Bağımsız Örneklem T‐Testi” yöntemini 0,05 değerinde test etmeyi tercih ediyoruz. Daha sonra analizler Excel yardımıyla gerçekleştirilebilir. EXCEL Öncelikle elimizde bulunan verileri analize uygun şekilde Excel’e yerleştirmeliyiz. 3 Veri yukarıdaki gibi girildikten sonra Veri Çözümleme aracına gidilerek, “T‐Test: Farklı Varyanslar Varsayarak İki Örnek” testi seçilir. (Farklı paket programlarda eşit varyanslık durumu öncelikle
incelenebilir) Aşağıdaki ekranda ilgili yerler girilir. Resim şu anda görüntülenemiy or.
Gelen ekranda “Değişken 1 Aralığı” alanına test için girdiğimiz “MERKEZ KANTİN” ve “Değişken 2
Aralığı” alanına ise “BESYO KANTİNİ” sütunu değerleri seçilir. Eğer veri seçimlerinde açıklama
satırları seçildi ise (Bu soruda seçilmiştir), o zaman “Etiketler” kutucuğu seçilmelidir. Son olarak “Alfa”
kutucuğuna anlamlılık düzeyi değeri girilmelidir. Bu işlemler bittikten sonra analiz sonuçlarını istediğimiz alan “Çıkış Aralığı” kısmından seçilmelidir. 4 Yukarıdaki analiz sonuç tablosu incelendiğinde kabul olasılığı değerinin anlamlılık seviyesi değerinden
(ki biz bu soruda 0,05 olarak seçmiştik) daha yüksek olduğu görülmektedir. Bu durumda Red bölgesinde yer almayan olasılık değeri sonucu dikkate alınarak İki boy ortalamasının eşitliğini
öngören sıfır hipotezi kabul edilecektir. Yani BESYO bölümü boy ortalamasının (182,267 cm), okulun
diğer kısımlarının boy ortalamasından (176,933) farklı olduğu tezi uygun değildir. Analizi yorumlarken diğer bölümleri sadece 15 kişi ile değerlendirmek uygun olmayabilir. Eğer bütün
okulun ortalamasını biliyorsak bu durumda tek örneklem t testi kullanarak, bu ortalamadan
farklılıklar test edilebilir. 5.3.2. Mann Whitney U Testi Eğer veriler bağımsız olmasına karşın, dağılımı hakkında bir bilgi mevcut değilse, veya normal dağılmadığı öngörülüyorsa o zaman Bağımsız Örnek T Testi yerine Mann Whitney U Testi kullanılmalıdır. ÖRNEK Bir araştırmacı Sakarya Üniversitesi Beden Eğitimi Yüksek Okulu (BESYO) Öğrencilerinin diğer bölüm
öğrencilerinden farklı boy ortalamasına sahip olduklarını düşünmektedir. Aşağıda BESYO ve Merkez
kantinde rastgele seçilen 15 öğrenci boyları verilmiştir. Acaba gerçekten BESYO öğrencilerinin boy ortalaması farklı mıdır? (Veriler normal dağılmamaktadır) (BESYO öğrencileri sadece BESYO kantinini kullanırken, diğer bölümler için bu kantini kullanmak mümkün değildir) MERKEZ KANTİN BESYO KANTİNİ 175 169 175 177 180 197 187 193 187 172 168 183 178 175 193 183 167 190 191 192 179 186 180 171 196 170 164 188 178 175 5 ÇÖZÜM Araştırma hipotezleri önceki soru ile aynıdır. :Ü
:
üü öü
ğ öü
. . Fakat verilerin normal dağılmadığı öngörüldüğü için Bağımsız Örneklem T Testi kullanılamayacaktır. Bu bağlamda Mann Whitney U Test istatistiği hesaplanmalıdır. Parametrik olmayan bu testi Excel ile
yapmak mümkün değildir. Farklı paket programlar yardımıyla aşağıdaki gibi bir sonuç tablosu elde
edilebilir. Parametreler Değerler Sıraların Ortalaması Grup 1 13,13 Sıraların Ortalaması Grup 2 17,87 Test Değeri (Z) ‐1,475 Kabul Olasılığı ( ) 0,140 Yukarıdaki tablodan da görüleceği üzere Mann Whitney U testi de, bağımsız örneklem t testi benzeri
sonuç üretmiştir. Kabul olasılığının anlamlılık düzeyinden yüksek olması eşitlik durumunu öngören
sıfır hipotezinin kabulü durumunu ortaya çıkarmıştır. Bu durumda önceki sorudaki yorumla tutarlı
olarak bu iki grup birbiri ile istatistiksel olarak herhangi bir farklılık göstermemektedir. 5.3.3. Eşleştirilmiş Örneklem T‐Testi Bu testte önceki anlatılan iki testten farklı olarak bağımsızlık varsayımı söz konusu değildir. Burada veriler tek bir grubun iki farklı durumunun karşılaştırılması şeklindedir. Yani bir deneyin iki sonucu, bir ilacın alınmadan ve alındığı durumların karşılaştırılması gibi eşli veri setleri söz konusu olduğunda eşleştirilmiş örneklem t testi tercih edilir. Bu test için de verilerin normal dağıldığı varsayımı söz konusudur. DİKKAT Bağımsız örneklem testlerinde iki farklı grubun aynı zamandaki durumları dikkate alınırken,
eşleştirilmiş örneklem testlerinde bir grubun iki farklı zamandaki durumları dikkate alınır. ÖRNEK 6 Bir ayakkabı firması özel tabanlı, fiber malzemeden üretilmiş yeni bir ayakkabı üretmiştir. Firma yetkilileri bu ayakkabı ile insanlarına aynı sürede daha fazla mesafe gidebileceklerini öngörmektedir.
Bu durumu da bağımsız bir araştırma şirketine test ettirmektedir. Araştırma şirketi firmanın bir önceki ayakkabı modelini kullanan 15 kişiyi belirli bir parkurda, benzer hava koşullarında 60 dakika
boyunca yürütmüş ve gidilen mesafeleri not etmiştir. Daha sonra yine benzer hava koşullarından,
aynı dinlenme düzeyinde, aynı 15 kişiye yeni dizayn edilen ayakkabı giydirilerek tekrar aynı parkurda
yürütülmüş ve gidilen mesafelere not edilmiştir. Bu araştırma şirketinin elde ettiği verilere
aşağıdadır. Acaba ayakkabı gerçekten de daha fazla mesafe gidilmesini sağlıyor mudur? (Veriler normal dağılmaktadır.) ÇÖZÜM Öncelikle yine araştırma hipotezleri belirlenmelidir. :
ö
ü ü
:
ö
ü ü
. . Uygun test yöntemi ve anlamlılık düzeylerinin belirlenmesi bu sorunun ikinci adımıdır. İki farklı
grubun analizi yapıldığı, verilerin normal dağıldığı soruda verildiğinden ve örneklemlerin eşleştirilmiş
olduğu da dikkate alındığında “Eşleştirilmiş Örneklem T‐Testi” yöntemini 0,05 değerinde test etmeyi tercih ediyoruz. Excel yardımıyla eşleştirilmiş örneklem t testi çözümü aşağıda verilmiştir. 7 EXCEL Veri Çözümleme aracına gidilerek, “T‐Test: Ortalamalar İçin İki Örnek” testi seçilir. Aşağıdaki ekranda
ilgili yerler girilir. Gelen ekranda “Değişken 1 Aralığı” alanına test için girdiğimiz “Önceki Model” ve “Değişken 2 Aralığı” alanına ise “Yeni Model” sütunu değerleri seçilir. Eğer veri seçimlerinde açıklama satırları
seçildi ise (Bu soruda seçilmiştir), o zaman “Etiketler” kutucuğu seçilmelidir. Son olarak “Alfa”
kutucuğuna anlamlılık düzeyi değeri girilmelidir. Bu işlemler bittikten sonra analiz sonuçlarını istediğimiz alan “Çıkış Aralığı” kısmından seçilmelidir. 8 Yukarıdaki analiz sonuç tablosu incelendiğinde kabul olasılığı değerinin anlamlılık seviyesi değerinden
(ki biz bu soruda 0,05 olarak seçmiştik) daha düşük olduğu görülmektedir. Bu durumda Red bölgesinde yer alan olasılık değeri sonucu dikkate alınarak İki boy ortalamasının eşitliğini öngören
sıfır hipotezi kabul edilmeyecektir. Yani önceki modelle gidilen ortalama yürüme mesafesi (19807),
yeni modelle gidilen ortalama mesafeden (20011,93) den istatistiksel açıdan farklıdır. Yani yeni
modelle gerçekten de daha uzun mesafe gitmek mümkündür. 5.3.4. Wilcoxon Eşleştirilmiş Çiftler Testi Önceki anlattığımız test olan eşleştirilmiş örneklem t testi yönteminden farklı olarak Wilcoxon Eşleştirilmiş Çiftler testinde verilerin normal dağıldığı varsayımı aranmaz. Bu testte de eşleştirilmiş veri seti zorunluluğu vardır. ÖRNEK Önceki örnekte vermiş olduğumuz ayakkabı örneğindeki verilerin normal dağılmadığı varsayıldığı durumda hangi analiz yapılmalıdır. Yorumlayınız. ÇÖZÜM 9 Sorunun hipotezleri değişmez. Fakat parametrik olmayan veri seti olduğundan, Wilcoxon Eşleştirilmiş Çiftler Testi kullanılmalıdır. Anlamlılık düzeyi diğer testteki sonuçlarla karşılaştırılması amacı ile yine 0,05 olarak alınacaktır. Parametrik olmayan bir test olan Wilcoxon Eşleştirilmiş Çiftler Testinin Excel veri çözümleme
yardımıyla çözülmesi mümkün değildir. Bu bağlamda sorunun sonucu diğer paket programların bir
benzeri olarak aşağıdaki gibi sunulmuştur. Parametreler Değerler Negatif Sıralar (Yeni Model < Önceki 13,13 Model) Pozitif Sıralar (Yeni Model > Önceki Model)
17,87 Test Değeri (Z) ‐3,011 Kabul Olasılığı ( ) 0,003 Yukarıdaki sonuç tablosundan da görüleceği üzere sıfır hipotezi red edilerek (Çünkü kabul olasılığı
anlamlılık düzeyinin altında) iki model ile yürünen mesafelerin farkının öngörüldüğü alternatif
hipotez kabul edilmiştir. ÖZET Çift örneklem testlerinin en önemlileri, Bağımsız Örneklem T testi, Mann Whitney U testi,
Eşleştirilmiş Örneklem t testi ve Wilcoxon Eşleştirilmiş Çiftler testi şeklindedir. Eğer veriler bağımsız ise yani iki farklı grubun aynı zamandaki durumlarını betimliyorsa, o zaman, normal dağılma varsayımına uyan veri setleri için bağımsız örneklem t testini, normal dağılıma
uymayan veri setleri için Mann Whitney U testini, iki grubun ortalamalarını farklılıklarını araştırmak
için kullanılır. Veriler eşleştirilmiş ise, yani bir grubun iki farklı zaman aralığındaki değerleri mevcutsa, istatistiksel
olarak bu iki durumun farklı olup olmadığı araştırılırken, parametrik testlerde eşleştirilmiş örneklem t
testi ve parametrik olmayan testlerden Wilcoxon Eşleştirilmiş Çiftler testi kullanılır. SON NOT 1. Verilerin bağımsız olup olmadıkları çok büyük önem arz etmektedir. Bu yüzden veri seti iyi
anlaşılmadan analiz yöntemi seçilmesi tercih edilmemelidir. 10 2. Normal dağılıma uyup uymadığı bilinmeyen bir veri seti eğer normal dağılan bir ana kütleden çekildiği bilgisi mevcut ise parametrik testlerle değerlendirilebilir. 3. Bazı paket programlar tek yönlü hipotez testleri için kabul olasılıklarını vermez, bu
durumlarda çift yönlü verilen test istatistiğinin ikiye bölünmesi pratik bir yol olarak tercih edilebilir. 4. Anlatılan analizlerin sadece sayısal (sayılabilir, aralık) verilerinde yapıldığına dikkat ediniz. ÇALIŞMA SORULARI S1 – Mühendislik Fakültesi ve İşletme Fakültesi öğrencilerinin ALES puanları üzerine yapılan
çalışmada yer iki fakültede sınava giren 20 şer öğrenci seçilmiştir? İşleme Öğrencileri Mühendislik Öğrencileri
1 81 1 90 2 76 2 88 3 78 3 86 4 69 4 78 5 79 5 71 6 80 6 79 7 83 7 82 8 88 8 78 9 77 9 88 10 78 10 96 11 82 11 78 12 60 12 72 13 91 13 69 14 87 14 89 15 80 15 86 16 67 16 83 17 77 17 87 18 78 18 92 11 19 82 19 97 20 80 20 91 1.
Verilerin normal dağıldığı varsayıldığında acaba bu fakülte öğrencilerinin ortalama ALES puanları arasında bir farklık var mıdır? 2.
Verilerin normal dağılmadığı durumda a şıkkını tekrar analiz ediniz. S2 – Bir araştırma şirketi piyasaya sürülen bir otomobil yağ katkı maddesinin, yağ ömrünü artırıp
artırmadığını incelemek istemektedir. Bu amaçla 10 arabaya yağ katkı maddesi koymadan 10000
kilometre kullanılmış ve yağ miktarı ölçülmüştür. Daha sonra aynı 10 arabaya katkı maddesi aynı
miktar yağa karıştırılarak 10000 kilometre gitmesi sağlanıp ölçümler gerçekleştirilmiştir. Ölçümler aşağıdadır. Katkı Maddeli Yağ Katkı Maddeli Yağ 1 1,35 1 1,39 2 1,32 2 1,35 3 1,27 3 1,41 4 1,41 4 1,51 5 1,37 5 1,39 6 1,39 6 1,48 7 1,27 7 1,33 8 1,22 8 1,27 9 1,49 9 1,52 10 1,39 20 1,39 1.
Verilerin normal dağıldığı varsayıldığında acaba katkı maddesi yağ koruma konusunda faydalı
mıdır? 2.
Verilerin normal dağılmadığı durumda a şıkkını tekrar analiz ediniz. KAYNAKLAR 1. Keller, Gerald; Statistics for Management and Economics, 9e, 2012 2. McClave, J.T, Benson, P.G, Sincich, T.; Statistics for Business and Economics, 11e, 2011 3. Sharpe N.R., De Veaux R.D., Velleman P.F.; Business Statistics 2e, 2012 12 13