Behcet DAĞHAN DİNAMİK Dersi FİNAL Sınavı Soruları ve

S.Ü. Mühendislik Fakültesi
Makina Mühendisliği Bölümü
10 Ocak 2013
DİNAMİK Dersi FİNAL Sınavı Soruları ve Çözümleri
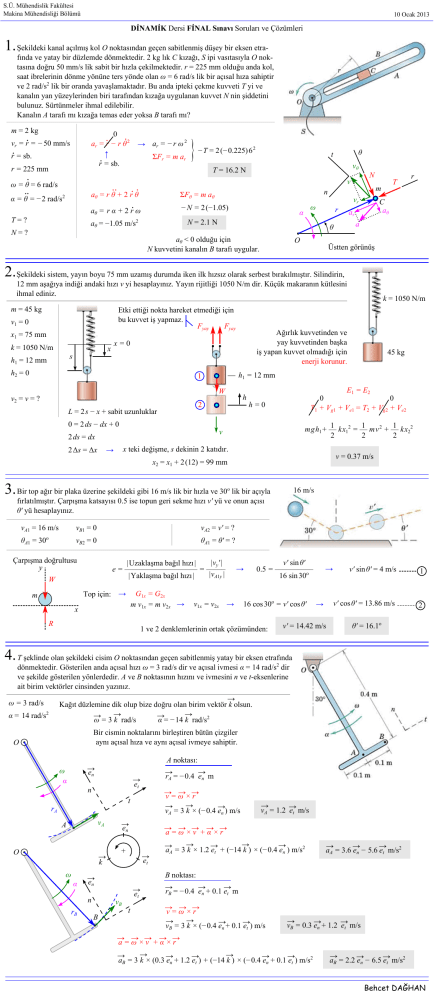
1. Şekildeki kanal açılmış kol O noktasından geçen sabitlenmiş düşey bir eksen etra-
fında ve yatay bir düzlemde dönmektedir. 2 kg lık C kızağı, S ipi vasıtasıyla O noktasına doğru 50 mm/s lik sabit bir hızla çekilmektedir. r = 225 mm olduğu anda kol,
saat ibrelerinin dönme yönüne ters yönde olan ω = 6 rad/s lik bir açısal hıza sahiptir
ve 2 rad/s2 lik bir oranda yavaşlamaktadır. Bu anda ipteki çekme kuvveti T yi ve
kanalın yan yüzeylerinden biri tarafından kızağa uygulanan kuvvet N nin şiddetini
bulunuz. Sürtünmeler ihmal edilebilir.
Kanalın A tarafı mı kızağa temas eder yoksa B tarafı mı?
m = 2 kg
0
ar = r − r θ 2
→ ar = − r ω 2
→
vr = r = − 50 mm/s
r = sb.
ΣFr = m ar
r = sb.
r = 225 mm
}
− T = 2 (− 0.225) 6 2
θ
t
vθ
T = 16.2 N
v
ω = θ = 6 rad/s
α = θ = − 2 rad/s
2
T=?
N=?
n
aθ = r θ + 2 r θ
ΣFθ = m aθ
aθ = r α + 2 r ω
− N = 2 (−1.05)
aθ = −1.05 m/s2
N = 2.1 N
r
O
r
C
aθ
ar
a
θ
aθ < 0 olduğu için
N kuvvetini kanalın B tarafı uygular.
T
m
vr
ω
α
N
Üstten görünüş
2.Şekildeki sistem, yayın boyu 75 mm uzamış durumda iken ilk hızsız olarak serbest bırakılmıştır. Silindirin,
12 mm aşağıya indiği andaki hızı v yi hesaplayınız. Yayın rijitliği 1050 N/m dir. Küçük makaranın kütlesini
ihmal ediniz.
m = 45 kg
Etki ettiği nokta hareket etmediği için
bu kuvvet iş yapmaz.
Fyay
Fyay
v1 = 0
x1 = 75 mm
k = 1050 N/m
s
h1 = 12 mm
Ağırlık kuvvetinden ve
yay kuvvetinden başka
iş yapan kuvvet olmadığı için
enerji korunur.
x=0
x
h2 = 0
W
0 = 2 ds − dx + 0
E1 = E 2
0
0
T1 + Vg1 + Ve1 = T2 + Vg2 + Ve2
h=0
1
1
1
mgh1+ –– kx12 = –– mv 2 + –– kx22
2
2
2
v
2 ds = dx
x teki değişme, s dekinin 2 katıdır.
→
2 Δs = Δx
h
2
L = 2 s − x + sabit uzunluklar
45 kg
h1 = 12 mm
1
v2 = v = ?
k = 1050 N/m
v = 0.37 m/s
x2 = x1 + 2 (12) = 99 mm
3. Bir top ağır bir plaka üzerine şekildeki gibi 16 m/s lik bir hızla ve 30 lik bir açıyla
16 m/s
o
fırlatılmıştır. Çarpışma katsayısı 0.5 ise topun geri sekme hızı v' yü ve onun açısı
θ' yü hesaplayınız.
vA1 = 16 m/s
θA1 = 30
o
vB1 = 0
vA2 = v' = ?
vB2 = 0
θA1 = θ' = ?
Çarpışma doğrultusu
y
|vy' |
| Uzaklaşma bağıl hızı |
e = ––––––––––––––––––– = –––––
|vA1y |
| Yaklaşma bağıl hızı |
W
G1x = G2x
m v1x = m v2x →
Top için: →
m
x
R
→
v1x = v2x →
v' sin θ'
0.5 = ––––––––––
16 sin 30o
16 cos 30o = v' cos θ'
1 ve 2 denklemlerinin ortak çözümünden:
→
→
v' = 14.42 m/s
v' sin θ' = 4 m/s
1
v' cos θ' = 13.86 m/s
2
θ' = 16.1o
4. T şeklinde olan şekildeki cisim O noktasından geçen sabitlenmiş yatay bir eksen etrafında
dönmektedir. Gösterilen anda açısal hızı ω = 3 rad/s dir ve açısal ivmesi α = 14 rad/s2 dir
ve şekilde gösterilen yönlerdedir. A ve B noktasının hızını ve ivmesini n ve t-eksenlerine
ait birim vektörler cinsinden yazınız.
→
Kağıt düzlemine dik olup bize doğru olan birim vektör k olsun.
→
→
→
→
ω = 3 k rad/s
α = − 14 k rad/s2
ω = 3 rad/s
α = 14 rad/s2
Bir cismin noktalarını birleştiren bütün çizgiler
aynı açısal hıza ve aynı açısal ivmeye sahiptir.
O
A noktası:
→
en
ω
α
→
→
rA = − 0.4 en m
→
et
n
→ → →
v=ω×r
→
→
→
vA = 3 k × (− 0.4 en ) m/s
t
rA
vA
A
O
→
k
ω
α
→
et
→
→
→
→
→
aA = 3 k × 1.2 et + (−14 k ) × (− 0.4 en ) m/s2
→
→
→
aA = 3.6 en − 5.6 et m/s2
B noktası:
vB
B
→ → → → →
a=ω×v +α×r
+
→
en
n
rB
→
en
→
→
vA = 1.2 et m/s
→
et
t
→
→
→
rB = − 0.4 en + 0.1 et m
→ → →
v=ω×r
→
→
→
→
vB = 3 k × (− 0.4 en + 0.1 et ) m/s
→
→
→
vB = 0.3 en + 1.2 et m/s
→ → → → →
a=ω×v +α×r
→
→
→
→
→
→
→
aB = 3 k × (0.3 en + 1.2 et ) + (−14 k ) × (− 0.4 en + 0.1 et ) m/s2
→
→
→
aB = 2.2 en − 6.5 et m/s2
Behcet DAĞHAN