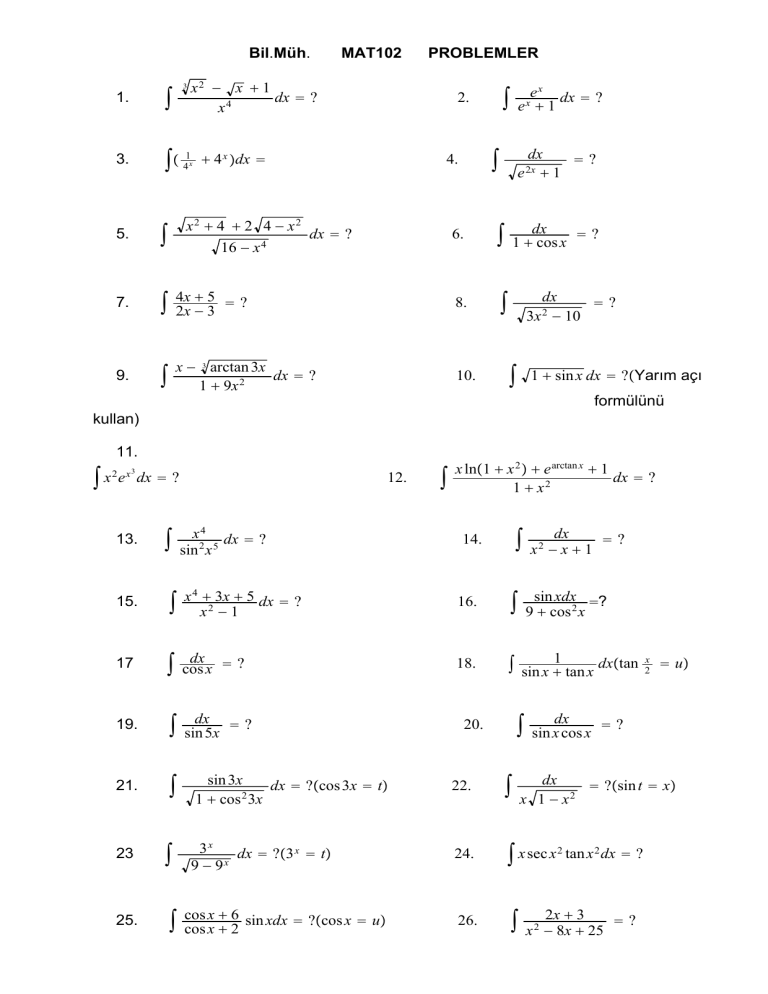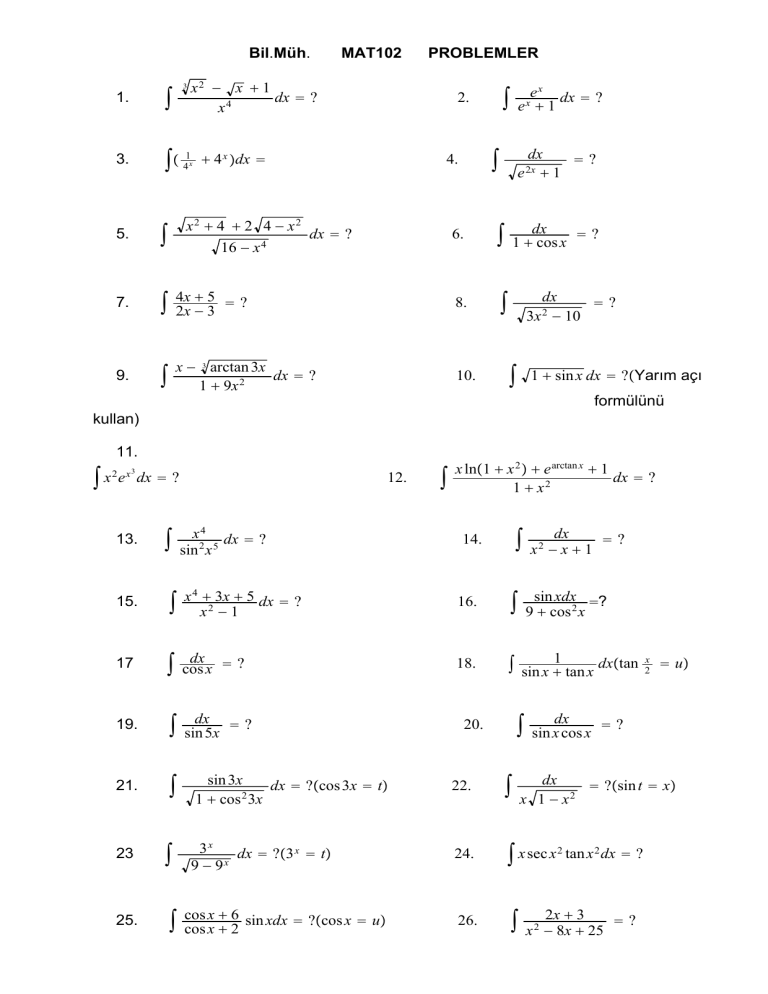
Bil.Müh.
MAT102
PROBLEMLER
x2 − x 1
dx ?
x4
1.
3.
41
5.
7.
9.
3
x
4 x dx
x2 4 2 4 − x2
2.
4.
dx
?
e 1
2x
6.
4x 5 ?
2x − 3
8.
x − 3 arctan 3x
dx ?
1 9x 2
10.
16 − x
4
dx ?
e x dx ?
e 1
x
dx
?
1 cos x
dx
?
3x − 10
2
1 sin x dx ?Yarım açı
formülünü
kullan)
11.
x 2 e x dx ?
3
12.
x ln1 x 2 e arctan x 1
dx ?
1 x2
13.
x 4 dx ?
sin 2 x 5
15.
x 4 3x 5 dx ?
x2 − 1
16.
sin xdx ?
9 cos 2 x
17
dx
cos x ?
18.
1
dxtan
sin x tan x
19.
dx ?
sin 5x
21.
sin 3x
dx ?cos 3x t
1 cos 2 3x
22.
23
3x
dx ?3 x t
x
9−9
24.
x sec x 2 tan x 2 dx ?
25.
26.
cos x 6 sin xdx ?cos x u
cos x 2
14.
20.
dx
?
x2 − x 1
x
2
u
dx
?
sin x cos x
dx
?sin t x
x 1 − x2
2x 3
?
x − 8x 25
2
27.
x
?
−x 2x 2
2
Kısmi İntegrasyon
udv uv − vdu
28.
x sin 3xdx ?
29.
30.
x 2 2x 5 cos 2xdx ?
31.
A e ax cos bxdx ?
sin 2 x
ex
dx ?
2x 1e −x dx ?
32.
Trigonometrik İntegraller
33.
x n ln xdx ?
34.
sin 2 xdx ?
35.
cos 2 3xdx ?
36.
cos 4 xdx ?
37.
sin 5 x cos 5 xdx ?
38.
sin 5 x cos 4 xdx ?
40.
sin 2 x cos 2 xdx ?
sin 6x cos 4xdx ?
39.
sin 3 xdx ?
41.
Trigonometrik Dönüşümler
42.
x 2 −25
x
44.
x2
46.
48.
9−x 2
1
x2
4−x 2
dx ?
dx ?
dx ?
1
x 2 −6x10
dx ?
43.
45.
1
x 2 −25
dx ?
dx ?
1
5−4x−2x 2
47.
49.
x2
5x 2
dx ?
x
x 2 6x10
dx ?
Basit Kesirlere Ayırarak İntegral Alma
50.
.
x2
dx ?
x2 x − 2
51.
2
x4 − x 2 dx ?
x − 5x 4
3x 5
dx ?
3
x − x2 − x 1
52.
54.
3
2
x 2 x 2x 2 dx ?
2
− 1 dx ?
x3 3x
2
53.
x 1x 2
x x − 2x
55.
2
x 2 3x − 4 dx ?
x − 2x − 8
56.
17 dx ?
11x
2
2x 7x − 4
57.
2
x − 4 dx ?
58.
x3
dx ?
x2 − x − 6
59.
3dx
x−1
x x
?
Genelleştirilmiş İntegraller
60.
e dx ?
−x
61.
0
62.
1
2
−
64.
4
0
1
1x 2
dx?
63.
?
65.
dx
x−1 2
İntegralin Uygulamaları
−4
ve
66.
y 1x
2
y 2 − x2
dx
x3
?
1
2
0 2x−1 3
4
3
dz
x−3 2
dx ?
?
eğrileri tarafından sınırlanan A alanını
bulunuz.
67.
y x2 1
68.
y
bulunuz.
69.
y
a.)
b)
70.
y
ve
2−x
ve
yx
eğrileri tarafından sınırlanan A alanını bulunuz.
y −x
eğrileri tarafından sınırlanan A alanını
x2
ve
y 4x
eğrileri tarafından sınırlanan A alanın
x e göre ıntegre ederek
y ye göre integre ederek bulunuz.
x 2 ve . x y 2
parabollerinin sınırladığı alanın x ve y eksenleri etrafında
döndürülmesiyle meydana gelen dönel yüzeylerin hacimlerini ve alanlarını
hesaplayınız.
71. Verilen eğrilerin uzunluklarını belirtilen aralıklarda bulunuz.
a.)
b.)
y 3x 2 −1
x 0, x 1
y lncosx
x 4 , x
c.)
x
3
1
8
y4
1
4
y −2
3
y 1, y 4
72.
Eğrilerin verileneksen etrafında verilen aralıkta döndürülmesiyle
oluşan yüzeyleri nalanlarını hesaplayınız.
−1 ≤ x ≤ 1
x − ekseni
a.)
4 − x2
b.)
2 1−y
−1 ≤ y ≤ 0
y − ekseni