Ünite 3 ISI

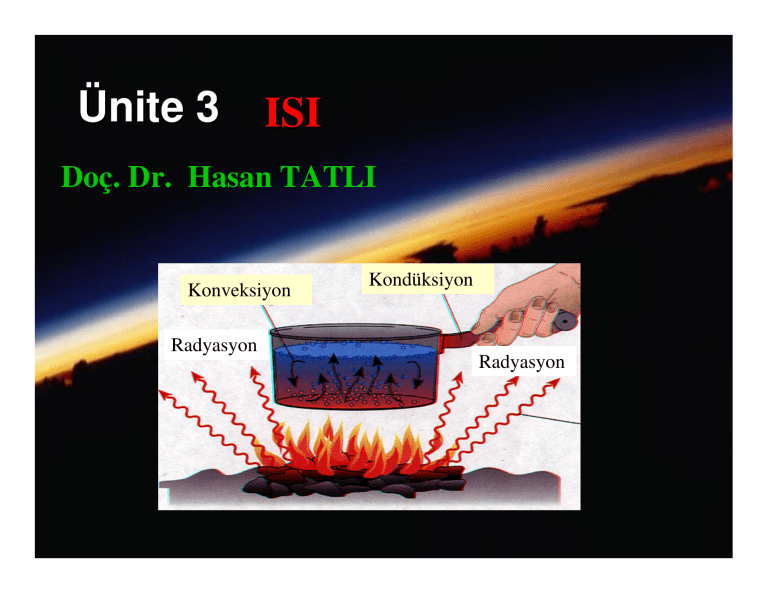
Ünite 3
ISI
Doç. Dr. Hasan TATLI
Konveksiyon
Radyasyon
Kondüksiyon
Radyasyon
64
ENERJİ NE YARATILABİLİR
NE DE YOK EDİLEBİLİR!
(Temel Fizik Yasa: Kütlenin Korumu Prensibi)
• Isı enerjinin bir şeklidir. Isının dünyaya girişinin ilk
adımı, kısa-dalga boylu güneş radyasyonu ile atmosfere
girmesidir.
• Atmosfere giren enerji hava olaylarını yönetimi
esnasında çok defa şekil değiştirir.
• En son adımda ise uzun-dalgalı (karasal radyasyon)
radyasyon şekline dönüşerek dünyayı terk eder.
65
HİSSEDİLEN ISI ve GİZLİ ISI
• Hissedilen Isı ∆QH ile gösterilir birimi Joule dür.
İnsanlar tarafından his edilir, yani sıcaklık farkını ortaya
çıkaran ısı miktarı olarak da tanımlanabilir.
∆QH = mhava Cp ∆T
Cp: sabit basınçta özgül ısı. Isıtılan maddenin bir
özelliğidir.
Kuru havanın özgül ısısı Cpd = 1004.67 J.kg-1 .K-1
Pratikte Cpd = 1005 alınabilir.
Csu = 4200 J kg-1K-1
Nemli hava için Cp = Cpd (1 + 0.84 . r)
r : karışma oranı birimi gsubuharı /gkuruhava dır.
66
Soru: 2 kg havanın sıcaklığını 5oC artırmak için ne kadar
hissedilen ısı gerekir?
Çözüm:
Verilenler: mhava = 2 kg; ∆T = 5oC
İstenen: ∆QH = ? J
∆QH = mhava Cp ∆T = (2 kg) (1004.67 J kg-1K-1)(5oC)
= 10.046 kJ (kilo Joule)
Kontrol: Birimler tamam. Fizik anlamlı.
Tartışma: Bu kadar hava yaklaşık 2.45 m3 hacme sahiptir – küçük
bir küvet kadardır.
67
Gizli Isı: Gizlenmiş veya depo edilmiş ısı enerjisidir,
sadece suyun faz değişimi esnasında ortaya çıkar.
Buharlaşma esnasında her buharlaşan su
damlacığı çevresinden hissedilen ısı enerjiyi
depolayarak gizler havayı soğutur.
Havayı soğutan faz değişimleri
i) Buharlaşma: sıvı su buharı
ii) Erime: katı (buz) sıvı
iii) süblimleşme: katı su buharı
68
Havayı ısıtan faz değişimleri
Yoğunlaşma su buharı sıvı
Donma: sıvı katı (buz)
Depozisyon: su buharı katı
Faz değişim ısı miktarı: ∆QE = msu . L
L = gizli ısı
69
L değerleri
Lv = +- 2.5 x 106J.kg-1 = yoğunlaşma veya buharlaşma.
Lf = +- 3.34 x 105J.kg-1 = donma veya erime.
Ld = +- 2.83 x 106J.kg-1 = depozisyon veya süblimleşme.
Soru: 2 kg su buharı yoğunlaştığında ne dar gizli ısı
serbest kalır?
Çözüm:
Verilen: mbuhar = 2 kg, Lv = 2.5x106 J . kg-1.
İstenen: ∆QE = ? J
∆QE = (2.5x106 J kg-1)(2 kg) = 5000 kJ
70
Termodinamiğin 1. Yasası
Kütlesi mhava olan bir hava parseline ∆QH kadar ısı
eklendiğinde ∆T kadar sıcaklığı değişmesinin yanısıra
parselin üzerinde veya parsel iş yapar. Bu bağıntıyı
gösteren denkleme Termodinamiğin 1. yasası denir.
∆QH
∆P
= C p ⋅ ∆T −
m hava
ρ
Eşitliğin sağ tarafındaki 1. terim hissedilen ısıyı ve
son terim ise birim kütle için basıncın değişmesine bağlı olarak
parselin büzüşmesi veya genleşmesi sonucu oluşan işi temsil etmektedir.
71
Termodinamiğin 1. yasasını anlamak
∆QH
∆P
= C p ⋅ ∆T −
ρ
m hava
Eşitliğin sağ tarafındaki son terimi yakından inceleyelim.
Basınç = F /A ve ρ = birim hacmin kütlesi olduğundan,
bu 2 terimin oranı = (kuvvet x yol) /kütle = birim kütlenin işi
72
Termodinamiğin 1. yasasını hidrostatik denklemle
birleştirirsek
 g
∆T = 
C
 p

∆
Q
H
 ⋅ ∆z +

m hava ⋅ C p

Eşitliğin sağ tarafındaki son terim (∆QΗ/mhava) eklenen ısının nedeni;
i) Radyatif ısınma
ii) Yoğunlaşırken gizli ısı,
iii)Azalan (dispatif)Türbülans enerjisi
iv) Kimyasal reaksiyonlardan olan ısı,
v) Hava veya parsel içindeki konvektif veya advektif etkileşim
Dikkat:
Konveksiyon ve adveksiyon enerji taşımaz, ancak hava parselini taşır.
73
Akılar
Genişleme
z
Konveksiyon
Adveksiyon
x
74
Soru: 10 kg kütleli bir hava parseli 10 dakika boyunca H = 100 W
ısı oranıyla ısıtıldığında, parselin sıcaklığı ne kadar değişir?
r = 0.001 gsubuharı/ghava
Çözüm:
Verilenler: H = 100 W; mhava = 10 kg; ∆z = 0; ∆t = 10 dak.
r = 0.001 gsubuharı/ghava
İstenen: ∆Τ = ? K
1. adım özgül ısıyı hesaplayalım;
Cp = (1004.67 J kg-1K-1)(1+0.84. 0.01) = 1013.11 J kg-1 K-1
2. Adım eklenen ısıyı bulalım;
∆QH=H.∆t = (100 W) (600 s) = 6x104 J.
3. Ve son adımda sıcaklık farkını bulalım;
 g
∆T = 
C
 p

 ⋅ ∆z + ∆QH

m hava ⋅ C p

∆T = (6x104J)/[(10kg).(1013.11 J kg-1K-1)] = 5.92 K
Kontrol: Birimler tamam. Fizik anlamlı.
75
Düşey Sıcaklık Gradyanı (Lapse Rate)
Γ = -∆T /∆z
1. Sürecin kendisinin düşey sıcaklık gradyanı
2. Sürecin çevresinin sıcaklık gradyanı
Adyabatik Düşey Sıcaklık Gradyanı
Adyabatik: Süreç ne dışarıdan ısı alır ne de verir.
∆QH = 0 => süreç adyabatiktir.
Eğer bir hava parseli adyabatik olarak yükseltilirse, içinde nem
olmadığını varsayarsak;
 g 
∆T
= −  = −0.98K / 100m = −9.8K / km
C 
∆z
 p
Kuru hava düşey sıcaklık gradyanı: Γd = 9.8K/km
76
Γd) nemli hava içinde
1. Kuru hava düşey sıcaklık gradyanı (Γ
uygulanabilir, ancak yükselen havanın doymamış olması
gerekir. Yani bulut ve yoğunlaşma olmaması durumunda
geçerlidir. Aksi durumda nemli hava düşey hava sıcaklık
gradyanı kullanılır.
2. Adyabatik düşey sıcaklık gradyanı, basınç terimleri
kullanılarak da elde edilir. Eğer İdeal gaz denklemini
Termodinamiğin 1. yasasına yerleştirirsek,
∆T  ∆P 
=

T
 P 
T2  P2 
=  
T1  P1 
Rd / Cp
veya
Rd / Cp
Rd/Cp=0.28571 (boyutsuz bir sabit) kuru hava için geçerlidir.
Ancak sıcaklık Kelvin dir.
77
Soru: Yerde 15oC olan doymamış bir hava parseli, 2km yüksekliğe
adyabatik olarak yükseltilirse sıcaklığı ne olur?
Çözüm:
Verilenler: T1=15oC ; ∆z = 2 km
İstenen: T2 = ?oC
∆ T T2 − T1
=
= − 98 o C / km
∆z
z 2 − z1
⇒ T2 = T1 + ∆ z ( − 9 .8) = 15 o C + ( 2 km )( − 9 .8 o C / km )
= − 4 .6 o C
Kontrol: Birimler tamam. Fizik anlamlı.
Tartışma: Suyun donması için yeterince soğumuştur.
78
Potansiyel Sıcaklık
• Tanım: Bir hava parseli üzerindeki kuru adyabatik
sıcaklık değişimlerini çıkardığımızda, elde edilen
sıcaklığa denir.
θ(z)=T(z) + Γd . z (Birimi oC veya K olabilir)
 P0 
θ = T ⋅ 
 P 
Rd / C p
P0 : referans seviye basıncı = 100 kPa alınır.
T : Kelvin olmak zorundadır
Potansiyel sıcaklık kuru adyabatik süreç için korunurdur.
79
Virtuel Potansiyel Sıcaklık
Eğer ortamda sadece subuharı varsa,
θv = θ.(1 + 0.61.r)
Ortamda hem subuharı hem de sıvı su varsa,
θv = θ.(1 + 0.61. (rs – rL))
r : karışma oranı
rs : doyma karışma oranı
rL: Sıvı su karışma oranı (bulutlar ve yağmur damlaları)
80
Soru: 500 m yükseklikte ve sıcaklığı T = 10oC olan havanın
potansiyel sıcaklığı nedir?
Çözüm:
Verilenler: z = 500m ; T = 10oC
İstenen: θ = ? oC
Ortamda sıvı su olmadığını farz edersek,
θ(z)=T(z) + Γd . z =>
θ (0.5 km) = 10oC + (9.8 oC/km) (0.5 km) = 14.9 oC
Kontrol: Birimler tamam. Fizik anlamlı.
Tartışma: Bu sıcaklık, 500 m yükseklikteki havanın, kuru
adyabatik olarak yeryüzüne indirilmesiyle elde edilen sıcaklığıdır.
Diğer bir deyişle, referans seviyesi yeryüzü seçilmiştir.
81
Termodinamik Diyagramlar
• Pratikte sıklıkla, çevre havanın düşey değişimi ile hava
parselinin karşılaştırmasına gerek vardır.
• Çünkü, hava parselin yükselmesi, bulutluluk ve fırtına
gelişimleri için bu gereklidir.
Her adımda termodinamik hesaplar yerine,
termodinamik ilişkileri gösteren basit bir diyagram
çizilir. Bunlar termodinamik diyagramlar olarak
adlandırılır.
Termodinamik diyagramlarda:
a) Yatay eksen sıcaklığı
b) Düşey eksen ise genelde basıncı gösterir.
82
Bir Termodinamik Diyagramda Bulunan
Değişkenler:
1.
2.
3.
4.
5.
Basınç
Sıcaklık
Kuru adyabatik sıcaklık oranı (lapse rate)
Doymuş (veya nem) adyabatik karışma oranı
Doymuş karışma oranı
83
Yükseklik (km)
Basınç (mb)
Skew-T log-P diagramı
84
Sıcaklık
(oC)
Kırmızı çizgiler : izotermleri
Düz yeşil çizgiler : Potansiyel sıcaklık
Kesikli yeşil çizgiler: Eş değer potansiyel sıcaklığı
(Bu 3 büyüklük 1000 mb seviyesinde başlar)
Mavi çizgiler: izobarları
Kesikli mor çizgiler : nem karışma oranı
(birimi diyagramın sağ alt köşesinde
g/kg verilmiştir)
85
Basınç (mb)
Skew diyagramı
86
Sıcaklık
(oC)
Excel kullanarak diyagramın hazırlanışı
A
B
C
D
E
Kuru Adyabatik Örnek
1
2
P(kPa)
T (oC)
T (oC)
T (oC)
T (oC)
3
100.00
60.00
40.00
20.00
0.00
4
90.00
50.12
30.71
11.31
-8.10
5
80.00
39.42
20.66
1.89
-16.87
6
70.00
27.72
9.66
-8.40
-26.46
7
60.00
14.76
-2.52
-19.81
-37.09
8
50.00
0.15
-16.26
-32.67
-49.07
9
40.00
-16.73
-32.13
-47.52
-62.91
10
30.00
-36.97
-51.15
-65.32
-79.50
11
20.00
-62.80
-75.43
-88.06
-100.69
P
T2 = T1 ⋅  0
 P1



Rd / C p
=((B$4+273.15)*($A5/$A$4)^0.28571)-273.15
87
EULER ISI BÜTÇESİ
Termodinamiğin 1. Yasası (Gözden Geçirme)
Eğer şekilde görülen sabit bir hacimden giren ısı akısı çıkan ısı
akısından az ise, ∆Q kadar ısı dışarıya atılıyordur. Dolayısıyla,
Termodinamğin 1. yasası gereği, ısı kaybı sıcaklığın düşmesine neden
olur.
∆x boyunca akının kendisi değil, ancak akı gradyanı (∆I veya ∆F)
sıcaklığın değişmesine neden olur. Akı gradyanına, akı diverjansı
denir.
1. ∆Fx / ∆x > 0 ise pozitif akı diverjansı (Çıkan akı girenden fazladır).
1. ∆Fx / ∆x < 0 ise akı konverjansı (Çıkan akı girenden azdır).
I veya F
Çıkan Akı
I veya F
Giren Akı
A
x
88
Eğer Giren ve Çıkan akıları tüm 3-boyut için yazarsak; Isı
Bütçesi, Isı Dengesi veya Isı Korunum Denklemi elde edilir.
• Sabit hacim = A. ∆x için, ısı dengesi denklemi;
∆T
1
= −
∆t
ρ ⋅C
p
∆I y
 ∆Ix
∆S0
∆I z 
+
+

+
∆y
∆z  C p ⋅ ∆t
 ∆x
∆So : birim kütle için (Jkg-1) iç ısı enerjisi. Örn, Gizli ısı v.b.
• Kinematik-Akı (F) için ısı dengesi denklemi;
∆Fy
 ∆ Fx
∆T
∆ Fz 
∆S0
= −
+
+
+
∆t
∆y
∆z  C p ⋅ ∆t
 ∆x
∆Fy
 ∆ Fx
∆θ
∆ Fz 
∆S0
= −
+
+
+
∆t
∆y
∆z  C p ⋅ ∆t
 ∆x
89
Soru: Deniz seviyesinde, her bir kenarı 20 m olan bir küp hava
olduğunu varsayınız. Bu küpün solundan doğu yönlü 3 Wm-2 bir
ısı akısının ve sağından ise batılı 4Wm-2 bir ısı akısının girdiğini
varsayınız. İç ısı kaynağı ve başka diğer akılar mevcut değildir.
Her bir kenardaki kinematik ısı akısını ve hangi oranda sıcaklığın
değiştiğini hesaplayınız?
Çözüm:
Verilenler: Ixsağ = -4Wm-2 ; Ixsol=3Wm-2; ∆x = 20 m
İstenen: Fxsağ = ? K.m/s ; Fx sol = ? K.m/s; ∆T/∆t = ?K/s
Fx sol = (3 Wm-2)/(1231) = 2.437x10-3K.m/s
Fx sağ = (-4 Wm-2)/(1231)= -3.249x10-3K.m/s
Ix sol veya (+)
Fx sol
A
x
Ix sağ veya (-)
Fx sağ
90
Akı gradyanı:
[
(−3.249 × 10 −3 ) − (2.437 ×10 −3 )
∆Fx Fsağ − Fsol
=
=
[20 − 0]
xsağ − xsol
∆x
]
= -2.843 ×10-4 K / s
∆Fx
⇒ ∆T ∆t = −
= +2.843 ×10 − 4 K / s
∆x
Kontrol: Birimler tamam. Serbest cisim diyagramı uygun.
Tartışma: Isınma oranı yaklaşık 1 K /saat dır.
91
Akı Gradyanlarının Bileşenleri
∆Fx ∆Fx
=
∆x
∆x
∆Fy
∆y
=
∆Fx
+
∆x
adv
∆Fx
+
∆x
kond
∆Fx
+
∆x
türb
∆Fy
∆Fy
∆Fy
∆Fy
∆y
∆Fz ∆Fz
=
∆z
∆z
+
adv
∆y
∆Fz
+
∆z
adv
+
kond
∆y
∆Fz
+
∆z
kond
+
türb
∆y
∆Fz
+
∆z
türb
rad
rad
rad
92
1. Adveksiyon:
• Adeveksiyon: rüzgar ile taşınan anlamına gelir.
• Sıcaklık adveksiyonu: Bir bölgeye veya bir bölgeden
rüzgarla taşınan ısı anlamına gelir.
Fx adv = U . T
Fy adv = V . T
Fz adv = W . T
• Düşey harekete ortalama rüzgarla ise adveksiyon
denir; yok eğer kaldırma kuvvetindense konveksiyon
olarak adlandırılır.
93
Adveksiyon (devamı)
• Isı bütçesi denklemi ham akıları değil, akı
gradyanlarını kullanmaktadır. Dolayısıyla;
∆ F x adv
∆x
∆ F y adv
∆y
∆ F z adv
∆z
=
U ( T sa ğ − T sol )
x sa ğ − x sol
∆T
= U ⋅
∆x
∆T
= V ⋅
∆y
∆T

= W ⋅
+ Γd 
 ∆z

94
Soru: Farz edelim ki ortalama hava sıcaklığı yükseklikle
soğumaktadır; öyle ki z = 200 m de T = 15oC ve z = 1000 m de
T = 10oC olacak şekilde lineer değiştiğini düşünelim. Eğer
ortalama düşey rüzgar hızı soğuk havayı yukarıdan aşağıya doğru
itiyorsa, o zaman z = 600 m de Adveksiyon ile soğuma oranı ne
olur? W = - 0.1 m/s ve diğer ısıma süreçlerini yok kabul ediniz.
Çözüm:
Verilenler: W= -0.1 m/s; z = 600 m;
∆T/∆z = (10-15)/(1000-200) = - 0.00625 oC/m
İstenen: ∆T/∆t = ?oC/s
∆T/∆t = - ∆Fz adv/∆z = -W(∆T/∆z + Γd)
= - (-0.1 m/s).(-0.00625 + 0.0098 oC/m)
= + 3.55x 10-4 oC/s = 1.28 oC /saat
Kontrol: Birimler tamam. Fizik anlamlı.
Tartışma: Pozitif işaret soğumayı değil ısınmayı gösterir.
95
2. Kondüksiyon ve Yüzey Akıları
Tanım: Moleküller birbiriyle temas halindeyken, ısı
taşımasına denir. Kondüksiyon süreci maddenin 3 hali
içinde geçerlidir. Yani katılar, sıvılar ve gazlar için
ortamda rüzgar olsun veya olmasın geçerlidir. Bu tür ısı,
genelde yerden atmosfere veya yeryüzünden yerin
içlerine doğru görülür.
Düşeyli taşınan dokunmatik (kondüksiyon) ısı miktarı:
∆T
I z kond . = − k ⋅
∆z
Deniz seviyesinde standart
k: moleküler ısı iletkenlik katsayısı koşullarda,
k= 2.53x10-2 W.m-1.K-1
96
Atmosferde, gerek x (batı-doğu) ve gerekse y (güney-kuzey)
yönlerinde, ısı iletkenliği ihmal edilecek kadar küçüktür.
∆ Fx kond. ∆ F y kond.
≈
≈0
∆x
∆x
97
Soru: 300 W m-2 ısı akısının, yerden 1 mm yukarıdaki atmosfere
iletilmesi için ne kadar sıcaklık farkı gereklidir?
Çözüm:
Verilenler: Iz kond. = 300 W m-2 , ∆z = 1 mm = 0.001 m;
k= 2.53x10-2 W.m-1.K-1
İstenen: ∆T = ? oC
∆T
I z kond . = − k ⋅
⇒ ∆T = − I z ∆z / k
∆z
∆ T = − (300Wm − 2 )( 0.001m ) / 2.53 × 10 − 2 Wm −1 K −1
∆ T = −11 .9 o C
Kontrol: Birimler tamam. Fizik anlamlı.
Tartışma: Havanın temasta olduğu yerden, aşağı yukarı 12oC daha
soğuk olmalı ki bu kadar ısı iletilebilsin. Gerçek atmosferde bu sıcaklık
98
farkı genel gözlemlenebilir bir durumdur.
Efektif Isı Akısı
Genelde, atmosferde çalkantı (türbülans) ve kondüksiyon birlikte
hareket eder. Çoğunlukla kondüksiyonla ısı taşınımı önemliyse
türbülans önemsiz, tersi türbülans önemliyse kondüksiyon
önemsizdir. Ancak, ikisi de önemliyse, yani birleştirilirse;
Efektif yüzey türbülans ısı akısı elde edilir.
FH = CH . M . (θyer - θhava) veya
FH = CH . M . (Τyer - Τhava)
M : 10 m’deki ortalama rüzgar hızı büyüklüğü,
Thava : 10 m’deki hava sıcaklığı,
Tyer : yeryüzü sıcaklığıdır.
CH : boyutsuz, yığınsal (bulk) ısı iletim katsayısı
Düzgün yüzeyler üzerinde: 2x10-3
Orman ve düzgün-olmayan yüzeyler üzerinde: 2x10-2
99
Yerden 1-2 km yukarıdaki atmosfer (troposfer) tabakasına,
atmosferik sınır tabaka denir (ABL).
Kuvvetli güneş ışınımın ve konveksiyonun olduğu sakin havalı bir
günde, yükselen hava parselleri (termalleri) bu tabakada
meydana gelir. Bu tür ABL tabakaya karışım tabakası (ML)
denir. Bu durumda, yüzey akılar:
FH = bH . wB . (θyer – θML) veya
FH = aH . w* . (θyer – θML)
θML: 500 m’deki (ML’nin ortasında) potansiyel sıcaklığı,
aH : 0.0063 : karışım-tabaka taşınım katsayısıdır.
wb : yükselen parsel (konvektif) hız ölçeği
w*: Deardorff hızı (bir başka konvektif hız ölçeği)
100
Türbülans Isı Akısı
F z üst − F z alt
∆ F z türb .
=
∆z
zi
∆ F z türb . − 1 . 2 F H
≈
∆z
zi
zi : ABL derinliğidir (200 m ile 2 km arasında değişir)
101
Radyatif Isı Akısı
∆ F x rad . ∆ F y
≈
≈0
∆x
∆y
∆ F z rad .
≈ − 0 . 1 ile − 0 . 2 K / saat
∆z
∆T
∆z
x, y,z

= − U


NET ISI BÜTÇESİ

∆T
∆T 
∆ Fz Lv m yoğuş.
⋅
+V ⋅
− − 0 .1K / sa .−
+
Rad .
∆x
∆y 
∆ z C p m hava ∆ t
Türb
.
Advek .

Gizli Isı
102
GÖRÜNEN SICAKLIK TÜRLERİ
1. Rüzgar Soğuğu:
Trüz
 M + M0 

= Tderi − 
 M0 
0.21
(Tderi − Thava )
Tderi: Vücut derisi sıcaklığı = 33oC
Mo: Ortalama bir insanın yürüme hızı = 2 m /s
2. Hissedilen Sıcaklık veya Isı İndeksi
HI = -42.379 + 2.04901523T + 10.14333127.RH - 0.22475541.T.RH
-0.00683783T2 - 0.05481717.RH2 + 0.00122874.T2.RH + 0.00085282.T.RH2
-0.00000199.(T.RH)2
RH: Bağıl nem
T > -57 °F ve T < 57 °F için geçerlidir
103