04.05.2014 Barış DEMİR
Ayrıca, şekilde P noktası çemberin dışında olduğundan, | MP |> r
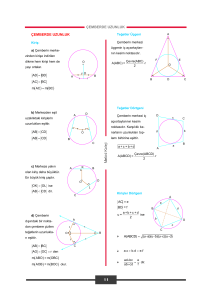
ÇEMBERDE KUVVET FONKSİYONU
olacaktır. Bu nedenle P noktasının kuvveti
Düzlemde merkezi M (a, b) ve yarıçapı r olarak verilen bir çembere
K (P ) =| MP |2 -r 2 > 0
göre, bir P ( x0 , y0 ) noktasının kuvveti
dır.
K : R2 R , K (P ) =| MK |2 -r 2
fonksiyonu ile tanımlanır. Bu fonksiyon özünde, R2 de verilen bir P
noktasını, R de bir sayı ile eşlemektedir. Fonksiyonun kuralında
görüldüğü üzere bu sayı, merkez ile P noktası arasındaki uzaklığın
karesinden, yarıçapın karesinin çıkarılmasıyla elde edilmektedir.
Fonksiyonda koordinatlar yerine yazılırsa,
2
O halde, çemberin dışındaki bir noktanın bu çembere göre kuvveti
daima pozitiftir.
2. Soldaki şekildeki gibi, çemberin dışındaki bir P noktasından, [PT]
teğetini ve çemberi A ve B noktalarında kesen PB kesenini çizelim.
B
2
K (P ) = ( x 0 - a ) + ( y 0 - b ) - r 2
T
olduğu göz önünde tutulursa, çember denklemi ile fonksiyonun ne
derece ilgili olduğu anlaşılmaktadır.
P
A
B
2
2
olduğu görülür. Çemberin denkleminin ( x - a ) + ( y - b ) = r 2
T
Sağdaki şekilde görüleceği üzere, [BT] ve [AT] çizilirse
) = m(PBT
) olacağından PBT üçgeni ile PTA üçgeni
m( ATP
Örnek 1
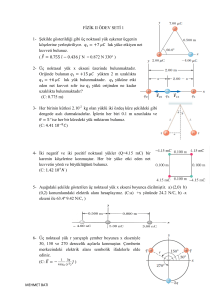
(x - 1)2 + ( y + 3)2 = 13 çemberine göre aşağıdaki noktaların
benzer olacaktır. Bu benzerlik gereği
kuvvetlerini hesaplayınız.
| PT |
| PB |
=
| AP |
| PT |
olduğundan,
a. (5,7) b. (3,0) c. (2, -1)
| PT |2 =| PA | ⋅ | PB |
Çözüm:
Doğrudan doğruya fonksiyonun kuralını ilgilendiren bir örnek
olduğundan
2
P
A
bulunur.
Birinci yorumda teğetin karesinin aslında P noktasının kuvvetine
eşit olduğunu göstermiştik.
2
a. K (P ) = ( 5 - 1 ) + ( 7 + 3 ) - 13 = 103
O halde,
K (P ) =| PA | ⋅ | PB |
b. K (P ) = (3 - 1)2 + (0 + 3)2 - 13 = 0
dir.
c.
2
K (P ) = ( 2 - 1 )
+ (-1 + 3) - 13 = -8
2
Demek ki, P noktasının kuvveti, aynı zamanda bu noktadan çizilen
herhangi bir kesenle de ifade edilebilir. Bu durumu aşağıdaki gibi
genelleyebiliriz.
P
A
bulunur.
Bu örnekte görüldüğü üzere, bir noktasının verilen bir çembere göre
kuvveti pozitif, negatif veya sıfır olabilir. Şimdi bunların ne anlama
geldiğini anlamaya çalışalım.
B
C
Kuvvet fonksiyonunun geometrik yorumu
1. Şekildeki gibi, çemberin dışında bir P noktası verilsin.
D
P
| PA | ⋅ | PB |=| PC |⋅ | PD |
M
T
Tanım gereği, K (P ) =| MP | -r dir. Öte yandan, çizilen [PT]
2
3.
P
2
teğetine göre, PMT dik üçgeninde | PT |2 =| MP |2 -r 2 dir.
M
P noktası çemberin üzerinde olduğunda ise
| MP |= r olacağından K (P ) = 0 dır.
Esasında bu kuvvetin tanımından da
sezilebilirdi.
O halde, çemberin dışındaki bir P noktanın kuvveti, bu noktadan
çembere çizilen teğet parçasının karesine eşittir.
K (P ) =| PT |2
O halde, çembere ait bir P noktasının bu çembere göre kuvveti 0 dır.
04.05.2014 Barış DEMİR
Demek ki, P noktasının kuvvetini, bu noktadan geçen herhangi bir
kiriş ile aşağıdaki gibi genelleyebiliriz.
4. Şekildeki gibi çemberin içinde bir P noktası verilsin.
B
D
P
M
B
A
Öncelikle | MP |< r olduğundan, K (P ) =| MP |2 -r 2 < 0
O halde, çemberin içindeki bir P noktasının bu çembere kuvveti
negatiftir.
Ayrıca, şekildeki gibi P noktasından geçen en kısa kiriş [AB] yi
çizersek, [MP ] ^ [BA] olduğundan,
| PA |2 = r 2 - | MP |2
olur. Dikkat edilirse bu eşitliğin sağ tarafı P noktasının kuvvetinin
negatifine eşittir.
O halde, çember içindeki bir P noktasının bu çembere göre
kuvvetinin mutlak değeri, P noktasından geçen en kısa kirişin
yarısının karesine eşittir.
| PA |2 = -K (P )
5. Soldaki şekildeki gibi, çemberin içindeki bir P noktasından geçen
en kısa [AB] kirişi ile rastgele bir [CD] kirişi çizelim.
B
B
D
P
D
P
A
C
A
C
Sağdaki şekilde olduğu gibi, [BD] ve [CA] çizilirse
) = m(DCA
) ve m(BPD
) = m( APC
) olduğundan, DBP
m(DBA
üçgeni ile ACP üçgeni benzerdir. | PA |=| PB | ve bu benzerlik
| PD |
| PB |
olduğundan
=
| PA |
| PC |
| PA | ⋅ | PB |=| PC | ⋅ | PD |
yani
| PA |2 =| PC | ⋅ | PD |
olur.
Dikkat edilirse eşitliğin solu, kuvvetin negatif işaretlisine eşittir
(bir önceki çıkarım).
O halde,
-K (P ) =| PC | ⋅ | PD |
dir.
C
| PA | ⋅ | PB |=| PC | ⋅ | PD |
olduğunu görebiliriz.
gereği
A
P