3. BÖLÜM
ELEKTRİK DEVRELERİ
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
2A
3Ω
1A
6Ω
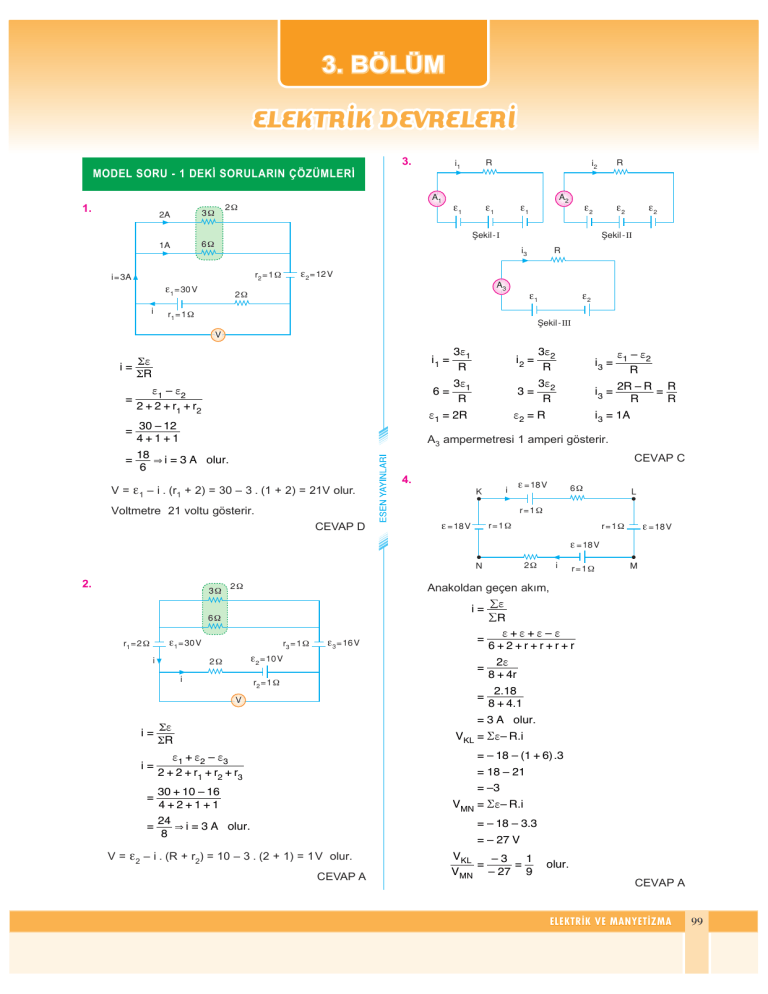
3.
A1
2Ω
i1
R
ε1
ε1
A2
ε1
ε2
ε2
fiekil- I
i
R
ε2 = 12 V
r2 = 1 Ω
ε1 = 30 V
ε2
fiekil- II
i3
i = 3A
R
i2
A3
2Ω
ε1
r1 = 1 Ω
ε2
fiekil- III
V
i=
Σf
ΣR
f1 – f2
=
2 + 2 + r1 + r2
V=
3f1
R
i2 =
3f2
R
i3 =
f1 – f2
R
6=
3f1
R
3=
3f2
R
i3 =
2R – R R
=
R
R
f1 = 2R
30 – 12
=
4+1+1
=
i1 =
i 3 = 1A
f2 = R
A3 ampermetresi 1 amperi gösterir.
18
& i = 3 A olur.
6
CEVAP C
ε1 – i . (r1 + 2) = 30 – 3 . (1 + 2) = 21V olur.
4.
i
K
Voltmetre 21 voltu gösterir.
ε =18V
6Ω
L
r=1Ω
CEVAP D
ε =18V
r=1Ω
ε =18 V
r=1Ω
ε =18V
2Ω
N
2.
3Ω
2Ω
6Ω
ε1 = 30 V
r1 = 2 Ω
i
r3 = 1 Ω
ε3 =16V
ε2 = 10 V
2Ω
i
i=
Σf
ΣR
i=
f 1 + f 2 – f3
2 + 2 + r1 + r2 + r3
=
M
=
2f
8 + 4r
=
2.18
8 + 4.1
= 3 A olur.
VKL = Rf– R.i
= – 18 – (1 + 6) .3
= 18 – 21
= –3
30 + 10 – 16
4+2+1+1
VMN = Rf– R.i
24
=
& i = 3 A olur.
8
V=
r=1Ω
Anakoldan geçen akım,
/
i= f
/R
f+f+f–f
=
6+2+r+r+r+r
r2 = 1 Ω
V
i
= – 18 – 3.3
= – 27 V
ε2 – i . (R + r2) = 10 – 3 . (2 + 1) = 1 V olur.
CEVAP A
VKL
–3
1
=
=
VMN – 27 9
olur.
CEVAP A
ELEKTRİK VE MANYETİZMA
99
5.
ε2 = ε
R2 = 3r
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
r2 = r
i
1.
V
R
R
R
ε1 = 2ε
R1 = 2r
i
R
A1
r1 = 2r
A2
ε
Devreden geçen akım,
ε
ε
ε
/f
i=
/R
=
ε
ε
fiekil- I
f1 – f2
R 1 + R 2 + r1 + r2
fiekil- II
Şekil-I
deki devrede:
_________________
2f – f
2r + 3r + 2r + r
f
olur.
=
8r
=
i1 =
3f
2R
i2 =
Voltmetrenin gösterdiği değer,
3f
i 1 2R 3
=
=
4
i2
2f
R
V = f2 + i. (R 2 + r2)
= f+
Şekil
- II deki devrede:
__________________
f
. (3r + r)
8r
f
2f
=
R
R
2
olur.
CEVAP C
f
= f + .4r
8r
= f+
=
f
2
3
f olur.
2
2.
R2 =2r
CEVAP E
R3 =2r
A
6.
K
R
L
ε
R
R
2r
R
ε1
ε2
r1 = 0
r2 ≠ 0
V1
V2
fiekil- I
fiekil- II
K
K
ve L anahtarları açık iken:
______________________
f
i1 =
R 1 + R 3 + 2r
V1 =
ε1
K anahtarı kapalı ekin, V1 = ε1 olur.
Değişmez.
K ve L anahtarları kapalı iken:
________________________
f
i2 =
3r + r
f
olur.
=
4r
f
i 1 6r 4 2
olur.
=
= =
i2
6 3
f
4r
Şekil-II
deki devrede:
__________________
f
f
& V2 = f –
i2 =
.r
R+r
( R + r)
›
›
f
f
& V2 = f –
.r
R
R
+r
+r
2
2
Azalır.
CEVAP D
100
ELEKTRİK VE MANYETİZMA
f
2r + 2r + 2r
f
=
olur.
6r
=
ı
i2 =
ε
2r
Şekil-I
deki devrede:
_________________
K anahtarı açık iken,
L
R1 =2r
CEVAP C
3.
5.
4Ω
R =4r
K
V
3Ω
R =4r
12 Ω
r = 1Ω
i
ε› = 45 V
r› = 1 Ω
ε = 15 V
ε = 15 V
ε = 15 V
r = 1Ω
r = 1Ω
r = 1Ω
ε = 15 V
ε = 15 V
ε = 15 V
r = 1Ω
r = 1Ω
r = 1Ω
ε = 15 V
ε = 15 V
ε = 15 V
r = 1Ω
r = 1Ω
r = 1Ω
A
ε =15V
L
ε
ε
r
r
ε
ε
r
r
K ve L anahtarları açık iken:
_______________________
2f
2f
f
i1 =
=
=
4r + 2r 6r 3r
Anakoldan geçen akım,
i=
=
K ve L anahtarları kapalı iken:
________________________
Σf
ΣR
i2 =
45 – 15
3+1+1
f
i1
1
olur.
= 3r =
i 2 2f 2
3r
30
=
5
=6A
2f
2f
=
2r + r 3r
olur.
CEVAP B
ı
V = i . R = 6 . 3 = 18 V
Voltmetre 18 voltu gösterir.
CEVAP E
6.
3Ω
2Ω
ε =25V
K
L
r=1Ω
6Ω
3Ω
4.
R2 = 12 r
L
r=1Ω
i
ε
2r
R1 = 4 r
ε
ε =25V
ε =25V
r=1Ω
r=1Ω
i
ε =25V
2r
ε
ε› =25V
r› = 1
–Ω
3
r=1Ω
V
2r
K
ε =25V
r=1Ω
ε =25V
ε
i=
2r
=
K ve L anahtarları açık iken:
_______________________
f+f–f
f
i1 =
=
4r + 2r + 2r + 2r 10r
=
K ve L anahtarları kapalı iken:
________________________
f+f–f
f
=
i2 =
3r + 2r + 2r + r 8r
f
i 1 10r
8
4
=
=
=
olur.
f
i2
10 5
8r
Σf
ΣR
›
ε +ε+ε–ε
3+2+1+1+1+
1
3
50
25
3
= 6 A olur.
VKL = Σε – ΣRi
=
ε – 3i
= 25 – 3 . 6
= 7 V olur.
CEVAP E
CEVAP B
ELEKTRİK VE MANYETİZMA
101
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
ε4
K
5Ω
L
Ohm yasasına göre, Şekil-I deki
ε› = 12 V
ε2 = 12 V
i1 =
r› = 1Ω
ε3 = 12 V
r1 = 2Ω
Anakoldan geçen akım i = 2 A olduğundan,
Σf
ΣR
f1 + f –f4
f
.t
R 1
t1 =
q.R
= 6 saat olur.
f
›
R + r1 + r + r4
3f
i2 =
= 3.i
R
32 – f4
2=
9
R
i2
ε
ε
ε
+ – + – + –
fiekil-ΙΙ
18 = 32 – f4
Üreteçler özdeş ve seri bağlandığından her bir
üreteçte toplanan yükler q dur.
f4 = 14 V olur.
Bu durumda devreden t2 süre akım geçerse,
q = i2 . t2
ε4 emk lı üretecin verimi,
Verim =
ε 4 – i.r4 14 – 2.1 6
=
=
olur.
ε4
14
7
CEVAP D
2.
4Ω
ε4 =10V
r4 = 1Ω
A
ε1 =30 V
r1 =1 Ω
q=
3f
.t
R 2
t2 =
q.R 1
= .6 = 2 saat
3f
3
3Ω
12 Ω
ε2 = 10 V
ε3 = 20 V
r3 = 2Ω
i
Şekil-III teki üreteçler birbirlerine
paralel olduklarından devrenin
toplam emk sı herhangi bir üretecin emk sına eşittir.
r2 = 1Ω
i3 =
ε› = 20 V
Σf
ΣR
›
=
f – f4
3+1+1
=
20 – 10
5
i3 =
i3
i
f
olur.
=
=
3 3R 3
›
i3 + ε –
›
i3
ε
+ –
›
i3 + ε –
i3
R
fiekil-ΙΙΙ
Her bir pilin üzerinde toplanan yük q olduğundan
pillerin akım verme süresi t3 ise,
ı
q = i3 . t3
= 2A
Ampermetre 2 amperi gösterir.
ε4 emk lı üretecin verimi,
Verim =
f
=i
R
Her bir üretecin üzerinden geçen
akım,
r› = 1Ω
›
f4 – i.r4 10 – 2.1
=
= 0, 8
f4
10
% Verim = 0,8.100 = % 80 olur.
102
q=
geçen akım,
20 + 12–f4
2=
5+2+1+1
i=
fiekil-Ι
Şekil-II deki devreden
›
i
i1 + ε –
q = i1 . t1
r3 = 2Ω
i=
f
= i olsun.
R
Üreteçte depolanan yük q ise,
ε1 = 20 V
r2 = 2Ω
i=
R
devreden geçen akım,
r4 = 1Ω
i=2A
1.
ELEKTRİK VE MANYETİZMA
q=
f
.t
3R 3
t3 =
3q.R
= 3.6 = 18 saat olur.
f
CEVAP D
CEVAP E
2.
Şekil-I deki devrenin eşdeğer direnci,
Reş = 2r + 2r + 2r = 6r olur.
Anakoldan geçen akım,
3r
ε
+ –
i2
r 2r
=
= r olur.
n 2
=
2f
8
2r
ε
+ –
+ –
i2
ε
ε
+ –
+ –
r=2Ω
r=2Ω
fiekil-ΙΙ
Her bir pilin üzerindeki yük q, pillerin ömrü t2 ise,
›
i2
q = i2 . t2
2r
ε
R=4Ω
f
=
olur.
4
›
i2
f
.t
4 2
q=
2r
Şekil-Ι de bulduğumuz q = 2ε
kullanırsak,
Anakoldan geçen i2 akımı,
2f =
1 f 1
3
f
= . = .3i = i olur.
5r 5 r 5
5
değeri burada
f
.t
4 2
t 2 = 8 saat olur.
Üreteçlerin her birinin yükü q ise, Şekil-I deki devre için,
Şekil-III teki devrede toplam
direnç,
q = i1 . t1
r
2
= 4 + = 5X
2
2
f
i3 akımı, i 3 =
olur.
5
f
.t
3r 1
R=4Ω
i3
ε
›
R efl = R +
3q.r
t1 =
= t olarak verilir.
f
i3
+ –
›
i3
ε
r=2Ω
+ –
Her bir pilden geçen akım,
Şekil-II deki devrede üreteçlerin üzerlerinden
geçen akım,
i
›
1 f
f
i2 = 2 = . =
olur.
2 2 5r 10r
r=2Ω
i3 1 f
f
olur.
= . =
2 2 5 10
›
i3 =
fiekil-ΙΙΙ
Pillerin üzerindeki yük q, pillerin ömürleri t3,
ı
q = i3 . t3
›
q = i 2 .t 2
q = 2ε değerini burada yazarsak,
10q.r
f
.t & t 2 =
10r 2
f
f
.t
10 3
t3 = 20 saat olur.
2f =
q.r t
= eşitliği burada yerine yazarsak,
f
3
t 2 = 10.
2f
4+2+2
+ –
Reş = reş + 4r = r + 4r = 5r,
q=
=
4r
Üreteçler 4r direncine seri bağlı
olduğundan, devrenin eşdeğer
direnci,
q=
2f
R+r+r
ε
2r
Şekil-II deki üreteçlerin eşdeğer
direnci,
i2 =
i2 =
i3
2f
f
i1 =
=
= i olur.
6r 3r
refl =
Şekil-II deki devreden geçen akım,
6r Refl=2r
t 10
=
t
3
3
CEVAP C
olur.
CEVAP C
3.
Ohm yasasına göre, Şekil-I deki
R=4Ω
devreden geçen akım,
i1 =
f
f
f
olur.
=
=
R+r 4+2 6
i1
Pilin üzerinde depolanan yük q
ise, bu yükün direnç üzerinden
geçme süresi yani pilin ömrü t1,
q = i1 . t1
q=
f
.t
6 1
t1 =
6q
q
= 12 &
= 2 saat olur.
f
f
ε
+ –
r=2Ω
fiekil-Ι
4.
Şekil-I deki devreden geçen akım,
f
f
f
i1 =
=
=
R + r 8 + 2 10
pilin yükü q ise, akım verme
süresi t1,
q = i1 . t1
q=
8Ω
K
i1
f
.t
10 1
10q
t1 =
f
10q q
20 =
& = 2 olur.
f
f
+
ε
–
r=2Ω
fiekil-Ι
ELEKTRİK VE MANYETİZMA
103
Şekil-II deki devredeki
paralel bağlı üreteçlerin
direnci,
›
r =
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
i2/2 + ε–
r 2
= = 1X
2 2
ε
r=2Ω
+ –
i2/2 + ε–
r=2Ω
r=2Ω
L
1.
Ι4=6A
Ι2=4A
devredeki toplam direnç,
Reş = rı + r + 8
=1+2+8
= 11 Ω olur.
i2
14A
Ι
8Ω
fiekil-ΙΙ
14A
2A
Ι1
4A
Anakoldan geçen i2 akımı,
i2 =
I +I4 + 2 + 4 = 14
f + f 2f
olur.
=
11
11
I + 6 + 2 + 4 = 14 ⇒ I = 2A olur.
Bu devrede iki pil birbirine paralel, diğeri bunlara
seri bağlıdır. Paralel bağlı pillerden geçen akım az
olacağından önce seri pil, daha sonra paralel piller
biter. Seri pil bitene kadar geçen süre ts olsun.
CEVAP E
2.
3R
Seri pil üzerindeki yük q,
R1
q = is . ts
Ι=10A
2f
q=
.t
11 s
ts =
R
I1 akımı, I1 + 7 = 10 ⇒ I1 = 3A olur.
3Ι›
Ι=10A
ε
›
2R
R
Ι2
2Ι›
3Ω
2Iı + 3Iı = I
ε
i2
R
R1
R2
2Ω
r=2Ω
5Iı = 10 ⇒ Iı = 2A olur.
r=2Ω
8Ω
›
i2
q
= .t
2 2 p
I2 akımı, I2 = 3Iı = 3.2 = 6A olur.
I
3 1
Akımların oranı, 1 = =
olur.
I2 6 2
3.
3X
11q
f
.t & t p =
f
11 p
q
= 2 değerini burada yazarsak,
f
11q
tp =
= 11.2 = 22 saat olur.
f
Bu durumda Şekil-II deki devrenin akım verme süresi,
t2 = ts + tp = 11 + 22 = 33 saat olur.
CEVAP E
4A K 3A
•
1A
f1=20V
CEVAP A
4X
1
•
I. ‹LMEK
II. ‹LMEK
f2=30V
2
2X
›
q = i 2 .t p
ELEKTRİK VE MANYETİZMA
3R
R2
3R
11 saat içinde paralel bağlı piller üzerinden geçen
i2
olduğundan q yüklerinin yarısı boşalır. 11 saat
2
q
olur. Yeni
durumsonra pillerin üzerindeki yük
›
2
i2
olur.
da her bir pilin üzerinden geçen akım
2
Paralel bağlı pillerin boşalma süreleri tp ise,
104
Ι2
olur.
11 saat sonra seri pil biter. Paralel piller devreye
akım vermeye devam eder. Yeni durumda devremiz şekildeki gibi olur.
q=
3R
7A
Ι1
11 q 11
. =
.2 = 11 saat
2 f
2
Seri bağlı üreteç devreden çıktığından devredeki toplam gerilim azalır.
Bu durumda anakoldan
geçen akım,
›
f
f
i2 =
olur.
=
R efl 11
R
•L
6X
I. İLMEK:
f
20
= 4A olur.
i1 = 1 =
RR
5
II. İLMEK:
f
30
i2 = 2 =
= 3A olur.
RR
10
Şekilde görüldüğü gibi, KL kolundan geçen akım 2
yönünde 1 amper olur.
CEVAP B
4.
3Ω
Ι1
ε1=25V
Ι.ilmek
+
–
' ve ( nolu denklemler ortak çözülecek olursa,
ε2=20V
Ι2
+ –
2Ω
(–7).2Ι1 – Ι2 = 1.(–7)
3Ι1 – 7Ι2 = –15
+______________________
ΙΙ.ilmek
2Ω
5Ω
–14Ι1 + 7Ι2 = –7
Ι2
Ι1
3Ι1 – 7Ι2 = – 15
+______________________
Ι. ilmek için K.G.Y yazılacak olursa,
11Ι1 = 22
Σε – ΣR.Ι = 0
Ι1 = 2A olur.
25 – (3.Ι1 + 2.Ι1+ 2.(Ι1 + Ι2)) = 0
7Ι1 + 2Ι2 = 25 ... '
Ι1 akımı ' nolu denklemde yerine yazılırsa,
2.2 – Ι2 = 1
ΙΙ. ilmek için K.G.Y yazılacak olursa,
4 – Ι2 = 1 ⇒ Ι2 = 3A olur.
Σε – ΣR.Ι = 0
20 – (5.Ι2 + 2.(Ι1 + Ι2)) = 0
3Ω luk direncin üzerinden geçen akım,
2Ι1 + 7Ι2 = 20 ... (
Ι = Ι2 – Ι1 = 3 – 2 = 1A olur.
CEVAP B
' ve ( denklemleri ortak çözülecek olursa,
(2).7Ι1 + 2Ι2 = 25.(2)
(–7).2Ι1 + 7Ι2 = 20.(–7)
+______________________
14Ι1 + 4Ι2 = 50
– 14Ι1 – 49Ι2 = – 140
+________________________
6.
ε1=20V
+ –
− 45Ι2 = –90
Ι2 = 2A olur.
2Ω
5Ω luk direncin üzerinden geçen akım 2A olur.
ε2=10V
Ι
+ –
Ι
Ι.ilmek
2Ω
–
ε3=5V +
1Ω
V
Ι
3Ω
Ι
CEVAP D
Ι. ilmek için K.G.Y uygulanırsa,
Σε – ΣΙ.R = 0
5.
Ι1
ε1=3V
ε2=4V
Ι2
+ –
(10 + 5) – (3.Ι + 2.Ι) = 0
– +
Ι2
1Ω
Ι1
Ι.ilmek
3Ω
ΙΙ.ilmek
2Ω
+
ε =19V
– 3
4Ω
Ι1
Ι2
Ι = 3A olur.
Voltmetrede okunan değer,
V = Ι.R = 3.2 = 6 volt olur.
CEVAP C
Ι. ilmek için Kirchhoff’un gerilim yasası yazılırsa,
Σε – Σ Ι.R = 0
3 – (1.Ι1 + 2.Ι1 +(Ι1 – Ι2).3) = 0
2Ι1 – Ι2 = 1 ... '
ΙΙ. ilmek için Kirchhoff’un gerilim yasası yazılırsa,
Σε – Σ Ι.R = 0
(19 – 4) – (4.Ι2 + 3.(Ι2 – Ι1)) = 0
3Ι1 – 7Ι2 = – 15 ... (
ELEKTRİK VE MANYETİZMA
105
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
1.
i=4A
Pü = I.Vü
5Ω
400 = I.100
ε› = 24 V
r› = r
ε = 12 V
r
6A
VR = I.R
140 = 4.R
R direncinin gücü,
P = I2.R
= 42.35
6A
= 560 W olur.
A
12 Ω
I. ve II. yargılar doğru, III. yargı yanlıştır.
3Ω
3Ω
ε = 20 V
r = 1Ω
r = 1Ω
ε = 20 V
ε = 20 V
r = 1Ω
r = 1Ω
5.
ε› = 20 V
r› = 1Ω
f +f
6+2+1+1
=
60
10
Ιf
Ιü
f›r›n
ütü
Ι=10A
220V
Pü = Iü.Vü
660 = Iü.220
=6A
Iü = 3A olur
I. yargı doğrudur.
P = i22 . R = 22 . 6 = 4 . 6 = 24 W olur.
CEVAP D
Fırının üzerinden geçen akım,
I = Iü + If
Cihazın üzerinden geçen akım,
10 = 3 + If
P = I.V
If = 7.A olur.
500 = I.100 ⇒ I = 5A olur.
II. yargı doğrudur.
Pilin gerilimi 200 V, cihazın üzerindeki gerilim
100 V olduğundan, R direncinin üzerindeki gerilim
100 V olur. R direncinin üzerinden geçen akım 5A
olduğundan,
V 100
R= =
= 20X olur.
I
5
Evlerimizde kullandığımız hatların hepsi birbirine paralel bağlanmıştır.
Ütünün gücü 660W olduğundan üzerinden geçen akım,
›
=
CEVAP C
ε = 20 V
Σf
i=
ΣR
3.
R = 35Ω olur.
2Ω
1A
ε = 20 V
r=1Ω
2A
ε=240V
R direncin büyüklüğü,
CEVAP E
6Ω
Ι
VR = 140 V olur.
P = i2. R = 42 . 5 = 80 W olur.
4Ω
Vü=100V
240 = 100 + VR
5 Ω luk direncin gücü,
3A
VR
ε = Vü + VR
r
Ampermetre 2 A yi gösteriyorsa anakoldan geçen
akım, i = 4 A olur.
2.
R
ütü
R direncinin üzerindeki gerilim,
r
r
ε = 12 V
P=400W
I = 4A olur.
ε = 12 V
A
2A
Ütünün gücü 400W, gerilimi 100 V olduğundan
üzerinden geçen akım,
V
ε = 12 V
2A
4.
Elektrikli fırının gücü,
P = If.Vf
= 7.220
= 1540 W olur.
CEVAP B
III. yargı yanlıştır.
CEVAP C
106
ELEKTRİK VE MANYETİZMA
6.
Evlerimizde kullandığımız
hatların hepsi birbirine paralel bağlanmıştır.
Ι
Klimanın gücü 880 W olduğuna göre üzerinden geçen
akım,
Ι
1.
V
3Ω
Ι
ε =12V
K
Pk = Ik.Vk
Ι
880 = Ik.220
Ιk
Ik = 4A
Ιt
olur. Anakoldan geçen akım
It = 9 A olduğuna göre,
MODEL SORU - 7 DEKİ SORULARIN ÇÖZÜMLERİ
Ι
ε =12V
r=2Ω
klima
L
i
A
220V
r=2Ω
r=2Ω
ε =12V
2Ω
r=2Ω
M
ε =12V
r=2Ω
ε› =12V
It = Ik + 5I
9 = 4 + 5I
i=
5 = 5I
I = 1A olur.
Lambaların ikisi devreden çıkarıldığında paralel
bağlamada diğer aletlerin üzerindeki gerilim değişmeyeceğinden üzerlerinden geçen akımlar değişmez. Yeni durumda anakoldan geçen akım,
ε =12V
r› =1Ω
Σf
ΣR
›
=
f +f+f–f
5+1+2+2+2
=
12 + 12
12
= 2 A olur.
Ampermetre 2 amperi gösterir.
Iıt = Ik + 3I
3 Ω luk dirençten 2 dakikada yayılan enerji,
= 4 + 3.1
W = i2 . R . t
= 7A olur.
= 22 . 3 . 120
CEVAP C
= 4 . 360
= 1440 J olur.
CEVAP E
2.
K ve L anahtarları açık iken,
ε
i1 =
⇒ i1 = i olsun.
R
R direncinde harcanan enerji,
W1 = i2.R.t olur.
K ve L anahtarları kapalı iken, üreteçler paralel
bağlı olur. Toplam gerilim V2 =
ε olacağından,
ε
i2 =
= i olur.
R
R direncinde harcanan enerji,
W2 = i2.R.t olur.
Enerjilerin oranı ise,
W 1 i 2 .R.t
=
= 1 olur.
W 2 i 2 .R.t
CEVAP C
ELEKTRİK VE MANYETİZMA
107
3.
5.
Elektrik enerjisinin,
1 kWh i
0,5 ¨ ise
It =
E
30 ¨ olur.
–––––––––––––––––––––
E.(0,5) = 30 ⇒ E = 60 kWh olur.
4
E=Q
60 kWh enerji harcarsa
I2.R.t = 4.(m.c.ΔT)
1 günde
Eı enerji harcar.
––––––––––––––––––––––––––––
(20)2.8.t = 4.400.1.(100 – 40)
Eı.30 = 60.1 ⇒ Eı = 2 kWh olur.
800.t = 1600.60
1
dakika olur.
t = 30 s =
2
Klimanın gücü,
P=
f = 160 = 40A olur.
R efl
Suyun içerisindeki dirençten geçen akım bunun
yarısı olur. Su içerisindeki direnç ısınacağından
açığa çıkan enerji suyu kaynatmaya dönüşeceğinden,
Klimanın 30 günde harcadığı enerji 60 kWh olduğuna göre 1 günde harcadığı enerji,
30 günde
K anahtarı kapatıldığından anakoldan geçen akım,
›
E
2
1
=
= W olur.
t
10 5
CEVAP B
CEVAP A
6.
4.
1 aylık zaman içerisinde makinelerin harcadıkları
enerjileri ayrı ayrı bulalım:
Ütünün harcadığı enerji,
= 500.4
= 2kWh olur.
Tabletin harcadığı enerji,
Yıllık tüketilen enerji,
E2 = P2.t2 = 300.20 = 6 kWh tir.
E = 365.W
= 365.2
Televizyonun harcadığı enerji,
= 730 kWh olur.
E3 = P3.t3 = 300.10 = 3 kWh tir.
Radyonun harcadığı enerji,
1 kWh enerji 0,2 ¨ olduğundan,
E4 = P4.t4 = 200.5 = 1 kWh tir.
¨ = 730.0,2 = 146 ¨ olur.
CEVAP C
Toplam harcanan enerji,
Etoplam = E1 + E2 + E3 + E4
= 40 + 6 + 3 + 1
= 50 kWh olur.
1 kWh enerji 0,2 ¨ olduğundan, aylık elektrik faturası,
¨toplam = Etoplam.(0,2)
= 50.(0,2)
= 10 ¨ olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
W = P.t
= 2000 W.h
E1 = P1.t1 = 20.2000 = 40 kWh tir.
108
Makine günde 4 saat çalışıp gücü 500 watt olduğundan enerji tüketimi,
TEST
1
1.
ÇÖZÜMLER
4X
i1=3A
3.
3X
A
12X
i2=1A
ELEKTRİK DEVRELERİ
A1
i=4A
4X
r2=1X
ε1=50V
ε
R
A2
R
i1
ε2=10V
ε
ε
R
ε
ε
ε
i2
R
fiekil-Ι
R
r1=2X
fiekil-ΙΙ
R
i3
Ana koldan geçen akım;
ε1 – ε2
/ε
50 – 10 40
i=
=
=
=
= 4A
/ R 4 + 3 + r1 + r2 7 + 2 + 1 10
A3
ε
ε
olur. Şekilde görüldüğü gibi, ampermetre 3 amperi
gösterir.
fiekil-ΙΙΙ
CEVAP D
Şekil I deki devrede:
i1 =
3ε
olur.
2R
Şekil II deki devrede:
i2 =
2.
i
4X
i
ε
K
2ε
olur.
2R
Şekil III teki devrede:
i3 =
r=1X
ε
R
2
=
2ε
olur.
R
Buna göre,
V
i3 > i1 > i2 olur.
CEVAP C
K anahtarı kapalı iken:
Devreden geçen akım,
i=
V1 16
=
= 4A olur.
R
4
4.
4X
ε=12V
r=1X
Üretecin emk sı,
i=
A
/ε
ε
=
/R 4 + r
4=
ε
4 +1
ε = 20 V olur.
ε=12V
ε=12V
r=1X
r=1X
ε=12V
ε=12V
r=1X
r=1X
ε›=24V
r›=1X
Ampermetrenin gösterdiği değer,
K anahtarı açık iken:
i=
Voltmetrenin gösterdiği değer
V2 = ε = 20 V
CEVAP E
/ε
εı + ε
24 + 12 36
=
=
=
= 6A
/R
6
4 + rı + r 4 + 1+ 1
olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
109
5.
3R
7.
R
2R
R=5r
i
i
6R
16V
r
8V
ε1=12V
/ε =
r
ε
V
ε2=36V
ε
ε
ε
ε›=2ε
r
r
r›=r
ε
ε
r
r
ε2 – ε1 = 36 – 12 = 24 V
R direncinden geçen akım,
Şekilde görüldüğü gibi, voltmetre 8 voltu gösterir.
i=
CEVAP B
/ε
εı + ε – ε
2ε
2ε ε
=
=
=
=
/ R R + r ı + r + r 5r + r + r + r 8r 4r
olur.
CEVAP A
6.
R
R
R
R
A1
i1
8.
i2
ε
ε
A2
ε
R
ε
ε
A1
i1
ε
ε
ε
A3
A2
fiekil-ΙΙ
R
i
R
i2
R
fiekil-Ι
R
R
ε
ε
ε
fiekil-Ι
fiekil-ΙΙ
Şekil I deki devrede:
ε
i3
i1 =
ε+ε–ε
R
2
fiekil-ΙΙΙ
=
2ε
olur.
R
Şekil I deki devrede:
i1 =
Şekil II deki devrede:
ε
2ε
=
olur.
2R R
i2 =
Şekil II deki devrede:
i2 =
Buna göre,
4ε
2ε
olur.
=
R
R
2
2ε
i1
= R = 2 olur.
i2
ε
R
Şekil III teki devrede:
i akımı, i =
ε
R
2
=
i3 akımı ise i 3 =
2ε
olur.
R
i
ε olur.
=
2 R
Buna göre,
i2 > i1 = i3 olur.
CEVAP B
110
ELEKTRİK VE MANYETİZMA
ε + ε 2ε ε
olur.
=
=
R + R 2R r
CEVAP D
9.
11.
X
R
K
R
3X
2A
ε›=20V
ε=20V
1A
A
r=2X
ε
i1
›
r =1X
ε=20V
1A
r=2X
K ve L anahtarları açık iken:
X direncinin değeri,
i1 =
/ε
εı
i=
=
/ R x + 3 + rı
2=
ε
L
A
ε
olur.
R
K anahtarı kapalı iken:
20
x + 3+1
R direncinden geçen akım;
ε 2ε
i2 =
=
olur.
R
R
2
x + 4 = 10
x = 6 X olur.
CEVAP C
K ve L anahtarları kapalı iken:
R direncinden geçen akım;
10.
i3 =
3X
i
r=2X
i
2
r=2X
ε=24V
K
i
2
r=2X
=
2ε
R
Buna göre, i2 = i3 > i1 olur.
ε=24V
ε=24V
ε
R
2
12.
R
ε›=24V
R
R
R
r›=1X
L
CEVAP E
R
R
ε
ε
i1
ε
ε
i2
ε
Ana koldan geçen akım,
i=
/ε
εı + ε
24 + 24 48
=
=
=
= 8A
/R
3 + rl + r 3 + 1 + 2
6
VKL = / ε – / Ri
= –24 +
fiekil-ΙΙ
Şekil Ι deki devrede:
Devreden geçen akım,
3ε
ε
olur.
i1 =
=
3R R
olur. VKL potansiyel farkı,
= –ε +
fiekil-Ι
i
.r
2
Üreteçlerin tükenme süresi,
qR
ε
q = .t1 ⇒ t1 =
olur.
ε
R
8
.2
2
Şekil ΙΙ deki devrede:
= –16 V olur.
CEVAP A
Ana koldan geçen akım;
3ε
2ε
i2 =
=
olur.
R
2R
3
Üreteçlerin tükenme süresi;
qR
3ε
q=
.t ⇒ t2 =
olur.
3ε
R 2
Buna göre;
qR
t1
= ε = 3 olur.
t2
qR
3f
CEVAP E
ELEKTRİK VE MANYETİZMA
111
TEST
1.
2
Şekil-I deki devrede:
i1 =
/ε
/R
2=
2ε
20 + 2r
3=
7+
R
ε
A2
olur.
r
ε1
A1
ε
R
i2
i1
ε1
ε2
ε1
ε2
ε2
r
fiekil-Ι
/ε
/R
ε
R
A1
Şekil-II deki devrede:
3=
R
3.
20X
R
ε = 20 + 2r
i2 =
ELEKTRİK DEVRELERİ
ÇÖZÜMLER
fiekil-Ι
7X
fiekil-ΙΙ
Şekil-I deki devrede:
A2
r
2
i1 =
ε
20 + 2r
r
7+
2
/ε
=
/R
ε1 + ε1 + ε1
R
2
r
1
r=1
2
r
3
r
2
6ε 1
R
olur.
Şekil-II deki devrede:
ε
20 + 2r = 21 +
=
i2 =
fiekil-ΙΙ
ε2 + ε2
3R
2
=
4ε 2
3R
olur.
i1 ve i2 taraf tarafa oranlanırsa,
ε nin değeri ise, r = 2 Ω olur.
ε = 20 + 2.2
ε = 24 olur.
2.
i1
i2
R
K
R
4ε 2
3 18ε 1
=
&
2
4ε 2
2R
i1
=
3R
CEVAP E
V
i1
6ε 1
2R
ε
2R
ε
4.
ε1 1
=
olur.
ε2 3
ε
R=3r
K
CEVAP A
L
r
r
K anahtarı açık iken:
ε
Devreden geçen akım,
i1 =
/ε
ε
=
olur.
/R
5R
Voltmetrenin gösterdiği değer,
V1 = i1.2R =
ε
5R
.2R =
ε
5R
olur.
i=
Ana koldan geçen akım;
.2R =
f
112
ELEKTRİK VE MANYETİZMA
r
ε
r
r
/ε
εı – ε + ε
εı
2ε
ε
=
=
=
=
ı
/R
5
r
+ r 6r 3r
3r + r + r + r
= – ε – 4r.i
2
= – ε – 4r.
olur.
Buna göre,
2ε
V1
4
= 5 =
olur.
V2
ε
5
2
r›=r
r
ε
VKL = / ε – / Ri
Voltmetrenin gösterdiği değer,
4R
ε›=2ε
olur. VKL potansiyel farkı,
/ε
ε
i2 =
=
olur.
/R
4R
V2 = i2.2R =
ε
Devreden geçen akım,
K anahtarı kapalı iken:
ε
ε
= –ε –
= –
CEVAP C
ε
3r
4ε
3
7ε
olur.
3
CEVAP D
5.
i
2
7.
ε›=ε
ε
r
R
r›= r
2
R
A1
R
ε
fiekil-ΙΙ
fiekil-Ι
R
R
R direncinden geçen akım,
i=
/ε
ε
=
=
/R
R + rı
ε
R+
ε2
i2
r
ı
A2
ε1
i1
i
2
R
R
R
i
R
A3
olur.
r
2
ε3
i3
CEVAP A
fiekil-ΙΙΙ
Şekil I deki devrede:
i1 =
ε1
3R
olur.
Şekil II deki devrede:
ε2
i2 =
2ε 2
=
3
R
2
olur.
3R
Şekil III teki devrede:
6.
R1=4r
R2=3r
R
2
A2
A1
i1
ε3
i3 =
i2
ε
2r
2r
fiekil-Ι
2ε 3
R
olur.
Buna göre,
i1 = i2 = i3
ε
ε
=
2r
ε1
ε
3R
2r
=
2ε 2
3R
=
2ε 3
R
ε1 > ε2 > ε3 olur.
fiekil-ΙΙ
Şekil-I deki devrede:
i1 =
5X
8.
Ampermetrenin gösterdiği değer,
/ε
ε+ε
2ε
ε
olur.
=
=
=
/R
4r + 2r + 2r 8r
4r
i
Şekil-II deki devrede:
Ampermetrenin gösterdiği değer;
i2 =
CEVAP E
ε
ε
r=1X
r=1X
/ε
εı
ε
ε
olur.
=
=
=
/R
3r + r ı 3r + r 4r
i
ε
r=1X
V
Devreden geçen akım,
Buna göre,
i=
ε
i1
= 4r = 1 olur.
i2
ε
4r
V 30
=
= 6A
5
R
olur.
CEVAP C
ε un değeri,
V = 3ε –i.3r
30 = 3ε – 6.3.1
30 = 3ε – 18
3ε = 48
ε = 16 V olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
113
9.
3X
11.
3X
ε=18V
i
K
L
r=2X
5A
1A
ε1
ε2
r1=2X
ε2
ε1
r2=1X
i
5X
r1=2X
r2=1X
r›=1X
r=2X
ε=18V
Şekil-I deki devrede:
ε=18V
r=2X
/ε
/R
r=2X
fiekil-Ι
i1 =
i1 =
5=
fiekil-ΙΙ
Devreden geçen akım,
ε1 + ε2
i=
3 + r1 + r2
ε1 + ε2
⇒ ε1 +
3+ 2+1
i2 =
1=
/ε
ε + εı + ε – ε
18 + 18
=
=
= 3A
/R
5 + r + r ı + r + r 5 + 2 + 1+ 2 + 2
olur. VKL potansiyel farkı,
ε2 = 30 V olur.
VKL = / ε – / Ri
Şekil-II deki devrede:
i2 =
=
/ε
/R
3 + r1 + r2
3+ 2+1
ε – r.i
= 18 – 2.3
= 18 – 6
= +12 V olur.
ε1 – ε2
ε1 – ε2
⇒
CEVAP B
ε1 – ε2 = 6 V olur.
12.
Buna göre,
ε1 + ε2 = 30
+ ε1 – ε2 = 6
R
R
R
R
i1
2ε1 = 36
i2
ε
ε
ε
ε
ε1 ve ε2 taraf tarafa oranlanırsa,
ε 1 18 3
=
= olur.
ε 2 12 2
εK
fiekil-Ι
CEVAP A
εL
K
L
εM
i1 =
ε–ε+ε
2R
=
ε
2R
ε
2R
.4 = 2ε olur.
Şekil ΙΙ deki devrede:
N
P
Ana koldan geçen akım;
εM = εN + εP dır.
ΙΙ. yargı kesinlikle doğrudur.
εN ile εP yi karşılaştıramayız.
ΙΙΙ. yargı için kesin birşey söylenemez.
CEVAP D
ELEKTRİK VE MANYETİZMA
olur.
Üreteçlerin yükü,
εP
Buna göre,
• εL > εK dır.
Ι. yargı kesinlikle doğrudur.
114
Devreden geçen akım,
εN
Üreteçlerin hiçbirinden akım geçmediğine göre,
εL – εK = εM = εN + εP dir.
•
fiekil-ΙΙ
Şekil Ι deki devrede:
q = i1.t1 =
M
•
ε
ε
ε1 = 18 V
ε2 = 12 V olur.
10.
ε=18V
r=2X
ε=18V
ε›=18V
i2 =
ε
R
2
=
2ε
olur.
R
Üreteçlerden geçen akım;
iı2 =
2ε
olur.
3R
Üreteçlerin tükenme süresi;
q = iı2.t2
2ε =
2ε
.t
3R 2
t2 = 3 saat olur.
CEVAP B
TEST
3
ÇÖZÜMLER
1.
3.
3Ω
2Ω
ENERJİ, GÜÇ VE KIRCCHOFF KURALLARI
Ütünün üzerindeki gerilim 120 volt olacağından
P = V.Ι
6Ω
A
3Ω
ε2 = 12 V
r2 = 2Ω
ε3 = 12 V
120V
R
1200 = 120.Ι
ε = 12 V
r = 2Ω
i
ütü
üzerindeki akım,
+ –
Ι = 10 A olur.
i
240V
Kaynak 240V olduğundanbunun 120 voltu ütü
ε› = 12 V
r› = 1Ω
üzerinde ise direncin gerilimi,
VR = 240 – 120 = 120V olur.
r3 = 2Ω
Devreden geçen akım Ι = 10A olduğuna göre, R
i=
f+f
›
direnci,
3+2+r+r
›
=
12 + 12
3+2+1+1
=
24
8
R=
V 120
=
= 12 X olur.
I
10
CEVAP B
= 3 A olur.
4.
Ampermetre 1 amperi gösterir.
2
Lambalar 30 günde 12 ¨ enerji tüketiyorsa 1 günde
tüketilen enerji miktarı,
2
P = i 2 . R = 1 . 6 = 6 W olur.
CEVAP D
30 günde
12 ¨ ise
1 günde
T dir.
______________________
30.T = 1.12 ⇒ T = 0,4 ¨ olur.
1 kWh enerjinin ¨ olarak değeri 0,2 ¨ olduğuna
2.
3Ω
2A
göre tüketilen enerji miktarı,
2Ω
3Ω
1 kWh i
6Ω
1A
r = 2Ω
A
ε = 10V
ε2 = 10 V
ε2 = 10 V
3A
r2 = 2Ω
i=
Bu enerji 5 tane lamba için geçerlidir. 1 lambanın
ε3 = 10 V
günlük tükettiği enerji,
ε› = 10 V
r› = 1Ω
5 lamba
Σf
ΣR
2 kWh tüketirse
1 lamba
E1 tüketir.
___________________________
›
=
f +f+f
3+2+2+2+1
=
30
10
E1.5 = 1.2 ⇒ E1 = 0,4 kWh olur.
Lambalar günde 10 saat çalıştığına göre bir lambanın gücü,
=3A
P=
Ampermetre 2 amperi gösterir.
2
E
0,4 ¨ olur.
________________________
E.(0,2) = 1.(0,4) ⇒ E = 2 kWh olur.
r2 = 2Ω
r3 = 2Ω
0,2 ¨ ise
E 1 0, 4 kWh
=
= 0, 04 kW = 40 watt
t
10h
olur.
2
P = i 2 . R = 1 . 6 = 6 W olur.
CEVAP E
CEVAP B
ELEKTRİK VE MANYETİZMA
115
5.
1 aylık zaman içerisinde makinelerin harcadıkları
enerjileri ayrı ayrı bulalım:
7.
K lambasının üzerinden geçen akım,
PK = ΙK.VK
Ütünün harcadığı enerji,
60 = ΙK.120
E1 = P1.t1 = 1500.20 = 30 kWh tir.
ΙK = 0,5A
Süpürgenin harcadığı enerji,
L lambasının üzerinden geçen akım,
E2 = P2.t2 = 2000.10 = 20 kWh tir.
PL = ΙL.VL
Televizyonun harcadığı enerji,
120 = ΙL.120
E3 = P3.t3 = 50.200 = 10 kWh tir.
ΙL = 1A
M lambasının üzerinden geçen akım,
Toplam harcanan enerji,
Etoplam = E1 + E2 + E3
PM = ΙM.VM
= 30 + 20 + 10
180 = ΙM.120
= 60 kWh olur.
ΙM = 1,5A olur.
1 kWh enerji 0,2 ¨ olduğundan, aylık elektrik faturası,
Pil üzerinden çekilen akım,
Ι = ΙK + ΙL + ΙM
¨toplam = Etoplam.(0,2)
= 0,5 + 1 + 1,5
= 60.(0,2)
= 3A olur.
= 12 ¨ olur.
CEVAP C
CEVAP E
8.
6.
ε=20V
2Ω
+ –
Ι
6Ω
K
K
6Ω
6Ω
L
RKL=2Ω
3Ω
6Ω
K
6Ω
K
›
Pf = If.Vf
A
880 = If.220
L
f›r›n
Ιf
Ιf
Fırının gücü P = 880W
olduğundan üzerinden
geçen akım,
r=1Ω
2Ω
Evlerimizde kullandığımız hatların hepsi birbirine paralel bağlanmıştır.
Ιü
f›r›n
ütü
Ι
V=220V
If = 4A olur.
Devrenin eşdeğer direnci,
Anakol akımı 6 A olduğundan ütünün üzerinden
geçen akım,
Reş = 2 + 1 + 2 + 2 + 3 = 10Ω olur.
I = If + Iü
Devreden geçen I akımı,
I=
6 = 4 + Iü
20
f
=
= 2A olur.
R efl 10
Iü = 2A olur.
Aynı fırından bir tane daha bağlandığında devreden geçen anakol akımı,
Üretecin verimi,
h=
f – I.r 20 – 2.1
=
= 0, 9
f
20
Iı = Iü + If + Ifı
=2+4+4
% verim = η.100 = 0,9.100 = 90 olur.
= 10A olur.
CEVAP D
116
ELEKTRİK VE MANYETİZMA
CEVAP C
9.
Şekildeki devrede
4R ile 12 R direnci
birbirlerine paralel,
bunlar da 3R
direncine sesi
bağlıdır.
R
2Ι
2R
11.
3Ω
Ι
Refl=3R
3R
2Ω
Ι.ilmek
Ι1
ΙΙ.ilmek
+ –
3Ω
55V
Ι. ilmek için K.G.Y yazacak olursak,
4R.12R
= 3R
4R + 12R
55 – 2Ι1 – 3Ι1 – 5(Ι1 + Ι2) – 10 = 0
40 – 2Ι2 – 5(Ι1 + Ι2)– 3Ι2 – 10 = 0
E2 = I2.3R.t =3I2R.t
10Ι2 + 5Ι1 = 30 .. .(
olur. E1 ve E2 taraf tarafa oranlarırsa,
E 1 4I2 .R.t 4
olur.
=
=
E 2 3I2 .R.t 3
ε1=10V
CEVAP D
(–2).10Ι1 + 5Ι2 = 45.(–2)
10Ι2 + 5Ι1 = 30.(1)
+ ___________________
–20Ι1 – 5Ι1 = –60
–15Ι1 = –60
–
+ ε2=6V
2Ω
Ι.ilmek
Ι1 = 4A olur.
ΙΙ.ilmek
Ι3
4Ω
' ve ( denklemlerini ortak çözersek,
Ι2
+ –
Ι1
10Ι1 + 5Ι2 = 45...'
ΙΙ. ilmek için K.G.Y yazılırsa,
E1 = (2I)2.R.t =4I2 R.t
Ι1
+
– 40V
+
– 10V
olur. Üst koldan 2I akımı geçerse alt koldan I akımı
geçer. R ve 3R dirençlerinden yayılan enerji,
10.
Ι2
5Ω
3Ι
4R ile 12R direncinin eşdeğeri,
R efl =
2Ω
4A lik akımı, 4Ω luk dirençlere eşit paylaşırlar.
Ι2
4 Ω luk direnin gücü,
I. yol: Ι. ilmek için K.G.Y yazılırsa,
P = 22.4
Σε – ΣΙ.R = 0
= 16 watt olur.
10 – (4.Ι1 + 2.(Ι1 + Ι2)) = 0
CEVAP A
3Ι1 + Ι2 = 5 ... '
ΙΙ. ilmek için K.G.Y yazılırsa,
Σε – ΣΙ.R = 0
6 – 2.(Ι1 + Ι2) = 0
12. K anahtarı kapatıldığında ana koldan geçen akım,
Ι1 + Ι2 = 3 ... (
' ve ( denklemleri çözülecek olursa,
3Ι1 + Ι2 = 5
I=
(–3).Ι1 + Ι2 = 3.(–3)
+ ___________________
– 3Ι1 – 3Ι2 = – 9
+ ___________________
2Ι2 = 4 ⇒ Ι2 = 2A olur.
I2 akımı ( nolu denklemde yerine yazılırsa,
Ι1 + 2 = 3 ⇒ Ι1 = 1A olur.
K
3Ω
2
su
Ιt=15A
ε=30V
r=0
Bu direnç ısınacağından açığa çıkan enerji, suyu
kaynatmaya dönüşeceğinden,
E=Q
2Ω luk direncin üzerinden geçen akım,
I2.R.t = 4.(m.c.ΔT)
Ι3 = Ι1 + Ι2 =1 + 2 = 3A olur.
(10)2.3.t = 4.300.1.(100 – 40)
II. yol: II. ilmek için KGY yazılırsa,
300.t = 4.300.60
ΣRΙ = Σε
2.I3 = 6 ⇒ I3 = 3 A olur.
6Ω
10A
f = 30 = 15A
R efl
olur. Bu akım ik ye
ayrıldığında 3 X luk dirençten 10 A lik akım
geçer.
3Ι1 + Ι2 = 5
5A
t = 240 s = 4 dakika olur.
CEVAP E
CEVAP A
ELEKTRİK VE MANYETİZMA
117
13.
ε1=28V
ε2=20V
+ –
– +
14.
Ι2
ε=50V Ι
+ –
Ι
2Ω
2Ω
K
r=2Ω
k›sa
devre
3Ω
Ι1
Ι.ilmek
+ ε =5V
– 1
4Ω
5Ω
ΙΙ.ilmek
10Ω
Ι
8Ω
ε=50V
– +
r=2Ω
Ι. ilmek için K.G.Y uygulanırsa,
9Ι1 + 3Ι2 = 33 ... '
ΙΙ. ilmek için K.G.Y uygulanırsa,
20 – 5Ι2 + 5 – 3.(Ι1 + Ι2) = 0
8Ι2 + 3Ι1 = 25 ... (
6Ω
K
Ι
Ι
K
I=
f+f
R efl
=
50 + 50
2 + 10 + 2 + 6
=
100
20
= 5A olur.
' ve ( denklemlerini ortak çözersek,
Pilin verimi,
9Ι1 + 3Ι2 = 33
h=
(–3).8Ι2 + 3Ι1 = 25.(–3)
+ _____________________
f – I.r 50 – 5.2
=
= 0, 8
f
50
% verim = η.100
–24Ι2 + 3Ι2 = –75 + 33
= 0,8.100
21Ι2 = 42
= 80
Ι2 = 2A olur.
CEVAP D
5Ω luk direncin gücü ise,
P = Ι2.R = (2)2.5 = 20 watt olur.
CEVAP E
ELEKTRİK VE MANYETİZMA
Ι
6Ω
A
Devreden geçen Ι akımı,
28 – 2Ι1 – 4Ι1 + 5 – 3.(Ι1 + Ι2) = 0
118
k›sa
devre
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
1.
i1
ε
ε
R
ε
Bölüm
Yazılı Soruları
(Elektrik Devreleri)
A1
A2
R
b)
ε
R
R
ε
fiekil- I
24 – 8 + f3
8+2+1+1
36 = 24 – 8 + f3
fiekil- II
R
36 = 16 + f3
R/2
f3 = 20 V olur.
R
A3
ε
i3
Σf
ΣR
f1 – f2 + f3
i=
5 + 3 + r1 + r2 + r3
i=
3=
ε
i2
ÇÖZÜMLER
ε
ε
c) VKL = Σε – ΣR . i
fiekil- III
= – ε2 – (1 + 3) . i
f+f–f
f
i1 =
=
2R
2R
f + f 2f
f
i2 =
=
=
2R
2R R
2f
f+f–f
f
i3 =
=
=
R
R
R
2
2
=–8–4.3
= – 20 V olur.
d)
Verim =
i3 > i2 > i1 olur.
f3 – i.r3
f3
20 – 3.1
20
17
=
20
17
% Verim =
.100 = 85 olur.
20
=
2.
ε2 = 8 V
K
i
3Ω
L
3.
r2 = 1Ω
R /2
R
R
r3 = 1Ω
A
5Ω
R
i
ε1 = 24 V
r1 = 2Ω
ε3
R
A2
R
A1
i1
ε
ε
i2
R
ε
ε
ε
V
ε
a) V =
ε1 – i . (5 + r1)
fiekil- I
fiekil- II
= 24 – 3 . (5 + 2)
=3V
Voltmetre 3 voltu gösterir.
3f
3
R
i1
= 2 = 1 olur.
i2
2f
R
ELEKTRİK VE MANYETİZMA
119
4.
4Ω
K
i
ε1 = 24 V
5.
L
r1 = 2Ω
ε2 =10V
r2 = 1Ω
A
3Ω
3Ω
1A
6Ω
i
A
ε =10V
r=1Ω
RX
4Ω
2Ω
3A
T
N
2A
ε =10V
ε =10V
M
a) i = Σf
ΣR
r=1Ω
r=1Ω
ε =10V
ε =10V
r=1Ω
r=1Ω
ε› =20V
r› =1Ω
V
f1 – f2
=
4+4+3+2+1
24 – 10
=
14
14
=
14
= 1 A olur.
3 Ω luk dirençten 10 saniyede yayılan enerji,
W = i 12 . R . t
= 22 . 3 . 10
= 120 J olur.
b) VKL = Σε – ΣR . i
=
ε1 – i . (4 + 2)
= 24 – 1 . 6
6.
ε=215V
Ι
+ –
Ι
= 18 V olur.
R
5Ω
V
Ι
c)
VTN = Σε – ΣR . i
VTN = 0 – 3 . 1
VN – VT = –3
VN – 0 = –3
VN = – 3 V olur.
VMT = Σε – ΣR . i
VMT = 0 – 4 . 1
VT – VM = – 4
0 – VM = – 4
VM = +4 V olur.
V = I.R
15 = I.5 ⇒ I = 3A olur.
K lambasının gücü 540 watt olduğuna göre,
P = I2.RK
540 = (3)2.RK ⇒ RK = 60Ω olur.
I=
f
R efl
3=
215
20
&R=
X olur.
5 + 60 + R
3
R direncinin gücü,
2
Verim =
f2 – i.r2
f2
10 – 1.1
10
9
=
= 0, 9
10
%Verim = 0, 9.100 = 90 olur.
=
120
ELEKTRİK VE MANYETİZMA
Ι
RK
2
P = I .R = (3) .
d)
K
20
= 60 watt olur.
3
7.
9.
V
ε =12 V
i
i2
ε
ε
r=2Ω
r=2Ω
›
i2
r=2Ω
fiekil- II
Şekil-I
deki devrede:
_________________
›
i1 =
2f
2f
2f f
=
=
=
R 1 + r + r 6 + 2 + 2 10 5
q = i 1 .t 1
b) VKL = Σε – ΣR . i
=ε–7.i
= 12 – 7 . 2
=–2V
Voltmetre 2 voltu gösterir.
Şekil-II
deki devrede:
_________________
f
f
f
i2 =
=
=
›
4+1 5
R +r
2
Üreteçlerden geçen akım,
i2
c) P = . R
= 22 . 5
= 20 W olur.
K
ε
fiekil- I
f +f+f–f
5+2+2+2+1
24
=
12
= 2 A olur.
a) i =
›
i2
r=2Ω
r = 2Ω
r = 2Ω
r› = 1 Ω
8.
ε
i
ε = 12 V
r = 2Ω
ε =12 V
ε
i1
ε = 12 V
r = 2Ω
ε =12 V
› = 12 V
R2 =4Ω
5Ω
r = 2Ω
A
R1 =6Ω
ı
q = i2 . t2
ı
i1 . t1 = i2 . t2
ε2 = 10 V
i
3Ω
f
f
.8=
.t
5
10 2
L
t2 = 16 saat olur.
r2 = 1Ω
3Ω
A
ε1 = 20 V
i
2Ω
r1 = 1Ω
V
ε2
10.
a) i = Σf
ΣR
f1 + f2
=
3 + 3 + 2 + r1 + r2
20 + 10
8+1+1
30
=
10
=3A
2Ω
4Ω
I. ‹LMEK
b) V = ε1 – i . (r1 + 2)
= 20 – 3 . (1 + 2)
= 20 – 9
= 11 V
Voltmetre 11 voltu gösterir.
c) VKL = Σε – ΣR . i
= ε2 – (3 + 1) . 3
= 10 – 12
= – 2 V olur.
2Ω
i3 =1A
=
Ampermetre 3 amperi gösterir.
II. ‹LMEK
ε1
i1 =4A
i2 =3A
i1 = i2 + i3
i1 = 3 + 1 = 4 A
I. ilmek için:
_____________
II. ilmek için:
_____________
Σε = ΣR . i
Σε = ΣR . i
ε1 = i1 . 2 + i3 . 4
ε2 = i2 . 2 – i3 . 4
ε1 = 4 . 2 + 1 . 4
ε2 = 3 . 2 – 1 . 4
ε1 = 12 V olur.
ε2 = 2 V olur.
f1 12
=
= 6 olur.
2
f2
ELEKTRİK VE MANYETİZMA
121
